《算法笔记》总结No.5——递归

一.分而治之
将原问题划分为若干个规模较小而结构与原问题相同或相似的子问题,然后分别解决这些子问题,最后合并子问题的解,即可得到原问题的解,步骤抽象如下:
- 分解:将原问题分解为若干子问题
- 解决:递归求解所有子问题,如果子问题的规模小到可以直接解决,就直接解决它
- 合并:将子问题的解合并为原问题的解
子问题之间应该是相互独立且没有交叉的,从严格的定义上将,子问题个数为1的情况称为减治,而大于1的情况称为分治。
分治法作为一种思想,即可使用递归的手段去实现,也可以通过非递归的手段去实现。
二.递归
递归的一个很符合精髓且搞笑的定义:要理解递归,你要先理解递归,直到你能理解递归为止。
递归的核心在于——反复调用自身函数,但是每次能把问题范围缩小,直到范围缩小到可以直接得到边界数据的结果,然后再在返回的路上求出对应的解。
两个重要概念:
- 递归边界:分解问题的尽头
- 递归式(或者称之为递归调用、递归函数):分解子问题的手段
如果使用递归而式而不进行阻止,那么最后将会无法停止这个黑洞似的无穷尽的算法。递归的代码结构中移动存在上述两个概念,他们支撑起了整个递归最关键的逻辑。
三.递归计算阶乘
直接先上代码:
#include <iostream>
using namespace std;int F(int n){if(n==0) return 1;elsereturn F(n-1)*n;
}int main() {int n=0;cin>>n;cout<<F(n);return 0;
}仔细观察,不难发现:
- 递归边界:n==0
- 递归式:F(n-1)*n
来仔细的分析一下,对于F(5)来说——相当于是F(4)*5,以此类推,直接将F(5)分解到了F(0),此时F(0)=1,即子问题的答案,再将所有子问题的答案合并,即可完成本次求解~

假设输入的是3,则推倒过程依次为:
- F(3)
- F(2)*3
- F(1)*2*3
- F(0)*1*2*3
- 得到最后的F(0)的值以后,再返回去依次计算F(1)、F(2)、F(3)
四.递归计算裴波那契数列
#include <iostream>
using namespace std;int F(int n){if(n==0||n==1) return 1;elsereturn F(n-1)+F(n-2);
}int main() {int n=0;cin>>n;cout<<F(n);return 0;
}仔细观察,也没什么难度:
- 递归边界:0和1的返回值均为1
- 递归式:根据定义,第三项开始即为前两项的和
对于这类递归问题,只要找到了递归边界和递归式,写起来代码就没什么难度。递归边界用来返回最简单底层的结果,递归式用来减小规模并进一步向下一层递归。递归图可以将递归放在一个平面上思考,有利于更快分析题目~

五.全排列
某种意义上来说,学会递归的思维正是从一个只会暴力的小白蜕变的过程,比如当我们要求输入1~n之间数的全排列,如果硬碰硬直接霸王硬上弓,这个复杂度简直不能想象——毕竟光数量都达到n的阶乘个,何况找起来也是很费事的。
从递归的角度去考虑,如果把问题描述成“1~n这n个整数的全排列”,那么就可以拆分为若干个子问题:“输出以1开头的全排列”、“输出以2开头的全排列”……以此类推。不妨设置一个数组P,用来存放当前的排列;再设置一个散列数组hashTable,其中hashTable[x]当x已在P中时赋值为true。
现在按照顺序往P中的第1位到第N位填入数字。不妨假设当前已经填好了1~index-1位,正准备去填写index位。我们需要枚举1~n,如果当前枚举的数字x还没哟再1~index-1中,即填入到index位,同时设置hashTable[x]为true,然后去处理index+1位;如果递归完成时,以便让P[index]填写下一个数字。
#include <cstdio>
#include <iostream>
using namespace std;
const int maxn=11;int n,P[11],hashTable[maxn]={false};
//p为当前排列
//hashTable用来记录x是否已经在P中! void generateP(int index) //当前处理的正是第index位
{if(index==n+1) //1~n已经处理完了,所以相当于n+1为递归边界~ {for(int i=1;i<=n;i++)cout<<P[i]; //输出当前排列 cout<<endl;return;}for(int x=1;x<=n;x++) //枚举1~n,试图将x填入到P[index]位上! {if(hashTable[x]==false) //false即表示不存在~ {P[index]=x; //填入到index位 hashTable[x]=true; generateP(index+1); //递归处理下一位:即index+1 hashTable[x]=false;}}
}int main() {n=3;generateP(1);return 0;
}- 递归边界:index==n+1
- 递归式:generateP(index+1);
六.N皇后问题
N 皇后问题指的是如何将 N 个皇后放置在 N × N 的棋盘上,并且使皇后彼此之间不能相互攻击。即给你一个整数 N ,返回所有不同的 N 皇后问题的解决方案数量~

这玩意,不知道大家有没有想起来行列式的定义:将行列式视为从矩阵的不同行和不同列中选取元素并相乘的代数和。每一项的符号由列标的逆序数决定,即如果列标的逆序数为奇数,则该项为负;若为偶数,则该项为正——其实就是全排列~不过不同的是,行列式可以在对角线上选择元素,而对于可以斜线行走的皇后,这一点显然也是不行。因此可以基于全排列的代码,然后对每一个全排列的结果进行单独判断是否存在对角线元素,即可完成~

如下:判断是否在同一对角线,只需要看行距之差和列距之差的绝对值是否相同,即可:
int count=0;
void generateP(int index) //当前处理的正是第index位
{if(index==n+1) //1~n已经处理完了,所以相当于n+1为递归边界~ {bool flag=true; //flag为true时表示当前为一个合法方案~ for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)if(abs(i-j)==abs(P[i]-P[j])) flag=false; //不合法 }if(flag)count++;return;}for(int x=1;x<=n;x++) //枚举1~n,试图将x填入到P[index]位上! {if(hashTable[x]==false) //false即表示不存在~ {P[index]=x; //填入到index位 hashTable[x]=true; generateP(index+1); //递归处理下一位:即index+1 hashTable[x]=false;}}
}对于递归,只要想清楚边界、递归式、问题需要的答案,就没什么难度~
相关文章:

《算法笔记》总结No.5——递归
一.分而治之 将原问题划分为若干个规模较小而结构与原问题相同或相似的子问题,然后分别解决这些子问题,最后合并子问题的解,即可得到原问题的解,步骤抽象如下: 分解:将原问题分解为若干子问题解决&#x…...

鸿蒙小练习
bean对象 export class BannerImage{id:numberurl:stringtargetUrl:stringproductId:numberconstructor(id: number, url: string, targetUrl: string, productId: number) {this.id idthis.url urlthis.targetUrl targetUrlthis.productId productId} }export class d…...

谷粒商城-个人笔记(集群部署篇二)
前言 学习视频:Java项目《谷粒商城》架构师级Java项目实战,对标阿里P6-P7,全网最强学习文档: 谷粒商城-个人笔记(基础篇一)谷粒商城-个人笔记(基础篇二)谷粒商城-个人笔记(基础篇三)谷粒商城-个人笔记(高级篇一)谷粒商城-个…...

Python面试题-7
21. 请解释Python中的元组。 Python中的元组(Tuple)是一种内置的数据结构,它有如下特点: 有序性:元组中的元素是有序的,每个元素都有一个索引,索引从0开始。不可变性:一旦元组被创…...

微信⼩程序的电影推荐系统-计算机毕业设计源码76756
摘 要 随着互联网的普及和移动互联网的发展,人们对于获取信息的便捷性和高效性要求越来越高。电影作为一种受众广泛喜爱的娱乐方式,电影推荐系统的出现为用户提供了更加个性化和精准的电影推荐服务。微信小程序作为一种轻量级应用形式,在用…...

理解与解读李彦宏在2024世界人工智能大会的发言:应用优先于技术
2024年7月4日,世界人工智能大会暨人工智能全球治理高级别会议在上海世博中心举行。百度创始人、董事长兼首席执行官李彦宏在产业发展主论坛上提出了一个引人深思的观点:“大家不要卷模型,要卷应用!”他强调了一个重要的观点&#…...

数字化打破传统,引领企业跨界经营与行业生态盈利
在当今数字化时代,传统的赚货差思路正面临着巨大的挑战。然而,数字化的崛起为企业提供了突破传统束缚的机会,促使其转向跨界经营,并通过行业生态经营获取利润。 首先,数字化打破了传统赚货差思路的局限性。以往&…...

【链表】- 链表相交
1. 对应力扣题目连接 链表相交 2. 实现思路 链表详情: 考虑使用双指针: 解法一: 具体代码,详见3. 实现案例代码解析: 思路:因为链表按照如图的箭头走向,走的总路程是相等的,一…...

【python 学习】快速了解python内置类型
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《C干货基地》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! 文章目录 前言一、内置类型的介绍1.1 类型体系1.2 空类型和None1.3 布尔值 二、内置类型的运算2.1 布尔运算2.2 比较运算符比较…...

npm ERR! code ENOTEMPTY npm ERR! syscall rename npm ERR!
报错: npm ERR! code ENOTEMPTY npm ERR! syscall rename npm ERR! path /home/user/.local/lib/node_modules/pkg npm ERR! dest /home/user/.local/lib/node_modules/.pkg-piikcue3 npm ERR! errno -39 npm ERR! ENOTEMPTY: directory not empty, rename ‘/home/…...

智能井盖采集装置 开启井下安全新篇章
在现代城市的脉络之下,错综复杂的管网系统如同城市的血管,默默支撑着日常生活的有序进行。而管网的监测设备大多都安装在井下,如何给设备供电一直是一个难题,选用市电供电需经过多方审批,选用电池供电需要更换电池包&a…...

C# AGV小车通讯开发的方法
AGV (Automated Guided Vehicle) 小车的通讯开发通常涉及与AGV控制系统或调度系统的数据交换。在C#中实现AGV小车通讯,可以采用多种方法,具体取决于AGV的通信协议和硬件接口。以下是一些常用的开发方法: 1. 串行通讯 (Serial Communication)…...
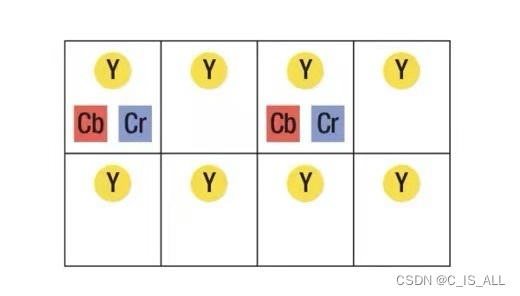
01-图像基础-颜色空间
1.RGB颜色空间 RGB是一种常用的颜色空间,比如一幅720P的图像,所对应的像素点个数是1280*720,每一个像素点由三个分量构成,分别是R,G,B。 R代表红色分量,G代表绿色分量,B代表蓝色分量,以24位色来…...

双向链表+Map实现LRU
LRU: LRU是Least Recently Used的缩写,即最近最少使用,是一种常用的页面置换算法,选择最近最久未使用的页面予以淘汰。 核心思想: 基于Map实现k-v存储,双向链表中使用一个虚拟头部和虚拟尾部,虚拟头部的…...

HTML(27)——渐变
渐变是多个颜色逐渐变化的效果,一般用于设置盒子模型 线性渐变 属性:background-image : linear-gradient( 渐变方向 颜色1 终点位置, 颜色2 终点位置, ......); 取值: 渐变方向:可选 to 方位名词角度度数 终点位置:可选 百分…...
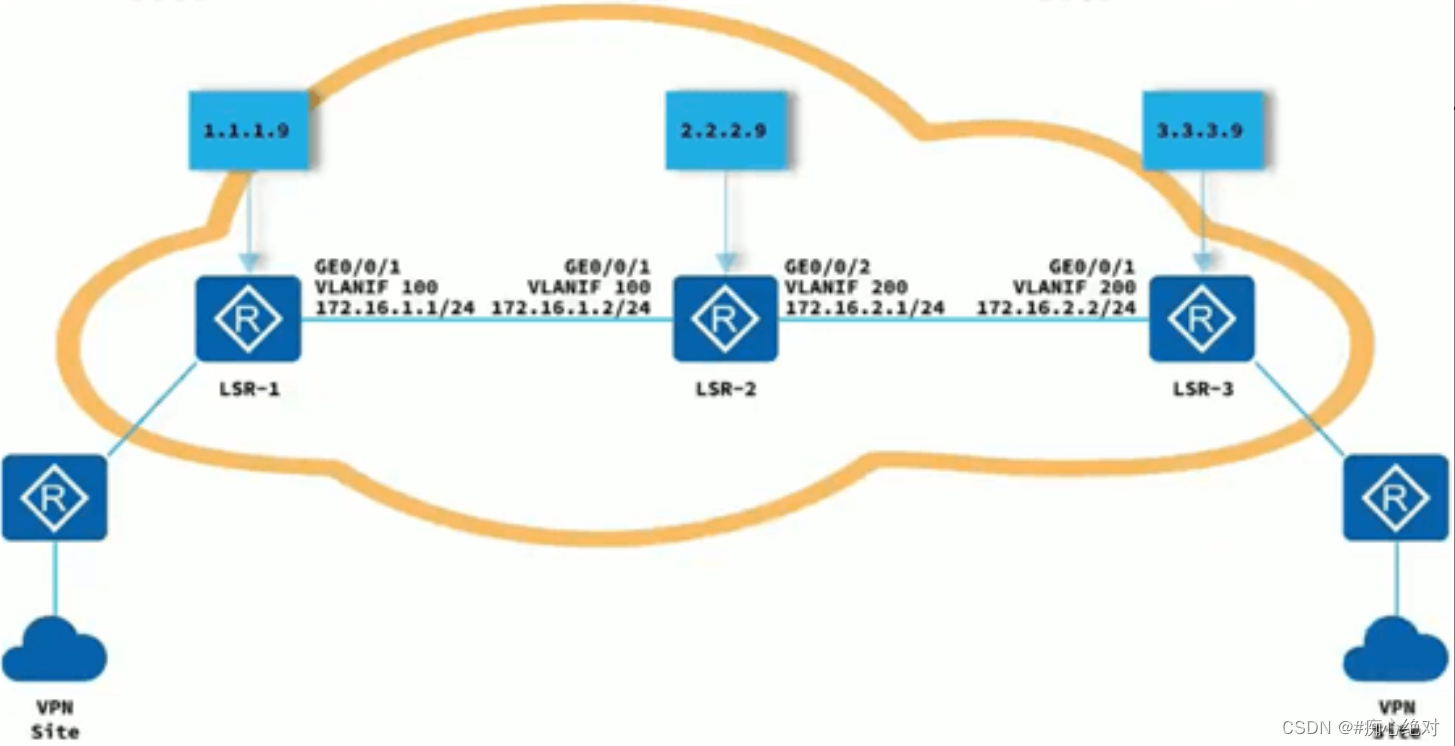
2024上半年网络工程师考试《应用技术》试题一
阅读以下说明,回答问题。 【说明】 MPLS基于(1)进行转发,进行MPLS标签交换和报文转发的网络设备称为(2),构成MPLS域(MPSDomain)。位于MPLS域边缘、连接其他网络的LSR称为(3),区域内部的LSR称为核心LSR(CoreLSR)IP报文进入MPLS网络时…...

pnpm介绍
PNPM 是一个 JavaScript 包管理器,类似于 npm 和 Yarn。它的全称是 "Performant npm",主要设计目标是优化包的安装和管理过程,以提升速度和效率。PNPM 的主要特点包括: 符号链接(Symlink)&#x…...

Linux内核的启动过程(非常详细)零基础入门到精通,收藏这一篇就够了
Linux内核的生成过程 内核的生成步骤可以概括如下: ① 先生成 vmlinux,这是一个elf可执行文件。② 然后 objcopy 成 arch/i386/boot/compressed/vmlinux.bin,去掉了原 elf 文件中一些无用的section等信息。③ gzip 后压缩为 arch/i386/boot…...

相关分析 - 肯德尔系数
肯德尔系数(Kendall’s Tau)是一种非参数统计方法,用于衡量两个变量之间的相关性。它是由统计学家莫里斯肯德尔(Maurice Kendall)在1938年提出的。肯德尔系数特别适用于有序数据,可以用来评估两个有序变量之…...

【咨询】企业数字档案馆(室)建设方案-模版范例
导读:本模版来源某国有大型医药行业集团企业数字档案馆(室)建设方案(一期300W、二期250W),本人作为方案的主要参与者,总结其中要点给大家参考。 目录 1、一级提纲总览 2、项目概述 3、总体规…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
