普通二叉树的操作
普通二叉树的操作
- 1. 前情说明
- 2. 二叉树的遍历
- 2.1 前序、中序以及后序遍历
- 2.1.1 前序遍历
- 2.1.2 中序遍历、后序遍历
- 2.2 题目练习
- 2.2.1 求一棵二叉树的节点个数
- 2.2.2 求一棵二叉树的叶节点个数
- 2.2.3 求一棵二叉树第k层节点的个数
- 2.2.4 求一棵二叉树的深度
- 2.2.5 在一棵二叉树中查找值为x的节点
- 2.2.6 销毁一棵二叉树
- 2.3 二叉树的层序遍历
- 2.4 题目练习
- 2.4.1 判断一棵二叉树是否是完全二叉树
1. 前情说明
本文主要是针对二叉树的链式结构操作进行讲解。
对于普通二叉树的学习,已经不能像之前学线性表,堆等数据结构那样,围绕增删查改来进行操作学习。说到底,对于普通二叉树的增删查改是没有意义的。树形结构本身相对线性结构就更复杂,而且普通二叉树对于数据的操作又不能达到一些规律性的性质,种种原因都限制了普通二叉树的增删改查操作。如果非要进行数据的增删改查,不如去选择操作更方便的结构。比如在数据存储上,与普通二叉树复杂的存储结构相比,不如去选择顺序表,链表等更简单的结构进行数据的存储,这类数据结构对数据的维护也会更容易。
既然如此,那我们学习普通二叉树的意义何在呢?
- 为学习更复杂更有意义的二叉树做储备。
- 很多二叉树的OJ算法题目都是出在普通二叉树上的。
所以,对于普通二叉树的操作,本文会涉及几道题目的练习,方便大家认识理解。
说到这里,既然不学增删查改,那还学什么呢?
那当然需要学习的是对普通二叉树的遍历和结构控制了。
2. 二叉树的遍历
学习二叉树的结构,最简单的方式就是遍历。所谓二叉树的遍历是指按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。而访问节点所做的操作就依赖于具体的应用问题了。
遍历是二叉树最重要的操作之一,也是在二叉树上进行其它操作的基础。
在进行遍历之前,还是再来看一下二叉树的概念吧。
二叉树是:
- 空树
- 非空:由根节点,根节点的左子树,根节点的右子树组成
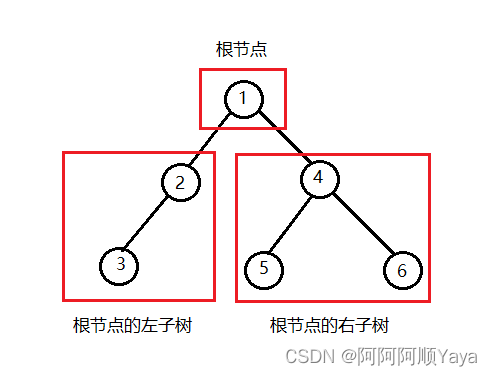
从概念中可以看出,二叉树的定义是递归式的,因此要注意的是,后续各种操作中基本都是按照该递归概念实现的。
同时,据此可以给出二叉树节点的定义如下:
typedef int BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;//存放左子树的根节点地址struct BinaryTreeNode* right;//存放右子树的根节点地址BTDataType data;//根节点的数据域
}BTNode;
2.1 前序、中序以及后序遍历
按照规则,二叉树的遍历有三种递归结构的遍历:
- 前序遍历(也叫先序遍历,先根遍历) —— 访问根节点的操作发生在遍历其左右子树之前。
- 中序遍历(也叫中根遍历) —— 访问根节点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(也叫后根遍历) —— 访问根节点的操作发生在遍历其左右子树之后。
2.1.1 前序遍历
根据先根节点,再左子树,再右子树的顺序走一遍,大致可以得到如下图所示的遍历轨迹。
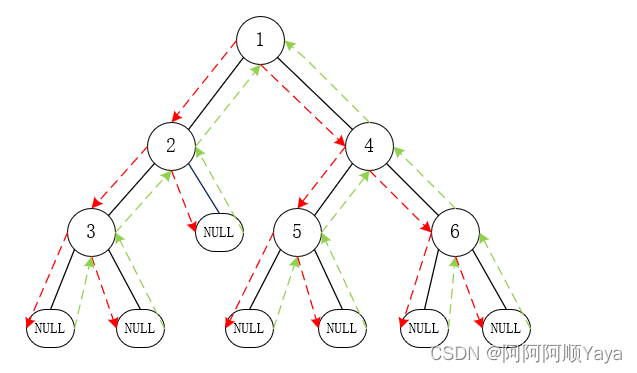
先从根节点1开始遍历,根节点1遍历之后,就开始遍历左子树,
再从左子树的根节点2开始遍历,根节点2遍历之后,又开始遍历根节点2的左子树,
再从左子树的根节点3开始遍历,跟节点3遍历之后,又开始遍历跟节点3的左子树,
但是根节点3的左子树为空,于是路线直接返回到根节点3,开始遍历根节点3的右子树,
但是根节点3的右子树为空,于是路线直接返回到根节点3,此时根节点3所在的子树前序遍历已经完成,所以路线直接返回到根节点2,开始遍历跟节点2的右子树,
但是根节点2的右子树为空,于是路线直接返回到根节点2,此时根节点2所在的子树前序遍历已经完成,所以路线直接返回到根节点1,开始遍历跟节点1的右子树,
再从右子树的根节点4开始遍历,根节点4遍历之后,又开始遍历根节点4的左子树,
再从左子树的根节点5开始遍历,根节点5遍历之后,又开始遍历根节点5的左子树,
但是根节点5的左子树为空,于是路线直接返回到根节点5,开始遍历根节点5的右子树,
但是根节点5的右子树为空,于是路线直接返回到根节点5,此时根节点5所在的子树前序遍历已经完成,所以路线直接返回到根节点4,开始遍历跟节点4的右子树,
再从右子树的根节点6开始遍历,根节点6遍历之后,又开始遍历根节点6的左子树,
但是根节点6的左子树为空,于是路线直接返回到根节点6,开始遍历根节点6的右子树,
但是根节点6的右子树为空,于是路线直接返回到根节点6,此时根节点6所在的子树前序遍历已经完成,所以路线直接返回到根节点4,此时根节点4所在的子树前序遍历已经完成,所以路线直接返回到根节点1,此时根节点1所在的子树前序遍历已经完成,也就是整棵树的前序遍历已经完成了。
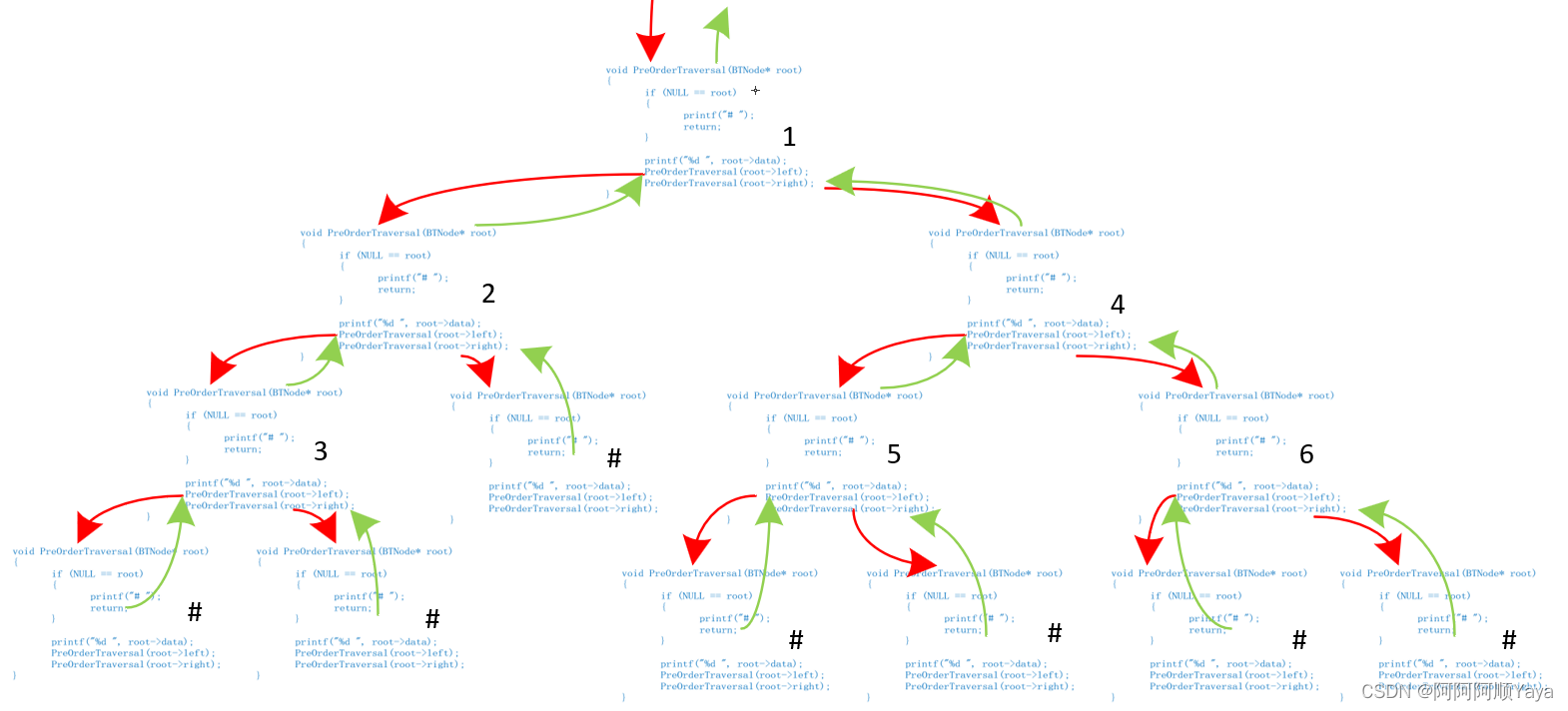
根据上述遍历过程,当遍历时遇到空时,过程会返回;子树的前序遍历完成之后,过程会返回。根据此思路,将其实现可得如下递归代码:
void PreOrderTraversal(BTNode* root)
{if (NULL == root){printf("# ");//打印“#”代表节点为空return;}printf("%d ", root->data);PreOrderTraversal(root->left);PreOrderTraversal(root->right);
}
根据函数调用的次序过程,尝试画出其调用路线如下(红色代表递归调用,绿色代表调用返回,“#”代表子树为空):
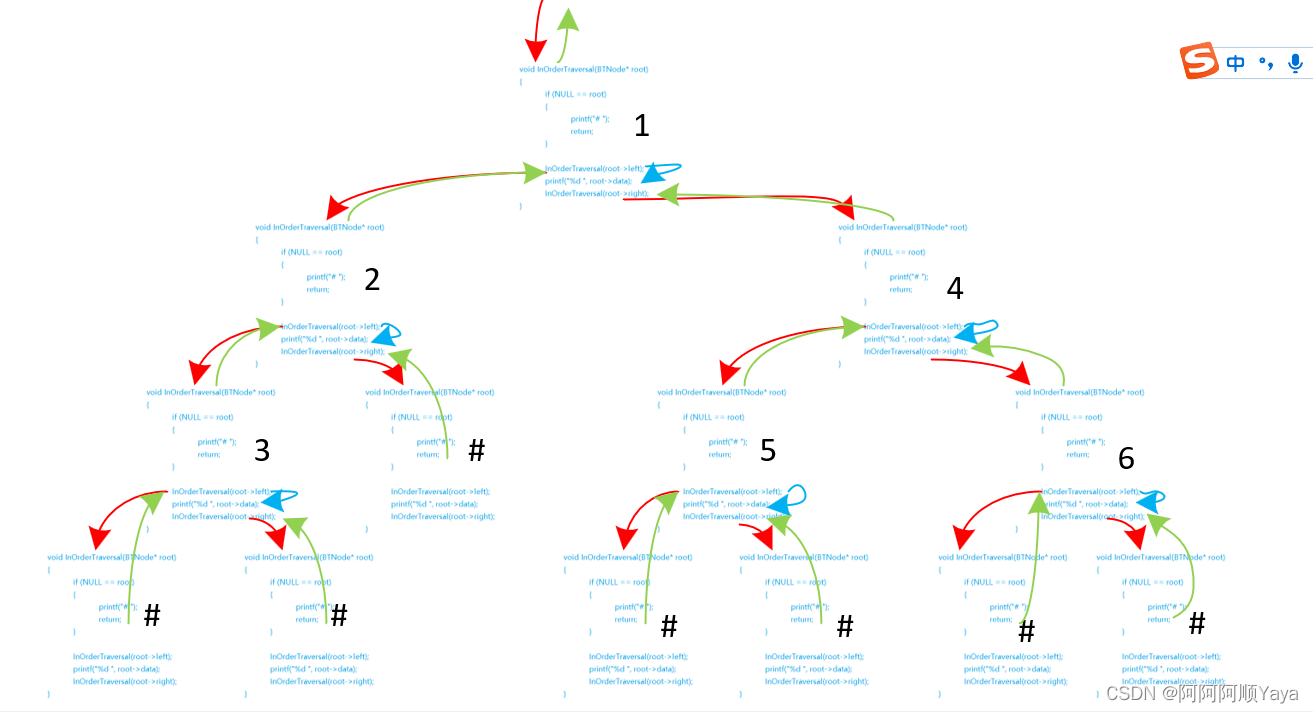
2.1.2 中序遍历、后序遍历
同理,
根据中序遍历:先左子树,再根节点,再右子树
和后序遍历:先左子树,再右子树,在根节点
的遍历过程(😄不再赘述文字😄),
将其实现可分别得到如下递归代码和调用路线图:
//中序遍历
void InOrderTraversal(BTNode* root)
{if (NULL == root){printf("# ");return;}InOrderTraversal(root->left);//先左子树printf("%d ", root->data);//再根节点InOrderTraversal(root->right);//再右子树
}
//后序遍历
void PostOrderTraversal(BTNode* root)
{if (NULL == root){printf("# ");return;}PostOrderTraversal(root->left);//先左子树PostOrderTraversal(root->right);//再右子树printf("%d ", root->data);//再根节点
}
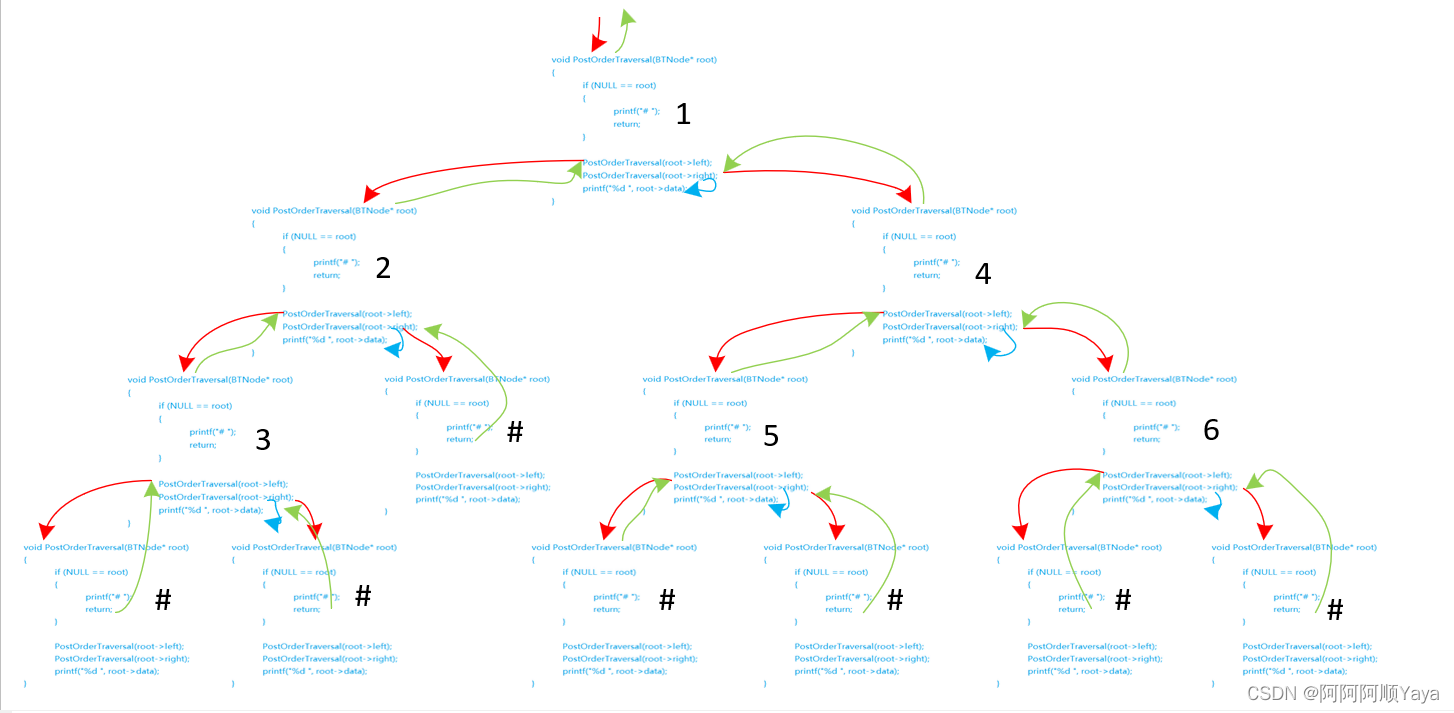
根据以上对于前中后序的递归遍历,我们可以打印出遍历结果分别如下:
前序遍历:1 2 3 # # # 4 5 # # 6 # #
中序遍历:# 3 # 2 # 1 # 5 # 4 # 6 #
后序遍历:# # 3 # 2 # # 5 # # 6 4 1
这里可以告诉大家一种取巧的方法来判断给定一棵树的前中后序遍历结果:
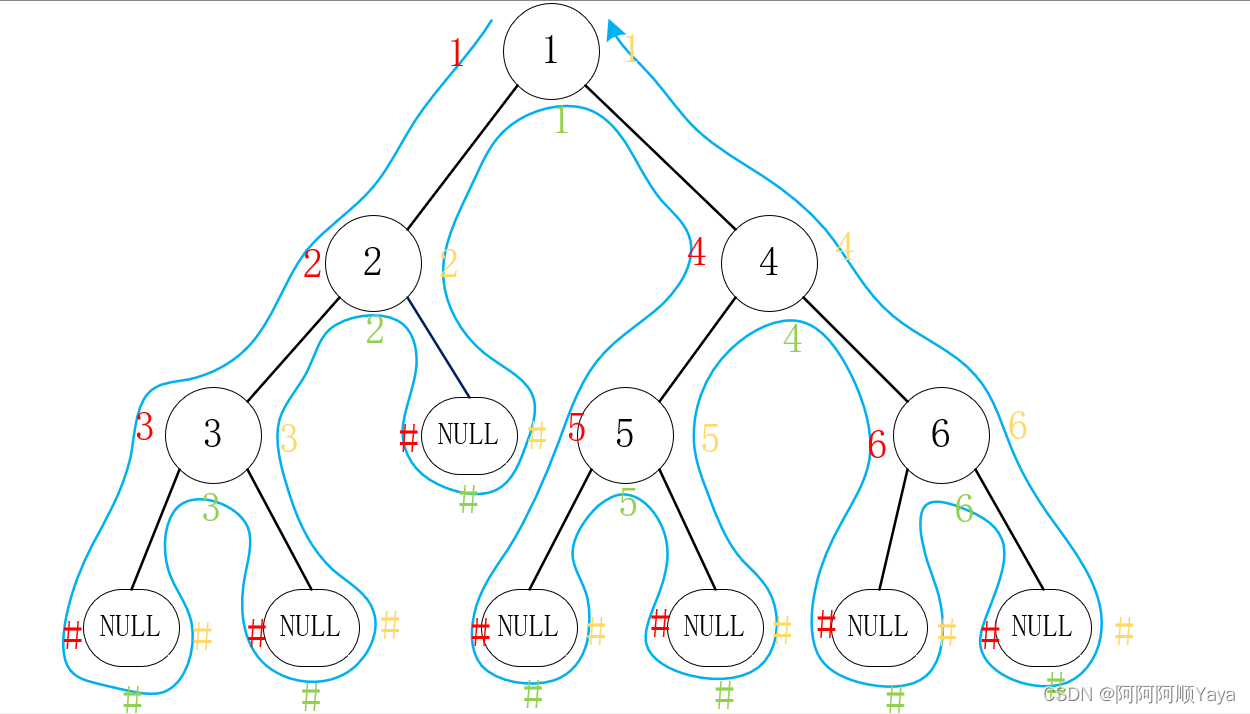
如图所示,
先画图将空节点补全,再从根节点左边开始沿着树的结构画出如图所示的蓝色路线图。
前序遍历的结果就是沿着路线图标记的红色结果,每一个标记都在节点的左边;
中序遍历的结果就是沿着路线图标记的绿色结果,每一个标记都在节点的下边;
前序遍历的结果就是沿着路线图标记的黄色结果,每一个标记都在节点的右边。
2.2 题目练习
了解了这些遍历方式之后,我们可以来看几个题。
2.2.1 求一棵二叉树的节点个数
首先要从二叉树的概念入手。要求一棵二叉树的节点个数,无非就是求二叉树的根节点个数+左子树的节点个数+右子树的节点个数。如果遇到空树,就不是真的节点,返回0即可。但是根节点的话,不能直接返回,要先求出左子树的节点个数+右子树的节点个数,然后再加上根节点的一个数量一齐返回才行。所以可以考虑到用后序遍历完成。
参考代码如下:
int TreeSize(BTNode* root)
{return NULL == root ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
其实也可以使用树的其它遍历方式来完成节点个数的统计。本思想就是额外定义一个计数的变量如count,先初始化为0,在遍历过程中,每遍历到一个节点,如果节点为空,就返回;不为空,count就加1。遍历完成之后,count中存放的数据,就是该树的节点个数了。
这里给出前序遍历作为参考。
void TreeSize(BTNode* root)
{if (NULL == root){return;}++count;TreeSize(root->left);TreeSize(root->right);
}
2.2.2 求一棵二叉树的叶节点个数
首先要知道的是叶节点就是指左右子树都为空的节点。还是从二叉树的概念入手,要求一棵二叉树的叶节点个数,可以分三种情况考虑。
如果根节点为空,就是该树没有节点,也就是没有叶节点,返回0即可。
如果根节点是叶节点,就是该树只有一个叶节点,返回1即可。
如果根节点不是叶节点,那叶节点就只存在于根节点的左右子树中,那就去对根节点的左右子树去进行叶节点的计算,然后返回左右子树中的叶节点的加和即可。
根据上述思路,可以给出参考代码如下:
int TreeLeafSize(BTNode* root)
{if (NULL == root){return 0;}return NULL == root->left && NULL == root->right ? 1 : TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
对于叶节点个数的统计,也可以像树的节点数的统计那样,定义一个计数的变量count来完成,思路和上述类似,就不再赘述。
直接上代码:
void TreeLeafSize2(BTNode* root)
{if (NULL == root){return;}if (NULL == root->left && NULL == root->right){++count;return;}TreeLeafSize(root->left);TreeLeafSize(root->right);}
2.2.3 求一棵二叉树第k层节点的个数
前请说明:这里以根节点的层数为第1层来考虑。
要求第k层的节点个数,要知道这个k是相对于整棵树的根节点(也就是第1层)而言的。言外之意就是,如果是相对第2层而言,那要求的就变成了第k-1层的节点个数。如此递推下去,就可以看做是求第1层的节点个数,那第1层的节点个数自然是只有一个了(这也是函数递归的出口所在)。
根据上述思路,可以给出如下参考代码:
int TreeKLevel(BTNode* root, int k)
{assert(k >= 1);//k要大于等于1才合法if (NULL == root){//如果根节点为空,整棵树中都没有节点,第k层节点数自然为0return 0;}if (1 == k){//递归出口return 1;}return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);}
2.2.4 求一棵二叉树的深度
前请说明:这里以根节点的层数为第1层来考虑。
从二叉树的概念入手。一棵二叉树的深度,无非是根节点的深度加上左右子树深度更大者的深度。
鉴于此,可以给出如下参考代码:
int TreeDepth(BTNode* root)
{if (NULL == root){//如果根节点为空,深度为0return 0;}int leftDepth = TreeDepth(root->left);//左子树的深度计算int rightDepth = TreeDepth(root->right);//右子树的深度计算//取深度较大者 + 根节点的深度(1)if (leftDepth > rightDepth){return leftDepth + 1;}else{return rightDepth + 1;}
}
2.2.5 在一棵二叉树中查找值为x的节点
假设二叉树中每个节点的值都不一样,找到了,返回节点地址;找不到,返回NULL。
这一题还是从二叉树的概念入手,要在一棵二叉树中寻找值为x的节点。那这个节点如果存在的话,无非是存在于三个地方:根节点中,左子树中,右子树中。这三个地方都没找到的话,就返回NULL。
根据上述思路,可以给出如下参考代码:
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (NULL == root){//根节点为空,整棵树为空,自然没有要找的节点。return NULL;}//先找根节点if (x == root->data){return root;}//再找左子树BTNode* retLeft = TreeFind(root->left, x);if (retLeft != NULL){return retLeft;}//再找右子树BTNode* retRight = TreeFind(root->right, x);if (retRight != NULL){return retRight;}//都没找到返回NULLreturn NULL;
}
2.2.6 销毁一棵二叉树
从二叉树的概念入手。销毁一棵二叉树,无非是销毁这棵二叉树的三个部分,即:根节点,根节点的左子树,根节点的右子树。但这里的销毁必须要遵循一定的顺序,是不能先销毁根节点的。因为根节点如果首先被销毁了,那根节点中所存储的左右子树中的根节点的地址,就也被销毁了,就无法找到左右子树所在的空间,不能将其进行释放了。所以根节点的销毁需要在左右子树之后,这正是所谓的后序遍历了。
鉴于此,可以给出如下参考代码:
void TreeDestroy(BTNode* root)
{if (NULL == root){return;}TreeDestroy(root->left);TreeDestroy(root->right);free(root);
}
对于以上题目的函数递归调用流程,大家可以像二叉树的遍历一样,多画图,去分析调用和返回的执行路线,那样可以帮助大家更好地理解和掌握。
2.3 二叉树的层序遍历
二叉树的前中后序遍历,是属于深度优先方向上的遍历。而层序遍历,是属于广度优先方向上的遍历。那下面就一起来看看层序遍历和之前的遍历有什么不同吧。
层序遍历
设二叉树的根节点所在层数为1。层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第3层上的节点,以此类推,自上而下,自左至右逐层访问树的节点的过程就是层序遍历了。
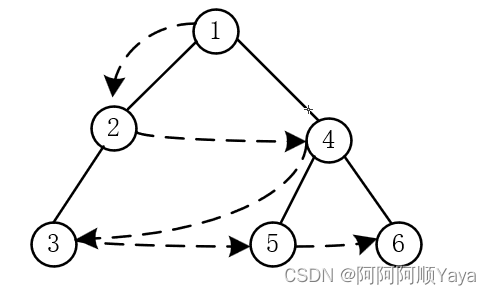
广度优先搜索一般都会借助队列数据结构来完成,这里下面也是使用队列来完成操作的。
但因为这里使用的是C语言,所以还需要自己写一个队列做准备(如果使用的语言本身有符合队列性质的结构可以忽略),需要的小伙伴也可以从阿顺的这篇博文链式队列(C语言实现)获取。
好了,既然有了队列,该如何利用队列的各种性质操作来完成层序遍历呢?
我们可以利用队列先进先出的性质来完成层序遍历的过程。
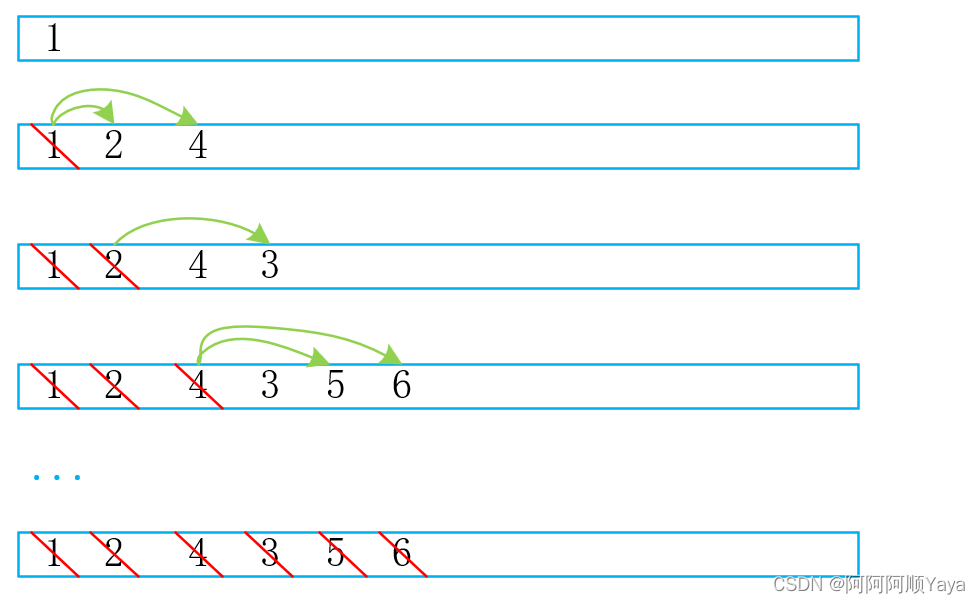
首先,当树的根节点存在时,层序遍历第一个遍历的肯定是根节点。将根节点的数据进行入队,此时,根节点的数据就入队完成了。

接下来该入树的第二层的数据了,也就是2和4。那该如何将他们入队呢?
可以知道的是,他们是根节点的左右子树中的根节点,所以根节点1中的左右指针域存放的有它们的地址,可以通过根节点找到它们。然后将他们进行入队。但是要遵循先左子树后右子树的顺序进行入队。

到第三层的数据入队了,它们分别来自节点2为根的子节点和结点4为根的子节点。同样是通过上一层的节点中的指针域来找到它们进行入队,并且要遵循先左子树后右子树的顺序。
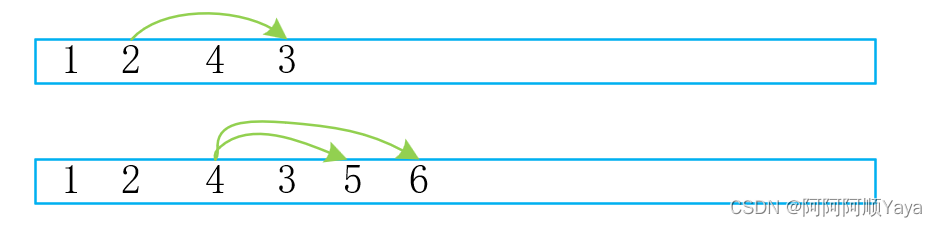
好了,到此树中的所有数据都入队了,再将他们顺序出队,就得到了层序遍历的结果了。
根据此思想,可以给出如下参考代码:
void LevelOrderTraversal(BTNode* root)
{Queue q;QueueInit(&q);//初始化队列//根节点存在,就直接入队列//入的是结点的地址,因为这样才能在后续通过指针域将其它节点入队if (NULL != root){QueuePush(&q, root);}while (!QueueEmpty(&q)){//如果队列不为空,执行以下操作//取队头元素BTNode* front = QueueFront(&q);//这里将队头元素交给front后,直接出队头数据了,和上面的图画的有出入//真实的过程在下图中QueuePop(&q);printf("%d ", front->data);if (NULL != front->left){QueuePush(&q, front->left);}if (NULL != front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
在理解了上述层序遍历的过程,下面趁热打铁就来看一道题。
2.4 题目练习
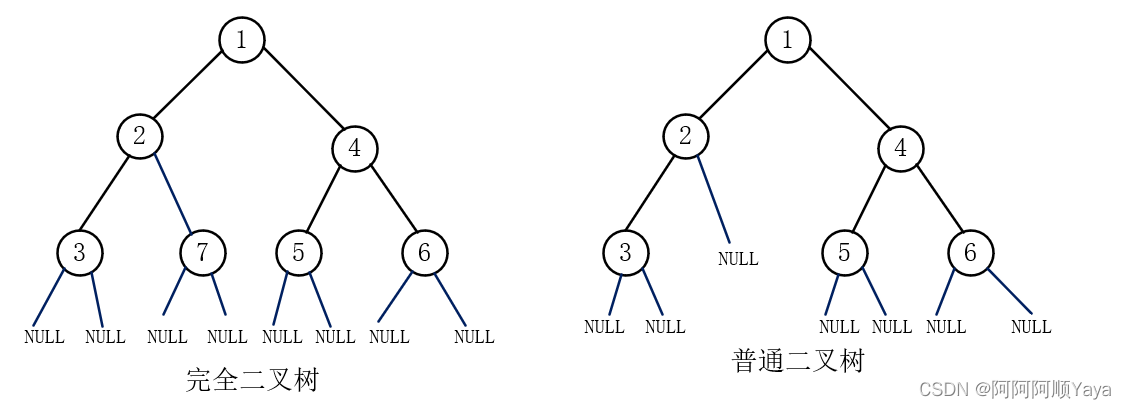
2.4.1 判断一棵二叉树是否是完全二叉树
是返回true,不是返回false。
完全二叉树的概念这里就不在赘述,需要的小伙伴可以参考阿顺的这篇博文树与二叉树(概念篇)进行学习。
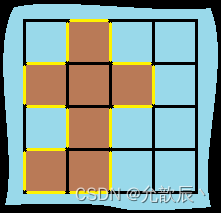
大家可以尝试画一画,在将一棵二叉树的空节点也考虑入队的情况下,一棵完全二叉树在入队后,队列中的数据形态是什么样子的;一棵非完全二叉树在入队后,队列中的数据形态又是什么样子的。画过之后,相信大家很快就会明白其中的意思了。
下面以该图为例,带大家一起看看。
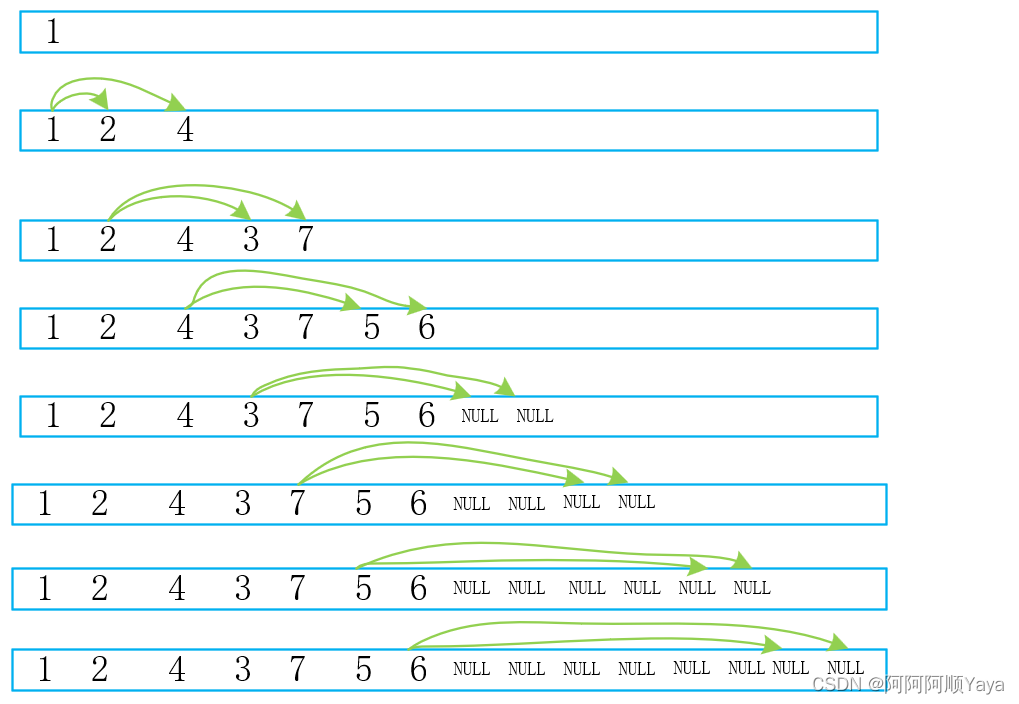
完全二叉树入队:
普通二叉树入队:
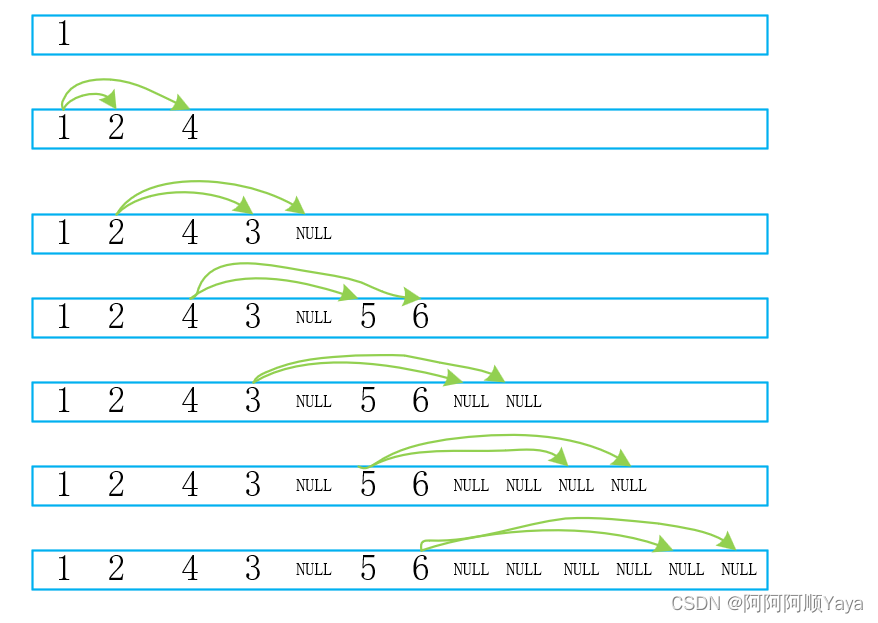
可以发现完全二叉树入队后,树的非空节点和空节点是“泾渭分明”的,而普通二叉树的非空节点和空节点是“鱼龙混杂”的。
这就为我们判断一棵二叉树是完全二叉树还是普通二叉树提供了思路。
bool TreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (NULL != root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueuePush(&q, front->left);QueuePush(&q, front->right);}else//fornt==NULL,循环结束{break;}}while (!QueueEmpty(&q)){//如果NULL后面还有非空节点,就返回falseif (QueueFront(&q) != NULL){//队列销毁,防止内存泄漏QueueDestroy(&q);return false;}QueuePop(&q);}//NULL后面不存在非空节点,返回trueQueueDestroy(&q);return true;
}
好了,本文对于普通二叉树的讲解算是完结了。虽然费劲心机想写得大家能一遍看懂,但感觉还是很难,真的是写得有些精疲力尽了,但最后还是希望能对大家的学习有一点点帮助吧。
相关文章:

普通二叉树的操作
普通二叉树的操作1. 前情说明2. 二叉树的遍历2.1 前序、中序以及后序遍历2.1.1 前序遍历2.1.2 中序遍历、后序遍历2.2 题目练习2.2.1 求一棵二叉树的节点个数2.2.2 求一棵二叉树的叶节点个数2.2.3 求一棵二叉树第k层节点的个数2.2.4 求一棵二叉树的深度2.2.5 在一棵二叉树中查找…...

Oracle:递归树形结构查询功能
概要树状结构通常由根节点、父节点(PID)、子节点(ID)和叶节点组成。查询语法SELECT [LEVEL],* FROM table_name START WITH 条件1 CONNECT BY PRIOR 条件2 WHERE 条件3 ORDER BY 排序字段说明:LEVEL—伪列࿰…...

MongoDB数据库性能监控详解
目录一、MongoDB启动超慢1、启动日常卡住,根本不用为了截屏而快速操作,MongoDB启动真的超级慢~~2、启动MongoDB配置服务器,间歇性失败。3、查看MongoDB日志,分析“MongoDB启动慢”的原因。4、耗时“一小时”,MongoDB启…...

python不要再使用while死循环,使用定时器代替效果更佳!
在python开发的过程中,经常见到小伙伴直接使用while True的死循环sleep的方式来保存程序的一直运行。 这种方式虽然能达到效果,但是说不定什么时候就直接崩溃了。并且,在Linux环境中在检测到while True的未知进程就会直接干掉。 面对这样的…...
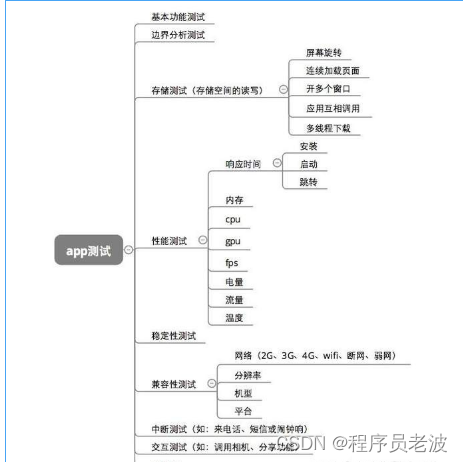
什么是接口测试?十年阿里测试人教你怎样做接口测试
一 什么是接口? 接口测试主要用于外部系统与系统之间以及内部各个子系统之间的交互点,定义特定的交互点,然后通过这些交互点来,通过一些特殊的规则也就是协议,来进行数据之间的交互。接口测试主要用于外部系统与系统之…...
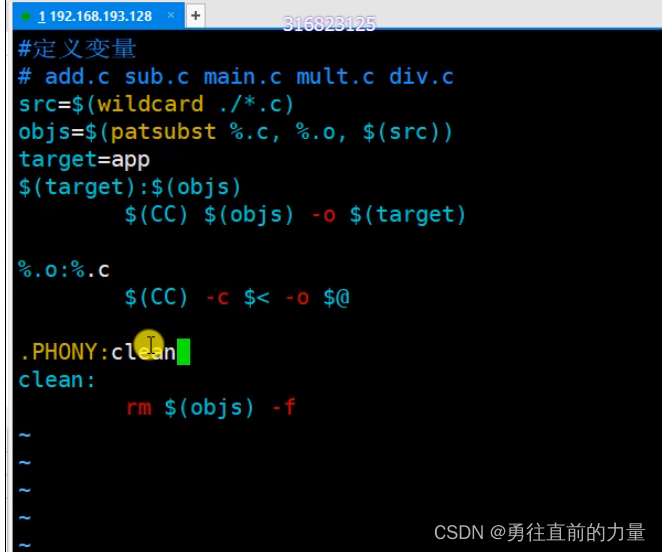
1.10-1.12 Makefile
1. Makefile简介 举个栗子,如下为redis-5.0.10的项目目录,有很多的文件 有了Makefile文件,可以简单的make一下就可以对项目文件进行编译,最终生成可执行程序。 2. Makefile栗子1 首先,创建vim Makefile按照PPT里的格…...
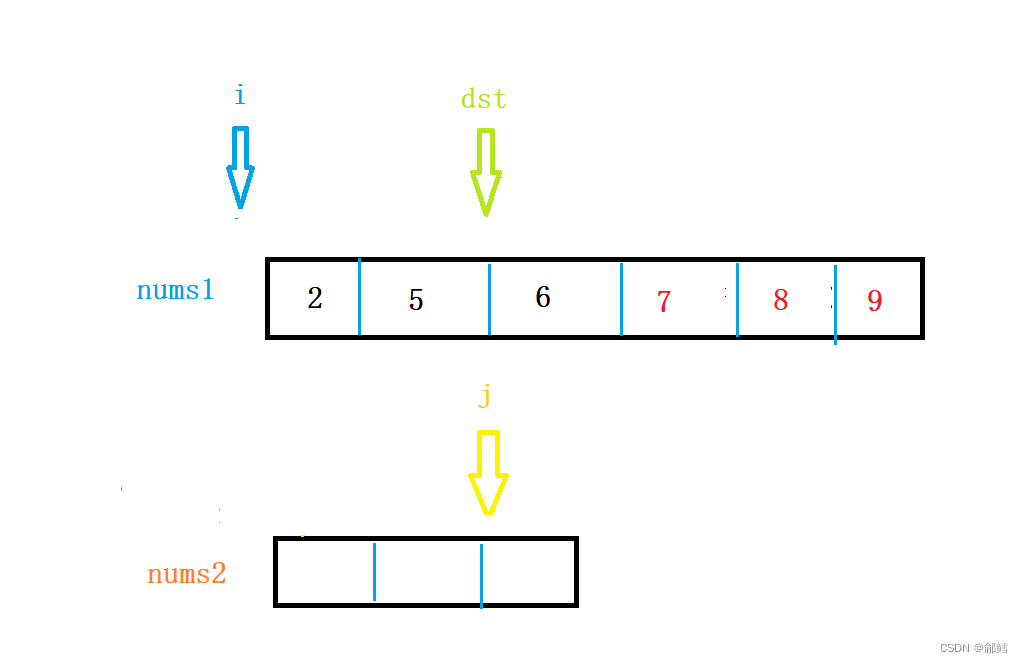
Leetcode. 88合并两个有序数组
合并两个有序数组 文章目录归并思路二归并 核心思路: 依次比较,取较小值放入新数组中 i 遍历nums1 , j 遍历nums2 ,取较小值放入nums3中 那如果nums[i] 和nums[j]中相等,随便放一个到nums3 那如果nums[i] 和nums[j]中相…...
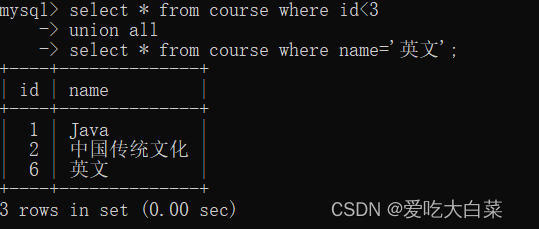
【数据库】数据库查询(进阶命令详解)
目录 1.聚合查询 1.1聚合函数 COUNT函数 SUM函数 AVG函数 MAX函数 MIN函数 1.2GROUP BY子句 1.3HAVING 2.联合查询 2.1内连接 2.2外连接 2.3自连接 2.4子查询 3.合并查询 写在前面: 文章截图均是每个代码显示的图。数据库对代码大小写不敏感&am…...

参数缺省和函数重载讲解
一路风雨兼程磨砺意志,三载苦乐同享铸就辉煌 目录 1.参数缺省的概念 2.参数缺省的用法 3.缺省参数分类 3.1.全缺省参数 3.2.半缺省参数 4.函数重载的概念 5.函数重载的用法 6.函数重载的原理 1.参数缺省的概念 一般情况下,函数调用时的实参个数应…...

关于召开2023第八届国际发酵培养基应用发展技术论坛的通知
生物发酵培养基是影响产业技术水平、环境友好程度的重要影响因素,为进一步实现生物发酵培养基的稳定可控、高效生产以及绿色安全,进一步推动生物技术的创新升级、绿色低碳循环生产,需要加强跨界联合,集中优势力量,突破…...
Java之深度优先(DFS)和广度优先(BFS)及相关题目
目录 一.深度优先遍历和广度优先遍历 1.深度优先遍历 2.广度优先遍历 二.图像渲染 1.题目描述 2.问题分析 3代码实现 1.广度优先遍历 2.深度优先遍历 三.岛屿的最大面积 1.题目描述 2.问题分析 3代码实现 1.广度优先遍历 2.深度优先遍历 四.岛屿的周长 1.题目描…...

【链表OJ题(四)】反转链表
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录链表OJ题(四)1. 反转…...
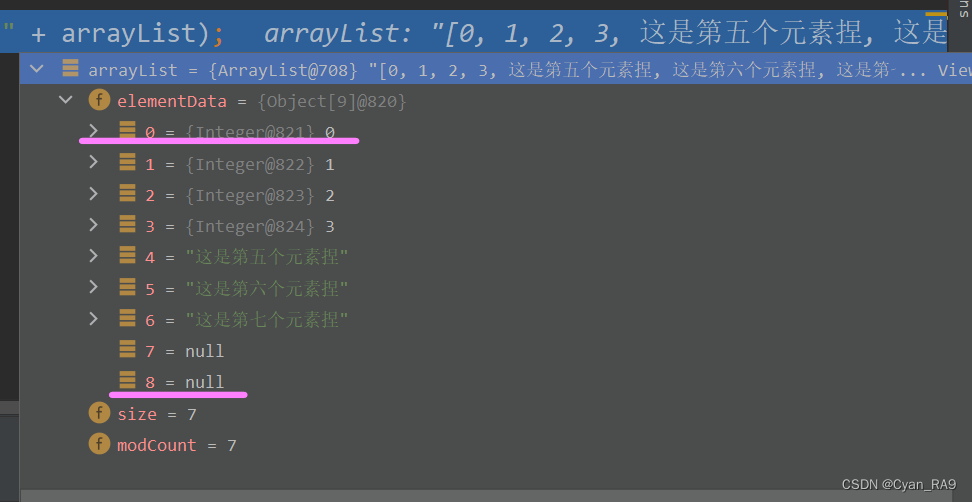
java ArrayList源码分析(深度讲解)
ArrayList类的底层实现ArrayList类的断点调试空参构造的分步骤演示(重要)带参构造的分步骤演示一、前言大家好,本篇博文是对单列集合List的实现类ArrayList的内容补充。之前在List集合的万字详解篇,我们只是拿ArrayList演示了List…...

【网络编程】零基础到精通——NIO基础三大组件和ByteBuffer
一. NIO 基础 non-blocking io 非阻塞 IO 1. 三大组件 1.1 Channel & Buffer channel 有一点类似于 stream,它就是读写数据的双向通道,可以从 channel 将数据读入 buffer,也可以将 buffer 的数据写入 channel,而之前的 st…...

操作系统 - 1. 绪论
目录操作系统基本概念概念特征功能操作系统的分类与发展手工操作单道批处理系统多道批处理系统分时系统实时系统操作系统的运行环境CPU 运行模式中断和异常的处理系统调用程序的链接与装入程序运行时内存映像和地址空间操作系统的体系结构操作系统的引导操作系统基本概念 概念…...

详谈parameterType与resultType的用法
resultMap 表示查询结果集与java对象之间的一种关系,处理查询结果集,映射到java对象。 resultMap 是一种“查询结果集---Bean对象”属性名称映射关系,使用resultMap关系可将将查询结果集中的列一一映射到bean对象的各个属性&#…...

【Linux】进程概念、fork() 函数 (干货满满)
文章目录📕 前言📕 进程概念📕 Linux下查看进程的两种方法方法一方法二📕 pid() 、ppid() 函数📕 fork() 函数、父子进程初识再理解📕 fork做了什么📕 如何理解 fork 有两个返回值📕…...
【动态规划】最长上升子序列、最大子数组和题解及代码实现
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

Ajax进阶篇02---跨域与JSONP
前言❤️ 不管前方的路多么崎岖不平,只要走的方向正确,都比站在原地更接近幸福 ❤️Ajax进阶篇02---跨域与JSONP一、Ajax进阶篇02---跨域与JSONP(1)同源策略1.1 什么是同源1.2 什么是同源策略(2)跨域2.1 什…...
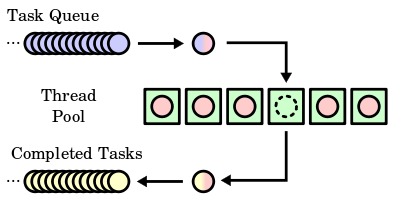
C 语言编程 — 线程池设计与实现
目录 文章目录目录线程池(Thread Pool)tiny-threadpool数据结构设计Task / JobTask / Job QueueWorker / ThreadThread Pool ManagerPublic APIsPrivate Functions运行示例线程池(Thread Pool) 线程池(Thread Pool&am…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
