数据结构入门6-1(图)
目录
注
图的定义
图的基本术语
图的类型定义
图的存储结构
邻接矩阵
1. 邻接矩阵表示法
2. 使用邻接矩阵表示法创建无向网
3. 邻接矩阵表示法的优缺点
邻接表
1. 邻接表表示法
2. 通过邻接表表示法创建无向图
3. 邻接表表示法的优缺点
十字链表(有向图)
邻接多重表(无向图)
图的遍历
深度优先搜索(DFS)
广度优先搜索
注
本笔记参考《数据结构(C语言版)(第2版)》
图是一种比线性表和树更复杂是数据结构。在线性表中,数据元素之间存在线性关系;在树形结构中,数据元素之间存在层次关系。但是,到了图结构中,结点之间的关系可以是任意的,这意味着任意两个数据元素都可能相关。
图的定义
||| 图(Graph,记为G)由两个集合V和E组成,记为G(V, E)。其中:
- V(顶点):顶点的有穷非空集合(V(G)表示图G的顶点集合);
- E(边):V中顶点偶对的有穷集合,偶对称的顶点连成了边(E(G)表示图G的边集合,可以为空。为空时,图G只有顶点) 。
| 有向图 | 无向图 | |
| 使用的括号 | < > | ( ) |
| 方向 | <x, y> 表示从顶点x到顶点y的一条有向边 | 无特定方向 |
| 边的区别 | <x, y> 和 <y, x> 是不同的两条边 | (x, y) 和 (y, x) 是同一条边 |
对于有向图而言,<x, y> 也可以被称为一条弧。其中,x为弧尾,y为弧头。
【例子】

图的基本术语
用n表示图中的顶点,用e表示边的数目,图有如下的基本术语:
| 名称 | 解释 |
| 子图 | 设图G = (V, E),图G' = (V', E'): 若V' ⊆ V,且E' ⊆ E,则G'是G的子图。 |
| 无向完全图和有向完全图 | • 无向完全图:①是无向图;②具有n(n-1)/2条边。 • 有向完全图:①是有向图;②具有n(n-1)条弧。 |
| 稀疏图和稠密图 | • 稀疏图:边/弧很少的图(譬如e<nlog₂n)。 • 稠密图:边/弧很多的图。 |
| 权和网 | • 权:每条边上具有的,有某种含义的数值。 • 网:带权的图被称为网。 |
| 邻接点 | 两个结点由一条无向边或者有向边关联,则称这两个结点为邻接点。 |
| 度、入度和出度 | • 顶点v的度:和v关联的边的数目,记为TD(v)。 • 对于有向图,顶点的度分为入度和出度: 入度:以顶点为头的弧的数目,记为ID(v); 出度:以顶点为尾的弧的数目,记为OD(v)。 有公式:TD(v) = ID(v) + OD(v) |
| 路径和路径长度 | • 路径:是由 顶点v 到 顶点v' 的一个顶点序列(若G是有向图,则路径也是有向的)。 • 路径长度:是一条路径上的边/弧的数目。 |
| 回路(或称 环 ) | 是第一个顶点和最后一个顶点相同的路径。 |
| 简单路径、 简单回路(或称 简单环 ) | • 简单路径:序列中顶点不重复出现的路径。 • 简单回路/简单环:除第一个顶点和最后一个顶点外,其余顶点不重复的回路。 |
| 连通、连通图和连通分量 | • 连通:从 顶点v 到顶点v' 有路径,则称v和v'是连通的。 • 连通图:若图G中任意两个顶点连通,则图G是连通图(例:上图的G₂)。 • 连通分量:即无向图中的极大连通子图。 |
| 强连通图和强连通分量 | • 强连通图:在有向图G中,若对于每一对 v 和 v' ∈ V(v ≠ v'),从 v 到v' 和从 v' 到 v 都有路径,则图G是强连通图。 • 强连通分量:有向图中的极大连通子图被称为有向图的强连通分量。 |
||| 连通图的生成树:
- 是一个极小连通子图(含有图中的所有顶点,是边最少的连通子图);
- 只有足以构成一棵树的n - 1条边。
【例子】

若在上图的生成树中添上一条边,则必定构成一个环。
一棵有n个顶点的生成树仅有n - 1条边。因此:
- 若一个图有n个顶点和少于n - 1条的边,则该图就是非连通图。
- 若一个图有n个顶点和多于n - 1条的边,则该图必定有环。
(注:但是有n - 1条边的图不一定是生成树。)
||| 有向树和生成森林
- 有向树:有一个顶点的入度为0,其余顶点的入度均为1的有向图被称为有向树。
- 生成森林:一个有向图的生成森林由若干棵有向树组成(含有图中所有顶点,但是只有可以构成若干不相交的有向树的弧)。
【例子】

图的类型定义
图的抽象数据类型的定义如下:

图的存储结构
由于图的结构的复杂性,无法通过数据元素在存储区中的物理位置来表示元素之间的关系,所以图是没有顺序存储结构的。可以使用二维数组来表示元素之间的关系,即邻接矩阵表示法。
邻接矩阵
1. 邻接矩阵表示法
邻接矩阵是表示顶点之间相邻关系的矩阵。设G(V, E)是具有n个顶点的图,则G的邻接矩阵是具有如下性质的n阶方阵:

【例子】

------
若G是网(带权的图),则可定义邻接矩阵为:

【例子】

图的邻接矩阵存储表示如下:
#define MVNum 50 //最大顶点数
#define MaxInt 32767 //定义权值的最大值(足够大而不会溢出的数)
typedef char VerTexType; //设置顶点的类型
typedef int ArcType; //设置边的权值类型
typedef struct
{VerTexType vexs[MVNum]; //顶点表ArcType arcs[MVNum][MVNum]; //邻接矩阵int vexnum, arcnum; //图当前的顶点数和边数
}AMGraph;在C语言或者C++中,在头文件中规定了各种类型能够取得的最大值,可以自行调用。
2. 使用邻接矩阵表示法创建无向网
【参考代码:CreateUDN函数】
Status CreateUDN(AMGraph& G)
{//------准备阶段------cin >> G.vexnum >> G.arcnum; //依次输入总顶点数、总边数for (int i = 0; i < G.vexnum; i++) //依次输入点的信息cin >> G.vexs[i];for (int i = 0; i < G.vexnum; i++) //初始化邻接矩阵,将边的权值均设为最大值for (int j = 0; j < G.arcnum; j++)G.arcs[i][j] = MaxInt; //------构建邻接矩阵阶段------for (int k = 0; k < G.arcnum; k++){VerTexType v1, v2;ArcType w;cin >> v1 >> v2 >> w; //v1、v2是一条边所依附的顶点,w是该条边的权值int i = LocateAMGVex(G, v1); //确定v1和v2在G中的位置(即顶点数组的下标)int j = LocateAMGVex(G, v2);G.arcs[i][j] = w; //将边<v1, v2>的权值置为wG.arcs[j][i] = G.arcs[i][j]; //设置对称边}return true;
}【参考代码:LocateAMGVex函数】
对LocateVex函数的要求:遍历顶点数组的下标,并且返回所求顶点的位置。
int LocateAMGVex(AMGraph G, VerTexType v)
{for (int i = 0; i < G.vexnum; i++){if (G.vexs[i] == v)return i;}return -1;
}【算法分析】
上述算法的时间复杂度:O(n²) 。(参考上述算法,也可以通过稍加改动得到无向图、有向网、有向图的创建算法。)
3. 邻接矩阵表示法的优缺点
(1)优点
① 通过对A[i][j]的数值进行观察,可以很快判断出两顶点之间是否有边。
② 通过邻接矩阵,可以轻易计算得到各个顶点的度(出度、入度)。
(2)缺点
① 不便于增删顶点;
②不便于统计边的数目(需要遍历邻接链表,时间复杂度为O(n²));
③ 空间复杂度高,是O(n²),对于稀疏图而言尤其浪费空间。
由于上述邻接法的缺点,就需要有更适合稀疏图的数据结构。由此就引入了邻接表。
邻接表
1. 邻接表表示法
邻接表是图的一种链式存储结构。一般地,邻接表有两部分组成:
- 表头结点表:由表头结点组成,通过顺序结构进行存储,方便访问(表头结点用以存储顶点的相关信息)。

- 边链表:由表示图中关系的2n个边链表组成(边链表由边结点组成)。

由上述数据结构可知:① 在无向图的邻接表中,某顶点的度就是其对应链表中的结点数;② 在有向图中,某一链表中的结点数就是对应结点的出度。但是,若要求得某一结点的入度,就需要遍历整个邻接表。此时为了方便,就需要一个有向图的逆邻链表,如图:

图的邻接表的存储结构(头结点、边结点)可参考下面:
#define MVNum 50 //最大顶点数
#define OtherInfo int //相关信息的类型typedef struct ArcNode //边结点的存储结构
{int adjvex; //该条边指向的结点的位置struct ArcNode* nextarc; //指向与下一条边(对应的结点)OtherInfo info; //和边有关的信息(例如:权值)
}ArcNode;
typedef struct VNode //顶点信息
{VerTexType data;ArcNode* firstarc; //指向与该顶点邻接的第一条边(第一个顶点)
}VNode, AdjList[MVNum];
typedef struct //邻接表
{AdjList vertices; //表本体int vexnum, arcnum; //图的当前顶点数和边数
}ALGraph;2. 通过邻接表表示法创建无向图
【参考代码:CreateUDG函数】
Status CreateUDG(ALGraph& G)
{cin >> G.vexnum >> G.arcnum; //依此输入总顶点数、总边数for (int i = 0; i < G.vexnum; i++) //输入各个顶点,构造表头结点表{cin >> G.vertices[i].data; //输入顶点的值G.vertices[i].firstarc = NULL; //表头结点的指针域置空}for (int k = 0; k < G.arcnum; k++) //输入各边,构造边链表{VerTexType v1, v2; //输入一条边依附的两个顶点cin >> v1 >> v2;int i = LocateALGVex(G, v1); //确定顶点在G.vertices中的位置(序号)int j = LocateALGVex(G, v2);ArcNode* p1 = new ArcNode; //生成新的边结点p1->adjvex = j; //邻接点的序号就是jp1->nextarc = G.vertices[i].firstarc;G.vertices[i].firstarc = p1; //将p1插入顶点i边表的表头ArcNode* p2 = new ArcNode;p2->adjvex = i;p2->nextarc = G.vertices[j].firstarc;G.vertices[j].firstarc = p2; //将p2插入顶点j边表的表头}return true;
}【参考代码:LocateALGVex函数】
类似于LocateAMGVex函数,只是在搜索时稍加改动。
int LocateALGVex(ALGraph G, VerTexType v)
{for (int i = 0; i < G.vexnum; i++){if (G.vertices[i].data == v)return i;}return -1;
}【算法分析】
上述算法的时间复杂度:O(n + e)。(如若需要建立有向图的邻接表,则更加简单。而若要创建有向网的邻接表,则可在info域内输入边的权值。)
注:一个图的邻接矩阵是唯一的,但是邻接表却是不唯一的。
3. 邻接表表示法的优缺点
(1)优点
① 便于增删结点。
② 便于统计边的数目(通过扫描边表即可得到,时间复杂度是O(n + e))。
③ 空间复杂度为O(n + e),空间效率高,适合稀疏图(邻接矩阵表示法更适合稠密图)。
(2)缺点
① 不便于判断顶点之间是否存在边(需要扫描对应边表,最坏情况下时间复杂度为O(n))。
② 不便于计算有向图中各个顶点的度(特别是有向图,为了求得入度,需要遍历各顶点的边表。若采用逆邻接表,则难求出度)。
为了方便求出顶点的入度和出度,接下来就要引入十字链表的概念。
十字链表(有向图)
十字链表是有向图的一种链式存储结构,相当于结合了有向图的邻接表和逆邻接表。十字链表将结点分为了两种 —— 弧结点和边结点:

在十字链表中,弧头相同的弧在同一链表上,弧尾相同的弧也在同一链表上。
【例如】

有向图的十字链表存储表示形式可参考下面:
#define MAX_VERTEX_NUM 20
#define InfoType int
typedef struct ArcBox
{int tailvex, headvex; //该弧的尾和头顶点的位置struct ArcBox* hlink, * tlink; //分别为弧头相同和弧尾相同的弧的链域InfoType* info; //关于该弧的相关信息的指针
}ArcBox;
typedef struct VexNode
{VerTexType data;ArcBox* firstin, * firstout; //分别指向该顶点的第一条入弧和出弧
}VexNode;
typedef struct
{VexNode xlist[MAX_VERTEX_NUM]; //表头向量int vexnum, arcnum; //有向图的当前顶点数和弧数
}OLGraph;如果要进行有向图的十字链表的创建,可以模仿邻接表的创建算法:

建立十字链表的时间复杂度也是O(n + e)。但是十字链表在寻找弧和度上具有更大的优势。
邻接多重表(无向图)
邻接多重表是无向图的一种(很有效的)链式存储结构。由于在邻接表中,一条弧依附的两个顶点分别被存储在不同的链表中,在寻找一条弧对应的两个顶点时存在困难,给某些图的操作带来了不便。所以,就要通过邻接多重表解决这一问题。
类似于十字链表,邻接多重表也由两种不同的结点构成:

【例如】

邻接多重表的类型说明如下:
//------无向图的邻接多重表存储表示------
#define MAX_VERTEX_NUM 20
typedef enum { unvisited, visited } VisitIf;
typedef struct EBox
{VisitIf mark; //是否访问的标记int ivex, jvex; //该条边依附的两个顶点的位置struct EBox* ilink, * jlink; //分别指向依附这两个顶点的下一条边InfoType* info;
}Ebox;
typedef struct VexBox
{VerTexType data;Ebox* firstedge; //指向依附于该顶点的第一条边
}VexBox;
typedef struct
{VexBox adjmulist[MAX_VERTEX_NUM];int vexnum, edgenum; //无向图的当前顶点数和边数
}AMLGraph;邻接多重表的各种基本操作的实现和邻接表类似,实现时可以参考邻接表。

图的遍历
类似于树的遍历,图的遍历也需要从某一结点出发,按照某种方式对图中所有结点进行(仅一次的)访问。但是,图的遍历可能会涉及回路等的问题,这意味着在沿某条路径进行访问时,有可能回到最开始进行访问的结点。为此,就需要对已访问的结点进行标记:
- 一般地,设辅助数组visited[n];
- 辅助数组的初始值均为 0(“false”);
- 将已经过的某一结点对应的visited[i]设为 1(“true”)。
根据搜索路径方向的不同,通常会有两种不同的遍历图的路径:深度优先搜索和广度优先搜索。
深度优先搜索(DFS)
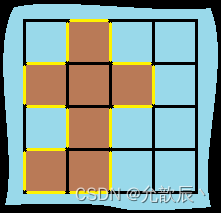
深度优先搜索可以看作是树的先序遍历的一种推广。其的过程用例子表示如下:


![]()
由上图可得到一棵深度优先生成树,如图:

【参考代码:DFS函数,深度优先搜索访问连通图的(递归)算法实现】
//------深度优先搜索遍历连通图(以无向图为例,使用邻接表存储)------
void DFS(ALGraph G, int v) //从第v个顶点开始访问
{cout << G.vertices[v].data; //访问(此处为输出)第v个顶点visited[v] = true; //在标志数组相应位置进行标记for (int w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w)){if (!visited[w]) //对尚未访问的邻接顶点w进行访问DFS(G, w);}
}除DFS函数之外,还牵扯到两个函数:FirstAdjVex() 和 NextAdjVex() ,它们的作用分别是:
▪ FirstAdjVex函数:检查v的所有邻接点w,返回v的第一个邻接点;
▪ NextAdjVex函数:返回v相对于w的下一个邻接点。
由于篇幅有限,下面将仅展示通过邻接表实现的这两个函数。
【参考代码:FirstAdjVex函数】
int FirstAdjVex(ALGraph G, int v)
{if (G.vertices[v].firstarc) //遍历边表return G.vertices[v].firstarc->adjvex;elsereturn -1; //邻接点不存在
}【参考代码:NextAdjVex函数】
int NextAdjVex(ALGraph G, int v, int w)
{ArcNode* p = G.vertices[v].firstarc;while (p && p->adjvex != w) //寻找w指示顶点p = p->nextarc;if (p && p->nextarc)return p->nextarc->adjvex;elsereturn -1;
}注意:上述的情况没有涉及到非连通图的处理。也就是说,当上述遍历执行完毕后,非连通图中一定会有未被访问的顶点。此时需要在图中再次寻找新的起始点(即仍未被访问的结点),再次执行上述步骤,直到图中所有顶点均被访问完毕。
【参考代码:深度优先搜索遍历非连通图(邻接表版本)】
//------对非连通图G进行深度优先搜索------
void DFSTraverse(ALGraph G)
{for (int v = 0; v < G.vexnum; v++) //初始化标志数组visited[v] = false;for (int v = 0; v < G.vexnum; v++) if (!visited[v]) //对尚未访问过的顶点进行函数调用DFS(G, v);
}对于DFSTraverse函数,每调用一次DFS_AL函数,就代表着有一个连通分量。
【算法分析:DFSTraverse函数(以邻接表为例)】
在遍历时,一个顶点只访问一次,之后就不会从该顶点出发进行搜索。故遍历图的实质就是对每个顶点查找其邻接点的过程。设图中顶点数为 n ,边数为 e ,则在邻接表中:
- 查找邻接点的时间复杂度为:O(e);
- 深度优先搜索遍历图的时间复杂度为:O(n + e)。
在邻接矩阵中,查找邻接点的时间复杂度为O(n²)。
广度优先搜索
广度优先搜索类似于数的按层次遍历,依旧以无向图G₄为例:


![]()
同样的,通过上述方法可以得到一棵广度优先生成树,如图:

【参考代码:BFS函数,广度优先搜索遍历连通图(依旧以邻接表为例)】
在这种类似于层次遍历的算法中,先访问的顶点,其邻接点也会被优先访问。因此,需要引入队列保存以被访问过的结点。
另外,该算法同样需要一个标志数组。
void BFS(ALGraph G, int v)
{cout << G.vertices[v].data; //访问第v个顶点,并且通过标志数组进行标记visited[v] = true;SqQueue Q;InitQueue(Q); //初始化队列QEnQueue(Q, v); //v进队while (!QueueEmpty(Q)) //若队列非空{int u = 0;DeQueue(Q, u); //弹出队头元素for (int w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w)){//依此检查u的所有邻接点if (!visited[w]) //若w是u未被访问的邻接点{cout << G.vertices[w].data;visited[w] = true; //访问,并置标记EnQueue(Q, w); //w进队}}}
}若为非连通图,则该算法也一定会有无法访问到的顶点。此时就需要另寻未被访问过的顶点,重复上述广度优先搜索过程:

这和深度优先算法很类似,仅需将DFS函数替换为BFS函数即可。
【算法分析:BFSTraverse函数】
因为每个顶点最多仅一次进入队列,故该算法实质上就是通过边寻找邻接点的过程。类似于深度优先算法,当使用邻接表存储时,该算法的时间复杂度为O(n + e)(同样的,若使用邻接矩阵存储,则时间复杂度为O(n²))。
相关文章:

数据结构入门6-1(图)
目录 注 图的定义 图的基本术语 图的类型定义 图的存储结构 邻接矩阵 1. 邻接矩阵表示法 2. 使用邻接矩阵表示法创建无向网 3. 邻接矩阵表示法的优缺点 邻接表 1. 邻接表表示法 2. 通过邻接表表示法创建无向图 3. 邻接表表示法的优缺点 十字链表(有向…...
把C#代码上传到NuGet,大佬竟是我自己!!!
背景 刚发表完一篇博客总结自己写标准化C#代码的心历路程,立马就产生一个问题,就是我写好标准化代码后,一直存放磁盘的话,随着年月增加,代码越来越多,项目和版本的管理就会成为一个令我十分头疼的难题&…...

解决前端“\n”不换行问题
在日常开发过程中,换行显示是一种很常见的应用需求,但是偶然发现,有时候使用 "\n"并不会换行显示,只会被识别为空格,如下图。 通过上图可以看出,"\n"它被识别成了一个空格显示&#…...
Python打包成exe,文件太大问题解决办法(比保姆级还保姆级)
首先我要说一下,如果你不在乎大小,此篇直接别看了,因为我写过直接打包的,就多20M而已,这篇就别看了,点击查看不在乎大小直接打包这篇我觉得简单的令人发指 不废话,照葫芦画瓢就好 第1步&#…...

CSS弹性布局flex属性整理
1.align-items align-items属性:指定弹性布局内垂直方向的对齐方向。 常用属性: center 垂直居中展示 flex-start 头部对齐 flex-end 底部对齐 2. justify-content justify-content属性:属性(水平)对齐弹…...

14个你需要知道的实用CSS技巧
让我们学习一些实用的 CSS 技巧,以提升我们的工作效率。这些 CSS 技巧将帮助我们开发人员快速高效地构建项目。 现在,让我们开始吧。 1.CSS :in-range 和 :out-of-range 伪类 这些伪类用于在指定范围限制之内和之外设置输入样式。 (a) : 在范围内 如…...

【Flutter从入门到入坑之四】构建Flutter界面的基石——Widget
【Flutter从入门到入坑】Flutter 知识体系 【Flutter从入门到入坑之一】Flutter 介绍及安装使用 【Flutter从入门到入坑之二】Dart语言基础概述 【Flutter从入门到入坑之三】Flutter 是如何工作的 WidgetWidget 是什么呢?Widget 渲染过程WidgetElementRenderObjectR…...
中职网络空间安全windows渗透
目录 B-1:Windows操作系统渗透测试 1.通过本地PC中渗透测试平台Kali对服务器场景Windows进行系统服务及版本扫描渗透测试,并将该操作显示结果中Telnet服务对应的端口号作为FLAG提交;编辑 2.通过本地PC中渗透测试平台Kali对服务器场景Wind…...
普通二叉树的操作
普通二叉树的操作1. 前情说明2. 二叉树的遍历2.1 前序、中序以及后序遍历2.1.1 前序遍历2.1.2 中序遍历、后序遍历2.2 题目练习2.2.1 求一棵二叉树的节点个数2.2.2 求一棵二叉树的叶节点个数2.2.3 求一棵二叉树第k层节点的个数2.2.4 求一棵二叉树的深度2.2.5 在一棵二叉树中查找…...

Oracle:递归树形结构查询功能
概要树状结构通常由根节点、父节点(PID)、子节点(ID)和叶节点组成。查询语法SELECT [LEVEL],* FROM table_name START WITH 条件1 CONNECT BY PRIOR 条件2 WHERE 条件3 ORDER BY 排序字段说明:LEVEL—伪列࿰…...

MongoDB数据库性能监控详解
目录一、MongoDB启动超慢1、启动日常卡住,根本不用为了截屏而快速操作,MongoDB启动真的超级慢~~2、启动MongoDB配置服务器,间歇性失败。3、查看MongoDB日志,分析“MongoDB启动慢”的原因。4、耗时“一小时”,MongoDB启…...

python不要再使用while死循环,使用定时器代替效果更佳!
在python开发的过程中,经常见到小伙伴直接使用while True的死循环sleep的方式来保存程序的一直运行。 这种方式虽然能达到效果,但是说不定什么时候就直接崩溃了。并且,在Linux环境中在检测到while True的未知进程就会直接干掉。 面对这样的…...
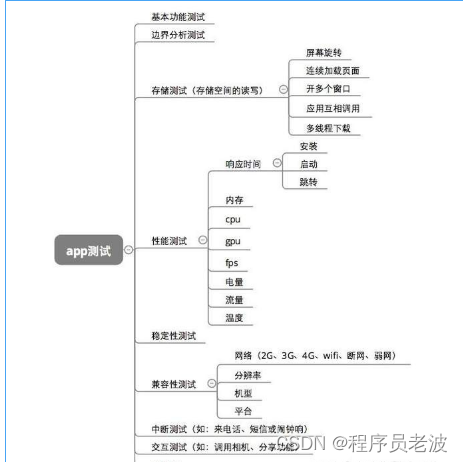
什么是接口测试?十年阿里测试人教你怎样做接口测试
一 什么是接口? 接口测试主要用于外部系统与系统之间以及内部各个子系统之间的交互点,定义特定的交互点,然后通过这些交互点来,通过一些特殊的规则也就是协议,来进行数据之间的交互。接口测试主要用于外部系统与系统之…...
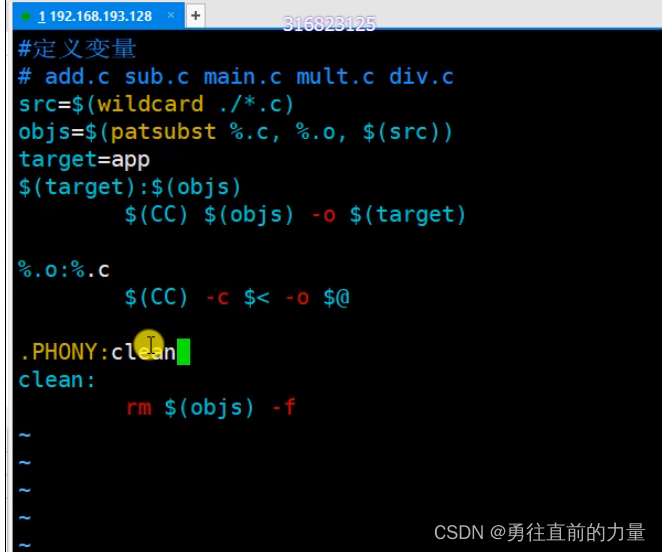
1.10-1.12 Makefile
1. Makefile简介 举个栗子,如下为redis-5.0.10的项目目录,有很多的文件 有了Makefile文件,可以简单的make一下就可以对项目文件进行编译,最终生成可执行程序。 2. Makefile栗子1 首先,创建vim Makefile按照PPT里的格…...
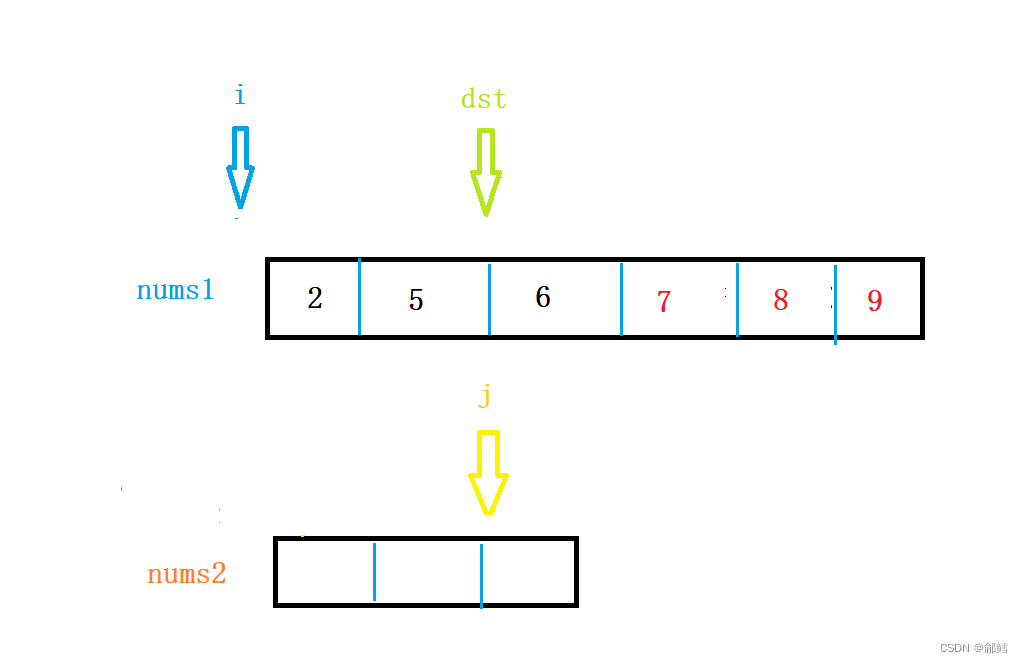
Leetcode. 88合并两个有序数组
合并两个有序数组 文章目录归并思路二归并 核心思路: 依次比较,取较小值放入新数组中 i 遍历nums1 , j 遍历nums2 ,取较小值放入nums3中 那如果nums[i] 和nums[j]中相等,随便放一个到nums3 那如果nums[i] 和nums[j]中相…...
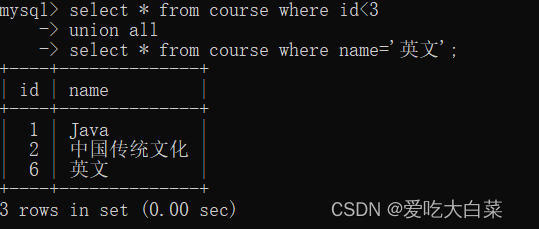
【数据库】数据库查询(进阶命令详解)
目录 1.聚合查询 1.1聚合函数 COUNT函数 SUM函数 AVG函数 MAX函数 MIN函数 1.2GROUP BY子句 1.3HAVING 2.联合查询 2.1内连接 2.2外连接 2.3自连接 2.4子查询 3.合并查询 写在前面: 文章截图均是每个代码显示的图。数据库对代码大小写不敏感&am…...

参数缺省和函数重载讲解
一路风雨兼程磨砺意志,三载苦乐同享铸就辉煌 目录 1.参数缺省的概念 2.参数缺省的用法 3.缺省参数分类 3.1.全缺省参数 3.2.半缺省参数 4.函数重载的概念 5.函数重载的用法 6.函数重载的原理 1.参数缺省的概念 一般情况下,函数调用时的实参个数应…...

关于召开2023第八届国际发酵培养基应用发展技术论坛的通知
生物发酵培养基是影响产业技术水平、环境友好程度的重要影响因素,为进一步实现生物发酵培养基的稳定可控、高效生产以及绿色安全,进一步推动生物技术的创新升级、绿色低碳循环生产,需要加强跨界联合,集中优势力量,突破…...
Java之深度优先(DFS)和广度优先(BFS)及相关题目
目录 一.深度优先遍历和广度优先遍历 1.深度优先遍历 2.广度优先遍历 二.图像渲染 1.题目描述 2.问题分析 3代码实现 1.广度优先遍历 2.深度优先遍历 三.岛屿的最大面积 1.题目描述 2.问题分析 3代码实现 1.广度优先遍历 2.深度优先遍历 四.岛屿的周长 1.题目描…...

【链表OJ题(四)】反转链表
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录链表OJ题(四)1. 反转…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
