简谈设计模式之建造者模式
建造者模式是一种创建型设计模式, 旨在将复杂对象的构建过程与其表示分离, 使同样的构建过程可以构建不同的表示. 建造者模式主要用于以下情况:
- 需要创建的对象非常复杂: 这个对象由多个部分组成, 且这些部分需要一步步地构建
- 不同的表示: 通过相同的构建过程可以生成不同的表示
- 构建过程的控制: 希望能够有更多的控制, 逐步创建对象, 而不是在一个步骤中完成
建造者模式结构
- 抽象建造者: 定义了创建产品的各部件的抽象接口
- 具体建造者: 实现了建造者接口, 构建并装配各个部件, 最终生成具体的产品
- 产品: 具体要创建的复杂对象
- 指挥者: 负责安排已有模块的顺序构建一个复杂的对象
建造者模式实现
// 产品类
public class Product {private String partA;private String partB;private String partC;public void setPartA(String partA) {this.partA = partA;}public void setPartB(String partB) {this.partB = partB;}public void setPartC(String partC) {this.partC = partC;}@Overridepublic String toString() {return "Product [partA=" + partA + ", partB=" + partB + ",partC=" + partC + "]";}
}// 抽象建造者
public abstract class Builder {protected Product product = new Product();public abstract void buildPartA();public abstract void buildPartB();public abstract void buildPartC();public Product getResult() {return product;}
}// 具体建造者
public class ConcreteBuilder extends Builder {@Overridepublic void buildPartA() {product.setPartA("Part A");}@Overridepublic void buildPartB() {product.setPartA("Part B");}@Overridepublic void buildPartC() {product.setPartA("Part C");}
}// 指挥者
public class Director {private Builder builder;public Director(Builder builder) {this.builder = builder}public void construct() {builder.buildPartA();builder.buildPartB();builder.buildPartC();}
}
优点:
- 易于拓展: 通过创建新的具体建造者, 可以很容易地增加新的产品表示
- 细粒度控制: 可以一步步地构建对象, 细化对象的创建流程
- 封装性: 将复杂对象的创建封装在建造者中, 客户端无需了解细节
缺点:
- 更多的代码量: 为了实现建造者模式, 需要更多的类和接口, 增加了代码量
- 复杂性: 对于简单的对象创建, 建造者模式过于复杂了
相关文章:

简谈设计模式之建造者模式
建造者模式是一种创建型设计模式, 旨在将复杂对象的构建过程与其表示分离, 使同样的构建过程可以构建不同的表示. 建造者模式主要用于以下情况: 需要创建的对象非常复杂: 这个对象由多个部分组成, 且这些部分需要一步步地构建不同的表示: 通过相同的构建过程可以生成不同的表示…...

力扣 hot100 -- 动态规划(下)
目录 💻最长递增子序列 AC 动态规划 AC 动态规划(贪心) 二分 🏠乘积最大子数组 AC 动规 AC 用 0 分割 🐬分割等和子集 AC 二维DP AC 一维DP ⚾最长有效括号 AC 栈 哨兵 💻最长递增子序列 300. 最长递增子序列…...
【计算机毕业设计】018基于weixin小程序实习记录
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

力扣之有序链表去重
删除链表中的重复元素,重复元素保留一个 p1 p2 1 -> 1 -> 2 -> 3 -> 3 -> null p1.val p2.val 那么删除 p2,注意 p1 此时保持不变 p1 p2 1 -> 2 -> 3 -> 3 -> null p1.val ! p2.val 那么 p1,p2 向后移动 p1 …...

Apache配置与应用(优化apache)
Apache配置解析(配置优化) Apache链接保持 KeepAlive:决定是否打开连接保持功能,后面接 OFF 表示关闭,接 ON 表示打开 KeepAliveTimeout:表示一次连接多次请求之间的最大间隔时间,即两次请求之间…...
怎么将3张照片合并成一张?这几种拼接方法很实用!
怎么将3张照片合并成一张?在我们丰富多彩的日常生活里,是否总爱捕捉那些稍纵即逝的美好瞬间,将它们定格为一张张珍贵的图片?然而,随着时间的推移,这些满载回忆的宝藏却可能逐渐演变成一项管理挑战ÿ…...
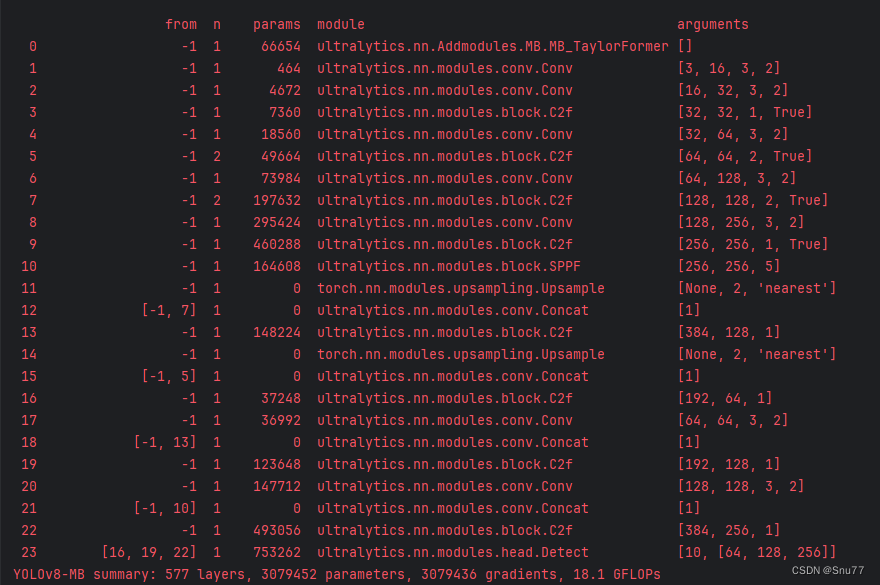
YOLOv10改进 | 图像去雾 | MB-TaylorFormer改善YOLOv10高分辨率和图像去雾检测(ICCV,全网独家首发)
一、本文介绍 本文给大家带来的改进机制是图像去雾MB-TaylorFormer,其发布于2023年的国际计算机视觉会议(ICCV)上,可以算是一遍比较权威的图像去雾网络, MB-TaylorFormer是一种为图像去雾设计的多分支高效Transformer…...
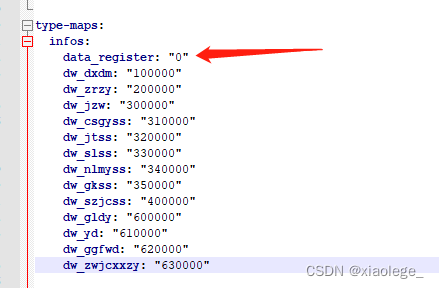
spring boot读取yml配置注意点记录
问题1:yml中配置的值加载到代码后值变了。 现场yml配置如下: type-maps:infos:data_register: 0ns_xzdy: 010000ns_zldy: 020000ns_yl: 030000ns_jzjz: 040000ns_ggglyggfwjz: 050000ns_syffyjz: 060000ns_gyjz: 070000ns_ccywljz: 080000ns_qtjz: 090…...

电子电气架构 --- 关于DoIP的一些闲思 下
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

Java getSuperclass和getGenericSuperclass
1.官方API对这两个方法的介绍 getSuperclass : 返回表示此 Class 所表示的实体(类、接口、基本类型或 void)的超类的 Class。如果此 Class 表示 Object 类、一个接口、一个基本类型或 void,则返回 null。如果此对象表示一个数组类ÿ…...

ARM功耗管理标准接口之ACPI
安全之安全(security)博客目录导读 思考:功耗管理有哪些标准接口?ACPI&PSCI&SCMI? Advanced Configuration and Power Interface Power State Coordination Interface System Control and Management Interface ACPI可以被理解为一…...

2024年网络监控软件排名|10大网络监控软件是哪些
网络安全,小到关系到企业的生死存亡,大到关系到国家的生死存亡。 因此网络安全刻不容缓,在这里推荐网络监控软件。 2024年这10款软件火爆监控市场。 1.安企神软件: 7天免费试用https://work.weixin.qq.com/ca/cawcde06a33907e6…...

通过Arcgis从逐月平均气温数据中提取并计算年平均气温
通过Arcgis快速将逐月平均气温数据生成年平均气温数据。本次用2020年逐月平均气温数据操作说明。 一、准备工作 (1)准备Arcmap桌面软件; (2)准备2020年逐月平均气温数据(NC格式)、范围图层数据&…...

每日一题~abc356(对于一串连续数字 找规律,开数值桶算贡献)
添加链接描述 题意:对于给定的n,m 。计算0~n 每一个数和m & 之后,得到的数 的二进制中 1的个数的和。 一位一位的算。最多是60位。 我们只需要计算 在 1-n这些数上,有多少个数 第i位 为1. 因为是连续的自然数,每一位上1 的…...

商业合作方案撰写指南:让你的提案脱颖而出的秘诀
作为一名策划人,撰写一份商业合作方案需要细致的规划和清晰的表达。 它是一个综合性的过程,需要策划人具备市场洞察力、分析能力和创意思维。 以下是能够帮助你撰写一份有效的商业合作方案的关键步骤和要点: 明确合作目标:设定…...

【MySQL】锁(黑马课程)
【MySQL】锁 0. 锁的考察点1. 概述1. 锁的分类1.1 属性分类1.2 粒度分类 2. 全局锁2.1 全局锁操作2.2.1 备份问题 3. 表级锁3.1 表锁3.2 语法3.3 表共享读锁(读锁)3.4 表独占写锁(写锁)3.5 元数据锁(meta data lock, MDL)3.6 意向…...
1.10编程基础之简单排序--02:奇数单增序列
OpenJudge - 02:奇数单增序列http://noi.openjudge.cn/ch0110/02/ 描述 给定一个长度为N(不大于500)的正整数序列,请将其中的所有奇数取出,并按升序输出。 输入 共2行: 第1行为 N; 第2行为 N 个正整数,其间用空格间隔。 输出 增序输出的奇数序列,数据之间以逗号间隔。数…...

【leetcode78-81贪心算法、技巧96-100】
贪心算法【78-81】 121.买卖股票的最佳时机 class Solution:def maxProfit(self, prices: List[int]) -> int:dp[[0,0] for _ in range(len(prices))] #dp[i][0]第i天持有股票,dp[i][1]第i天不持有股票dp[0][0] -prices[0]for i in range(1, len(prices)):dp[…...

IEC62056标准体系简介-4.IEC62056-53 COSEM应用层
为在通信介质中传输COSEM对象模型,IEC62056参照OSI参考模型,制定了简化的三层通信模型,包括应用层、数据链路层(或中间协议层)和物理层,如图6所示。COSEM应用层完成对COSEM对象的属性和方法的访问ÿ…...

嵌入式应用开发之代码整洁之道
前言:本系列教程旨在如何将自己的代码写的整洁,同时也希望小伙伴们懂如何把代码写脏,以备不时之需,同时本系列参考 正点原子 , C代码整洁之道,编写可读的代码艺术。 #好的代码的特点 好的代码应该都有着几…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
