maven 依赖冲突
依赖冲突
1、对于 Maven 而言,同一个 groupId 同一个 artifactId 下,只能使用一个 version。
<!-- https://mvnrepository.com/artifact/org.apache.commons/commons-math3 --><dependency><groupId>org.apache.commons</groupId><artifactId>commons-math3</artifactId><version>3.6.1</version></dependency><!-- 只会使用 3.6 这个版本的依赖 --><dependency><groupId>org.apache.commons</groupId><artifactId>commons-math3</artifactId><version>3.6</version></dependency>若相同类型但版本不同的依赖存在于同一个 pom 文件,只会引入后一个声明的依赖。

2、项目的两个依赖同时引入了某个依赖。
- 最短路径优先(Nearest Definition Wins):即优先选择依赖树中离项目最近的版本。
- 先声明者优先(First Declaration Wins):即优先选择在
pom.xml中首次声明的依赖版本。
举个例子,项目存在下面这样的依赖关系:
依赖链路一:A -> B -> C -> X(1.0)
依赖链路二:A -> D -> X(2.0)
这两条依赖路径上有两个版本的 X,为了避免依赖重复,Maven 只会选择其中的一个进行解析。
哪个版本的 X 会被 Maven 解析使用呢?
Maven 在遇到这种问题的时候,会遵循 路径最短优先 和 声明顺序优先 两大原则。解决这个问题的过程也被称为 Maven 依赖调解 。
最短路径优先:
依赖链路一:A -> B -> C -> X(1.0) // dist = 3
依赖链路二:A -> D -> X(2.0) // dist = 2
依赖链路二的路径最短,因此,X(2.0)会被解析使用。
不过,你也可以发现。路径最短优先原则并不是通用的,像下面这种路径长度相等的情况就不能单单通过其解决了:
先声明者优先:举个例子,项目存在下面这样的依赖关系:
依赖链路一:A -> B -> X(1.0)
依赖链路二:A -> D -> X(2.0)
这两条依赖路径上有两个版本的 X,为了避免依赖重复,Maven 只会选择其中的一个进行解析。
<!-- A pom.xml -->
<dependencies>...dependency B...dependency D
</dependencies>
在依赖路径长度相等的前提下,在 pom.xml 中依赖声明的顺序决定了谁会被解析使用,顺序最前的那个依赖优胜。该例中,如果 B 的依赖声明在 D 之前,那么 X (1.0)就会被解析使用。
排除依赖
单纯依赖 Maven 来进行依赖调解,在很多情况下是不适用的,需要我们手动排除依赖。
举个例子,当前项目存在下面这样的依赖关系:
依赖链路一:A -> B -> C -> X(1.5) // dist = 3
依赖链路二:A -> D -> X(1.0) // dist = 2
根据路径最短优先原则,X(1.0) 会被解析使用,也就是说实际用的是 1.0 版本的 X。
但是!这会一些问题:如果 D 依赖用到了 1.5 版本的 X 中才有的一个类,运行项目就会报NoClassDefFoundError错误。如果 D 依赖用到了 1.5 版本的 X 中才有的一个方法,运行项目就会报NoSuchMethodError错误。
现在知道为什么你的 Maven 项目总是会报NoClassDefFoundError和NoSuchMethodError错误了吧?
如何解决呢? 我们可以通过exclusion标签手动将 X(1.0) 给排除。
<dependency>......<exclusions><exclusion><artifactId>x</artifactId><groupId>org.apache.x</groupId></exclusion></exclusions>
</dependency>
一般在解决依赖冲突的时候,都会优先保留版本较高的。这是因为大部分 jar 在升级的时候都会做到向下兼容。
如果高版本修改了低版本的一些类或者方法的话,这个时候就能直接保留高版本了,而是应该考虑优化上层依赖,比如升级上层依赖的版本。
还是上面的例子:
依赖链路一:A -> B -> C -> X(1.5) // dist = 3
依赖链路二:A -> D -> X(1.0) // dist = 2
保留了 1.5 版本的 X,但是这个版本的 X 删除了 1.0 版本中的某些类。这个时候,可以考虑升级 D 的版本到一个 X 兼容的版本。
更多消息资讯,请访问昂焱数据。
相关文章:

maven 依赖冲突
依赖冲突 1、对于 Maven 而言,同一个 groupId 同一个 artifactId 下,只能使用一个 version。 <!-- https://mvnrepository.com/artifact/org.apache.commons/commons-math3 --><dependency><groupId>org.apache.commons</groupId&…...

demon drone 200无人机标定流程
demon drone 200无人机标定流程 一、飞控固件更新1.1 固件更新1.2 参数更新 二、imu标定2.1 安装imu标定工具(在你自己的电脑上)2.2 录制rosbag(在对应飞机上)2.3 运行标定程序(在你自己的电脑上) 三、双目及imu联合标定3.1 安装标…...

案例开发-日程管理-第一期
九 案例开发-日程管理-第一期 共7期 9.1 登录页及校验 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><style>.ht{text-align: center;color: cadetblue;font-family: 幼…...

【Java 注解,自定义注解,元注解,注解本质,注解解析】
文章目录 什么是注解?Java内置注解自定义注解元注解注解的本质注解解析 什么是注解? 注解是Java编程语言中的一种元数据,提供了有关程序的额外信息。注解以符号开始,紧跟着注解的名称和一对括号,括号内包含注解的参数…...

染色法判定二分图
什么是二分图? 二分图,也称作二部图,是图论中的一种特殊模型。在一个无向图G(V,E) 中,如果顶点集合 V 可以被分割成两个互不相交的子集 A 和 B,并且图中的每条边 (i,j) 关联的两个顶点 i 和 j 分别属于这两个不同的顶…...

自动气象站的主要功能优势
在科技日新月异的今天,我们生活的方方面面都受到了科技的影响。其中,自动气象站作为气象观测领域的重要一环,不仅提升了气象数据的准确性和时效性,还为我们的日常生活、农业生产、灾害预防等提供了重要的数据支持。 自动气象站概述…...

Java中实现二维数组(矩阵)的转置
在矩阵运算中,矩阵的转置是一个基本操作,即将矩阵的行变成列,列变成行。在Java中,我们可以通过编写一个方法来实现二维数组的转置。下面,我将详细介绍如何在Java中完成这一任务,并提供完整的代码示例。 编…...
Prometheus+Grafana主机运行数据
目录 介绍 安装Node Exporter 配置Prometheus 验证配置 导入仪表盘 介绍 Prometheus是一款开源的监控和警报工具,而Node Exporter是Prometheus的一个官方插件,用于采集主机上的各种系统和硬件指标。 安装Node Exporter 下载最新版本的Node Export…...

GraphQL在Postman中:释放API查询的强大潜能
🚀 GraphQL在Postman中:释放API查询的强大潜能 Postman作为API开发和测试的领先工具,对GraphQL的支持为开发者提供了一种新的方式来查询和管理数据。GraphQL是一种查询语言,用于API,允许客户端明确指定他们需要哪些数…...

大语言模型里的微调vs RAG vs 模板提示词
文章目录 介绍微调(Fine-tuning)定义优点:缺点:应用场景:技术细节 检索增强生成(RAG,Retrieval-Augmented Generation)定义优点:缺点:应用场景:技…...

网络编程:常用网络测试工具
telnet netstat ping arp wireshark(网络抓包工具) tcpdumpssh2 secure crt ——软件工具sudo ufw disable sudo apt-get install openssh-server openssh-client //两个命令敲完 得重启sudo apt-get install wireshark 1、telnet 远程登录工具&…...
mov视频怎么改成mp4?把mov改成MP4的四个方法
mov视频怎么改成mp4?选择合适的视频格式对于确保内容质量和流通性至关重要。尽管苹果公司的mov格式因其出色的视频表现备受赞誉,但在某些情况下,它并非最佳选择,因为使用mov格式可能面临一些挑战。MP4格式在各种设备(如…...

力扣1472.设计浏览器历史记录
力扣1472.设计浏览器历史记录 用双指针记录历史记录 以及栈顶高度移动时会直接把之前的记录消掉 class BrowserHistory {int pos-1;int top0;string history[5010];public:BrowserHistory(string homepage) {visit(homepage);}void visit(string url) {pos ;top pos;histor…...

准大一新生开学千万要带证件照用途大揭秘
1、提前关注好都有哪些考场,以及这些考场大致在网页的哪个位置。比如我选对外经贸大学,我就直接找到第二个点进去。 2、电脑上同时开了谷歌浏览器和IE浏览器,以及手机也登陆了。亲测下来,同一时间刷新,谷歌浏览器能显示…...

QImage显示图片像素
在Qt中,QImage 类是用来表示和处理图像的。如果你想查看或显示一个图片的像素数据,你可以使用 QImage 提供的方法来访问这些数据。以下是一些基本的方法来获取和显示图片的像素信息: 获取图像的像素格式: 使用 QImage::format() …...
uniapp使用高德地图(公众号+h5)
选择微信小程序的话后果就是你的地图出不来,出来了就报key异常 下面直接放配置和代码: 打包后的高德uni-app,uniCloud,serverless,高德地图,申请高德地图Key,配置使用高德地图,参数说明,高德开放平台用户名,百度地图,申请百度地图Key,配置使用百度地图,…...

深度学习与浅层学习:技术变革下的竞争态势
深度学习与浅层学习:技术变革下的竞争态势 在过去十年中,深度学习的崛起对整个人工智能领域产生了巨大影响,几乎在各种任务中显示出超越传统浅层学习方法的性能。这种变化不仅推动了技术的进步,还对硬件市场,尤其是显…...

LeetCode 219. 存在重复元素 II
LeetCode 219. 存在重复元素 II 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则,返回 false 。 示例 1&am…...

【目标检测】使用自己的数据集训练并预测yolov8模型
1、下载yolov8的官方代码 地址: GitHub - ultralytics/ultralytics: NEW - YOLOv8 🚀 in PyTorch > ONNX > OpenVINO > CoreML > TFLite 2、下载目标检测的训练权重 yolov8n.pt 将 yolov8n.pt 放在ultralytics文件夹下 3、数据集分布 注…...
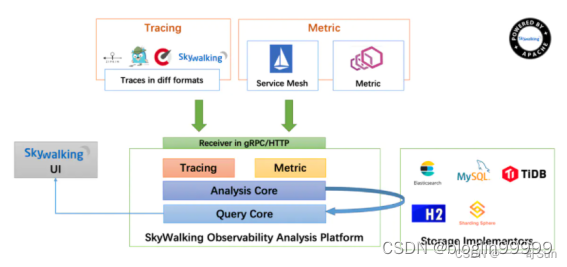
应用监控SkyWalking调研
参考: 链路追踪( Skyworking )_skywalking-CSDN博客 企业级监控项目Skywalking详细介绍,来看看呀-CSDN博客 SkyWalking 极简入门 | Apache SkyWalking 使用 SkyWalking 监控 ClickHouse Server | Apache SkyWalking https://zhuanlan.zhihu.com/p/3…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
