利用【Python】【线性规划】优化工厂生产:实现智能资源配置与利润最大化的现代解决方案
目录
1. 问题背景和描述
1.1 问题背景
1.2 问题描述
2. 数学模型的建立
2.1决策变量
2.2 目标函数
2.3 约束条件
2.4 数学模型总结
3. 使用Python解决线性规划问题
3.1 导入必要的库
3.2 定义目标函数系数
3.3 定义不等式约束矩阵和向量
3.4 定义变量的边界
非负约束
变量边界在SciPy中的表示
3.5 求解线性规划问题
调用linprog函数
3.6 输出结果
获取和解释最优解
4. 结果解释和应用
4.1 结果解释
4.2 应用
4.3 验证结果
5. 扩展阅读
5.1 扩展阅读
5.2 线性规划的其他类型
编辑
代码
结果
总结


专栏:数学建模学习笔记
1. 问题背景和描述
1.1 问题背景
在现代制造业和商业运作中,资源的有效利用和利润的最大化是企业追求的重要目标。企业面临的常见问题是如何在有限的资源条件下,通过合理分配和优化使用资源,来实现利润的最大化。线性规划(Linear Programming,LP)是一种数学优化技术,能够在这些情况下发挥重要作用。它通过建立数学模型,帮助企业在众多可能的选择中找到最优解,进而指导实际操作。
假设有一家工厂,生产两种产品:产品A和产品B。每种产品的生产都需要消耗特定的资源。每天,每种资源的使用时间是有限的,这使得资源分配问题变得复杂。工厂的目标是通过合理分配资源,确定每天应该生产多少单位的产品A和产品B,以实现总利润的最大化。
具体数据如下:
- 资源1:每天最多可用60个小时
- 资源2:每天最多可用40个小时
- 产品A:每单位需要资源1的2个小时和资源2的1个小时
- 产品B:每单位需要资源1的1个小时和资源2的2个小时
- 产品A:每单位的利润为30美元
- 产品B:每单位的利润为20美元
通过对这些数据进行分析和建模,我们可以利用线性规划技术来制定一个优化的生产计划,确保在资源限制条件下实现利润的最大化。
1.2 问题描述
我们需要建立一个线性规划模型来描述上述问题,并使用该模型找到每天应该生产的产品A和产品B的最优数量,从而实现总利润的最大化。同时,生产过程中必须满足资源的限制条件,即不能超过每天可用的资源时间。
在这个问题中,我们的目标是构建一个数学模型,通过这个模型可以:
- 确定每天生产的产品A和产品B的数量。
- 满足资源的限制条件。
- 实现总利润的最大化。
2. 数学模型的建立
建立数学模型是解决线性规划问题的基础。我们将根据问题背景中的具体数据,定义决策变量,构建目标函数和约束条件。
2.1决策变量
决策变量是我们希望通过优化确定的数量。在这个问题中,决策变量是每天生产的产品A和产品B的数量。我们定义两个决策变量:
- x1:每天生产的产品A的单位数量
- x2:每天生产的产品B的单位数量
这些决策变量将用于构建目标函数和约束条件。
2.2 目标函数
目标函数是我们希望优化的表达式。在这个问题中,目标是最大化总利润。总利润可以表示为生产的产品A和产品B的利润之和。具体来说:
- 产品A每单位的利润为30美元
- 产品B每单位的利润为20美元
因此,总利润可以表示为: 利润=30x1+20x2
我们的目标是最大化总利润,因此目标函数可以表示为: 最大化 z=30x1+20x2
2.3 约束条件
约束条件是模型中必须满足的限制。在这个问题中,约束条件包括资源的限制和生产数量的非负性。
资源1的限制: 2*x1+x2≤60
资源2的限制:x1+2*x2≤40
非负约束:x1≥0 ,x2≥0
这些约束条件确保生产计划不会超过可用的资源,并且生产的数量是非负的,即实际可行的。
2.4 数学模型总结
综合以上信息,我们可以建立一个完整的线性规划模型来描述这个问题。模型的形式如下:

3. 使用Python解决线性规划问题
在建立了数学模型之后,我们可以使用Python中的SciPy库来求解这个线性规划问题。SciPy库提供了许多优化算法,其中linprog函数可以用于求解线性规划问题。
3.1 导入必要的库
首先,我们需要导入必要的库:
import numpy as np
from scipy.optimize import linprog
3.2 定义目标函数系数
在求解问题时,SciPy的linprog函数默认是用于最小化问题的。因此,我们需要将最大化问题转换为最小化问题。具体来说,我们可以将目标函数的系数取负。
目标函数的系数为:c=[−30,−20]
在Python中定义目标函数系数:
c = [-30, -20]
3.3 定义不等式约束矩阵和向量

在Python中,我们可以定义约束矩阵和向量如下:
A = [[2, 1], [1, 2]]
b = [60, 40]
这里,A 是一个二维数组,表示约束条件的系数矩阵,每一行对应一个不等式约束条件,每一列对应一个决策变量。b 是一个一维数组,表示每个约束条件的右端常数项。
- 矩阵 A:每一行代表一个约束条件,每一列代表一个决策变量。在我们的例子中,第一行 [2, 1] 表示第一个约束条件 2x1+x2≤60,第二行 [1, 2] 表示第二个约束条件x1+2x2≤40。
- 向量 b:每个元素表示一个约束条件的右端常数项。对于我们的例子,向量 b 中的元素分别是 60 和 40,对应两个约束条件的右端值。
3.4 定义变量的边界
在实际的生产问题中,变量的取值范围通常是有限制的。对于我们的例子,每天生产的产品数量不能为负,因此我们需要设置变量的边界条件。
非负约束
线性规划问题中的非负约束是指决策变量必须是非负数,即:
x1≥0 x2≥0
这些非负约束条件确保了我们的生产数量是合理的(即,不能生产负数的产品)。
变量边界在SciPy中的表示
在SciPy的linprog函数中,变量的边界可以通过bounds参数来指定。每个决策变量的边界条件可以用一个元组表示,元组的第一个元素是变量的下界,第二个元素是变量的上界。如果变量没有上界,可以用None表示。
x_bounds = [(0, None), (0, None)]
这里,(0, None) 表示变量的下界是0,上界没有限制,即变量必须是非负的。
- 变量边界定义:我们用一个列表来表示每个变量的边界。列表中的每个元素是一个元组,元组的第一个元素表示变量的下界,第二个元素表示变量的上界。在我们的例子中,我们定义了两个变量 x1 和 x2,它们的边界条件都是非负的,因此我们用
(0, None)来表示它们的边界。- 意义和应用:非负约束条件确保了我们的生产计划是现实可行的,因为生产的数量不能为负数。这在实际应用中是非常重要的,可以防止在优化过程中出现不合理的解。
3.5 求解线性规划问题
在定义了目标函数的系数、约束条件和变量的边界之后,我们可以使用SciPy的linprog函数来求解这个线性规划问题。linprog函数是SciPy库中用于求解线性规划问题的主要函数。
调用linprog函数
linprog函数的基本调用方式如下:
res = linprog(c, A_ub=A, b_ub=b, bounds=x_bounds, method='highs')
其中:
c:目标函数的系数向量A_ub:不等式约束条件的系数矩阵b_ub:不等式约束条件的右端常数项向量bounds:变量的边界条件method:求解方法,这里我们使用highs方法,这是SciPy推荐的高效求解方法之一
- 目标函数的系数向量
c:之前定义的目标函数的系数向量[-30, -20]。注意这里我们将最大化问题转换为最小化问题,因此系数取负。- 不等式约束条件的系数矩阵
A_ub:定义了每个约束条件的系数矩阵[[2, 1], [1, 2]]。- 不等式约束条件的右端常数项向量
b_ub:对应于不等式约束的右端常数项向量[60, 40]。- 变量的边界条件
bounds:定义了变量的取值范围,确保变量是非负的。- 求解方法
method:指定使用highs方法,这是SciPy中一个高效的线性规划求解器。
3.6 输出结果
在求解完成之后,我们需要输出结果。结果对象res包含了优化的详细信息,包括最优解和最优目标函数值。
获取和解释最优解
最优解是指在满足所有约束条件的情况下,使目标函数达到最优值的决策变量值。在我们的例子中,最优解是每天应该生产的产品A和产品B的数量。
print('Optimal value:', round(res.fun * -1, ndigits=2)) # 恢复最大化问题的目标函数值
print('x:', res.x)
这里,res.fun 是最优目标函数值,因为我们最初将目标函数系数取了负,所以需要乘以-1来恢复最大化问题的目标函数值。res.x 是最优解,即最优的 x1 和 x2 的值。
4. 结果解释和应用
在得到线性规划问题的求解结果之后,我们需要对结果进行解释和应用。最优解和最优目标函数值对于实际的生产计划具有重要的指导意义。
4.1 结果解释
- 最优目标函数值:1400。这个值表示在满足所有资源约束的情况下,最大化的总利润为1400美元。
- 最优解:每天生产20个单位的产品A和10个单位的产品B。这是指在所有约束条件下能够使总利润最大化的最优生产计划。
4.2 应用
最优解对于工厂的生产计划具有重要的指导意义。通过按照最优解安排生产,工厂可以确保资源的有效利用,最大化利润。
具体来说,工厂应该每天生产20个单位的产品A和10个单位的产品B。这将使得总利润最大化,同时不超过每天可用的资源限制。通过这种方式,工厂可以实现资源的最佳配置,提高生产效率和经济效益。
4.3 验证结果
为了验证结果的正确性,我们可以检查最优解是否满足所有约束条件:
资源1的使用情况: 2×20+1×10=40+10=50≤60
资源2的使用情况: 1×20+2×10=20+20=40≤40
可以看到,最优解不仅最大化了总利润,而且满足所有约束条件。这表明我们的线性规划模型和求解过程是正确的,求解结果是合理的。
5. 扩展阅读
5.1 扩展阅读
线性规划问题在实际中有很多应用,如物流运输、生产计划、资源分配等。除了SciPy,其他常用的优化库还包括PuLP和Gurobi。
- PuLP:PuLP是一个开源的线性规划工具,可以与各种求解器结合使用。它提供了简单易用的接口,适合用于教学和简单的优化问题。
- Gurobi:Gurobi是一款高效的商业优化软件,支持求解线性规划、整数规划和其他优化问题。它具有强大的求解能力,适用于大规模和复杂的优化问题。
5.2 线性规划的其他类型
-
多目标优化:多目标优化考虑多个目标函数同时进行优化。例如,一个工厂可能希望在最大化利润的同时最小化污染物排放。多目标优化可以通过加权求和法或Pareto最优解来解决。
-
带有等式约束的线性规划:在约束条件中包含等式约束。例如,某些资源的使用量必须精确等于特定值。等式约束可以用于表示这些严格的资源限制或平衡条件。
-
混合整数线性规划:决策变量不仅包括连续变量,还包括整数变量。例如,在生产计划中,某些产品的生产数量必须为整数。混合整数线性规划可以通过将部分决策变量定义为整数来解决这些问题。
代码
import numpy as np
from scipy.optimize import linprog# 定义目标函数系数
# 我们希望最大化 30x1 + 20x2
# 在使用 linprog 时,我们需要将这个目标函数转化为最小化问题
# 因此我们取负,变为最小化 -30x1 - 20x2
c = [-30, -20]# 定义不等式约束矩阵和向量
# 不等式约束如下:
# 2x1 + x2 <= 60
# x1 + 2x2 <= 40
# 转化为矩阵形式 A @ x <= b
A = [[2, 1], [1, 2]]
b = [60, 40]# 定义变量的边界
# x1 >= 0
# x2 >= 0
x_bounds = [(0, None), (0, None)]# 使用 linprog 函数求解线性规划问题
res = linprog(c, A_ub=A, b_ub=b, bounds=x_bounds, method='highs')# 输出结果
print('Optimal value:', round(res.fun * -1, ndigits=2)) # 恢复最大化问题的目标函数值
print('x:', res.x)# 结果解释
# 最优目标函数值
optimal_value = round(res.fun * -1, ndigits=2)
# 最优解
optimal_solution = res.xprint(f"在满足资源约束的情况下,最大化的总利润为:{optimal_value} 美元")
print(f"每天生产 {optimal_solution[0]} 个单位的产品A 和 {optimal_solution[1]} 个单位的产品B")# 验证结果是否满足所有约束条件
# 资源1的使用情况
resource1_usage = 2 * optimal_solution[0] + optimal_solution[1]
# 资源2的使用情况
resource2_usage = optimal_solution[0] + 2 * optimal_solution[1]print(f"资源1的使用情况:{resource1_usage} 小时(<= 60 小时)")
print(f"资源2的使用情况:{resource2_usage} 小时(<= 40 小时)")# 验证是否满足所有约束条件
if resource1_usage <= 60 and resource2_usage <= 40:print("最优解满足所有约束条件。")
else:print("最优解不满足所有约束条件。")
结果

总结
建立线性规划模型,以解决生产优化问题。通过定义决策变量、目标函数和约束条件,使用Python的SciPy库中的linprog函数求解模型,并验证结果的合理性。最终,确定了在资源限制条件下最大化利润的最优生产方案.
相关文章:

利用【Python】【线性规划】优化工厂生产:实现智能资源配置与利润最大化的现代解决方案
目录 1. 问题背景和描述 1.1 问题背景 1.2 问题描述 2. 数学模型的建立 2.1决策变量 2.2 目标函数 2.3 约束条件 2.4 数学模型总结 3. 使用Python解决线性规划问题 3.1 导入必要的库 3.2 定义目标函数系数 3.3 定义不等式约束矩阵和向量 3.4 定义变量的边界 非负…...

【spark】Exception in thread “main“ ExitCodeException exitCode=-1073741701
在window上运行spark程序写到本地文件的时候报错。 val rdd sc.sparkContext.parallelize(list)val arr rdd.collect()arr.foreach(println)rdd.saveAsTextFile("test1")sc.close()错误信息: zhangsan lisi wangwu Exception in thread "main" ExitCode…...

数学建模美赛经验小结
图片资料来自网络所听讲座,感谢分享!...
)
206. 反转链表 (Swift 版本)
题目 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 解题 /*** Definition for singly-linked list.* public class ListNode {* public var val: Int* public var next: ListNode?* public init() { self.val 0; self.…...

海狐外卖O2O商城系统:技术架构与运营模式的深度解析
摘要: 本文深入探讨了海狐外卖O2O商城系统的技术架构、功能特性以及运营模式。海狐外卖作为一款专注于细分市场领域的外卖餐饮解决方案,不仅拥有先进的技术栈支持,还通过丰富的系统插件和灵活的运营模式,为商户和用户提供高效、便…...

14-31 剑和诗人5 - 使用 AirLLM 和分层推理在单个 4GB GPU 上运行 LLama 3 70B
利用分层推理实现大模型语言(LLM) 大型语言模型 (LLM) 领域最近取得了显著进展,LLaMa 3 70B 等模型突破了之前认为可能实现的极限。然而,这些模型的庞大规模给其部署和实际使用带来了巨大挑战,尤其是在资源受限的设备上,例如内存…...

风景园林工程设计乙级资质业绩要求案例分析
项目数量与规模 数量要求:企业需要提供一定数量的已完成风景园林设计项目案例,这个数量可能依据具体政策而有所不同,但通常需要完成多个项目以展示设计团队的综合能力。 规模要求:项目规模需达到乙级资质标准所规定的级别&#…...

无人机之飞行规划与管理篇
无人机飞行规划与管理是确保无人机安全、高效且符合法规的运行的关键步骤。这一过程包括了对飞行任务的详细安排、航线的设定以及风险的评估和管理。下面简述这一过程的主要环节: 一、飞行目的和任务确定 在规划之初,必须明确无人机的飞行目的…...

realsense D435l+mid360标定
目录 一、安装realsense环境 二、获取realsense D450L相机内参 三、标定雷达和相机 1.下载livox_camera_calib 2.修改配置参数 3.使用fastlio生成点云 4.标定 一、安装realsense环境 git clone https://github.com/IntelRealSense/librealsense.git cd librealsense //更…...

深度学习中的正则化技术 - 数据集增强篇
序言 在机器学习与深度学习的广阔领域中,数据集的质量与规模往往是决定模型性能的关键因素之一。然而,现实世界中高质量、标注完善的数据集往往稀缺且获取成本高昂,这成为了制约算法进步的一大瓶颈。为了缓解这一问题,数据集增强…...

【Docker系列】Docker 镜像源:优化你的容器化开发流程
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
【Linux】Windows环境下配置虚拟机静态IP
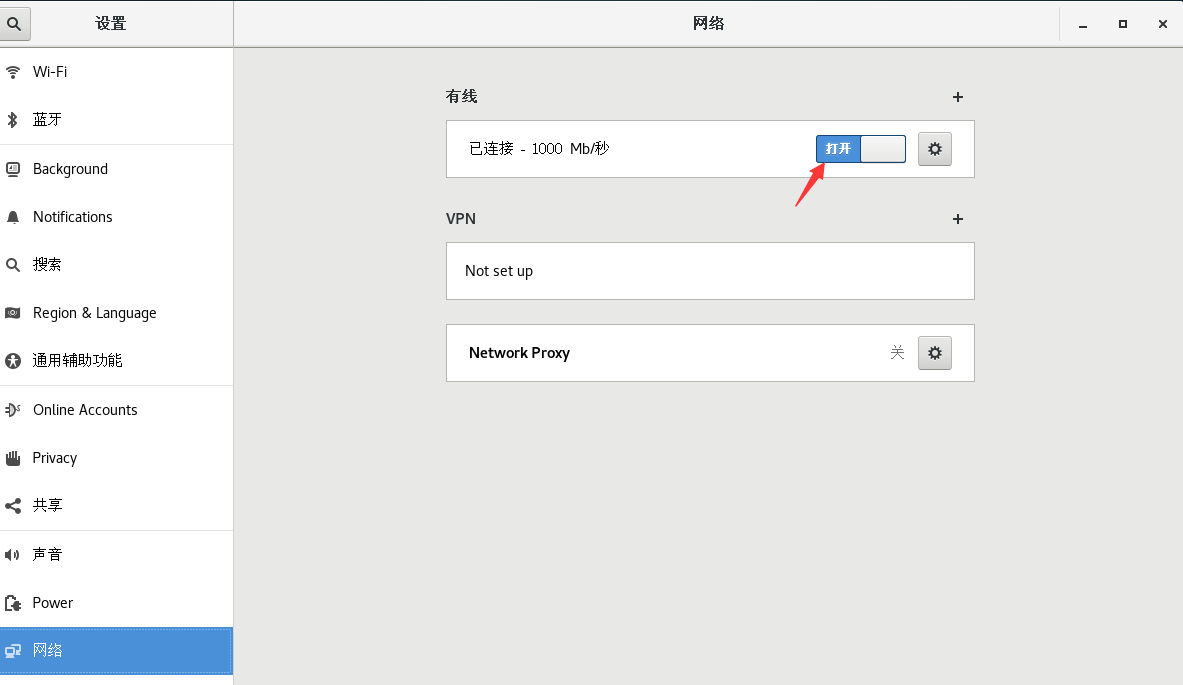
当前我们虚拟机的Linux操作系统,其IP地址是通过DHCP服务获取的。 DHCP:动态获取IP地址,即每闪重启设备后都会获取一次,可能导致IP地址频繁变更 原因1:办公电脑IP地址变化无所谓,但是我们要远程连接到Linux系统&#x…...

完美解决AttributeError: ‘list‘ object has no attribute ‘shape‘的正确解决方法,亲测有效!!!
完美解决AttributeError: ‘list‘ object has no attribute ‘shape‘的正确解决方法,亲测有效!!! 亲测有效 完美解决AttributeError: ‘list‘ object has no attribute ‘shape‘的正确解决方法,亲测有效࿰…...
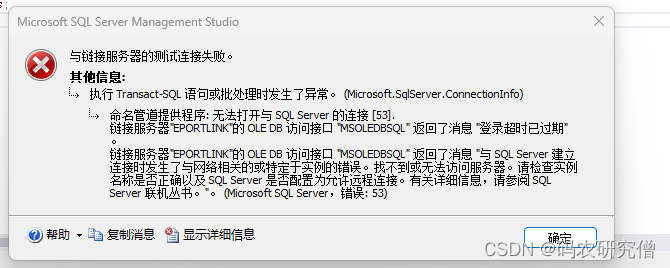
链接服务器“XX”的OLEDB访问接口“MSOLEDBSQL”返回了消息“登录超时已过期” 解决方法
目录 1. 问题所示2. 原理分析3. 解决方法1. 问题所示 出现如下问题: 与链接服务器的测试连接失败。执行Transact-SQL 语句或批处理时发生了异常。命名管道提供程序:无法打开与SQL SERVER的链接[53]链接服务器“XX”的OLEDB访问接口“MSOLEDBSQL”返回了消息“登录超时已过期…...

【AI伦理与社会责任】讨论人工智能在隐私保护、偏见消除、自动化对就业的影响等伦理和社会问题。
人工智能(AI)作为第四次产业革命的核心技术,在推动社会进步和经济发展的同时,也引发了一系列伦理和社会问题。以下从隐私保护、偏见消除以及自动化对就业的影响三个方面进行详细讨论。 一、隐私保护 人工智能技术的广泛应用涉及…...
TCP缓存区数据读取)
Qt编程技巧小知识点(1)TCP缓存区数据读取
文章目录 Qt编程技巧小知识点(1)TCP缓存区数据读取小结 Qt编程技巧小知识点(1)TCP缓存区数据读取 TCP的socket对内存进行读取(使用socket->readall())的时候输出的内容有时会进行局部倒置,其…...

vue 搭建 pinia
文章目录 环境设置存储读取数据【 storeToRefs】借助storeToRefs将store中的数据转为ref对象,方便在模板中使用【getters】当state中的数据,需要经过处理后再使用时,可以使用getters配置【$subscribe】通过 store 的 $subscribe() 方法侦听 s…...

什么是CLR
CLR,全称为Common Language Runtime,即公共语言运行时,是微软为.NET产品构建的运行环境,与Java的JVM(Java虚拟机)类似,可以看作是.NET的虚拟机。CLR的主要作用和特点如下: 主要作用…...

Spring MVC -01
Spring 的 MVC 框架 Spring的MVC框架是Spring框架的一部分,它提供了用于开发Web应用程序的一组组件和设计模式。MVC是Model-View-Controller的缩写,是一种设计模式,用于将应用程序的逻辑与用户界面分离。 在Spring的MVC框架中,Mo…...

山海鲸可视化——天地图画面和热力图
山海鲸引入天地图目前只有 iframe 的方式引入 首先我们创建一个文件夹 ——index.html ——index.js ——data.js 大家都是大佬,我就不详细介绍了,上代码都能看得懂 首先是index.html <!DOCTYPE html> <html lang"zh-CN"> <…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

