Python精神病算法和自我认知异类数学模型
🎯要点
🎯空间不确定性和动态相互作用自我认知异类模型 | 🎯精神病神经元算法推理 | 🎯集体信念催化个人行动力数学模型 | 🎯物种基因进化关系网络算法 | 🎯电路噪声低功耗容错解码算法
📜和-积消息传递算法用例
📜MATLAB激光通信和-积消息传递算法(Python图形模型算法)模拟调制
🍪语言内容分比


🍇Python贝叶斯网络消息传递算法
首先,假设我们有一个多叉树,它是没有循环的图。例如,我们有 4 个变量“下雨”、“洒水器”、“福尔摩斯”和“华生”,有向边分别为“下雨”到“福尔摩斯”、“下雨”到“华生”和“洒水器”到“福尔摩斯”。贝叶斯网络模拟了福尔摩斯和华生是邻居的故事。一天早上,福尔摩斯走出家门,发现草地湿了。要么是下雨了,要么是他忘了关洒水器。于是他去找邻居华生,看看他的草地是否也湿了。当他看到草地确实湿了时,他很确定他没有忘了洒水器,而是下雨了。因此,信息从华生流向洒水器。这种信息流由贝叶斯网络中的消息传递算法建模。
可能性包含有关观察的信息,例如,福尔摩斯草地在未观察的情况下的可能性为 1(湿)和 1(不湿)。如果观察到湿草,可能性变为 1(湿)和 0(不湿)。这些单位向量未归一化。
L ( X ) = ∏ K λ ( K → X ) L(X)=\prod_K \lambda_{(K \rightarrow X)} L(X)=K∏λ(K→X)
似然函数基本上是变量子级发送的所有传入消息的乘积。它返回一个似然向量,其中包含变量每个可能值的似然值。对于“下雨”,它的基数为 2,代表“是”和“否”两种状态。
如果某个变量没有子节点(因为它是图中的叶节点且未被观察到),则其似然向量将是一个单位向量,其所有可能值均为 1,例如,由于我们一开始没有观察到福尔摩斯的草,因此我们将其似然向量分别设置为 [1, 1],代表“不湿”和“湿”。
Python伪码表示:
def likelihood(self):incoming_children_messages = np.array([c.message_to_parent(self) for c in self.children])return incoming_children_messages.prod(axis=0)
先验是某些事件在开始时就已经知道的概率,例如,下雨的概率为 20%。如果先验未知,则使用以下公式进行计算。先验会给出相应变量的无条件概率。因此,我们还需要包括条件概率。
π ( X ) = ∑ W P ( X ∣ W ) ∏ K ϕ ( K → X ) \pi(X)=\sum_W P(X \mid W) \prod_K \phi_{(K \rightarrow X)} π(X)=W∑P(X∣W)K∏ϕ(K→X)
我们的例子中还给出了条件概率。公式中的“P(X|W)”对应于此。此外,我们需要使用来自所有父方的传入消息,即公式中的“ϕ”。索引显示消息方向 - 从父“K”到当前变量“X”。使用这两个部分(条件概率和来自父的消息)是因为它们都提供有关变量概率的信息。一方面,我们看到给定某些父值的概率,另一方面我们看到这些父的消息。如果没有观察,这些信息对应于父的先验。因此,这里计算“X”的边际并摆脱条件变量。
Python伪码表示:
def priors(self):parents_messages = [p.message_to_child(self) for p in self.parents]return reduce(np.dot, [self.m.transpose()]+parents_messages)
信念是我们观察到某些事件后的后验概率。它基本上是可能性和先验的标准化产物。
β ( X ) = α L ( X ) π ( X ) \beta(X)=\alpha L(X) \pi(X) β(X)=αL(X)π(X)
Python伪码表示:
def belief(self):unnormalized = self.likelihood() * self.priors()normalized = unnormalized/unnormalized.sum()return normalized
为了计算变量的可能性,我们需要考虑来自变量子项的所有传入消息,这些消息由似然函数中的 lambda 表示。
λ ( X → K ) = ∑ x ∈ X L ( x ) ∑ k ∈ K ; k ∈ u P ( x ∣ u ) ∏ i ≠ k ϕ ( Y → X ) i \lambda_{(X \rightarrow K)}=\sum_{x \in X} L(x) \sum_{k \in K ; k \in u} P(x \mid u) \prod_{i \neq k} \phi_{(Y \rightarrow X) i} λ(X→K)=x∈X∑L(x)k∈K;k∈u∑P(x∣u)i=k∏ϕ(Y→X)i
这个公式相当混乱,但看一些 Python 代码会更容易理解。一般来说,我们从 P(X|U) 中边缘化 K,而 X 是发送者(子节点),K 是接收者(父节点),U 是 X 的所有父节点,包括 K。如果我们想象一个 X 的条件概率表,对于每个条目,我们取父节点的相应激活,并将相应的传入消息 ϕ 乘以不包含 K 本身的数值。然后,我们将该值乘以 X 的似然值。最后,我们将所有 K 值相同的值相加,剩下向量是从 X 到 K 的消息。
Python伪码表示:
def message_to_parent(self, parent):likelihood = self.likelihood()parents_priors = np.array([p.message_to_child(self) for p in self.parents if p != parent])parent_i = self.parents.index(parent)stack = np.vstack([np.dot(self.m.take(r, axis=parent_i).transpose(), parents_priors.prod(axis=0)) for r in range(parent.cardinality)])return np.dot(stack, likelihood)
计算父方发送给子方的消息有两种方法。要么将从其他子方收到的所有消息与当前节点的先验相乘,要么将当前节点的信念除以相应子方发送给父方的消息。
κ ( X → K ) = α ∏ C \ K λ ( C → X ) π ( X ) = α β ( X ) λ ( K → X ) \kappa_{(X \rightarrow K)}=\alpha \prod_{C \backslash K} \lambda_{(C \rightarrow X)} \pi(X)=\alpha \frac{\beta(X)}{\lambda_{(K \rightarrow X)}} κ(X→K)=αC\K∏λ(C→X)π(X)=αλ(K→X)β(X)
我们认为这个公式称为 Kappa,其索引告诉我们消息的方向(从 X 到 K)。
如果我们看一下信念公式,就会发现这个公式是似然值和先验值的乘积。然而,似然值是所有传入消息的乘积。因此,信念除以来自 K 的传入消息,结果是所有传入消息(除了我们除以的消息)与先验值的乘积。这样,我们就可以解释两种计算 Kappa 的方法之间的相等性。给子方发送消息背后的直觉与给父方发送消息类似。您要考虑所有传入消息,然后将聚合发送到下一个节点。
Python伪码表示:
def message_to_child(self, child):children_messages = []for c in self.children:if c != child:children_messages.append(c.message_to_parent(self))if len(children_messages) > 0:unnormalized = (children_messages * self.get_priors())unnormalized = unnormalized.prod(axis=0)message = unnormalized/unnormalized.sum()return messagereturn self.get_priors()
👉参阅&更新:计算思维 | 亚图跨际
相关文章:

Python精神病算法和自我认知异类数学模型
🎯要点 🎯空间不确定性和动态相互作用自我认知异类模型 | 🎯精神病神经元算法推理 | 🎯集体信念催化个人行动力数学模型 | 🎯物种基因进化关系网络算法 | 🎯电路噪声低功耗容错解码算法 📜和-…...

npm install 报错:PhantomJS not found on PATH
npm install 报错:PhantomJS not found on PATH 整体报错内容 npm ERR! code 1 npm ERR! path G:\work-learn\open-coding\bruno\node_modules\phantomjs-prebuilt npm ERR! command failed npm ERR! command C:\Windows\system32\cmd.exe /d /s /c node install.…...

【C++进阶学习】第六弹——set和map——体会用C++来构建二叉搜索树
set和map基础:【C进阶学习】第五弹——二叉搜索树——二叉树进阶及set和map的铺垫-CSDN博客 前言: 在上篇的学习中,我们已经学习了如何使用C语言来实现二叉搜索树,在C中,我们是有现成的封装好的类模板来实现二叉搜索树…...

sqlmap确定目标/实操
安装kali,kali自带sqlmap,在window系统中跟linux系统操作有区别 sqlmap是一款自动化SQL工具,打开kali终端,输入sqlmap,出现以下界面,就说明sqlmap可用。 sqlmap确定目标 一、sqlmap直连数据库 1、直连数据库…...

Java笔试|面试 —— 对多态性的理解
谈谈对多态性的理解: 一个事物的多种形态(编译和运行时状态不一致性) 实现机制:通过继承、重写和向上转型(Object obj new 子类())来实现。 1.广义上的理解 子类对象的多态性,方法的重写&am…...
从RL的专业角度解惑 instruct GPT的目标函数
作为早期chatGPT背后的核心技术,instruct GPT一直被业界奉为里程碑式的著作。但是这篇论文关于RL的部分确写的非常模糊,几乎一笔带过。当我们去仔细审查它的目标函数的时候,心中不免有诸多困惑。特别是作者提到用PPO来做强化学习,…...

location匹配的优先级和重定向
nginx的重定向(rewrite) location 匹配 location匹配的就是后面的uri /wordpress 192.168.233.10/wordpress location匹配的分类和优先级 1.精确匹配 location / 对字符串进行完全匹配,必须完全符合 2.正则匹配 ^-前缀级别ÿ…...

观察矩阵(View Matrix)、投影矩阵(Projection Matrix)、视口矩阵(Window Matrix)及VPM矩阵及它们之间的关系
V表示摄像机的观察矩阵(View Matrix),它的作用是把对象从世界坐标系变换到摄像机坐标系。因此,对于世界坐标系下的坐标值worldCoord(x0, y0, z0),如果希望使用观察矩阵VM将其变换为摄像机坐标系下的坐标值localCoord(x…...

谷粒商城学习笔记-19-快速开发-逆向生成所有微服务基本CRUD代码
文章目录 一,使用逆向工程步骤梳理1,修改逆向工程的application.yml配置2,修改逆向工程的generator.properties配置3,以Debug模式启动逆向工程4,使用逆向工程生成代码5,整合生成的代码到对应的模块中 二&am…...
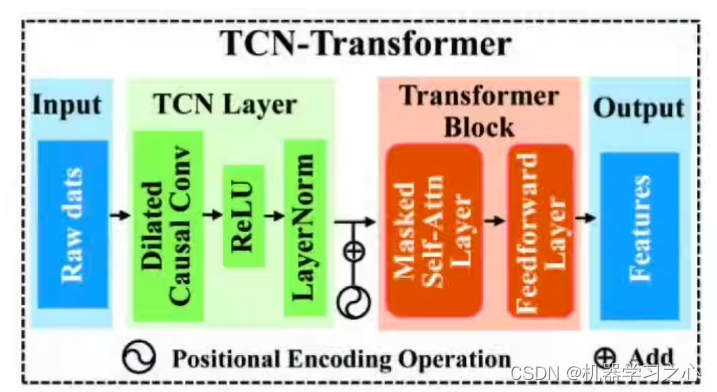
时序预测 | Matlab实现TCN-Transformer的时间序列预测
时序预测 | Matlab实现TCN-Transformer的时间序列预测 目录 时序预测 | Matlab实现TCN-Transformer的时间序列预测效果一览基本介绍程序设计 效果一览 基本介绍 基于TCN-Transformer模型的时间序列预测,可以用于做光伏发电功率预测,风速预测,…...
没想到MySQL 9.0这么拉胯
MySQL 7月1号发布了9.0版本,然而没想到并没有引起大家的狂欢,反而是来自DBA圈子的一篇吐槽,尤其是PG界吐槽更厉害。 难道MySQL现在真的这么拉胯了?本着好奇的态度,我也去下载了MySQL9.0的手册看了一下。确实有点让我大…...

开源 Wiki 系统 InfoSphere 2024.01.1 发布
推荐一套基于 SpringBoot 开发的简单、易用的开源权限管理平台,建议下载使用: https://github.com/devlive-community/authx 推荐一套为 Java 开发人员提供方便易用的 SDK 来与目前提供服务的的 Open AI 进行交互组件:https://github.com/devlive-commun…...

1.Introduction to Spring Web MVC framework
Web MVC framework 文档:22. Web MVC framework (spring.io) 概述 Web MVC框架(Web Model-View-Controller Framework)是一种用于构建Web应用程序的软件架构模式。MVC模式将应用程序分为三个主要组件:模型(Model&am…...

Onnx 1-深度学习-概述1
Onnx 1-深度学习-概述1 一: Onnx 概念1> Onnx 介绍2> Onnx 的作用3> Onnx 应用场景4> Onnx 文件格式1. Protobuf 特点2. onnx.proto3协议3> Onnx 模型基本操作二:Onnx API1> 算子详解2> Onnx 算子介绍三: Onnx 模型1> Onnx 函数功能1. np.random.rand…...

网络基础——udp协议
UDP协议(User Datagram Protocol,用户数据报协议)是OSI(Open System Interconnection,开放式系统互联)参考模型中一种无连接的传输层协议,它提供了一种简单的、不可靠的数据传输服务。以下是关于…...

分布式锁理解
介绍分布式锁,我觉得从项目的背景入手把 在伙伴匹配系统中,我创建了一个定时任务,做为缓存预热的手段 这个具体原因在Redis-CSDN博客 接下来切入正题: 想象每个服务器都有一个定时任务,都要对数据库或者缓存进行操…...
: Gradle 脚本最佳实践)
Android Gradle 开发与应用 (十): Gradle 脚本最佳实践
目录 1. 使用Gradle Kotlin DSL 1.1 什么是Gradle Kotlin DSL 1.2 迁移到Kotlin DSL 1.3 优势分析 2. 优化依赖管理 2.1 使用依赖版本管理文件 2.2 使用依赖分组 3. 合理使用Gradle插件 3.1 官方插件和自定义插件 3.2 插件管理的最佳实践 4. 任务配置优化 4.1 使用…...
)
c#获取本机的MAC地址(附源码)
在前一次的项目中,突然用到了这个获取本机的MAC地址,然后就研究了一下,记录下来,防止以后再用到, 使用winfrom做的,界面一个button,一个textBox,点了button以后给textBox赋值显示mac地址 附上源…...

sqlmap使用之-post注入、head注入(ua、cookie、referer)
1、post注入 1.1、方法一,通过保存数据包文件进行注入 bp抓包获取post数据 将数据保存到post.txt文件 加上-r指定数据文件 1.2、方法二、通过URL注入 D:\Python3.8.6\SQLmap>python sqlmap.py -u "http://localhost/login.php" --data "userna…...

XSS: 原理 反射型实例[入门]
原理 服务器未对用户输入进行严格校验,使攻击者将恶意的js代码,拼接到前端代码中,从而实现恶意利用 XSS攻击危害 窃取用户Cookie和其他敏感信息,进行会话劫持或身份冒充后台增删改文章进行XSS钓鱼攻击利用XSS漏洞进行网页代码的…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
