核密度估计KDE和概率密度函数PDF(深入浅出)
目录
- 1. 和密度估计(KDE)
- 核密度估计的基本原理
- 核密度估计的公式
- 核密度估计的应用
- Python中的KDE实现
- 示例代码
- 结果解释
- 解释结果
- 总结
- 2. 概率密度函数(PDF)
- 概率密度函数(PDF)是怎么工作的:
- 用图画来解释
- 解释这个图:
- 问题解答:
- 总结
- 3. 核密度估计(KDE)和概率密度函数(PDF)之间的关系
- 故事开始:
- 第一种方法:概率密度函数(PDF)
- 第二种方法:核密度估计(KDE)
- 总结一下:
- 问题解答:
1. 和密度估计(KDE)
KDE,全称为核密度估计(Kernel Density Estimation),是一种非参数方法,用于估计随机变量的概率密度函数。与传统的直方图不同,KDE能够提供一个更平滑和连续的密度估计,适用于更细致的分布分析。
核密度估计的基本原理
核密度估计通过对每个数据点应用一个核函数,并将这些核函数进行叠加来构建密度估计。核函数通常是一个对称的、非负的函数,具有单位面积。常见的核函数包括高斯核(Gaussian kernel)、均匀核(Uniform kernel)、三角核(Triangular kernel)等。
核密度估计的公式
给定样本数据 { x 1 , x 2 , … , x n } \{x_1, x_2, \ldots, x_n\} {x1,x2,…,xn},核密度估计的公式为:
f ^ ( x ) = 1 n h ∑ i = 1 n K ( x − x i h ) \hat{f}(x) = \frac{1}{n h} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right) f^(x)=nh1i=1∑nK(hx−xi)
其中:
- f ^ ( x ) \hat{f}(x) f^(x) 是在点 x x x 处的估计密度值。
- K K K 是核函数。
- h h h 是带宽(平滑参数),控制估计的平滑程度。带宽越大,估计越平滑;带宽越小,估计越细致。
核密度估计的应用
核密度估计在数据分析和统计建模中有广泛应用,特别是在探索性数据分析中,用于查看数据分布的形状和特性。
Python中的KDE实现
在Python中,SciPy和Seaborn库提供了便捷的核密度估计功能。以下是一个使用Seaborn和SciPy进行核密度估计的示例:
示例代码
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
import seaborn as sns# 生成一些示例数据
data = np.random.normal(0, 1, size=1000)# 使用SciPy进行核密度估计
kde_scipy = gaussian_kde(data, bw_method=0.3)
x = np.linspace(min(data), max(data), 1000)
kde_values = kde_scipy(x)# 使用Seaborn进行核密度估计和绘图
plt.figure(figsize=(10, 6))
sns.histplot(data, kde=True, stat="density", bins=30, label='Histogram with KDE', color='blue', alpha=0.6)
plt.plot(x, kde_values, color='red', lw=2, label='KDE (SciPy)')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.title('Kernel Density Estimation')
plt.show()
结果解释
在这个示例中:
- 生成了一些服从正态分布的示例数据。
- 使用SciPy的
gaussian_kde函数进行了核密度估计,并绘制了估计的密度曲线。 - 使用Seaborn的
histplot函数绘制了包含KDE的直方图。
解释结果
核密度估计图展示了数据的平滑分布,与传统的直方图相比,KDE图更为连续和平滑,能够更好地反映数据的实际分布情况。
总结
核密度估计(KDE)是一种强大的工具,用于估计和可视化数据的概率密度函数。它通过平滑的数据分布提供了比直方图更细致的分布视图,在数据分析中非常有用。
2. 概率密度函数(PDF)
概率密度函数(PDF) 是用来描述连续随机变量在某个特定值附近的可能性的一种函数。它帮助我们理解数据是如何分布的。
想象一下你在一个游乐园里玩捞鱼游戏。
- 你有一个大水池,里面有很多小鱼,每条鱼的位置都不一样。
- 如果你想知道在某个特定位置附近有多少鱼,你可以用一个网在那个位置捞鱼。
- 如果在这个位置附近有很多鱼,那这个位置的“鱼密度”就很高。
- 如果只有几条鱼,那这个位置的“鱼密度”就很低。
概率密度函数(PDF)是怎么工作的:
-
表示密度:
- PDF 就像是一个“鱼密度”图。它告诉你在水池的每个位置,鱼的密度有多高。
- PDF 的值可以很大,表示这个位置附近的鱼很多。PDF 的值也可以很小,表示这个位置附近的鱼很少。
-
总面积为1:
- 虽然 PDF 的值可以很高,但整个水池的密度总和必须是1。这表示所有的鱼都在这个水池里。
-
计算概率:
- 如果你想知道在一个范围内捞到鱼的概率,你可以看这个范围内的“鱼密度”图,然后把这个范围内的密度值加起来。
- 比如,如果你想知道在水池左边1/4的地方捞到鱼的概率,你可以看这部分的“鱼密度”图,然后加起来。这就是PDF的积分。
用图画来解释
假设我们有一个简单的例子,水池里鱼的密度是这样的:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm# 定义均值和标准差
mu = 0
sigma = 1# 生成数据点
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 1000)
pdf = norm.pdf(x, mu, sigma)# 绘制正态分布的概率密度函数
plt.plot(x, pdf, 'r-', lw=2, label='PDF')
plt.fill_between(x, pdf, alpha=0.5, color='red')
plt.xlabel('位置')
plt.ylabel('密度')
plt.title('鱼密度图(概率密度函数)')
plt.legend(loc='best')
plt.show()
解释这个图:
- 横轴表示水池的位置。
- 纵轴表示鱼的密度。
- 曲线上的每个点表示在那个位置附近的鱼的密度。
- 红色的区域表示鱼的密度,整个红色区域的面积总和是1。
问题解答:
问:为什么有些位置的密度会很高呢?
答:就像在水池里,如果很多鱼集中在某个地方,这个地方的密度就会很高。概率密度函数(PDF)也是一样,它告诉我们在数据中某些值附近数据有多集中。如果很多数据都集中在一个值附近,这个值的密度就会很高。
总结
- PDF 就像是一个密度图,它告诉我们数据在不同位置的密度有多高。
- 总面积为1 表示所有的数据都在这个范围内。
- PDF的值 可以很大,但它表示的是密度,而不是直接的数量。
希望这个解释能够帮助小朋友理解概率密度函数(PDF)的基本概念。如果有更多问题,随时可以问我哦!
3. 核密度估计(KDE)和概率密度函数(PDF)之间的关系
核密度估计(KDE)和概率密度函数(PDF)是用来表示数据分布的两种方法。我们可以通过一个简单的故事来帮助理解它们之间的关系。
故事开始:
想象一下,你在生日派对上有一个大蛋糕,你和你的朋友们都喜欢不同口味的蛋糕。为了让每个人都开心,你决定用两种方法来展示大家最喜欢的口味。
第一种方法:概率密度函数(PDF)
PDF就像是在蛋糕上插蜡烛
- 想象一个蛋糕,每个蛋糕上面插满了蜡烛。每个蜡烛代表一个不同口味的蛋糕片。
- 如果某种口味有很多蜡烛,就意味着很多人喜欢这个口味。比如,如果巧克力味的蛋糕上插了很多蜡烛,那说明大家都很喜欢巧克力味。
- 但是这些蜡烛的高度可以非常高,也可以非常低。即使有些蜡烛很高,也不代表这些口味的蛋糕片会比其他口味的蛋糕片更多。
第二种方法:核密度估计(KDE)
KDE就像是用蛋糕刀把蛋糕切成很多片
- 想象现在你拿了一把蛋糕刀,把整个蛋糕切成很多片,每片蛋糕代表不同口味的蛋糕。
- 当你切蛋糕的时候,每个切片的大小表示有多少人喜欢这个口味。如果某个口味有很多人喜欢,这个切片就会比较大。
- 切片之间的边界是平滑的,没有突然的变化。这使得每个切片的大小表示的更加平滑和准确。
总结一下:
- PDF:就像蛋糕上的蜡烛。蜡烛越高,表示那个地方的数据越密集,但是蜡烛高度可以超过1米,因为它表示的是密度。
- KDE:就像用蛋糕刀切蛋糕。切片的大小表示数据的密度,切得越平滑,表示数据分布越连续。
问题解答:
问:为什么蜡烛有时会很高呢?
答:蜡烛的高度表示密度。即使高度超过1米,它表示的是数据集中在那个位置的密度,而不是直接的数量。KDE的平滑切片能更好地展示每种口味在整个蛋糕中的分布情况。
相关文章:

核密度估计KDE和概率密度函数PDF(深入浅出)
目录 1. 和密度估计(KDE)核密度估计的基本原理核密度估计的公式核密度估计的应用Python中的KDE实现示例代码 结果解释解释结果 总结 2. 概率密度函数(PDF)概率密度函数(PDF)是怎么工作的:用图画…...

免开steam 脱离steam 进行游戏的小工具
链接:https://pan.baidu.com/s/1k2C8b4jEqKIGLtLZp8YCgA?pwd6666 提取码:6666 我们只需选择游戏根目录 然后输入AppID 点击底部按钮 进行就可以了 关于AppID在:...

深度学习--系统配置流程
Win10系统配置双系统Ubuntu18.04 深度学习台式服务器自装练手1.win10磁盘管理2.下载系统镜像制作U盘3.系统安装4. 安装后的系统设置工作5.配置CUDA环境CUDNN安装 深度学习台式服务器自装练手 写在最前 CUDA最高支持11.4 显卡3060 1.win10磁盘管理 首先对原有磁盘进行分区整理…...

把Docker的虚拟磁盘文件移动到别的盘符
今天清理C盘空间,发现一个很大的文件 ext4.vhdx 足有 15G 之多,发现这个是Docker的虚拟磁盘文件,于是在网上找到移到它的办法,使用 PowerShell 执行下面命令 查看Docker状态和版本 wsl -l -v 关闭Docker服务 wsl --shutdown …...

Oracle 19c RAC 心跳异常处理
客户机房异常断电后,启动19c集群报错如下 2024-07-05 17:43:27.934 [GIPCD(5964292)]CRS-42216: No interfaces are configured on the local node for interface definition en3(:.*)?:100.100.100.0: available interface definitions are [en0(:.*)?:10.88.0.…...

微信小程序引入自定义子组件报错,在 C:/Users/***/WeChatProjects/miniprogram-1/components/路径下***
使用原生小程序开发时候,会报下面的错误, [ pages/button/button.json 文件内容错误] pages/button/button.json: [“usingComponents”][“second-component”]: “…/…/components/second-child/index”,在 C:/Users/***/WeChatProjects/m…...
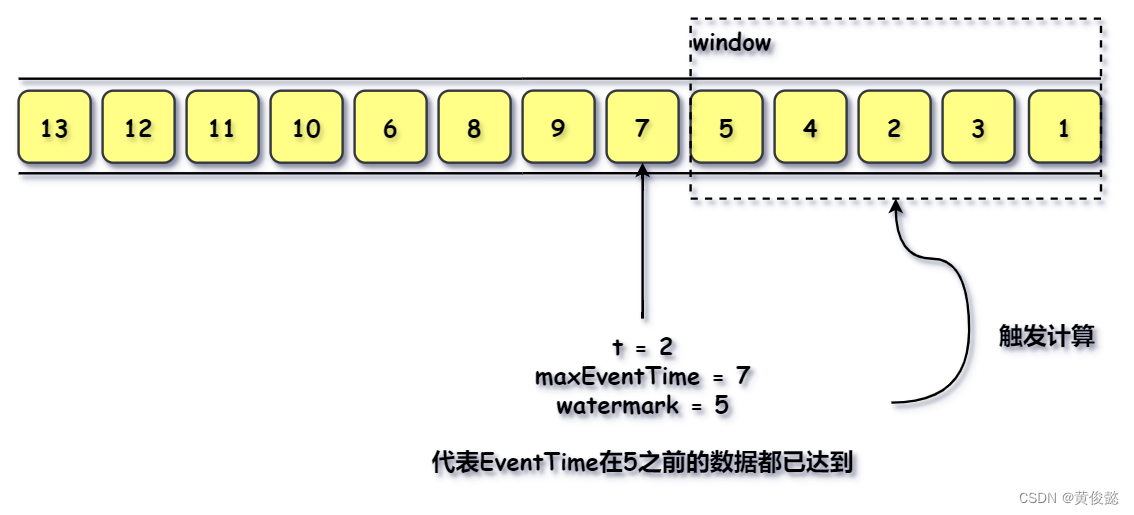
【图解大数据技术】流式计算:Spark Streaming、Flink
【图解大数据技术】流式计算:Spark Streaming、Flink 批处理 VS 流式计算Spark StreamingFlinkFlink简介Flink入门案例Streaming Dataflow Flink架构Flink任务调度与执行task slot 和 task EventTime、Windows、WatermarksEventTimeWindowsWatermarks 批处理 VS 流式…...

启动完 kubelet 日志显示 failed to get azure cloud in GetVolumeLimits, plugin.host: 1
查看 kubelet 日志组件命令 journalctl -xefu kubelet 文字描述问题 Jul 09 07:45:17 node01 kubelet[1344]: I0709 07:45:17.410786 1344 operation_generator.go:568] MountVolume.SetUp succeeded for volume "default-token-mfzqf" (UniqueName: "ku…...
C语言基础and数据结构
C语言程序和程序设计概述 程序:可以连续执行的一条条指令的集合 开发过程:C源程序(.c文件) --> 目标程序(.obj二进制文件,目标文件) --> 可执行文件(.exe文件) -->结果 在任何机器上可以运行C源程序生成的 .exe 文件 没有安装C语言集成开发环境,不能编译C语言程…...

【超万卡GPU集群关键技术深度分析 2024】_构建10万卡gpu集群的技术挑战
文末有福利! 1. 集群高能效计算技术 随着大模型从千亿参数的自然语言模型向万亿参数的多模态模型升级演进,超万卡集群吸需全面提升底层计算能力。 具体而言,包括增强单芯片能力、提升超节点计算能力、基于 DPU (Data Processing Unit) 实现…...

RuntimeError: CUDA error: invalid device ordinal
RuntimeError: CUDA error: invalid device ordinal 报错分析:可能原因1:设置CUDA_VISIBLE_DEVICES的问题解决办法: 可能原因2:硬件或驱动原因解决方法: 参考资料 报错分析: 如果你在运行代码时报错&#…...

如何在Qt中添加文本
在Qt中添加文本通常涉及到使用几种不同的Qt控件,具体取决于你想要在何处以及以何种方式显示文本。以下是一些常见的方法: 1. 使用QLabel显示文本 QLabel是Qt中用于显示文本或图片的简单控件。你可以通过构造函数或setText()方法设置其显示的文本。 #i…...

解决打印PDF文本不清楚的处理办法
之前打印PDF格式的电子书,不清晰,影响看书的心情,有时看到打印的书的质量,根本不想看,今天在打印一本页数不多,但PDF格式的书感觉也不太清楚,我想应该有办法解决,我使用的是解决福昕…...

【Cesium开发实战】火灾疏散功能的实现,可设置火源点、疏散路径、疏散人数
Cesium有很多很强大的功能,可以在地球上实现很多炫酷的3D效果。今天给大家分享一个可自定义的火灾疏散人群的功能。 1.话不多说,先展示 火灾疏散模拟 2.设计思路 根据项目需求要求,可设置火源点、绘制逃生路线、可设置逃生人数。所以点击火…...

imx6ull/linux应用编程学习(16)emqx ,mqtt创建连接mqtt.fx
在很多项目中都需要自己的私人服务器,以保证数据的隐私性,这里我用的是emqx。 1.进入emqx官网 EMQX:用于物联网、车联网和工业物联网的企业级 MQTT 平台 点击试用cloud 申请成功后可得:(右边的忽略) 进入…...

Debezium系列之:验证mysql、mariadb等兼容mysql协议数据库账号权限
Debezium系列之:验证mysql、mariadb等兼容mysql协议数据库账号权限 一、数据库需要开启binlog二、创建账号和账号需要赋予的权限三、账号具有权限查看日志信息四、验证账号权限五、验证账号能否执行show master status六、验证数据库是否开启binlog一、数据库需要开启binlog …...

Vue.js学习笔记(五)抽奖组件封装——转盘抽奖
基于VUE2转盘组件的开发 文章目录 基于VUE2转盘组件的开发前言一、开发步骤1.组件布局2.布局样式3.数据准备 二、最后效果总结 前言 因为之前的转盘功能是图片做的,每次活动更新都要重做UI和前端,为了解决这一问题进行动态配置转盘组件开发,…...

使用pip或conda离线下载安装包,使用pip或conda安装离线安装包
使用pip或conda离线下载安装包,使用pip或conda安装离线安装包 一、使用pip离线下载安装包1. 在有网络的机器上下载包和依赖2. 传输离线安装包 二、在目标机器上离线安装pip包三、使用conda离线下载安装包1. 在有网络的机器上下载conda包2. 传输conda包或环境包3. 在…...

产品访问分析
1、DWD产品访问明细 1.1、用户产品权限数据 --用户产品权限数据INSERT OVERWRITE TABLE temp_lms.dm_lms_platform_usergroup_app_tmpselect 仓储司南 as pro_name,CCSN as pro_code,c.user_name as user_name,d.account_name …...

【算法】代码随想录之链表(更新中)
文章目录 前言 一、移除链表元素(LeetCode--203) 前言 跟随代码随想录,学习链表相关的算法题目,记录学习过程中的tips。 一、移除链表元素(LeetCode--203) 【1】题目描述: 【2】解决思想&am…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
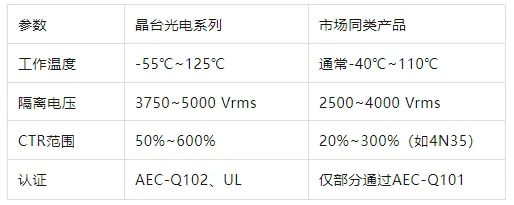
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
