java算法day13
java算法day13
- 104 二叉树的最大深度
- 111 二叉树的最小深度
- 226 翻转二叉树
- 101 对称二叉树
- 100 相同的树
104 二叉树的最大深度
我最开始想到的是用层序遍历。处理每一层然后计数。思路非常的清楚。
迭代法:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int maxDepth(TreeNode root) {Deque<TreeNode> que = new ArrayDeque<>();int deepth = 0;//特判if(root==null){return deepth;}//还是根节点先入栈。思想就是层序遍历。每处理完一层,那么就计数+1。que.offerLast(root);while(!que.isEmpty()){int size = que.size();while(size>0){TreeNode temp = que.pollFirst();if(temp.left!=null){que.offerLast(temp.left);}if(temp.right!=null){que.offerLast(temp.right);}size--;}deepth++;}return deepth;}
}
递归解法在下面
111 二叉树的最小深度
我一开始想到的还是层序遍历。
唯一的变化就是判断什么时候停下来,就是处理节点的时候,如果某个节点没有叶子节点,那不就说明这层之后该节点就没有孩子嘞。就是最小深度。
迭代解法:
class Solution {public int minDepth(TreeNode root) {Deque<TreeNode> que = new ArrayDeque<>();if(root==null){return 0;}int count = 1;que.offerLast(root);while(!que.isEmpty()){int size = que.size();while(size>0){TreeNode temp = que.pollFirst();if(temp.left==null && temp.right==null){return count;}if(temp.left!=null){que.offerLast(temp.left);}if(temp.right!=null){que.offerLast(temp.right);}size--;}count++;}return count;}
}
递归解法在下面
递归
接下来的题目几乎都用到了递归,这里就解决晕递归的问题。
写递归的时候要注意哪些?
1.不要一上来就扣细节,而是考虑这个过程中要做什么。
2.停止递归逻辑,处理逻辑,正常返回逻辑
这种在题解中称为子问题,和原问题模型。可以类比循环,在循环中我们总是要执行相同的逻辑,但是递归的特点在于,他需要在这个过程中,将计算的结果依次返给上一级。
想不到什么时候终止,就想想最底部的状态。
想不到处理逻辑怎么写,就想想如何进入下一层。
一句总结:想想怎么递下去,递到什么时候,什么时候归,归的过程中要干嘛。
二叉树的最大深度
思路:
正如递归的核心思想,不要上来就去扣递归的细节,而是想递归的过程中做了什么。
递归的过程我做了什么:最大的深度,就是左子树和右子树当中的最大深度,当返回上一层时,进行+1。
不从过程来考虑就是,return的结果就是左右子树的最大深度,然后到这一层嘞就是+1。感觉就是一眼看到了问题的本质。底部自己会去递归。
class Solution {public int maxDepth(TreeNode root) {if(root==null){return 0;}return Math.max(maxDepth(root.left),maxDepth(root.right))+1;}}
二叉树的最小深度
一上来先粗略的考虑,这个思路是正确的,粗略的考虑就是递归计算左右子树的最小深度,每一层返回上来的时候再+1。
这题如果按最大深度那样去想就做不出来了。因为一旦按那个套路去做,就没想到这种情况。
如果按之前那个套路,递归去算左右子树的最小高度,那在第一个节点,就会直接取到min,这显然不是想要的答案。那显然这个时候就要把这种情况给排除。
排除的方式就是做判断:
1.如果有一个节点为null了,那么你要判断能不能往下走。两个节点都为null了你才可以停。
2.两个节点都不为null,那就计算左右子树最小高度。

在递归的过程中,计算左右最小深度。然后进行上面所说的特判。
class Solution {public int minDepth(TreeNode root) {if(root==null){//递归出口,能到这说明后面没路走了return 0;}//计算左右子树最小深度int leftDepth = minDepth(root.left);int rightDepth = minDepth(root.right);//对上面说的特殊情况做判断,判断属于哪种if(root.left==null){return rightDepth+1;}if(root.right==null){return leftDepth+1;}//都不是上面说的两种情况,那就是二者去min。return Math.min(leftDepth,rightDepth)+1;}
}
226 翻转二叉树
上来还是宏观上考虑,就是节点的左右子树不停的做swap操作。如果节点空了就退出。
想到了就直接这么写。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {dfs(root);return root;}//每个节点都做reverse处理,然后下一层还是对左右子树做同样的处理。public void dfs(TreeNode root){if(root==null){return;}reverse(root);dfs(root.left);dfs(root.right);}//封装的一个函数。public void reverse(TreeNode root){TreeNode temp = root.left;root.left = root.right;root.right = temp;}
}
101 对称二叉树
这题看了这个图就知道递归过程中在干嘛了。
向下的过程可以发现,一直在比较左节点的左孩子是否和右节点的右孩子相等,右节点的左孩子是否和左节点的右孩子相等。所以每层向下一直在做这件事。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {//特判if(root==null){return true;}//开始递归return dfs(root.left,root.right);}boolean dfs(TreeNode left,TreeNode right){//递归出口if(left==null && right == null){return true;}//能走到这里,上一个判断没有出去,说明必有一为null。所以返回falseif(left==null || right == null){return false;}//走到这说明两个都不为null,那就判断值if(left.val != right.val){return false;}//往下一层走,就是判断左节点的左孩子,和右节点的右孩子。return dfs(left.left,right.right) && dfs(left.right,right.left);}
}
100 相同的树
这个更是简单。在递归的过程中,单纯在比较二者左右孩子是否相等。
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p==null && q == null){return true;}if(p==null || q==null){return false;}if(p.val != q.val){return false;}return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}
}
相关文章:

java算法day13
java算法day13 104 二叉树的最大深度111 二叉树的最小深度226 翻转二叉树101 对称二叉树100 相同的树 104 二叉树的最大深度 我最开始想到的是用层序遍历。处理每一层然后计数。思路非常的清楚。 迭代法: /*** Definition for a binary tree node.* public class…...

方便快捷传文件—搭建rsync文件传输服务器
比如我们有一个服务器,想把各个机器的文件都通过脚本传给这台机,用sftp或者直接rsync就必须输密码,肯定不行,做等效性免密又麻烦,怎么办呢,这么办! 在服务端 yum -y install rsync #编辑&…...

python调用qt编写的dll
报错:FileNotFoundError: Could not find module F:\pythonProject\MINGW\sgp4Lib.dll (or one of its dependencies). Try using the full path with constructor syntax. 只有两种情况: 1.路径不对 2.库的依赖不全 1、如果是使用了qt库的࿰…...
SCI一区级 | Matlab实现NGO-CNN-LSTM-Mutilhead-Attention多变量时间序列预测
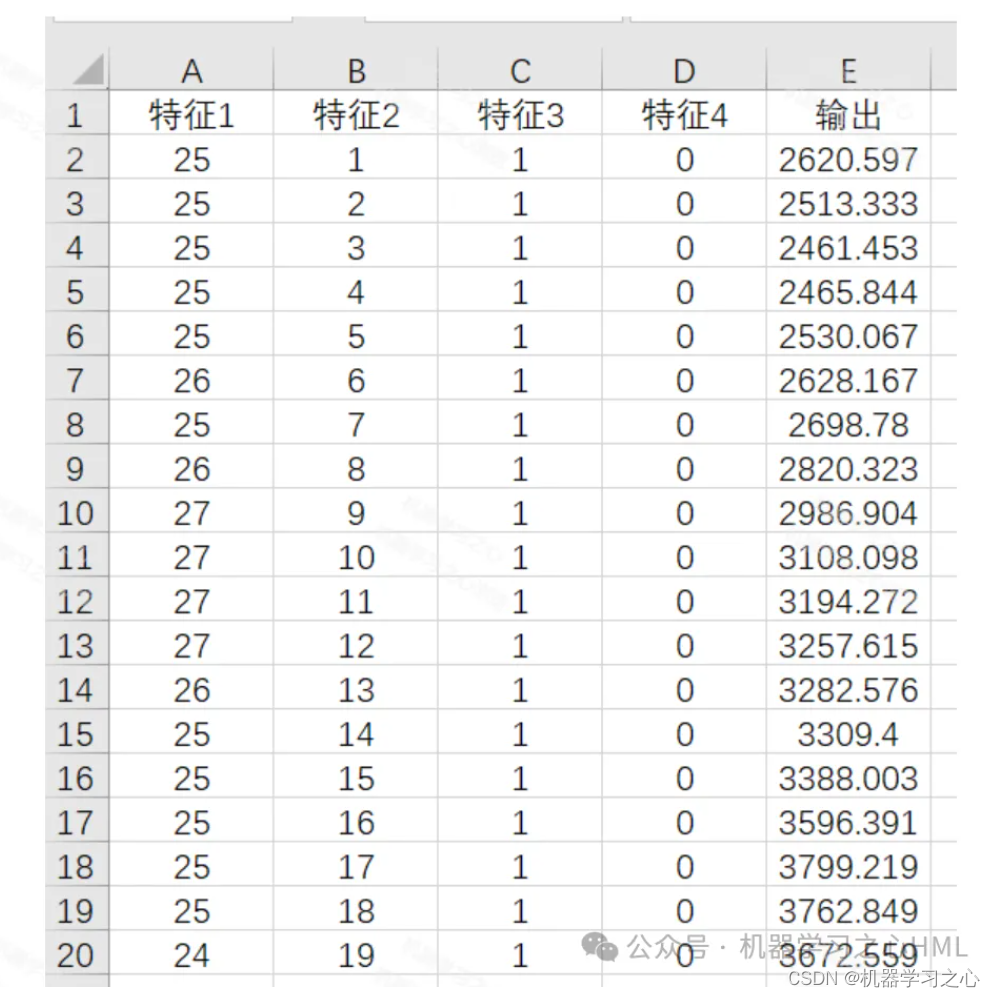
SCI一区级 | Matlab实现NGO-CNN-LSTM-Mutilhead-Attention多变量时间序列预测 目录 SCI一区级 | Matlab实现NGO-CNN-LSTM-Mutilhead-Attention多变量时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现NGO-CNN-LSTM-Mutilhead-Attention北方苍鹰算…...

【Redis】初识 Redis
文章目录 1 什么是 Redis2 Redis 的特点2.1 速度快2.2 可编程性2.3 可拓展性2.4 持久化2.5 主从复制2.5 高可用和分布式2.6 客户端语言多 3 Redis 使用场景3.1 实时数据存储3.2 缓存和 Session 存储3.3 消息队列 4 Redis 重大版本5 CentOS7 安装 Redis5 1 什么是 Redis Redis …...

【PTA天梯赛】L1-003 个位数统计(15分)
作者:指针不指南吗 专栏:算法刷题 🐾或许会很慢,但是不可以停下来🐾 文章目录 题目题解总结 题目 题目链接 题解 使用string把长度达1000位的数字存起来开一个代表个位数的数组 a[11]倒序计算最后一位,…...

c语言位操作符相关题目之交换两个数的值
文章目录 一、题目二、方法11,思路2,代码实现 三、方法21,思路2,代码实现 四、方法31,思路2,代码实现 总结 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目 实现两个变量的…...

智能家居装修怎么布线?智能家居网络与开关插座布置
打造全屋智能家居。计划的智能家居方案以米家系列为主,智能家居联网方案以无线为主。装修前为了装备智能家居做了很多准备工作,本文深圳侨杰智能分享一个智能家居装修和布线方面的心得与实战知识。希望能对大家的装修有所帮助。 1.关于网络 如果房子比…...

GD32MCU最小系统构成条件
大家是否有这个疑惑:大学课程学习51的时候,老师告诉我们51的最小系统构成?那么进入32位单片机时代,gd32最小系统构成又是怎么样的呢? 1.供电电路 需要确保供电的电压电流稳定,以东方红开发版为例ÿ…...

C语言——循环结构:while、do...while、for
while循环 基本结构 C语言中的while循环是一种基本的循环控制结构,它允许程序重复执行一段代码块,直到指定的条件不再满足为止。while循环的语法结构如下: while (condition) { // 循环体 // 在这里编写要重复执行的代码 } condition …...

C#实现最短路径算法
创建点集 double r 200 * 500;double width 1920;double height 1080;int col (int)(r / width);int row (int)(r / height);List<(double, double)> list1 new List<(double, double)>();for (int i 0; i < row; i){var y i * height;if (y < r){va…...

Python函数 之 匿名函数
1.概念 匿名函数: 使用 lambda 关键字 定义的表达式,称为匿名函数. 2.语法 lambda 参数, 参数: 一行代码 # 只能实现简单的功能,只能写一行代码 # 匿名函数 一般不直接调用,作为函数的参数使用的 3.代码 4.练习 # 1, 定义匿名函数, 参数…...

深入解析 Mybatis 中 Mapper 接口的实现原理
《深入解析 Mybatis 中 Mapper 接口的实现原理》 在使用 Mybatis 进行数据库操作时,Mapper 接口扮演着重要的角色。它提供了一种简洁、类型安全的方式来与数据库进行交互。那么,Mybatis 是如何实现 Mapper 接口的呢? 一、Mybatis 简介 Myb…...

微信小程序获取用户头像
微信为了安全更改了许多API接口,属实烦人。这次带来的是微信小程序基础库3.5.0还能使用的获取用户头像方法 按键式 <view><view><button open-type"chooseAvatar" bindchooseavatar"onGetUserImage">获取用户头像</butto…...

uniapp小程序连接蓝牙设备
uniapp小程序连接蓝牙设备 一、初始化蓝牙模块二、开始搜索三、连接蓝牙四、监听特征值变化五、调用示例utils.js文件 一、初始化蓝牙模块 这一步是必须的,在开发项目过程中,初始化蓝牙模块之后,紧接着就要开启一些监听的api,供后…...

AI大模型推理过程与优化技术深度剖析
在人工智能的浩瀚星空中,AI大模型以其卓越的性能和广泛的应用前景,成为了推动技术进步的璀璨明星。本文旨在深入探讨AI大模型的推理过程及其背后的优化技术,为理解这一复杂而精妙的技术体系提供一个清晰的视角。 一、AI大模型的推理过程揭秘 …...

Dubbo 核心概念介绍
Dubbo 是一款阿里巴巴开源的高性能 RPC(远程过程调用)框架,广泛应用于微服务架构中。它主要解决服务治理、负载均衡、故障转移等分布式系统问题。本文将介绍 Dubbo 的核心概念,包括服务提供者(Provider)、服…...

练习 6.7:⼈们 在为练习 6.1 编写的程序中,再创建两个表⽰⼈的字典,然后将这三个字典都存储在⼀个名为 people 的列表中。
练习 6.7:⼈们 在为练习 6.1 编写的程序中,再创建两个表⽰⼈的字典,然后将这三个字典都存储在⼀个名为 people 的列表中。 要求 遍历这个列表,将其中每个⼈的所有信息都打印出来。 代码 human {shuicc: {first_name: shui,la…...

星环科技知识平台TKH:引领企业构建高效AI基础设施,加速数智化转型新纪元
5月30-31日,2024向星力未来数据技术峰会期间,星环科技正式发布其最新人工智能基础设施产品——Transwarp Knowledge Hub星环知识平台(以下简称TKH)。该平台旨在为企业打通从人工智能基础设施建设到大数据、人工智能等研发应用的完…...
80道面试题及参考答案(3万字长文))
嵌入式板级支持包(BSP)80道面试题及参考答案(3万字长文)
目录 解释什么是通用输入输出(GPIO)接口及其在BSP中的作用。 描述SPI接口的主要特点和用途。 说明IC总线协议的工作原理。 如何在BSP中配置一个UART接口? USB设备控制器在BSP中的初始化步骤是什么? 以太网接口如何在BSP中被支持? 什么是SDIO,它在哪些场景下会被使…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
