C#实现最短路径算法
创建点集
double r = 200 * 500;double width = 1920;double height = 1080;int col = (int)(r / width);int row = (int)(r / height);List<(double, double)> list1 = new List<(double, double)>();for (int i = 0; i < row; ++i){var y = i * height;if (y < r){var xxx = Math.Sqrt(r * r - y * y);var x = xxx - (xxx % width);list1.Add((x, y));list1.Add((-x, y));list1.Add((x, -y));list1.Add((-x, -y));}}点阵像这样一样

最短路径算法,使用LinkedList返回,后续对插入友好
LinkedList<(double, double)> NearestNeighborTSP(List<(double, double)> points){int n = points.Count;bool[] visited = new bool[n];visited[0] = true;int current = 0;LinkedList<(double, double)> path = new LinkedList<(double, double)>();path.AddLast(points[current]);for (int i = 1; i < n; i++){double minDistance = double.MaxValue;int next = -1;for (int j = 0; j < n; j++){if (!visited[j]){double dist = Distance(points[current], points[j]);if (dist < minDistance){minDistance = dist;next = j;}}}current = next;visited[current] = true;path.AddLast(points[current]);}path.AddLast(points[0]);return path;}double Distance((double, double) point1, (double, double) point2){return Math.Sqrt(Math.Pow(point1.Item1 - point2.Item1, 2) + Math.Pow(point1.Item2 - point2.Item2, 2));}路径找完之后(局部展示图,斜线连起来的)

矫正斜线
var currentNode = res.First;while (currentNode != null && currentNode.Next != null){var nextNode = currentNode.Next;if (currentNode.Value.Item1 != nextNode.Value.Item1 && currentNode.Value.Item2 != nextNode.Value.Item2){var tempX = Math.Min(currentNode.Value.Item1, nextNode.Value.Item1);var tempY = currentNode.Value.Item1 > nextNode.Value.Item1 ? currentNode.Value.Item2 : nextNode.Value.Item2;res.AddAfter(currentNode, (tempX, tempY));currentNode = nextNode; // Skip the inserted node}elsecurrentNode = currentNode.Next;}矫正后效果

完整测试代码(demo中所用WPF框架,图表控件为ScottPlot5,nuget里直接搜,装5.0以上版本):
public void test(){double r = 200 * 500;double width = 1920;double height = 1080;int col = (int)(r / width);int row = (int)(r / height);List<(double, double)> list1 = new List<(double, double)>();for (int i = 0; i < row; ++i){var y = i * height;if (y < r){var xxx = Math.Sqrt(r * r - y * y);var x = xxx - (xxx % width);list1.Add((x, y));list1.Add((-x, y));list1.Add((x, -y));list1.Add((-x, -y));}}var wpfPlot = new ScottPlot.WPF.WpfPlot();var xs = list1.Select(x => x.Item1).ToArray();var ys = list1.Select(y => y.Item2).ToArray();var xx = wpfPlot.Plot.Add.Scatter(xs, ys, ScottPlot.Colors.Red).LineWidth = 0;var res = NearestNeighborTSP(list1);var currentNode = res.First;while (currentNode != null && currentNode.Next != null){var nextNode = currentNode.Next;if (currentNode.Value.Item1 != nextNode.Value.Item1 && currentNode.Value.Item2 != nextNode.Value.Item2){var tempX = Math.Min(currentNode.Value.Item1, nextNode.Value.Item1);var tempY = currentNode.Value.Item1 > nextNode.Value.Item1 ? currentNode.Value.Item2 : nextNode.Value.Item2;res.AddAfter(currentNode, (tempX, tempY));currentNode = nextNode; // Skip the inserted node}elsecurrentNode = currentNode.Next;}var xs2 = res.Select(x => x.Item1).ToArray();var ys2 = res.Select(x => x.Item2).ToArray();var yy = wpfPlot.Plot.Add.Scatter(xs2, ys2, ScottPlot.Colors.Blue).LineWidth = 1;grid.Children.Add(wpfPlot);}LinkedList<(double, double)> NearestNeighborTSP(List<(double, double)> points){int n = points.Count;bool[] visited = new bool[n];visited[0] = true;int current = 0;LinkedList<(double, double)> path = new LinkedList<(double, double)>();path.AddLast(points[current]);for (int i = 1; i < n; i++){double minDistance = double.MaxValue;int next = -1;for (int j = 0; j < n; j++){if (!visited[j]){double dist = Distance(points[current], points[j]);if (dist < minDistance){minDistance = dist;next = j;}}}current = next;visited[current] = true;path.AddLast(points[current]);}path.AddLast(points[0]);return path;}double Distance((double, double) point1, (double, double) point2){return Math.Sqrt(Math.Pow(point1.Item1 - point2.Item1, 2) + Math.Pow(point1.Item2 - point2.Item2, 2));}
}
相关文章:

C#实现最短路径算法
创建点集 double r 200 * 500;double width 1920;double height 1080;int col (int)(r / width);int row (int)(r / height);List<(double, double)> list1 new List<(double, double)>();for (int i 0; i < row; i){var y i * height;if (y < r){va…...

Python函数 之 匿名函数
1.概念 匿名函数: 使用 lambda 关键字 定义的表达式,称为匿名函数. 2.语法 lambda 参数, 参数: 一行代码 # 只能实现简单的功能,只能写一行代码 # 匿名函数 一般不直接调用,作为函数的参数使用的 3.代码 4.练习 # 1, 定义匿名函数, 参数…...

深入解析 Mybatis 中 Mapper 接口的实现原理
《深入解析 Mybatis 中 Mapper 接口的实现原理》 在使用 Mybatis 进行数据库操作时,Mapper 接口扮演着重要的角色。它提供了一种简洁、类型安全的方式来与数据库进行交互。那么,Mybatis 是如何实现 Mapper 接口的呢? 一、Mybatis 简介 Myb…...

微信小程序获取用户头像
微信为了安全更改了许多API接口,属实烦人。这次带来的是微信小程序基础库3.5.0还能使用的获取用户头像方法 按键式 <view><view><button open-type"chooseAvatar" bindchooseavatar"onGetUserImage">获取用户头像</butto…...

uniapp小程序连接蓝牙设备
uniapp小程序连接蓝牙设备 一、初始化蓝牙模块二、开始搜索三、连接蓝牙四、监听特征值变化五、调用示例utils.js文件 一、初始化蓝牙模块 这一步是必须的,在开发项目过程中,初始化蓝牙模块之后,紧接着就要开启一些监听的api,供后…...

AI大模型推理过程与优化技术深度剖析
在人工智能的浩瀚星空中,AI大模型以其卓越的性能和广泛的应用前景,成为了推动技术进步的璀璨明星。本文旨在深入探讨AI大模型的推理过程及其背后的优化技术,为理解这一复杂而精妙的技术体系提供一个清晰的视角。 一、AI大模型的推理过程揭秘 …...

Dubbo 核心概念介绍
Dubbo 是一款阿里巴巴开源的高性能 RPC(远程过程调用)框架,广泛应用于微服务架构中。它主要解决服务治理、负载均衡、故障转移等分布式系统问题。本文将介绍 Dubbo 的核心概念,包括服务提供者(Provider)、服…...

练习 6.7:⼈们 在为练习 6.1 编写的程序中,再创建两个表⽰⼈的字典,然后将这三个字典都存储在⼀个名为 people 的列表中。
练习 6.7:⼈们 在为练习 6.1 编写的程序中,再创建两个表⽰⼈的字典,然后将这三个字典都存储在⼀个名为 people 的列表中。 要求 遍历这个列表,将其中每个⼈的所有信息都打印出来。 代码 human {shuicc: {first_name: shui,la…...

星环科技知识平台TKH:引领企业构建高效AI基础设施,加速数智化转型新纪元
5月30-31日,2024向星力未来数据技术峰会期间,星环科技正式发布其最新人工智能基础设施产品——Transwarp Knowledge Hub星环知识平台(以下简称TKH)。该平台旨在为企业打通从人工智能基础设施建设到大数据、人工智能等研发应用的完…...
80道面试题及参考答案(3万字长文))
嵌入式板级支持包(BSP)80道面试题及参考答案(3万字长文)
目录 解释什么是通用输入输出(GPIO)接口及其在BSP中的作用。 描述SPI接口的主要特点和用途。 说明IC总线协议的工作原理。 如何在BSP中配置一个UART接口? USB设备控制器在BSP中的初始化步骤是什么? 以太网接口如何在BSP中被支持? 什么是SDIO,它在哪些场景下会被使…...

如何找回误删的文件?4个常用文件恢复方法!
对于许多用户来说,误删文件是一种常见而令人懊恼的情况。恢复误删文件的重要性在于,它可以帮助用户找回宝贵的数据,避免因数据丢失带来的各种不便和损失。 如何找回不小心删除的文件? 误删数据不知道怎么恢复,会给我…...

在大型企业级应用中,如何优化 XML 数据的存储和检索效率,以满足高并发访问需求?
在大型企业级应用中,优化XML数据的存储和检索效率可采取以下措施: 数据库选择:选择适合XML存储和查询的数据库,如Oracle、MySQL、PostgreSQL等。这些数据库提供了专门的XML存储和查询功能,能够更高效地处理XML数据。 …...

win10 A4000 下使用Xinference来进行大模型的推理测试
创建环境 conda remove --name xinference --all conda create --name xinference python3.10 conda activate xinference 安装: conda install pytorch torchvision torchaudio pytorch-cuda11.8 -c pytorch -c nvidia pip install tiktoken sentence-transformer…...

【9-2:代码规范】
算法级思想 代码规范(java) 代码规范(java) 方法参数必须一致,不要出现自动装箱拆箱操作SimpleDateFormat是线程不安全的使用equals注意空指针异常日志 事务场景中如果出现异常被捕时注意回滚不要再finally中使用retu…...
.generic_string()的bug)
std::filesystem::current_path().generic_string()的bug
这行指令出来会出来大小写的盘符,如D 或者d,似乎随机 #include <iostream> #include <filesystem>namespace fs std::filesystem;bool arePathsSame(const fs::path& p1, const fs::path& p2) {return p1 p2; }int main() {fs::p…...
Python excel知识库批量模糊匹配的3种方法实例(fuzzywuzzy\Gensim)
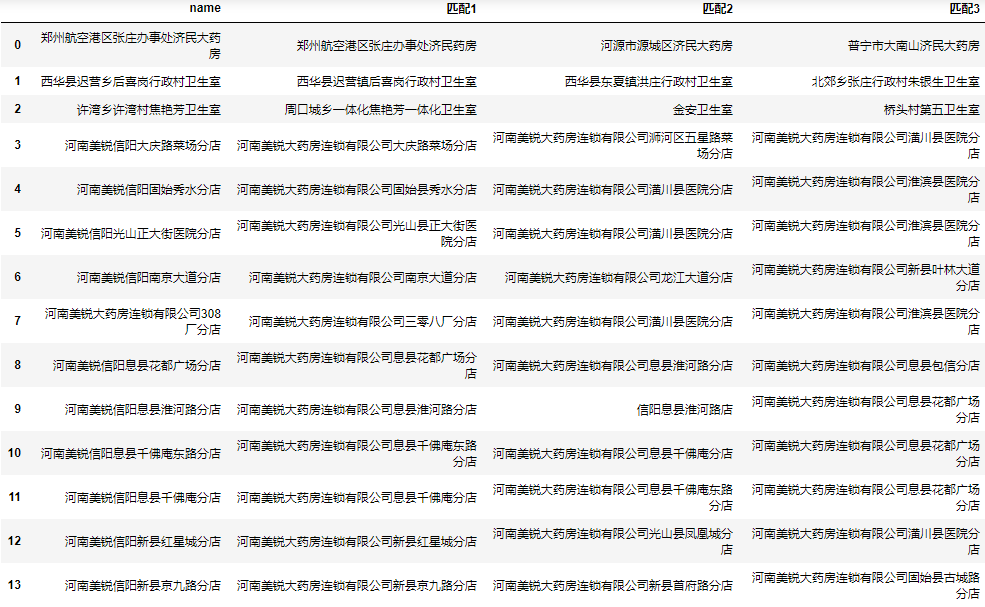
前言 当然,基于排序的模糊匹配(类似于Excel的VLOOKUP函数的模糊匹配模式)也属于模糊匹配的范畴,但那种过于简单,不是本文讨论的范畴。 本文主要讨论的是以公司名称或地址为主的字符串的模糊匹配。 使用编辑距离算法进…...

stm32使用单通道规则组ADC
Driver_ADC.c 如果需要关闭adc转换,只需要设置CNT,将其置为0,后面再转换一次就停止了。 #include "Driver_ADC.h"void Driver_ADC1_Init(void) {/* 1. 时钟配置 *//* 1.1 adc时钟 */RCC->APB2ENR | RCC_APB2ENR_ADC1EN;RCC-&g…...

[python][whl]causal-conv1d的python模块在windows上whl文件下载
【模块介绍】 causal-conv1d,即因果一维卷积(Causal 1D Convolution),是一种在深度学习特别是时序数据处理中广泛应用的卷积技术。它主要特点在于其“因果性”,即输出的每个元素仅依赖于输入序列中它之前的元素&#…...

介绍 CM3leon,一个更高效、最先进的文本和图像生成模型
近几个月来,随着让机器理解和表达语言的自然语言处理技术以及可根据文本输入生成图像的系统的进步,人们对生成式人工智能模型的兴趣和研究也在加速。今天,我们要展示的是 CM3leon(发音类似于 “变色龙”),它…...

HTTPS和HTTP有哪些区别
两者的主要区别在于安全性和数据加密: 加密层:HTTPS 在HTTP 的基础上增加了SSL/TLS 协议作为加密层,确保数据传输的安全性,即使数据被截获,没有相应的密钥也无法解读数据内容。而HTTP 数据传输是明文的,容易受到攻击。…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

aurora与pcie的数据高速传输
设备:zynq7100; 开发环境:window; vivado版本:2021.1; 引言 之前在前面两章已经介绍了aurora读写DDR,xdma读写ddr实验。这次我们做一个大工程,pc通过pcie传输给fpga,fpga再通过aur…...

SpringSecurity+vue通用权限系统
SpringSecurityvue通用权限系统 采用主流的技术栈实现,Mysql数据库,SpringBoot2Mybatis Plus后端,redis缓存,安全框架 SpringSecurity ,Vue3.2Element Plus实现后台管理。基于JWT技术实现前后端分离。项目开发同时采 …...

Unity基础-Mathf相关
Unity基础-Mathf相关 一、Mathf数学工具 概述 Mathf是Unity中封装好用于数学计算的工具结构体,提供了丰富的数学计算方法,特别适用于游戏开发场景。它是Unity开发中最常用的数学工具之一,能够帮助我们处理各种数学计算和插值运算。 Mathf…...

SQL 注入开放与修复
开发: SQL 注入是一种数据库攻击手段。攻击者通过向应用程序提交恶意代码来改变原 SQL 语句的含义, 进而执行任意 SQL 命令,达到入侵数据库乃至操作系统的目的。 例如:下面代码片段中,动态构造并执行了一个 SQ…...

FMC STM32H7 SDRAM
如何无痛使用片外SDRAM? stm32 已经成功初始化了 STM32H7 上的外部 SDRAM(32MB) 如何在开发中无痛使用SDRAM 使它像普通 RAM 一样“自然地”使用? [todo] 重要 MMT(Memory Management Tool) of STM32CubeMx The Memory Management Tool (MMT) disp…...
