Golang每日一练(leetDay0005)

目录
13. 罗马数字转整数 Roman to Integer ★
14. 最长公共前缀 Longest Common Prefix ★
15. 三数之和 3Sum ★★★
🌟 每日一练刷题专栏 🌟
Golang每日一练 专栏
Python每日一练 专栏
C/C++每日一练 专栏
Java每日一练 专栏
13. 罗马数字转整数 Roman to Integer
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。
示例 1:
输入: s = "III" 输出: 3
示例 2:
输入: s = "IV" 输出: 4
示例 3:
输入: s = "IX" 输出: 9
示例 4:
输入: s = "LVIII" 输出: 58 解释: L = 50, V= 5, III = 3.
示例 5:
输入: s = "MCMXCIV" 输出: 1994 解释: M = 1000, CM = 900, XC = 90, IV = 4.
提示:
1 <= s.length <= 15s仅含字符('I', 'V', 'X', 'L', 'C', 'D', 'M')- 题目数据保证
s是一个有效的罗马数字,且表示整数在范围[1, 3999]内 - 题目所给测试用例皆符合罗马数字书写规则,不会出现跨位等情况。
- IL 和 IM 这样的例子并不符合题目要求,49 应该写作 XLIX,999 应该写作 CMXCIX 。
- 关于罗马数字的详尽书写规则,可以参考 罗马数字(链接略) 。
代码:
package mainimport ("fmt"
)var roman = map[string]int{"I": 1,"V": 5,"X": 10,"L": 50,"C": 100,"D": 500,"M": 1000}func romanToInt(s string) int {if s == "" {return 0}num, lastint, total := 0, 0, 0for i := 0; i < len(s); i++ {char := s[len(s)-(i+1) : len(s)-i]num = roman[char]if num < lastint {total = total - num} else {total = total + num}lastint = num}return total
}func main() {fmt.Println(romanToInt("IX"))fmt.Println(romanToInt("LVIII"))fmt.Println(romanToInt("MCMXCIV"))}
输出:
9
58
1994
14. 最长公共前缀 Longest Common Prefix
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"] 输出:"fl"
示例 2:
输入:strs = ["dog","racecar","car"] 输出:"" 解释:输入不存在公共前缀。
提示:
1 <= strs.length <= 2000 <= strs[i].length <= 200strs[i]仅由小写英文字母组成
代码:
package mainimport ("fmt""strings"
)func longestCommonPrefix(strs []string) string {if len(strs) == 0 {return ""}prefix := strs[0]for i := 1; i < len(strs); i++ {for !strings.HasPrefix(strs[i], prefix) {prefix = prefix[:len(prefix)-1]if prefix == "" {return ""}}}return prefix
}func main() {fmt.Println(longestCommonPrefix([]string{"flower", "flow", "flight"}))fmt.Println(longestCommonPrefix([]string{"dog", "racecar", "car"}))}输出:
fl
说明:
将第一个字符串作为公共前缀的初始值,从第二个字符串开始依次与公共前缀进行比较。
如果当前字符串不是以公共前缀开头,则将公共前缀缩短一个字符,继续比较。
如果公共前缀已经为空,则说明不存在公共前缀,返回空字符串。
15. 三数之和 3Sum
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c,使得 a + b + c = 0?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = [] 输出:[]
示例 3:
输入:nums = [0] 输出:[]
提示:
0 <= nums.length <= 3000-10^5 <= nums[i] <= 10^5
代码1:
package mainimport ("fmt""sort"
)func threeSum(nums []int) [][]int {sort.Ints(nums) // 先将数组排序res := [][]int{}for i := 0; i < len(nums)-2; i++ {if i > 0 && nums[i] == nums[i-1] { // 跳过重复的元素continue}l, r := i+1, len(nums)-1 // 双指针for l < r {sum := nums[i] + nums[l] + nums[r]if sum == 0 {res = append(res, []int{nums[i], nums[l], nums[r]})for l < r && nums[l] == nums[l+1] { // 跳过重复的元素l++}for l < r && nums[r] == nums[r-1] { // 跳过重复的元素r--}l++r--} else if sum < 0 {l++} else {r--}}}return res
}func main() {fmt.Println(threeSum([]int{-1, 0, 1, 2, -1, -4}))fmt.Println(threeSum([]int{}))fmt.Println(threeSum([]int{0}))}
代码2:
package mainimport ("fmt""sort"
)func threeSum(nums []int) [][]int {sort.Ints(nums) // 先将数组排序n := len(nums)res := [][]int{}for i := 0; i < n; i++ {if i > 0 && nums[i] == nums[i-1] { // 去重continue}k := n - 1target := -nums[i]for j := i + 1; j < n; j++ {if j > i+1 && nums[j] == nums[j-1] { // 去重continue}for j < k && nums[j]+nums[k] > target { // 双指针k--}if j == k {break}if nums[j]+nums[k] == target {res = append(res, []int{nums[i], nums[j], nums[k]})}}}return res
}func main() {nums := []int{-1, 0, 1, 2, -1, -4}fmt.Println(threeSum(nums))fmt.Println(threeSum([]int{}))fmt.Println(threeSum([]int{0}))}
输出:
[[-1 -1 2] [-1 0 1]]
[]
[]
🌟 每日一练刷题专栏 🌟
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
 | Golang每日一练 专栏 |
 | Python每日一练 专栏 |
 | C/C++每日一练 专栏 |
 | Java每日一练 专栏 |
相关文章:

Golang每日一练(leetDay0005)
目录 13. 罗马数字转整数 Roman to Integer ★ 14. 最长公共前缀 Longest Common Prefix ★ 15. 三数之和 3Sum ★★★ 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 13. 罗马数字转…...
occt_modeling_data(一)——拓扑
下面是我基于opencascade英文文档中关于occt_modeling_data中Topology部分进行的翻译,英文好的还是建议直接看文档,部分我不肯定的地方我会附上英文原句。如发现有错误欢迎评论区留言。 OCCT Topolog允许用户访问和操纵物体的数据,且不需要处…...
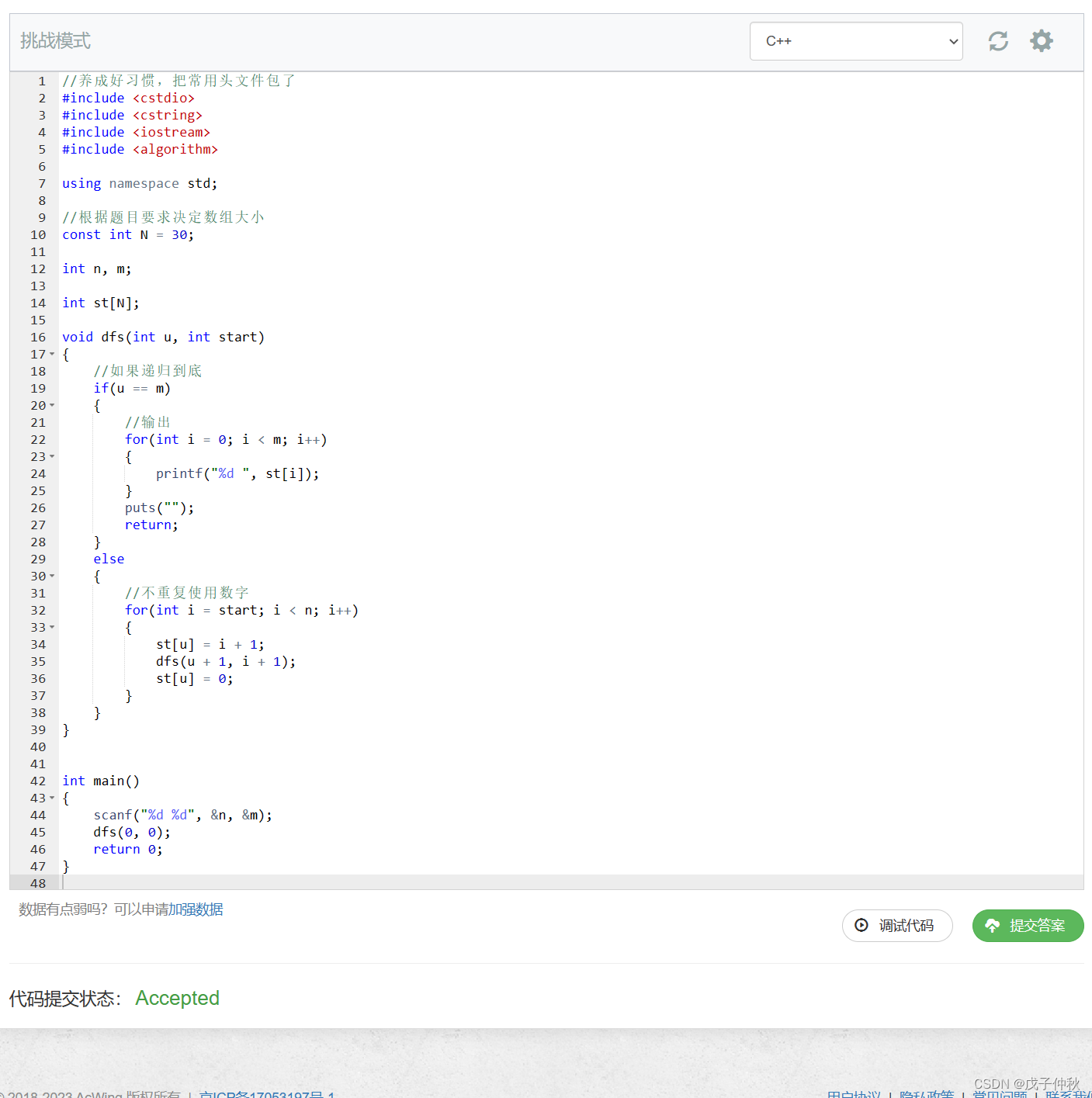
【AcWing】蓝桥杯备赛-深度优先搜索-dfs(3)
目录 写在前面: 题目:93. 递归实现组合型枚举 - AcWing题库 读题: 输入格式: 输出格式: 数据范围: 输入样例: 输出样例: 解题思路: 代码: AC &…...

宇宙最强-GPT-4 横空出世:最先进、更安全、更有用
文章目录前言一、准确性提升1.创造力2.视觉输入3.更长的上下文二、相比于ChatGPT有哪些提升1.GPT-4 的高级推理能力超越了 ChatGPT2.GPT-4 在多种测试考试中均优于 ChatGPT。三、研究团队在GPT-4模型都做了哪些改善1.遵循 GPT、GPT-2 和 GPT-3 的研究路径2.我们花了 6 个月的时…...
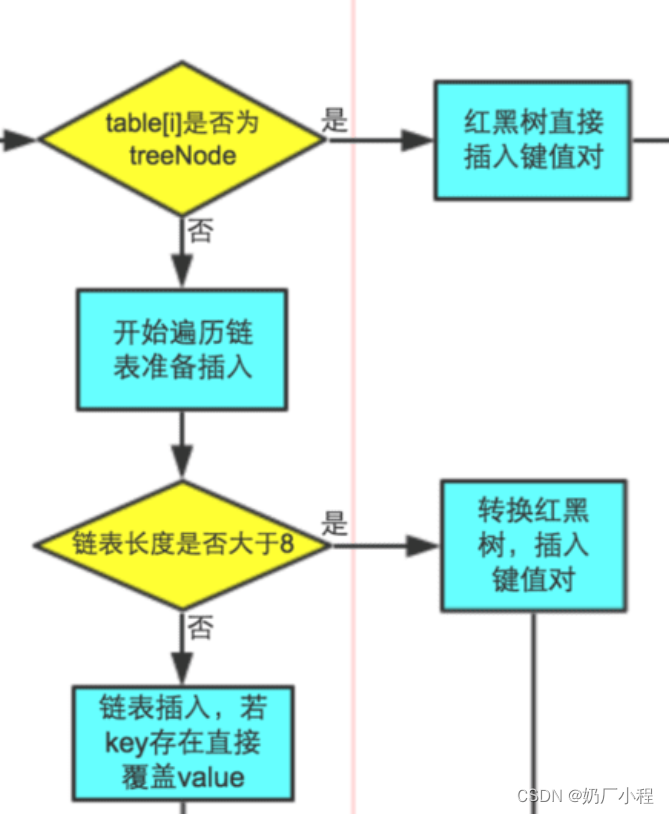
HashMap的实际开发使用
目 录 前言 一、HashMap是什么? 二、使用步骤 1.解析一下它实现的原理 编辑 2.实际开发使用 总结 前言 本章,只是大概记录一下hashMap的简单使用方法,以及理清一下hashMap的put方法的原理,以及get方法的原理。 一、Has…...

OpenCV入门(十三)快速学会OpenCV 12 图像梯度
OpenCV入门(十三)快速学会OpenCV 12 图像梯度1.Sobel算子1.1 计算x1.2 计算y1.3 计算xy2.Scharr算子2.1 计算x2.2 计算y2.3 计算xy3.Laplacian算子4.总结图像梯度计算的是图像变化的速度。对于图像的边缘部分,其灰度值变化较大,梯…...

软考:常见小题目计算题
01采购合同的类型采购合同主要包括总价类合同、成本补偿类合同、工料合同三大类合同。1、总价类合同此类合同为既定产品、服务或成果的采购设定一个总价。这种合同应在已明确定义需求,且不会出现重大范围变更的情况下使用。包括:(1࿰…...
【Linux】进程的程序替换
文章目录1. 程序替换1.创建子进程的目的是什么?2.了解程序是如何进行替换的3. 程序替换的基本原理当创建进程的时候,先有进程数据结构,还是先加载代码和数据?程序替换是整体替换,不是局部替换execl 返回值4. 替换函数1…...
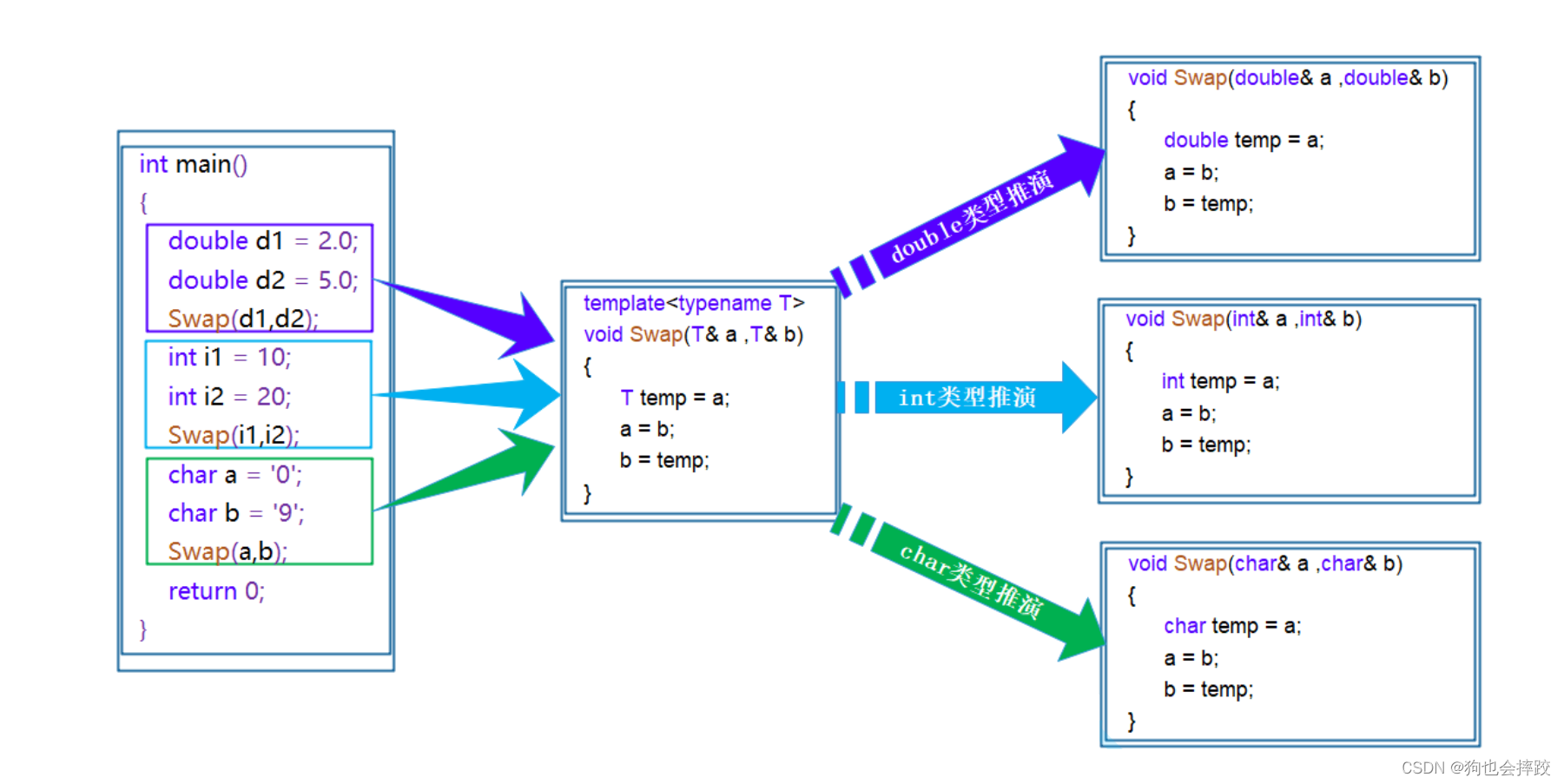
【C++】模板(上)
文章目录1、泛型编程2、函数模板函数模板的实例化模板参数的匹配原则3、 类模板类模板的实例化1、泛型编程 void Swap(int& left, int& right) {int temp left;left right;right temp; } void Swap(double& left, double& right) {double temp left;left …...
express框架利用formidable上传图片
express框架,在上传图片功能方面,用formidable里面的incomingform功能,很方便。很多功能都已经封装好了,非常好用,简单,不需要写更深层次的代码了。确实不错。 下面是我自己跟着黑马教程的博客系统的部分&…...
测试背锅侠?入职软件测试后大d佬给我丢了这个bug分类分析,至今受益匪浅......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 刚成为入职…...
STM32 OTA应用开发——通过内置DFU实现USB升级(方式1)
STM32 OTA应用开发——通过内置DFU实现USB升级(方式1) 目录STM32 OTA应用开发——通过内置DFU实现USB升级(方式1)前言1 硬件介绍2 环境搭建2.1 Keil uVsion2.2 zadig2.3 STM32CubeProgrammer2.4 安装USB驱动3 OTA升级结束语前言 …...
基于MFC的JavaScript进行网页数据交互
目录 前言 一、创建html对话框工程 二、使用步骤 1.引入JavaScript接口代码 2.重写相关接口 3.在html网页中添加C/C调用的接口 4.在MFC工程中添加调用接口 5.设置确认按键触发调用 6.运行结果 总结 前言 如何快速的进行MFC开发,这里我介绍一种JavaScript与C/C交互的…...
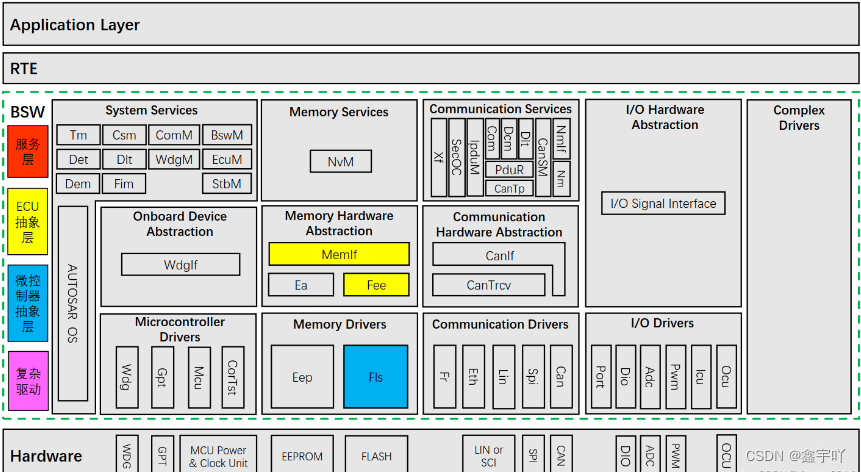
AUTOSAR-Fee
Fee模块 全称Flash EEPROM Emulation Module,属于ECU抽象层 Fee模块本身是脱离硬件的,但是Fee模块可能会引用的Fls模块定制API,所以只能算半抽象. FEE模块应从设备特定的寻址方案和分段中抽象出来,并为上层提供虚拟寻址方案和分段(virtual addressing scheme and segment…...
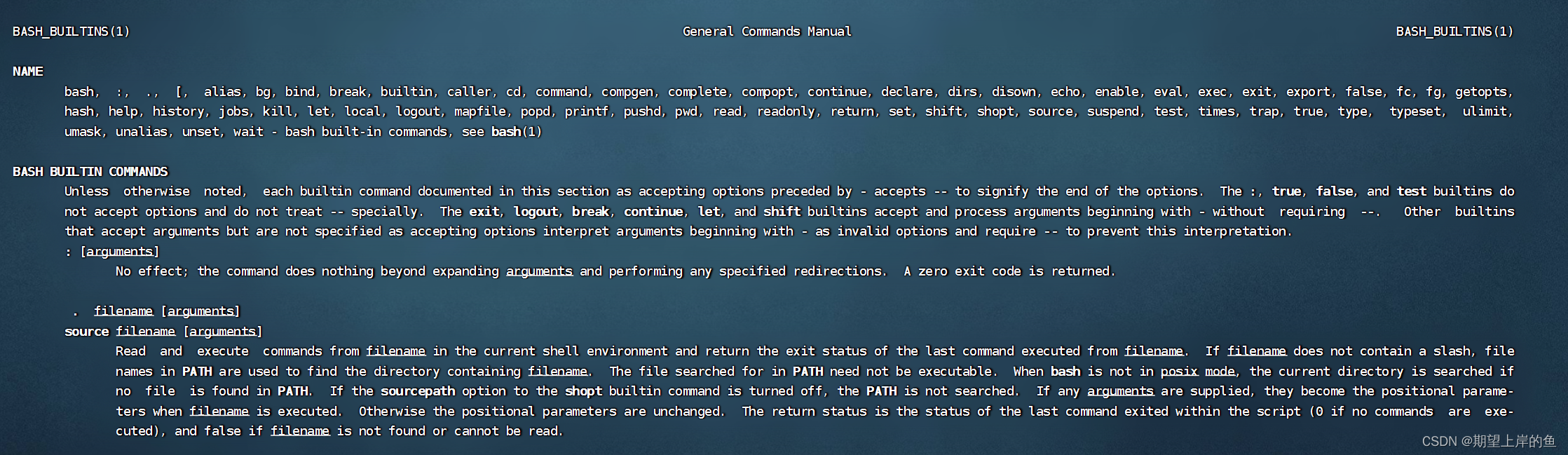
Linux基本命令——操作演示
Linux基本命令——操作演示Linux的目录结构Linux命令入门目录切换相关命令(cd/pwd)相对路径、绝对路径和特殊路径符创建目录命令(mkdir)文件操作命令part1 (touch、cat、more)文件操作命令part2 (cp、mv、rm)查找命令 …...
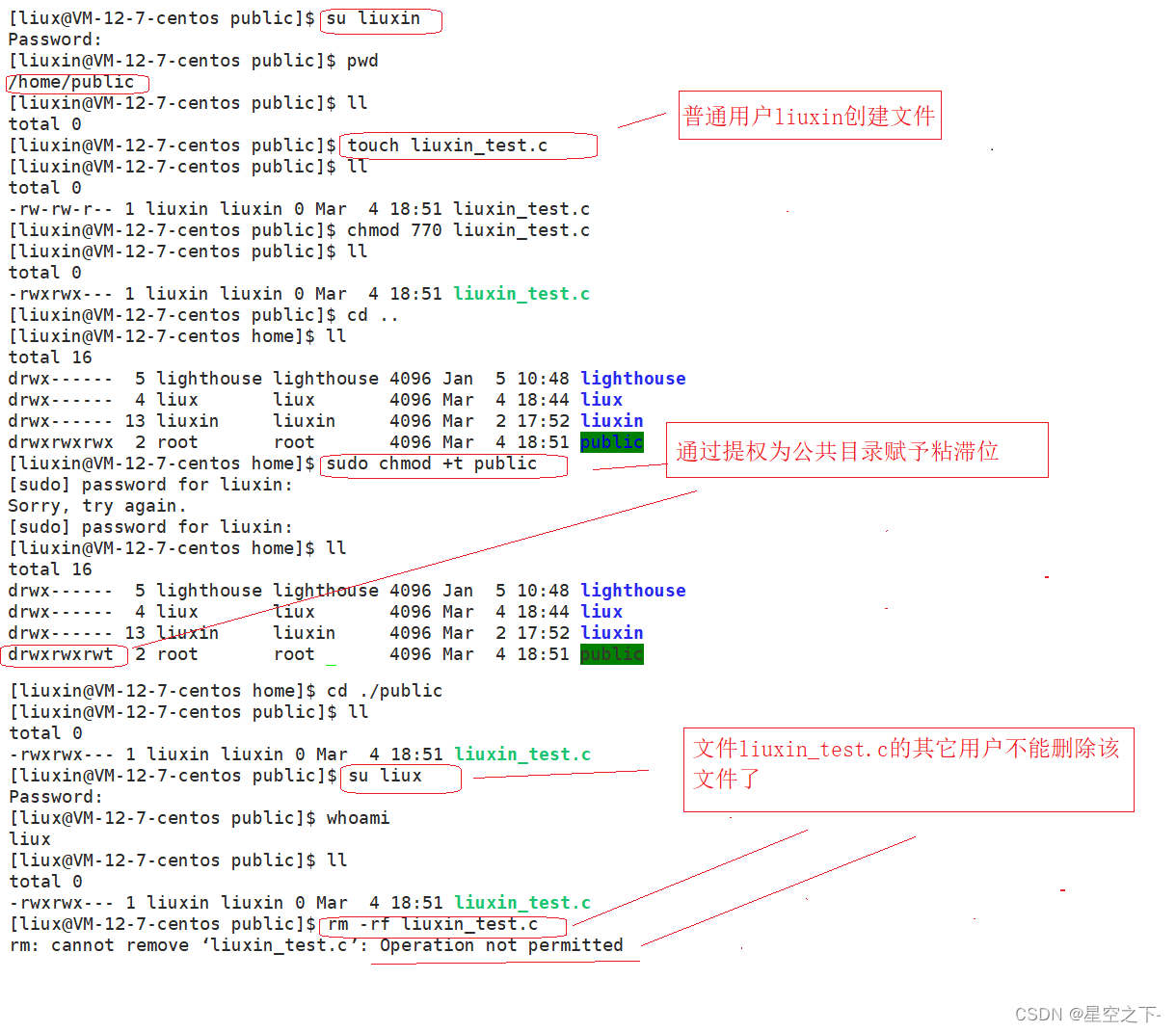
【Linux】目录和文件的权限
Linux中的权限有什么作用Linux权限管理文件访问者的分类文件类型和访问权限(事物属性)**文件权限值的表示方法**文件访问权限的相关设置方法chmodchownchgrpumaskumask使用 sudo分配权限目录的权限Linux中的权限有什么作用 Linux下有两种用户࿱…...

Unity 优化之Player Setting
Quality SettingPixel Light Count 使用前向渲染时最大像素光源数。也是性能关键。数量越大消耗越多。Texture Quality:贴图质量,可以选择Half Res,这样速度会更快,但是贴图质量会轻微下降。Anisotropic Textures 纹理各向异形Ant…...
)
Qt——通过一个简单的程序例程熟悉使用Qt Creator软件进行项目搭建的基本流程(新建项目、项目的文件组成、修改ui文件、编译运行与调试)
【系列专栏】:博主结合工作实践输出的,解决实际问题的专栏,朋友们看过来! 《项目案例分享》 《极客DIY开源分享》 《嵌入式通用开发实战》 《C++语言开发基础总结》 《从0到1学习嵌入式Linux开发》 《QT开发实战》 《Android开发实战》...
Linux 如何使用 git | 新建仓库 | git 三板斧
文章目录 专栏导读 一、如何安装 git 二、注册码云账号 三、新建仓库 配置仓库信息 四、克隆远端仓库到本地 五、git 三板斧 1. 三板斧第一招:git add 2. 三板斧第二招:git commit 解决首次 git commit 失败的问题 配置机器信息 3. 三…...
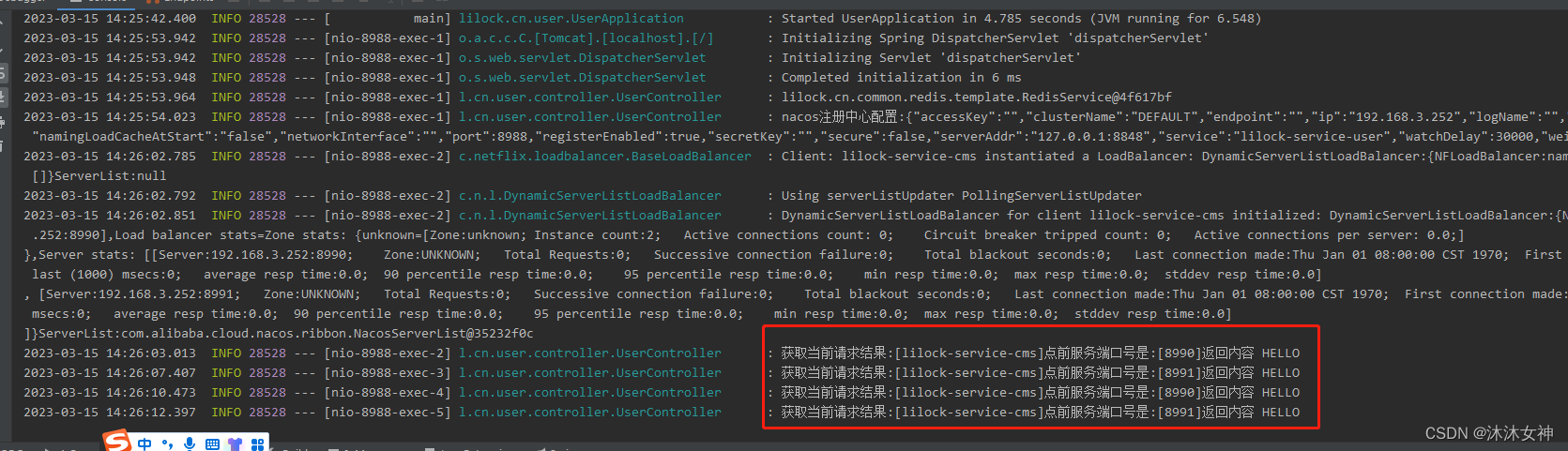
3.springcloud微服务架构搭建 之 《springboot自动装配ribbon》
1.springcloud微服务架构搭建 之 《springboot自动装配Redis》 2.springcloud微服务架构搭建 之 《springboot集成nacos注册中心》 ribbon工作原理自己网上百度,说的都很详细 目录 1.项目引入openfeign和ribbon配置 2.新建lilock-ribbon-spring-boot-starter 3…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
