【前端老赵的CSS简明教程】10-1 CSS预处理器和使用方法
大家好,欢迎来到本期前端课程。我是前端老赵,今天的课程将讲解CSS预处理器的概念和使用方法,希望能够帮助大家更好地进行前端开发。
CSS预处理器是什么?
CSS预处理器是一种将类似CSS的语言转换为CSS的工具。它们提供了许多额外的功能,如变量、嵌套、混入、函数等等。这些功能可以使CSS代码更易于维护和管理,同时也提高了开发效率。
CSS预处理器有好几种,如Sass、Less、Stylus、PostCSS等等。在实际项目中,我们可以根据自己的需求选择合适的CSS预处理器。
在本课程中,我们将重点介绍两种主流的CSS预处理器:Sass和Less。它们的使用方法类似,我们以Sass为例进行讲解。
首先,我们需要安装Sass。Sass可以通过使用npm进行安装。可以在终端窗口中输入以下命令进行安装:
Bash
npm install -g sass安装完成后,我们就可以在项目中使用Sass了。我们可以使用Sass编写一个.scss文件,然后将其编译为CSS文件。编译过程可以使用命令行进行,也可以使用自动化工具进行。这里我们使用命令行进行编译。可以在终端窗口中输入以下命令进行编译:
Bash
sass input.scss output.css其中,input.scss是我们编写的Sass文件,output.css是编译后生成的CSS文件。
下面,我们来看一段示例代码,它演示了如何使用Sass来定义变量和嵌套规则。
Sass (S
相关文章:

【前端老赵的CSS简明教程】10-1 CSS预处理器和使用方法
大家好,欢迎来到本期前端课程。我是前端老赵,今天的课程将讲解CSS预处理器的概念和使用方法,希望能够帮助大家更好地进行前端开发。 CSS预处理器是什么? CSS预处理器是一种将类似CSS的语言转换为CSS的工具。它们提供了许多额外的功能,如变量、嵌套、混入、函数等等。这些…...

BFC详解
1. 引言 在前端的布局手段中,一直有这么一个知识点,很多前端开发者都知道有它的存在,但是很多人也仅仅是知道它的存在而已,对它的作用也只是将将说得出来,可是却没办法说得非常的清晰。这个知识点,就是BFC…...
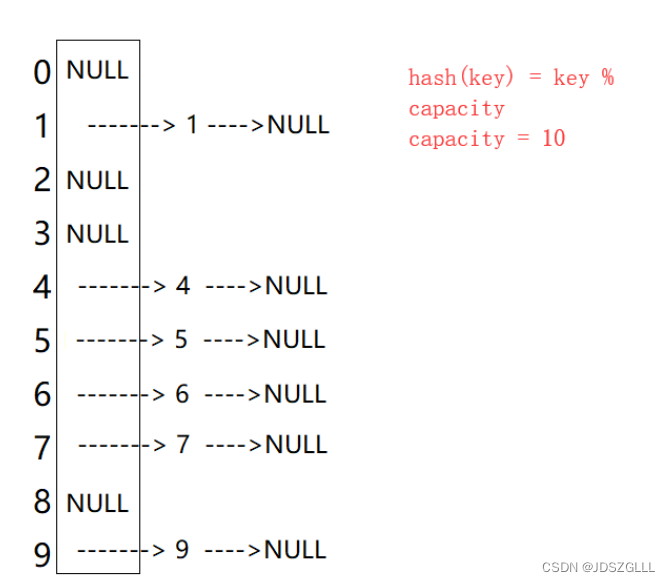
C++:哈希结构(内含unordered_set和unordered_map实现)
unordered系列关联式容器 在C98中,STL提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到$log_2 N$,即最差情况下需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好 的查询是ÿ…...
Java实现调用第三方相关接口(附详细思路)
目录1.0.简单版2.0.升级版2-1.call.timeout()怎么传入新的超时值2-2.timeout(10, TimeUnit.SECONDS)两个参数的意思,具体含义3.0.进阶版3-1.java.net.SocketTimeoutException: 超时如何解决4.0.终极版1.0.简单版 以下是一个使用 Java 实际请求“第三方”的简单示例代…...

基础数据结构:单链表
今天懒洋洋学习了关于基础数据结构有关单链表的相关操作,懒洋洋来这温习一下。一:单链表的定义链表定义:用链式存储的线性表统称为链表,即逻辑结构上连续,物理结构上不连续。链表分类:单链表、双链表、循环链表、静态链…...
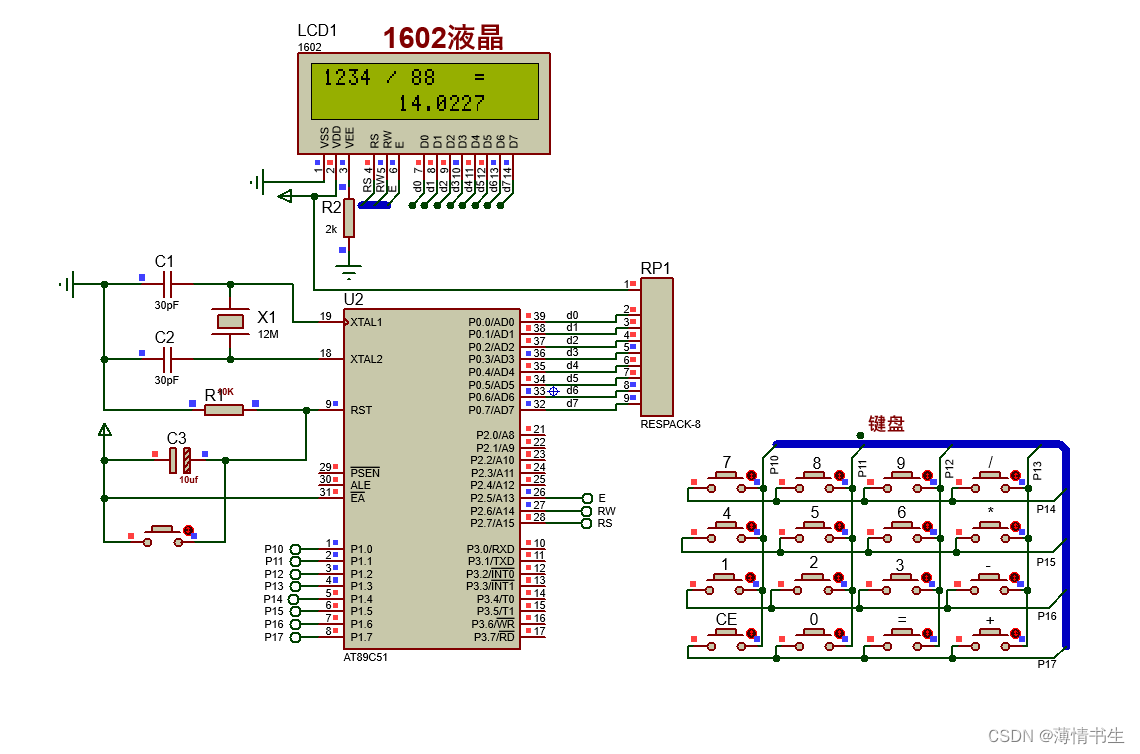
基于51单片机的智能计算器Protues仿真设计
目录 一、设计背景 二、实现功能 三、硬件设计 3.1 总体硬件设计 3.2 键盘电路的设计 3.3 显示电路的设计 四、仿真演示 五、源程序 一、设计背景 随着社会的发展,科学的进步,人们的生活水平在逐步的提高,尤其是微电子技术的发展&am…...

Pandas数据分析实战练习
Pandas数据分析实战练习 文章目录 Pandas数据分析实战练习一、读取Excel文件中的数据1、读取工号、姓名、时段、交易额这四列数据,使用默认索引,输出前10行数据2、读取第一个worksheet中所有列,跳过第1、3、5行,指定下标为1的列中数据为DataFrame的行索引标签二、筛选符合特…...
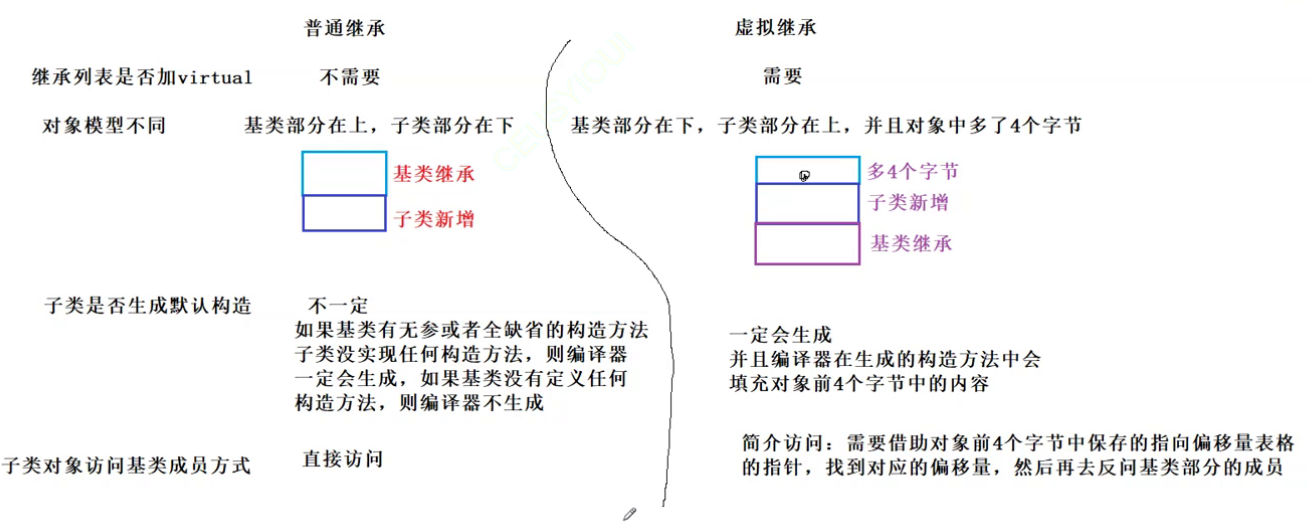
C++ 继承下(二篇文章学习继承所有知识点)
5.继承与友元友元关系不能继承,也就是说基类友元不能访问子类私有和保护成员 //验证友元不能继承 class B {friend void Print(); public:B(int b): _b(b){cout << "B()" << endl;}protected:int _b; };class D : public B { public:D(int b,…...
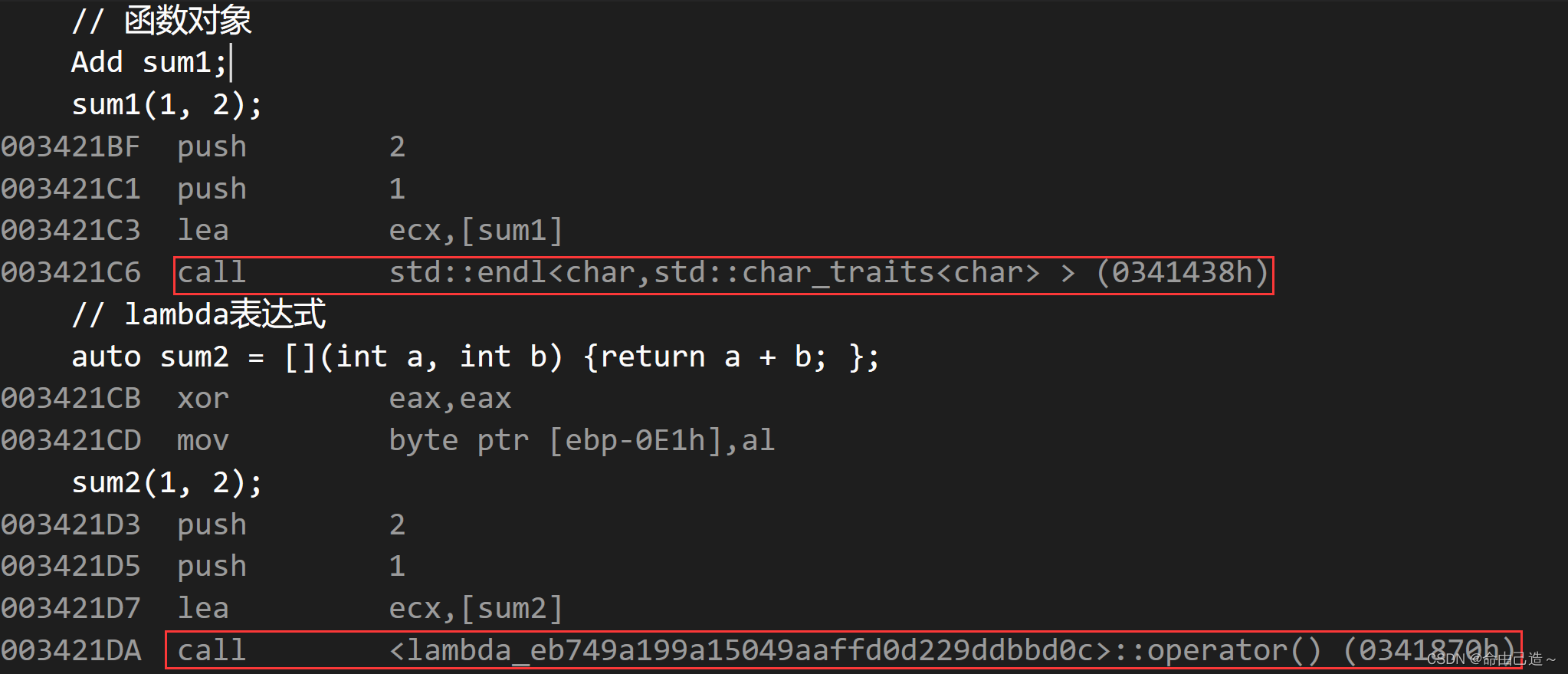
【C++】C++11新特性——类的改进|lambda表达式
文章目录一、类的改进1.1 默认生成1.2 移动构造函数1.3 移动赋值重载函数1.4 成员变量缺省值1.5 强制生成默认函数的关键字default1.6 禁止生成默认函数的关键字delete1.6.1 C98防拷贝1.6.1 C11防拷贝二、lambda表达式2.1 对比2.2 lambda表达式语法2.3 捕捉列表2.4 函数对象与l…...

C语言进阶(37) | 程序环境和预处理
目录 1.程序的翻译环境和执行环境 2.详解编译链接 2.1 翻译环境 2.2 编译本身也分为几个阶段: 2.3 运行环境 3.预处理详解 3.1预定符号 3.2 #define 3.3 #undef 3.4 命令行定义 3.5 条件编译 3.6 文件包含 了解重点: 程序的翻译环境程序的执行环境详解: C语言程…...

Golang每日一练(leetDay0005)
目录 13. 罗马数字转整数 Roman to Integer ★ 14. 最长公共前缀 Longest Common Prefix ★ 15. 三数之和 3Sum ★★★ 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 13. 罗马数字转…...
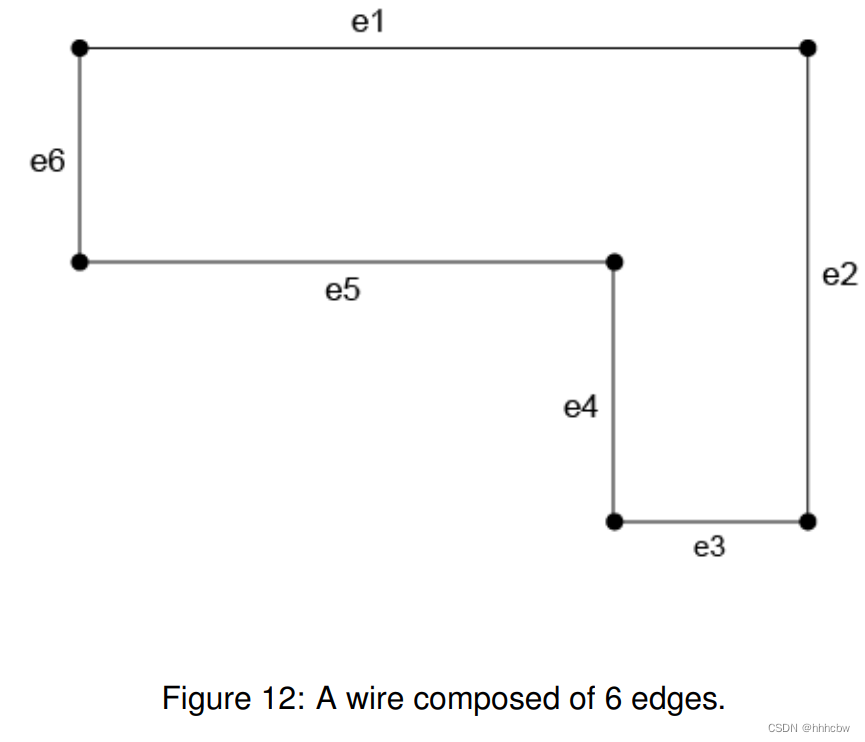
occt_modeling_data(一)——拓扑
下面是我基于opencascade英文文档中关于occt_modeling_data中Topology部分进行的翻译,英文好的还是建议直接看文档,部分我不肯定的地方我会附上英文原句。如发现有错误欢迎评论区留言。 OCCT Topolog允许用户访问和操纵物体的数据,且不需要处…...
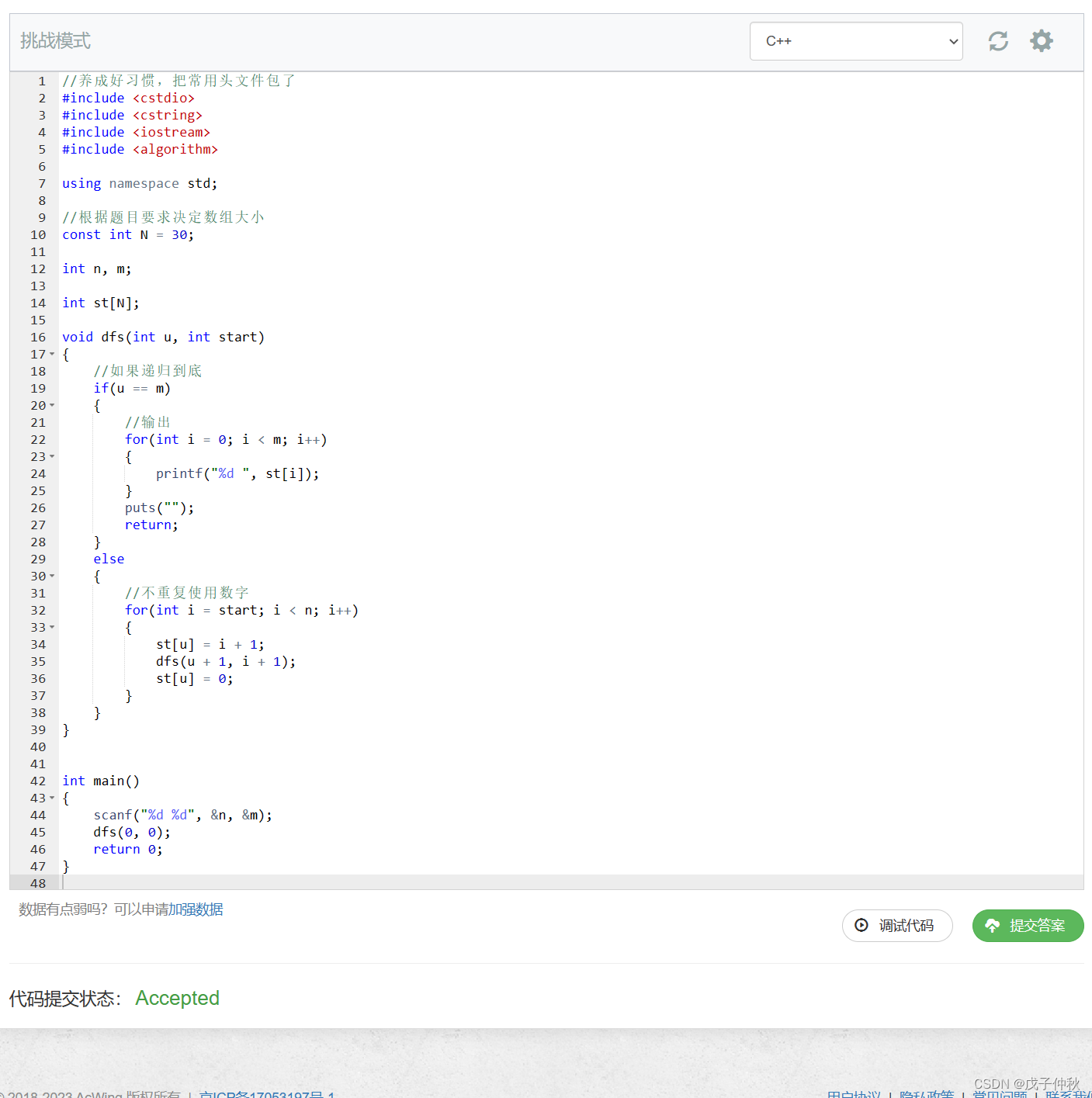
【AcWing】蓝桥杯备赛-深度优先搜索-dfs(3)
目录 写在前面: 题目:93. 递归实现组合型枚举 - AcWing题库 读题: 输入格式: 输出格式: 数据范围: 输入样例: 输出样例: 解题思路: 代码: AC &…...

宇宙最强-GPT-4 横空出世:最先进、更安全、更有用
文章目录前言一、准确性提升1.创造力2.视觉输入3.更长的上下文二、相比于ChatGPT有哪些提升1.GPT-4 的高级推理能力超越了 ChatGPT2.GPT-4 在多种测试考试中均优于 ChatGPT。三、研究团队在GPT-4模型都做了哪些改善1.遵循 GPT、GPT-2 和 GPT-3 的研究路径2.我们花了 6 个月的时…...
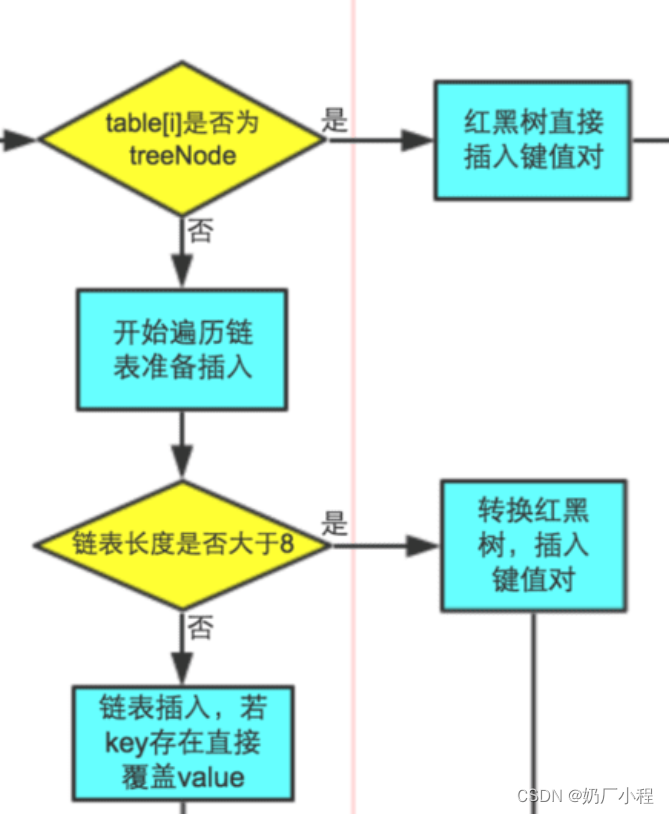
HashMap的实际开发使用
目 录 前言 一、HashMap是什么? 二、使用步骤 1.解析一下它实现的原理 编辑 2.实际开发使用 总结 前言 本章,只是大概记录一下hashMap的简单使用方法,以及理清一下hashMap的put方法的原理,以及get方法的原理。 一、Has…...

OpenCV入门(十三)快速学会OpenCV 12 图像梯度
OpenCV入门(十三)快速学会OpenCV 12 图像梯度1.Sobel算子1.1 计算x1.2 计算y1.3 计算xy2.Scharr算子2.1 计算x2.2 计算y2.3 计算xy3.Laplacian算子4.总结图像梯度计算的是图像变化的速度。对于图像的边缘部分,其灰度值变化较大,梯…...

软考:常见小题目计算题
01采购合同的类型采购合同主要包括总价类合同、成本补偿类合同、工料合同三大类合同。1、总价类合同此类合同为既定产品、服务或成果的采购设定一个总价。这种合同应在已明确定义需求,且不会出现重大范围变更的情况下使用。包括:(1࿰…...
【Linux】进程的程序替换
文章目录1. 程序替换1.创建子进程的目的是什么?2.了解程序是如何进行替换的3. 程序替换的基本原理当创建进程的时候,先有进程数据结构,还是先加载代码和数据?程序替换是整体替换,不是局部替换execl 返回值4. 替换函数1…...
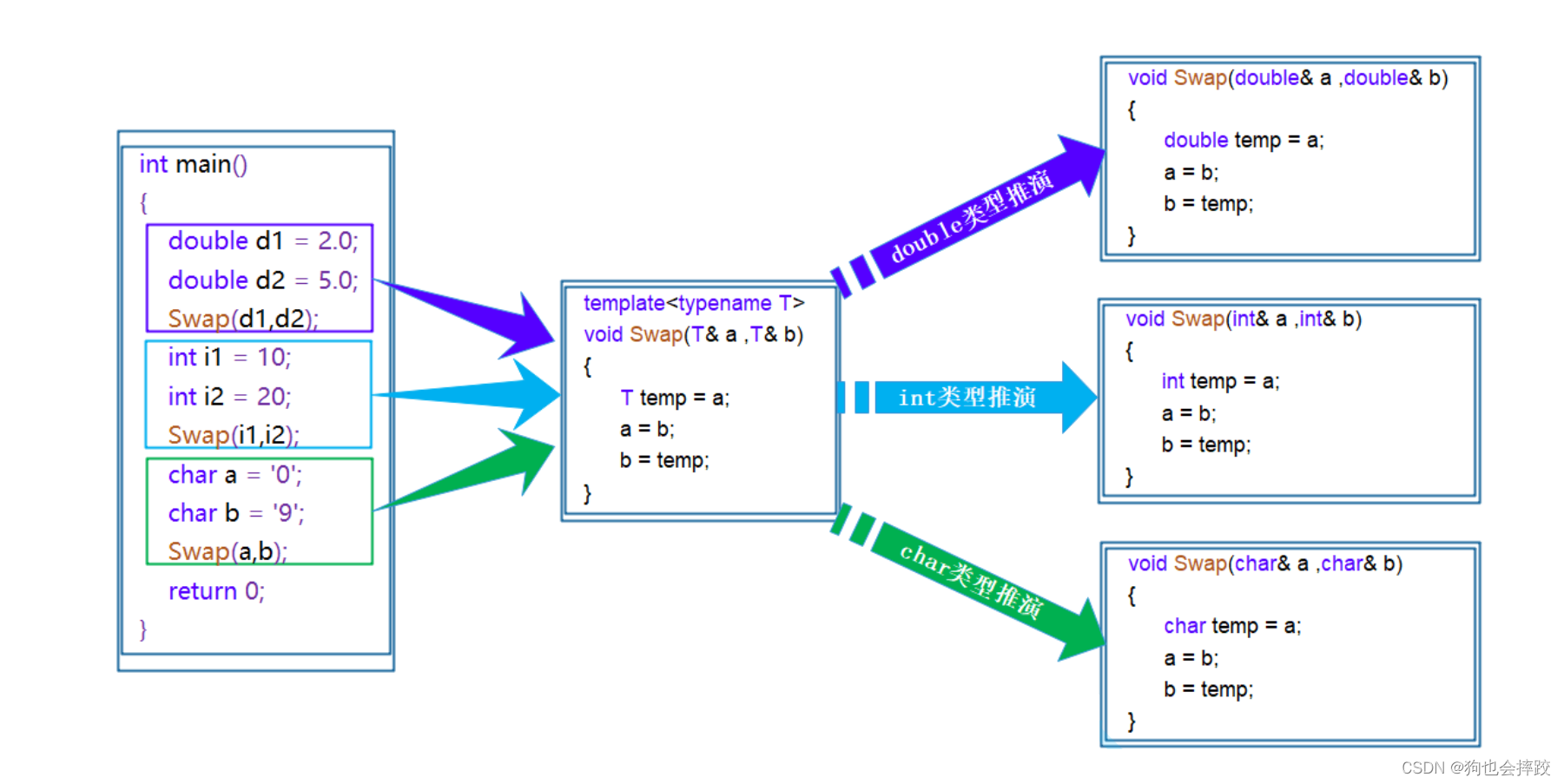
【C++】模板(上)
文章目录1、泛型编程2、函数模板函数模板的实例化模板参数的匹配原则3、 类模板类模板的实例化1、泛型编程 void Swap(int& left, int& right) {int temp left;left right;right temp; } void Swap(double& left, double& right) {double temp left;left …...
express框架利用formidable上传图片
express框架,在上传图片功能方面,用formidable里面的incomingform功能,很方便。很多功能都已经封装好了,非常好用,简单,不需要写更深层次的代码了。确实不错。 下面是我自己跟着黑马教程的博客系统的部分&…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
