(Java)试题 算法提高 约数个数
一、题目
(1)资源限制
内存限制:512.0MB
C/C++时间限制:1.0s
Java时间限制:3.0s
Python时间限制:5.0s
(2)输入
输入一个正整数N
(3)输出
N有几个约数
(4)样例输入
12
(5)样例输出
6
(6)样例说明
12的约数包括:1,2,3,4,6,12。共6个
二、原理与分析
(1)求约数的公式
(a1+1)*(a2+1)*(a3+1)*...*(ak+1)
(2)公式推理
- 任意一个数均可表示为以下形式(即分解质因数):
N=p1^a1*p2^a2*p3^a3*...*pk^ak
- 例如:
24 = 2^3*3^1 即p1=1,a1=0,p2=2,a2=3,p3=3,a3=1,p4=4,a4=0...
- 同样任意一个数的约数就可以表示为以下形式:
p1^b1,p2^b2,p3^b3*,...,pk^bk
-
我们可知从b1到bk的每一种取法,都对应着N的一个不同的约数
b1有[0,a1]种选法,即a1+1种选法
…
bk有[0,ak]种选法,即ak+1种选法 -
相乘可得
一共有(a1+1)*(a2+1)*(a3+1)*...*(ak+1)种选法,每种选法对应一个约数
- 求约数个数的问题被转化为了求从b1到bk的选法
即约数的个数 = (a1+1)*(a2+1)*(a3+1)*...*(ak+1)
(3)举例分析
- 例如:对180分解质因数可得
180 = (2^2)*(3^2)*(5^1)
- 根据公式可得约数个数为
(a1+1)*(a2+1)*(a3+1)*...*(ak+1)=(2+1)*(2+1)*(1+1)=18个
- 从根本上来说:
180 = (2^2)*(3^2)*(5^1)
以2为底,指数可以选择0,1,2,三种选法
以3为底,指数可以选择0,1,2,三种选法
以5为底,指数可以选择0,1,两种选法
那么约数一共就有
3*3*2=18种选法
(4)小知识
- int范围内的整数,约数个数最多的大概是1500个,有时可以用来快速验证答案
(5)HashMap
- 由于每一个p1和b1都是一一对应的,即底数和指数时一一对应的,我们可以用HashMap来存储
- 因此需要了解Map集合的相关知识:
Map集合是一种双列集合,每个元素包含两个数据。
Map集合的每个元素的格式:key=value(键值对元素)。
Map集合也被称为”键值对集合“
键和值一一对应,一个键对应一个值,整个集合的特点是由键决定的
HashMap:元素按照键是无序,不重复,无索引,值不做要求。(与Map体系一致)
getOrDefault(key, default):如果存在key, 则返回其对应的value, 否则返回给定的默认值
更加详细的关于HashMap的原理与使用可以看我的另一篇博客
暑期JAVA学习(13)Map集合体系
三、代码
import java.util.*;public class Main {//定义一个HashMap来对应存储所有项的底数与指数,一一对应,方便使用public static HashMap<Integer, Integer> primes = new HashMap<>();public static void main(String[] args) {Scanner sc = new Scanner(System.in);int x = sc.nextInt();//每个合数都可以写成几个质数相乘的形式,这几个质数就都叫做这个合数的质因数//此处用到的就是分解质因数的算法//用i遍历x的底数,若i为x的底数(即x%i==0),就把i对应的指数加一,即把map的value值加一//例如8=2^3,那么map中key为2的value值就一共会加3for (int i = 2; i <= x/i; i++) {while (x % i == 0){x = x/i;//getOrDefault(key, default)如果存在key, 则返回其对应的value, 否则返回给定的默认值//这一句用getOrDefault是防止NullPointerExceptionprimes.put(i, primes.getOrDefault(i, 0) + 1);}}//如果说x被所有小于根号x的质数因子除完后,还大于1,说明剩下的一定是那个大于根号x的质因子,直接输出即可 (例如11,43这样的数)//证明:一个数x中最多包含一个大于根号x的质数因子,很好证明,如果有两个大于根号x的质数因子那么这俩相乘就大于x了,反证法成立if (x > 1){primes.put(x, primes.getOrDefault(x, 0) + 1);}//result存储最终结果long result = 1;//用i遍历每一个指数//利用求约数个数的公式:(a1+1)*(a2+1)*(a3+1)*...*(ak+1)for (Integer i:primes.values()) {result = (result * (i + 1));}System.out.println(result);}
}
去注释版
import java.util.*;public class Main {public static HashMap<Integer, Integer> primes = new HashMap<>();public static void main(String[] args) {Scanner sc = new Scanner(System.in);int x = sc.nextInt();for (int i = 2; i <= x/i; i++) {while (x % i == 0){x = x/i;primes.put(i, primes.getOrDefault(i, 0) + 1);}}if (x > 1){primes.put(x, primes.getOrDefault(x, 0) + 1);}long result = 1;for (Integer i:primes.values()) {result = (result * (i + 1));}System.out.println(result);}
}相关文章:
试题 算法提高 约数个数)
(Java)试题 算法提高 约数个数
一、题目 (1)资源限制 内存限制:512.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s (2)输入 输入一个正整数N (3)输出 N有几个约数 &a…...

魔法反射--java反射初入门(基础篇)
👳我亲爱的各位大佬们好😘😘😘 ♨️本篇文章记录的为 java反射初入门 相关内容,适合在学Java的小白,帮助新手快速上手,也适合复习中,面试中的大佬🙉🙉🙉。 ♨️如果文章有…...
概率统计_协方差的传播 Covariance Propagation
1. 方差的传播 误差的传播是指分析在形如的关系中,参量误差(x)对变量误差(y)的影响有多大。误差的传播与函数的微分紧密相关,本质是在利用当Δ x 不大时,。 方差计算公式: X为变量,为总体均值,N为总体例数。求变量X与均值的差的平方再求平均值,即得到方差。方差…...
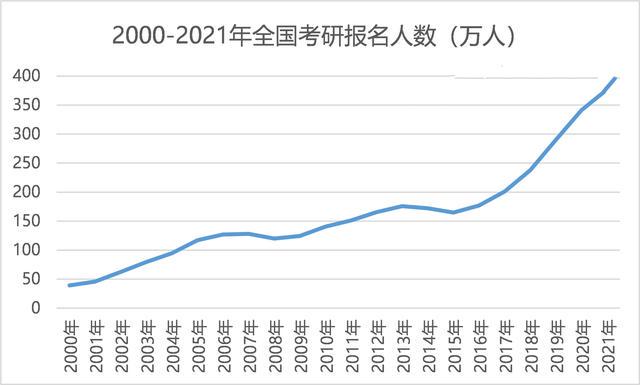
大学生考研的意义?
当我拿起笔头,准备写这个话题时,心里是非常难受的,因为看到太多的学生在最好的年华,在自由的大学本应该开拓知识,提升认知,动手实践,不断尝试和试错,不断历练自己跳出学生思维圈&…...
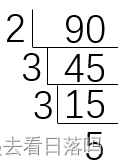
【C++笔试强训】第三十一天
🎇C笔试强训 博客主页:一起去看日落吗分享博主的C刷题日常,大家一起学习博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话:夜色难免微凉,前方必有曙光 🌞。 选择题 &#x…...
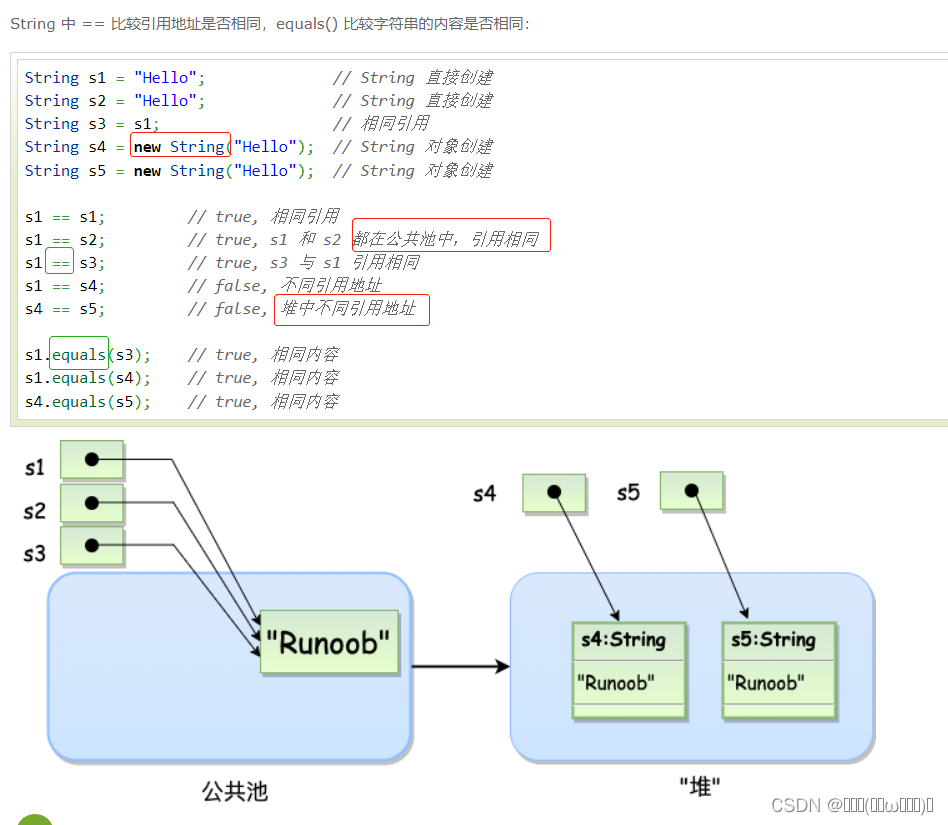
toString()、equals()是什么,为啥需要重写,多种方法来重写
https://m.runoob.com/java/java-object-class.html toString() 1.为什么会有toString 子类继承父类就可以使用父类所有非私有的属性的方法。 在Java中所有类都直接或者间接继承Object类,可以说只要是Object类里面定义的非私有的属性和方法,任何类都可…...

家装材料清单中会有哪些装饰材料?
在家居装修中,业主可以根据装修公司出具的材料清单去一一采购,这样不至于有遗漏,就算采用全包的方式,通过材料清单也可以大致了解当时房子装修所用的材料,补充自己的装修知识。下面跟随小编一起了解下房子装修材料中所…...

【C++初阶】6. CC++内存管理
1. C/C内存分布 我们先来看下面的一段代码和相关问题 int globalVar 1; static int staticGlobalVar 1; void Test() {static int staticVar 1;int localVar 1;int num1[10] { 1, 2, 3, 4 };char char2[] "abcd";const char* pChar3 "abcd";int* …...
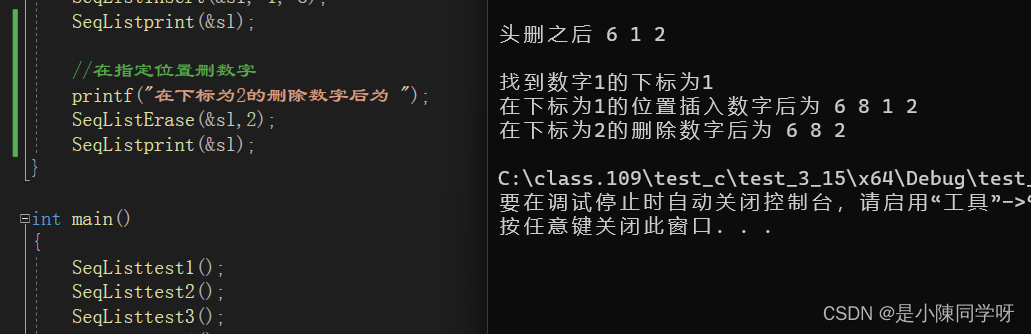
【数据结构】万字超详解顺序表(比细狗还细)
我这个人走得很慢,但是我从不后退。 ——亚伯拉罕林肯 目录 一.什么是线性表? 二.什么是顺序表? 三.接口函数的实现 1.创建工程 2.构造顺序表 3.初始化顺序表 3.初始化顺序表 4.顺序表的尾插 5.顺序…...

yolov5 剪枝、蒸馏、压缩、量化
文章大纲 剪枝推理优化YOLOv5 剪枝可能出现的问题参考文献与学习路径考察神经网络时期重要的激活函数sigmoid和tanh,它们有一个特点,即输入值较大或者较小的时候,其导数变得很小,而在训练阶段(详见1.2.3节),需要求取多个导数值,并将每层得到的导数值相乘,这样一旦层数…...

如何用python代码,更改照片尺寸,以及更换照片底色
前言 python浅浅替代ps?如何用代码来p证件照并且更换底色? 唉,有个小姐姐给我扔了张照片,叫我帮忙给她搞成证件照的尺寸还得换底色,她说自己忙的很 可惜电脑上没有ps只有pycharm,没得办法只能来试试看代…...

【pygame游戏】Python实现蔡徐坤大战篮球游戏【附源码】
前言 话说在前面,我不是小黑子~😏 本文章纯属技术交流~娱乐 前几天我获得了一个坤坤打篮球的游戏,也给大家分享一下吧~ 好吧,其实并不是这样的游戏,往下慢慢看吧。 准备工作 开发环境 Python版本:3.7.8 …...

通过指针引用字符串详解,以及字符指针变量和字符数组的比较
在平常的案例中已大量地使用了字符串,如在 printf函数中输出一个字符串。这些字符串都是以直接形式 (字面形式) 给出的,在一对双引号中包含若干个合法的字符。在本节中将介绍使用字符串的更加灵活方便的方法:通过指针引用字符串。 目录 一、…...
)
Vue基本整合(一)
NPM安装npm是node的包管理工具https://nodejs.org/en/脚手架安装npm i -g vue/clihttps://registry.npmjs.org/vue浏览器插件https://devtools.vuejs.org/guide/installation.html#chromehttps://chrome.google.com/webstore/detail/vuejs-devtools/nhdogjmejiglipccpnnnanhble…...

C++编程之 万能引用
万能引用是一种可以同时接受左值或右值的引用,它的形式是T&&,其中T是一个模板参数。万能引用不是C的一个新特性,而是利用了模板类型推导和引用折叠的规则来实现的功能。 模板类型推导 模板类型推导是指在调用一个模板函数时&#x…...
【JavaScript速成之路】JavaScript内置对象--数组对象
📃个人主页:「小杨」的csdn博客 🔥系列专栏:【JavaScript速成之路】 🐳希望大家多多支持🥰一起进步呀! 文章目录前言数组对象1,数组类型检测2,数组元素增删3,…...
【华为机试真题详解 Python实现】最差产品奖【2023 Q1 | 100分】
文章目录 前言题目描述输入描述输出描述示例 1题目解析参考代码前言 《华为机试真题详解》专栏含牛客网华为专栏、华为面经试题、华为OD机试真题。 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能…...

[算法] 二分查找
package com.guigu.search;import java.util.ArrayList; import java.util.Arrays;/*** author: guorui fu* versiion: 1.0* 二分查找 直接适用于已经排序完成的数组*/ public class BinarySearch {public static void main(String[] args) {int arr[] {1,8,8,89,101,1234};Ar…...

HTML面经
1.src与href的区别 src用于替换当前元素,如script标签,img标签等。当html解析到这些标签时,会暂停解析,将指定的资源下载下来,嵌入到所在位置内。href的话则是一个当前页面与引用资源之间的链接,如link标签…...

我的十年编程路 2021年篇
慢慢地,时光走过了8个年头,来到2021年。 站在2021年,回望8年的过往,没有大的起伏和波澜。或许是上天的眷顾,我的事业发展一直都很顺利。当然,弯路也走过一些,而且工作其实挺辗转的,…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
