人工智能算法工程师(中级)课程9-PyTorch神经网络之全连接神经网络实战与代码详解
大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(中级)课程9-PyTorch神经网络之全连接神经网络实战与代码详解。本文将给大家展示全连接神经网络与代码详解,包括全连接模型的设计、数学原理介绍,并从手写数字识别到猫狗识别实战演练。
文章目录
- 一、引言
- 二、全连接模型的设计
- 1. 神经元模型
- 2. 网络结构
- 三、全连接模型的参数计算
- 1. 前向传播
- 2. 反向传播
- 四、全连接模型实现手写数字识别
- 1. 数据准备
- 2. 模型构建
- 3. 代码实现
- 五、阶段实战:猫狗识别
- 1. 数据准备
- 2. 模型构建
- 3. 代码实现
- 六、数学原理详解
- 1. 激活函数
- 2. 损失函数
- 3. 优化算法
- 七、总结
一、引言
全连接神经网络(Fully Connected Neural Network,FCNN)是一种经典的神经网络结构,它在众多领域都有着广泛的应用。本文将详细介绍全连接神经网络的设计、参数计算及其在图像识别任务中的应用。通过本文的学习,读者将掌握全连接神经网络的基本原理,并能够实现手写数字识别和猫狗识别等实战项目。
二、全连接模型的设计
1. 神经元模型
全连接神经网络的基本单元是神经元,其数学表达式为:
f ( x ) = σ ( ∑ i = 1 n w i x i + b ) f(x) = \sigma(\sum_{i=1}^{n}w_ix_i + b) f(x)=σ(i=1∑nwixi+b)
其中, x x x 为输入向量, w w w 为权重向量, b b b 为偏置, σ \sigma σ 为激活函数。
2. 网络结构
全连接神经网络由输入层、隐藏层和输出层组成。每一层的神经元都与上一层的所有神经元相连,如图1所示。

三、全连接模型的参数计算
1. 前向传播
假设一个全连接神经网络共有 l l l层,第 k k k层的输入为 X ( k ) X^{(k)} X(k),输出为 Y ( k ) Y^{(k)} Y(k),则有:
Y ( k ) = σ ( W ( k ) X ( k ) + b ( k ) ) Y^{(k)} = \sigma(W^{(k)}X^{(k)} + b^{(k)}) Y(k)=σ(W(k)X(k)+b(k))
其中, W ( k ) W^{(k)} W(k) 和 b ( k ) b^{(k)} b(k) 分别为第 k k k层的权重和偏置。
2. 反向传播
全连接神经网络的参数更新通过反向传播算法实现。对于输出层,损失函数为:
L = 1 2 ( Y t r u e − Y p r e d ) 2 L = \frac{1}{2}(Y_{true} - Y_{pred})^2 L=21(Ytrue−Ypred)2
其中, Y t r u e Y_{true} Ytrue 为真实标签, Y p r e d Y_{pred} Ypred 为预测值。
根据链式法则,输出层的权重梯度为:
∂ L ∂ W ( l ) = ∂ L ∂ Y ( l ) ⋅ ∂ Y ( l ) ∂ Z ( l ) ⋅ ∂ Z ( l ) ∂ W ( l ) \frac{\partial L}{\partial W^{(l)}} = \frac{\partial L}{\partial Y^{(l)}} \cdot \frac{\partial Y^{(l)}}{\partial Z^{(l)}} \cdot \frac{\partial Z^{(l)}}{\partial W^{(l)}} ∂W(l)∂L=∂Y(l)∂L⋅∂Z(l)∂Y(l)⋅∂W(l)∂Z(l)
其中, Z ( l ) = W ( l ) X ( l ) + b ( l ) Z^{(l)} = W^{(l)}X^{(l)} + b^{(l)} Z(l)=W(l)X(l)+b(l)。
同理,可求得输出层的偏置梯度、隐藏层的权重梯度和偏置梯度。
四、全连接模型实现手写数字识别
1. 数据准备
使用MNIST数据集,包含60000个训练样本和10000个测试样本。
2. 模型构建
构建一个简单的全连接神经网络,包含一个输入层(784个神经元)、两个隐藏层(128个神经元)和一个输出层(10个神经元)。

3. 代码实现
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader# 定义模型
class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.model = nn.Sequential(nn.Flatten(),nn.Linear(28*28, 128),nn.ReLU(),nn.Linear(128, 128),nn.ReLU(),nn.Linear(128, 10),nn.Softmax(dim=1))def forward(self, x):return self.model(x)# 加载数据
transform = transforms.Compose([transforms.ToTensor()])
dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
dataloader = DataLoader(dataset, batch_size=32, shuffle=True)test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_dataloader = DataLoader(test_dataset, batch_size=32, shuffle=True)# 初始化模型和优化器
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = Net().to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)
criterion = nn.CrossEntropyLoss()# 训练模型
for epoch in range(5):for i, (images, labels) in enumerate(dataloader):images, labels = images.to(device), labels.to(device)optimizer.zero_grad()outputs = model(images)loss = criterion(outputs, labels)loss.backward()optimizer.step()# 评估模型
correct = 0
total = 0
with torch.no_grad():for images, labels in test_dataloader:images, labels = images.to(device), labels.to(device)outputs = model(images)_, predicted = torch.max(outputs.data, 1)total += labels.size(0)correct += (predicted == labels).sum().item()print('Accuracy of the network on the 10000 test images: %d %%' % (100 * correct / total))
五、阶段实战:猫狗识别
1. 数据准备
使用猫狗数据集,包含25000张猫和狗的图片。我们将猫和狗的照片放在目录’data/train’下。
2. 模型构建
构建一个全连接神经网络,包含一个输入层(64643个神经元)、三个隐藏层(256、128、64个神经元)和一个输出层(2个神经元)。
3. 代码实现
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader# 定义数据预处理
data_transforms = transforms.Compose([transforms.Resize((64, 64)),transforms.RandomRotation(40),transforms.RandomHorizontalFlip(),transforms.RandomVerticalFlip(),transforms.RandomAffine(0, translate=(0.2, 0.2), scale=(0.8, 1.2)),transforms.ToTensor(),
])# 加载数据
train_dataset = datasets.ImageFolder('data/train', transform=data_transforms)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)# 定义模型
class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.model = nn.Sequential(nn.Flatten(),nn.Linear(64*64*3, 256),nn.ReLU(),nn.Linear(256, 128),nn.ReLU(),nn.Linear(128, 64),nn.ReLU(),nn.Linear(64, 1),nn.Sigmoid())def forward(self, x):return self.model(x)# 初始化模型和优化器
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = Net().to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)
criterion = nn.BCELoss()# 训练模型
for epoch in range(15):for i, (images, labels) in enumerate(train_loader):images, labels = images.to(device), labels.float().unsqueeze(1).to(device)optimizer.zero_grad()outputs = model(images)loss = criterion(outputs, labels)loss.backward()optimizer.step()# 评估模型
# 假设有一个测试数据集的加载器叫做 validation_loader
correct = 0
total = 0
with torch.no_grad():for images, labels in validation_loader:images, labels = images.to(device), labels.to(device)outputs = model(images)predicted = (outputs > 0.5).float()total += labels.size(0)correct += (predicted == labels).sum().item()
print('Accuracy of the network on the test images: %d %%' % (100 * correct / total))
六、数学原理详解
1. 激活函数
激活函数用于引入非线性因素,使得神经网络能够学习和模拟复杂函数。常用的激活函数有:
- Sigmoid函数: σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1
- ReLU函数: R e L U ( x ) = max ( 0 , x ) ReLU(x) = \max(0, x) ReLU(x)=max(0,x)
- Softmax函数: s o f t m a x ( x ) i = e x i ∑ j e x j softmax(x)_i = \frac{e^{x_i}}{\sum_j e^{x_j}} softmax(x)i=∑jexjexi
2. 损失函数
损失函数用于衡量模型预测值与真实值之间的差异。常用的损失函数有:
- 均方误差(MSE): M S E ( y , y ^ ) = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 MSE(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2 MSE(y,y^)=n1∑i=1n(yi−y^i)2
- 交叉熵损失:对于二分类问题, C E ( y , y ^ ) = − y log ( y ^ ) − ( 1 − y ) log ( 1 − y ^ ) CE(y, \hat{y}) = -y\log(\hat{y}) - (1-y)\log(1-\hat{y}) CE(y,y^)=−ylog(y^)−(1−y)log(1−y^)
3. 优化算法
优化算法用于更新网络的权重和偏置,以最小化损失函数。常用的优化算法有:
- 梯度下降(Gradient Descent): w : = w − α ∂ L ∂ w w := w - \alpha \frac{\partial L}{\partial w} w:=w−α∂w∂L
- Adam优化器:结合了动量(Momentum)和自适应学习率(Adagrad)的优点。
七、总结
本篇文章从全连接神经网络的基本原理出发,介绍了全连接模型的设计、参数计算以及如何实现手写数字识别和猫狗识别。通过配套的完整可运行代码,读者可以更好地理解全连接神经网络的实现过程。在实际应用中,全连接神经网络虽然已被卷积神经网络(CNN)等更先进的网络结构所取代,但其基本原理仍然是深度学习领域的重要基石。希望本文能帮助读者深入掌握全连接神经网络,并为后续学习打下坚实的基础。
相关文章:

人工智能算法工程师(中级)课程9-PyTorch神经网络之全连接神经网络实战与代码详解
大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(中级)课程9-PyTorch神经网络之全连接神经网络实战与代码详解。本文将给大家展示全连接神经网络与代码详解,包括全连接模型的设计、数学原理介绍,并从手写数字识别到猫狗识…...

UDP网络通信(发送端+接收端)实例 —— Python
简介 在网络通信编程中,用的最多的就是UDP和TCP通信了,原理这里就不分析了,网上介绍也很多,这里简单列举一下各自的优缺点和使用场景 通信方式优点缺点适用场景UDP及时性好,快速视网络情况,存在丢包 与嵌入…...
:缩放点积注意力机制)
从零开始实现大语言模型(五):缩放点积注意力机制
1. 前言 缩放点积注意力机制(scaled dot-product attention)是OpenAI的GPT系列大语言模型所使用的多头注意力机制(multi-head attention)的核心,其目标与前文所述简单自注意力机制完全相同,即输入向量序列 x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n x...

PTA 7-15 希尔排序
本题目要求读入N个整数,采用希尔排序法进行排序,采用增量序列{5,3,1},输出完成增量5和增量3后的5子排序和3子排序结果。 输入格式: 输入不超过100的正整数N和N个整数(空格分隔)。 输出格式: …...

【密码学】分组密码的设计原则
分组密码设计的目标是在密钥控制下,从一个巨大的置换集合中高效地选取一个置换,用于加密给定的明文块。 一、混淆原则 混淆原则是密码学中一个至关重要的概念,由克劳德香农提出。混淆原则就是将密文、明文、密钥三者之间的统计关系和代数关系…...

深入解析【C++ list 容器】:高效数据管理的秘密武器
目录 1. list 的介绍及使用 1.1 list 的介绍 知识点: 小李的理解: 1.2 list 的使用 1.2.1 list 的构造 知识点: 小李的理解: 代码示例: 1.2.2 list 迭代器的使用 知识点: 小李的理解࿱…...

NFS服务器、autofs自动挂载综合实验
综合实验 现有主机 node01 和 node02,完成如下需求: 1、在 node01 主机上提供 DNS 和 WEB 服务 2、dns 服务提供本实验所有主机名解析 3、web服务提供 www.rhce.com 虚拟主机 4、该虚拟主机的documentroot目录在 /nfs/rhce 目录 5、该目录由 node02 主机…...

自动驾驶事故频发,安全痛点在哪里?
大数据产业创新服务媒体 ——聚焦数据 改变商业 近日,武汉城市留言板上出现了多条关于萝卜快跑的投诉,多名市民反映萝卜快跑出现无故停在马路中间、高架上占最左道低速行驶、转弯卡着不动等情况,导致早晚高峰时段出现拥堵。萝卜快跑是百度 A…...

SpringSecurity框架【认证】
目录 一. 快速入门 二. 认证 2.1 登陆校验流程 2.2 原理初探 2.3 解决问题 2.3.1 思路分析 2.3.2 准备工作 2.3.3 实现 2.3.3.1 数据库校验用户 2.3.3.2 密码加密存储 2.3.3.3 登录接口 2.3.3.4 认证过滤器 2.3.3.5 退出登录 Spring Security是Spring家族中的一个…...

python安全脚本开发简单思路
文章目录 为什么选择python作为安全脚本开发语言如何编写人生第一个安全脚本开发后续学习 为什么选择python作为安全脚本开发语言 易读性和易维护性:Python以其简洁的语法和清晰的代码结构著称,这使得它非常易于阅读和维护。在安全领域,代码…...

WPF学习(4) -- 数据模板
一、DataTemplate 在WPF(Windows Presentation Foundation)中,DataTemplate 用于定义数据的可视化呈现方式。它允许你自定义如何展示数据对象,从而实现更灵活和丰富的用户界面。DataTemplate 通常用于控件(如ListBox、…...

GuLi商城-商品服务-API-品牌管理-JSR303分组校验
注解:@Validated 实体类: package com.nanjing.gulimall.product.entity;import com.baomidou.mybatisplus.annotation.TableId; import com.baomidou.mybatisplus.annotation.TableName; import com.nanjing.common.valid.ListValue; import com.nanjing.common.valid.Updat…...

PyTorch DataLoader 学习
1. DataLoader的核心概念 DataLoader是PyTorch中一个重要的类,用于将数据集(dataset)和数据加载器(sampler)结合起来,以实现批量数据加载和处理。它可以高效地处理数据加载、多线程加载、批处理和数据增强…...
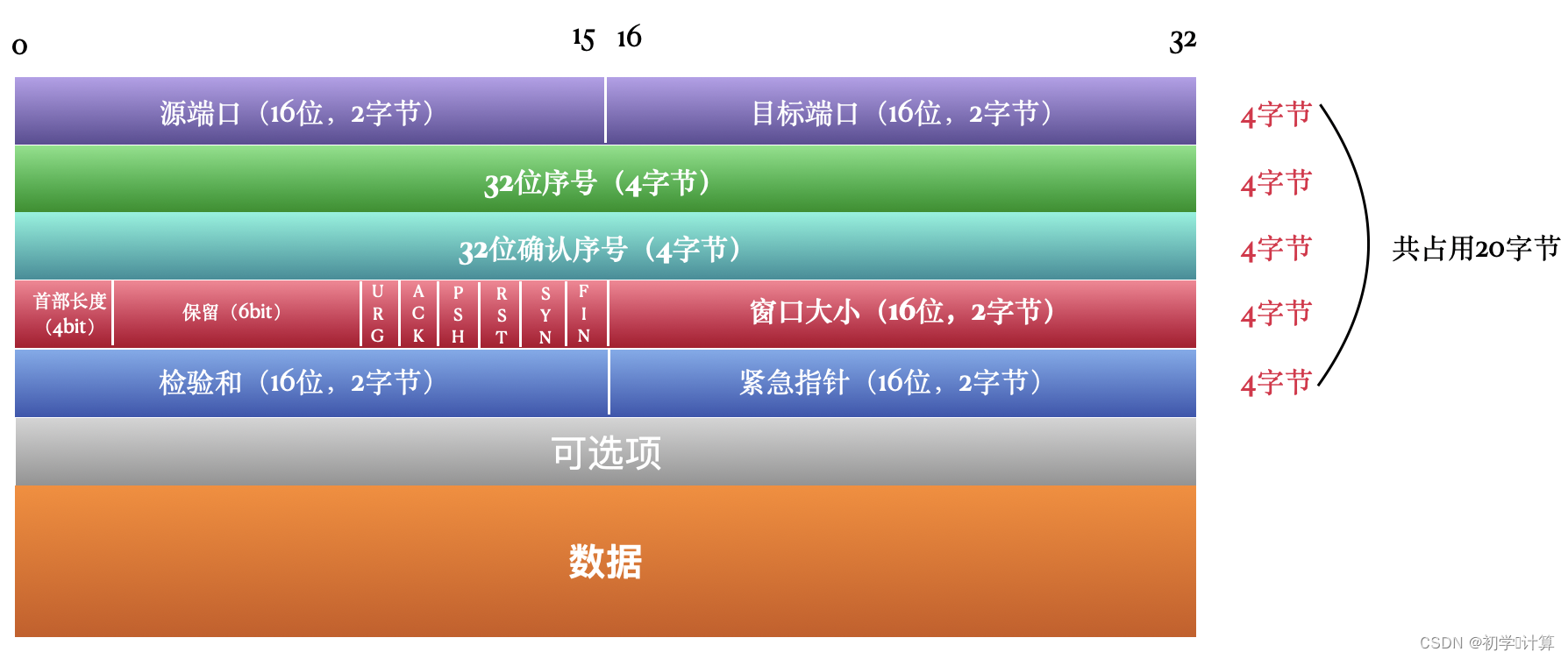
TCP传输控制协议二
TCP 是 TCP/IP 模型中的传输层一个最核心的协议,不仅如此,在整个 4 层模型中,它都是核心的协议,要不然模型怎么会叫做 TCP/IP 模型呢。 它向下使用网络层的 IP 协议,向上为 FTP、SMTP、POP3、SSH、Telnet、HTTP 等应用…...

【学习笔记】无人机(UAV)在3GPP系统中的增强支持(五)-同时支持无人机和eMBB用户数据传输的用例
引言 本文是3GPP TR 22.829 V17.1.0技术报告,专注于无人机(UAV)在3GPP系统中的增强支持。文章提出了多个无人机应用场景,分析了相应的能力要求,并建议了新的服务级别要求和关键性能指标(KPIs)。…...
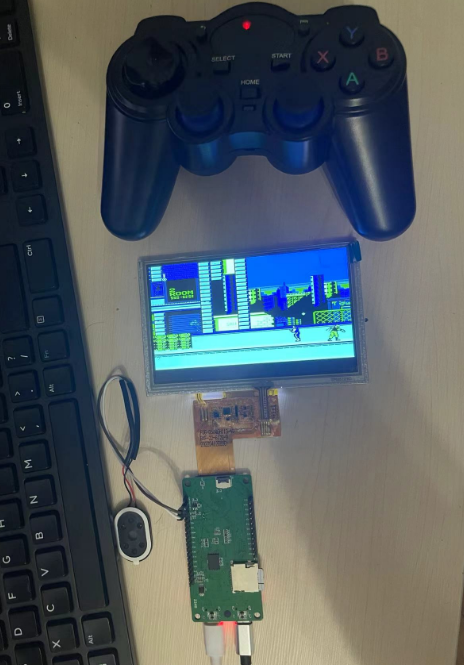
使用F1C200S从零制作掌机之debian文件系统完善NES
一、模拟器源码 源码:https://files.cnblogs.com/files/twzy/arm-NES-linux-master.zip 二、文件系统 文件系统:debian bullseye 使用builtroot2018构建的文件系统,使用InfoNES模拟器存在bug,搞不定,所以放弃&…...

Vue 3 与 TypeScript:最佳实践详解
大家好,我是CodeQi! 很多人问我为什么要用TypeScript? 因为 Vue3 喜欢它! 开个玩笑... 在我们开始探索 Vue 3 和 TypeScript 最佳实践之前,让我们先打个比方。 如果你曾经尝试过在没有 GPS 的情况下开车到一个陌生的地方,你可能会知道那种迷失方向的感觉。 而 Typ…...

PyMysql error : Packet Sequence Number Wrong - got 1 expected 0
文章目录 错误一错误原因解决方案 错误二原因解决方案 我自己知道的,这类问题有两类原因,两种解决方案。 错误一 错误原因 pymysql的主进程启动的connect无法给子进程中使用,所以读取大批量数据时最后容易出现了此类问题。 解决方案 换成…...
MVC 生成验证码
在mvc 出现之前 生成验证码思路 在一个html页面上,生成一个验证码,在把这个页面嵌入到需要验证码的页面中。 JS生成验证码 <script type"text/javascript">jQuery(function ($) {/**生成一个随机数**/function randomNum(min, max) {…...

OSPF.综合实验
1、首先将各个网段基于172.16.0.0 16 进行划分 1.1、划分为4个大区域 172.16.0.0 18 172.16.64.0 18 172.16.128.0 18 172.16.192.0 18 四个网段 划分R4 划分area2 划分area3 划分area1 2、进行IP配置 如图使用配置指令进行配置 ip address x.x.x.x /x 并且将缺省路由…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
