【Python 项目】类鸟群:仿真鸟群
类鸟群:仿真鸟群
仔细观察一群鸟或一群鱼,你会发现,虽然群体由个体生物组成,但该群体作为一个整体似乎有它自己的生命。鸟群中的鸟在移动、飞越和绕过障碍物时,彼此之间相互定位。受到打扰或惊吓时会破坏编队,但随后重新集结,仿佛被某种更大的力量控制。
1986年,Craig Reynolds创造鸟类群体行为的一种逼真模拟,称为“类鸟群(Boids)”模型。关于类鸟群模型,值得注意的是,只有 3 个简单的规则控制着群体中个体间的相互作用,但该模型产生的行为类似于真正的鸟群。类鸟群模型被广泛研究,甚至被用来制作群体的计算机动画,如电影“蝙蝠侠归来(1992)”中的行军企鹅。
本项目将利用 Reynolds 的 3 个规则,创建一个类鸟群,模拟 N 只鸟的群体行为,并画出随着时间的推移,它们的位置和运动方向。我们还会提供一个方法,向鸟群中添加一只鸟,以及一种驱散效果,可以用于研究群体的局部干扰效果。类鸟群被称为“N 体模拟”,因为它模拟了 N 个粒子的动态系统,彼此之间施加作用力。
工作原理
模拟类鸟群的三大核心规则如下:
分离:保持类鸟个体之间的最小距离;
列队:让每个类鸟个体指向其局部同伴的平均移动方向;
内聚:让每个类鸟个体朝其局部同伴的质量中心移动。
类鸟群模拟也可以添加其他规则,如避开障碍物,或受到打扰时驱散鸟群,在随后的小节中我们将会探讨这些。这个版本的类鸟群在模拟的每一步中,实现了这些核心规则。
对于群体中的所有类鸟个体,做以下几件事:
- 应用三大核心规则;
- 应用所有附加规则;
- 应用所有边界条件。
- 更新类鸟个体的位置和速度。
- 绘制新的位置和速度。
如你所见,这些简单的规则创造了一个鸟群,它具有演变的复杂行为。
所需模块
下面是该模拟要用到的 Python 工具:
- numpy 数组,用于保存类鸟群的位置和速度;
- matplotlib 库,用于生成类鸟群动画;
- argparse,用于处理命令行选项;
- scipy.spatial.distance 模块,包含一些非常简洁的方法,计算点之间的距离。
代码
首先,要计算类鸟群的位置和速度。接下来,要为模拟设置边界条件,看看如何绘制类鸟群,并实现前面讨论的类鸟群模拟规则。最后,我们会为模拟添加一些有趣的事件,即添加一些类鸟个体和驱散类鸟群。
计算类鸟群的位置和速度
类鸟群仿真需要从 numpy 数组取得信息,计算每一步中类鸟群个体的位置和速度。模拟开始时,将所有类鸟群个体大致放在屏幕中央,速度设置为随机的方向。
import math
import numpy as npwidth, height = 640, 480pos = [width/2.0, height/2.0] + 10*np.random.rand(2*N).reshape(N, 2)
angles = 2*math.pi*np.random.rand(N)
vel = np.array(list(zip(np.sin(angles), np.cos(angles))))
开始在第一行导入 math 模块,用于接下来的计算。在第二行,将 numpy 库导入为 np(少一些录入)。然后,设置屏幕上模拟窗口的宽度和高度。在第四行,创建一个 numpy 数组 pos,对窗口中心加上 10 个单位以内的随机偏移。代码np.random.rand(2 * N)创建了一个一维数组,包含范围在[0,1]的 2N 个随机数。然后 reshape()调用将它转换成二维数组的形状(N,2),它将用于保存类鸟群个体的位置。也要注意,numpy 的广播规则在这里生效:1×2 的数组加到 N×2 的数组的每个元素上。
接下来,用以下方法,创建随机单位速度矢量数组(这些都是模为 1.0 的矢量,指向随机的方向):给定一个角度 t,数字对(cos(t), sin(t))位于半径为 1.0 的圆上,中心在原点(0, 0)。如果从原点到圆上的一点画一条线,就得到一个单位矢量,它取决于角度 A。如果随机选择角度 A,就得到一个随机速度矢量。下图展示了这个方案。

在第五行,生成一个数组,包含 N 个随机角度,范围在[0, 2pi],在第六行,用前面讨论的随机向量方法生成一个数组,并用内置的 zip()方法将坐标分组。
设置边界条件
鸟儿飞翔在无际的天空,但类鸟群必须在有限的空间中运动。要创建这个空间,就要创建边界条件,在这个例子中,我们采用“平铺小块边界条件”。
将类鸟群模拟想象成发生在一个平铺的空间:如果类鸟群个体离开一个小块,它将从相反的方向进入到相同的小块。环形边界条件和小块边界条件之间的主要区别是,类鸟群模拟不会发生在离散的网格上,而是在一个连续区域移动。下图展示了这些小块边界条件的样子。请看下图中间的小块。飞出右侧的鸟儿正进入右边的小块,但该边界条件确保它们实际上通过平铺在左边的小块,又回到了中心的小块。在顶部和底部的小块,可以看到同样的事情发生。

下面是如何为类鸟群模拟实现平铺小块边界条件:
def applyBC(self):"""apply boundary conditions"""deltaR = 2.0for coord in self.pos:if coord[0] > width + deltaR:coord[0] = - deltaRif coord[0] < - deltaR:coord[0] = width + deltaRif coord[1] > height + deltaR:coord[1] = - deltaRif coord[1] < - deltaR:coord[1] = height + deltaR
在第五行,如果 x 坐标比小块的宽度大,则将它设置回小块的左侧边缘。该行中的 deltaR 提供了一个微小的缓冲区,它允许类鸟群个体开始从相反方向回来之前,稍稍移出小块之外一点,从而产生更好的视觉效果。在小块的左侧、顶部和底部边缘执行类似的检查。
绘制类鸟群
要生成动画,需要知道类鸟群个体的位置和速度,并有办法在每个时间步骤中表示位置和运动方向。
绘制类鸟群个体的身体和头部
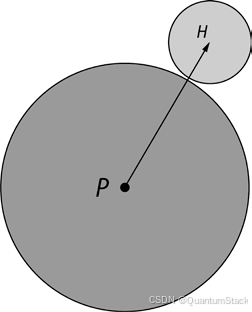
为了生成类鸟群动画,我们用 matplotlib 和一点小技巧来绘制位置和速度。将每个类鸟群个体画成两个圆,如下图所示。较大的圆代表身体,较小的圆表示头部。点 P 是身体的中心,H 是头部的中心。根据公式 H = P + k × V 来计算 H 的位置,其中 V 是类鸟群个体的速度,k 是常数。在任何给定时间,类鸟群个体的头指向运动的方向。这指明了类鸟群个体的移动方向,比只画身体更好。
在下面的代码片段中,利用 matplotlib,用圆形标记画出类鸟群个体的身体。
fig = plt.figure()
ax = plt.axes(xlim=(0, width), ylim=(0, height))pts, = ax.plot([], [], markersize=10, c='k', marker='o', ls='None')
beak, = ax.plot([], [], markersize=4, c='r', marker='o', ls='None')
anim = animation.FuncAnimation(fig, tick, fargs=(pts, beak, boids),interval=50)
在第三和第四行分别为类鸟群个体的身体(pts)和头部(beak)标记设置大小和形状。在第五行为动画窗口添加鼠标按钮事件。既然知道了如何绘制身体和喙,让我们看看如何更新它们的位置。
更新类鸟群个体的位置
动画开始后,需要更新身体和头的位置,它指明了类鸟群个体移动的方向。用以下代码来实现:
vec = self.pos + 10*self.vel/self.maxVel
beak.set_sdata(vec.rehape(2*self.N)[::2], vec.reshape(2*self.N)[1::2])
在第一行,计算头部的位置,即在速度(vel)的方向上增加 10 个单位的位移。该位移确定了喙和身体之间的距离。在第二行,用头部位置的新值来更新(reshape)matplotlib 的轴(set_data)。[::2]从速度列表中选出偶数元素(x 轴的值),[1::2]选出奇数元素(Y 轴的值)。
应用类鸟群规则
现在,要在 Python 中实现类鸟群的 3 个规则。我们用“numpy 的方式”来完成这件事,避免循环并利用高度优化的 numpy 方法。
import numpy as np
from scipy.spatial.distance import squareform, pdist, cdistdef test2(pos, radius):# get distance matrixdistMatrix = squareform(pdist(pos))# apply thresholdD = distMatrix < radius# compute velocityvel = pos*D.sum(axis=1).reshape(N, 1) - D.dot(pos)return vel
在第五行,用 squareform()和 pdist()方法(在 scipy 库中定义),来计算一组点之间两两的距离(从数组中任意取两点,计算距离,然后针对所有可能的两点对这么做)。
squareform()方法给出一个 3×3 矩阵,其中项 Mij 给出了点 Pi和 Pj 之间的距离。接下来,在第七行,基于距离筛选这个矩阵。
在第九行的方法有点复杂。D.sum()方法按列对矩阵中的 True 值求和。reshape 是必需的,因为和是 N 个值的一维数组(形如(N,)),而你希望它形如(N,1),这样它就能够与位置数组相乘。D.dot()就是矩阵和位置矢量的点积(乘法)。
下面的方法利用前面讨论的 numpy 技术,应用类鸟群的 3 个规则:
def applyRules(self):# apply rule #1: SeparationD = distMatrix < 25.0vel = self.pos*D.sum(axis=1).reshape(self.N, 1) - D.dot(self.pos)#应用分离规则时,每个个体都被“推离”相邻个体一定距离#计算出的速度被限制在某个最大值以内self.limit(vel, self.maxRuleVel)# distance threshold for alignment (different from separation)D = distMatrix < 50.0# apply rule #2: Alignmentvel2 = D.dot(self.vel)#应用列队规则时,50 个单位的半径内,所有相邻个体的速度之和限制为一个最大值 self.limit(vel2, self.maxRuleVel)vel += vel2;# apply rule #3: Cohesionvel3 = D.dot(self.pos) - self.pos#为每个个体增加一个速度矢量,它指向一定半径内相邻个体的重心或几何中心 self.limit(vel3, self.maxRuleVel)vel += vel3return vel
添加个体
类鸟群模拟的核心规则会导致类鸟群展示出群聚行为。但是,让我们在模拟过程中添加一个个体,看看表现如何,让事情变得更有趣。
下面的代码创建一个鼠标事件,让你点击鼠标左键添加一个个体。个体将出现在光标的位置,具有随机指定的速度
# 用 mpl_connect()方法向 matplotlib 画布添加一个按钮按下事件
cid = fig.canvas.mpl_connect('button_press_event', buttonPress)
现在,为了处理鼠标事件,实际创建类鸟群个体,添加以下代码:
def buttonPress(self, event):"""event handler for matplotlib button presses"""#确保鼠标事件是左键点击if event.button is 1:#将(event.xdata,event.ydata)给出的鼠标位置添加到类鸟群的位置数组 self.pos = np.concatenate((self.pos, np.array([[event.xdata, event.ydata]])), axis=0)# 将一个随机速度矢量添加到类鸟群的速度数组,并将类鸟群的计数增加 1angles = 2*math.pi*np.random.rand(1)v = np.array(list(zip(np.sin(angles), np.cos(angles))))self.vel = np.concatenate((self.vel, v), axis=0)self.N += 1
驱散类鸟群
3 个模拟规则保持类鸟群在移动时成为一个群体。但是,群体受到惊扰时,会发生什么?为了模拟这种情况,可以引入一种“驱散”效果:如果在用户界面(UI)窗口中单击右键,群体就会分散。你可以认为这是群体面对突然出现的捕食者的反应,或突然出现一声巨响惊吓了鸟群。下面是实现该效果的一种方式,它作为buttonPress()方法的延续:
# 检查鼠标按键是否是右键单击事件elif event.button is 3:# 改变每个个体的速度,在干扰出现的点(即点击鼠标的位置)的相反的方向上增加一个分量 self.vel += 0.1*(self.pos - np.array([[event.xdata, event.ydata]]))
最初,类鸟群将飞离该点,但你会看到,3 个规则胜出,类鸟群将作为群体再次会聚。
命令行参数
下面是类鸟群程序如何处理命令行参数:
parser = argparse.ArgumentParser(description="Implementing CraigReynolds's Boids...")# add arguments
parser.add_argument('--num-boids', dest='N', required=False)
args = parser.parse_args()# set the initial number of boids
N = 100
if args.N:N = int(args.N)# create boids
boids = Boids(N)
Boids 类
接下来看看 Boids 类,它代表了模拟。
class Boids:"""class that represents Boids simulation"""def __init__(self, N):"""initialize the Boid simulation"""# 初始化位置和速度数组self.pos = [width/2.0, height/2.0] + 10*np.random.rand(2*N).reshape(N, 2)# normalized random velocitiesangles = 2*math.pi*np.random.rand(N)self.vel = np.array(list(zip(np.sin(angles), np.cos(angles))))self.N = N # minimum distance of approachself.minDist = 25.0# maximum magnitude of velocities calculated by "rules"self.maxRuleVel = 0.03# maximum magnitude of the final velocityself.maxVel = 2.0
Boid 类处理初始化,更新动画,并应用规则。
boids.tick()在每个时间步骤被调用,以便更新动画,如下所示:
def tick(frameNum, pts, beak, boids):#print frameNum"""update function for animation"""boids.tick(frameNum, pts, beak)return pts, beak
我们还需要一种方法来限制某些矢量的值。否则,速度将在每个时间步骤无限制地增加,模拟将崩溃。
def limitVec(self, vec, maxVal):"""limit the magnitude of the 2D vector"""mag = norm(vec)if mag > maxVal:vec[0], vec[1] = vec[0]*maxVal/mag, vec[1]*maxVal/mag#限制了数组中的值,采用模拟规则计算出的值def limit(self, X, maxVal):"""limit the magnitude of 2D vectors in array X to maxValue"""for vec in X:self.limitVec(vec, maxVal)
完整代码
下面是类鸟群模拟的完整程序:
import sys, argparse
import math
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from scipy.spatial.distance import squareform, pdist, cdist
from numpy.linalg import normwidth, height = 640, 480class Boids:"""class that represents Boids simulation"""def __init__(self, N):"""initialize the Boid simulation"""# 初始化位置和速度数组self.pos = [width/2.0, height/2.0] + 10*np.random.rand(2*N).reshape(N, 2)# normalized random velocitiesangles = 2*math.pi*np.random.rand(N)self.vel = np.array(list(zip(np.sin(angles), np.cos(angles))))self.N = N # minimum distance of approachself.minDist = 25.0# maximum magnitude of velocities calculated by "rules"self.maxRuleVel = 0.03# maximum magnitude of the final velocityself.maxVel = 2.0def tick(self, frameNum, pts, beak):#print frameNum"""update function for animation"""self.distMatrix = squareform(pdist(self.pos))self.vel += self.applyRules()self.limit(self.vel, self.maxVel)self.pos += self.velself.applyBC()pts.set_data(self.pos.reshape(2*self.N)[::2], self.pos.reshape(2*self.N)[1::2])vec = self.pos + 10*self.vel/self.maxVelbeak.set_data(vec.reshape(2*self.N)[::2], vec.reshape(2*self.N)[1::2])def limitVec(self, vec, maxVal):"""limit the magnitude of the 2D vector"""mag = norm(vec)if mag > maxVal:vec[0], vec[1] = vec[0]*maxVal/mag, vec[1]*maxVal/mag#限制了数组中的值,采用模拟规则计算出的值def limit(self, X, maxVal):"""limit the magnitude of 2D vectors in array X to maxValue"""for vec in X:self.limitVec(vec, maxVal)def applyBC(self):"""apply boundary conditions"""deltaR = 2.0for coord in self.pos:if coord[0] > width + deltaR:coord[0] = - deltaRif coord[0] < - deltaR:coord[0] = width + deltaRif coord[1] > height + deltaR:coord[1] = - deltaRif coord[1] < - deltaR:coord[1] = height + deltaRdef applyRules(self):# apply rule #1: SeparationD = self.distMatrix < 25.0vel = self.pos*D.sum(axis=1).reshape(self.N, 1) - D.dot(self.pos)self.limit(vel, self.maxRuleVel)# distance threshold for alignment (different from separation)D = self.distMatrix < 50.0# apply rule #2: Alignmentvel2 = D.dot(self.vel)self.limit(vel2, self.maxRuleVel)vel += vel2;# apply rule #3: Cohesionvel3 = D.dot(self.pos) - self.posself.limit(vel3, self.maxRuleVel)vel += vel3return veldef buttonPress(self, event):"""event handler for matplotlib button presses"""# left-click to add a boidif event.button is 1:self.pos = np.concatenate((self.pos, np.array([[event.xdata, event.ydata]])), axis=0)# generate a random velocityangles = 2*math.pi*np.random.rand(1)v = np.array(list(zip(np.sin(angles), np.cos(angles))))self.vel = np.concatenate((self.vel, v), axis=0)self.N += 1# right-click to scatter boidselif event.button is 3:# add scattering velocityself.vel += 0.1*(self.pos - np.array([[event.xdata, event.ydata]]))def tick(frameNum, pts, beak, boids):boids.tick(frameNum, pts, beak)return pts, beakdef main():print('starting boids...')parser = argparse.ArgumentParser(description="Implementing CraigReynolds's Boids...")# add argumentsparser.add_argument('--num-boids', dest='N', required=False)args = parser.parse_args()# set the initial number of boidsN = 100if args.N:N = int(args.N)# create boidsboids = Boids(N)fig = plt.figure()ax = plt.axes(xlim=(0, width), ylim=(0, height))pts, = ax.plot([], [], markersize=10, c='k', marker='o', ls='None')beak, = ax.plot([], [], markersize=4, c='r', marker='o', ls='None')anim = animation.FuncAnimation(fig, tick, fargs=(pts, beak, boids),interval=50)# 用 mpl_connect()方法向 matplotlib 画布添加一个按钮按下事件cid = fig.canvas.mpl_connect('button_press_event', boids.buttonPress)plt.show()if __name__ == '__main__':main()
相关文章:

【Python 项目】类鸟群:仿真鸟群
类鸟群:仿真鸟群 仔细观察一群鸟或一群鱼,你会发现,虽然群体由个体生物组成,但该群体作为一个整体似乎有它自己的生命。鸟群中的鸟在移动、飞越和绕过障碍物时,彼此之间相互定位。受到打扰或惊吓时会破坏编队…...

基于信号处理的PPG信号滤波降噪方法(MATLAB)
光电容积脉搏波PPG信号结合相关算法可以用于人体生理参数检测,如血压、血氧饱和度等,但采集过程中极易受到噪声干扰,对于血压、血氧饱和度测量的准确性造成影响。随着当今社会医疗保健技术的发展,可穿戴监测设备对于PPG信号的质量…...

新一代信息技术及应用
关于云计算的描述不正确的是( )。 A 云计算可以通过网络连接,用户通过网络接入“云”中并获得有关的服务,“云”内节点之间也通过内部的网络相连 B 云计算可以快速、按需、弹性服务,用户可以按照实际需求迅速获取或释放…...

SVN 解决冲突
SVN 解决冲突 1. 引言 在软件开发过程中,版本控制是一个至关重要的环节。SVN(Subversion)作为一个流行的版本控制系统,被广泛应用于团队协作中。然而,当多个开发者同时对同一部分代码进行修改时,冲突是不可避免的。本文将详细介绍如何在SVN中解决这些冲突,以便团队成员…...

机器人前沿--PalmE:An Embodied Multimodal Language Model 具身多模态大(语言)模型
首先解释这篇工作名称Palm-E,发表时间为2023.03,其中的Palm是谷歌内部在2022.04开发的大语言模型,功能类似ChatGPT,只是由于各种原因没有那样火起来,E是Embodied的首字母,翻译过来就是具身多模态大语言模型…...

编程语言都是哪些人开发出来的?为什么都是国外较小国家的人
编程语言都是哪些人开发出来的? 编程语言的开发者通常是来自计算机科学、软件工程、数学、物理学等领域的专家、学者和工程师。这些开发者具备深厚的编程技能、算法知识、系统设计能力以及创新思维,他们致力于创造出能够解决特定问题或满足特定需求的编…...
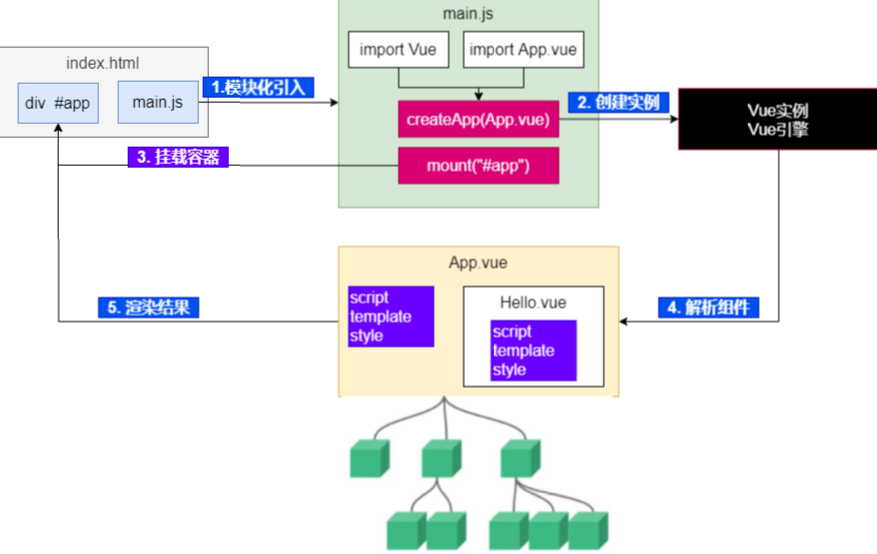
【前端速通系列|第二篇】Vue3前置知识
文章目录 1.前言2.包管理工具npm2.1下载node.js2.2配置 npm 镜像源2.3 npm 常用命令 3.Vite构建工具4.Vue3组件化5.Vue3运行原理 1.前言 本系列文章旨在帮助大家快速上手前端开发。 2.包管理工具npm npm 是 node.js中进行 包管理 的工具. 类似于Java中的Maven。 2.1下载nod…...
)
ES6 Module 的语法(十二)
ES6(ECMAScript 2015)引入了模块(Modules)的概念,使得JavaScript代码可以更容易地组织和复用。 1. export 关键字 命名导出 (Named Exports) 你可以使用 export 关键字导出多个变量、函数或类。 // module.js export…...

Redis 主从复制,哨兵与集群
目录 一.redis主从复制 1.redis 主从复制架构 2.主从复制特点 3.主从复制的基本原理 4.命令行配置 5.实现主从复制 6.删除主从复制 7.主从复制故障恢复 8.主从复制完整过程 9.主从同步优化配置 二.哨兵模式(Sentinel) 1.主要组件和概念 2.哨…...

CV05_深度学习模块之间的缝合教学(1)
1.1 在哪里缝 测试文件?() 训练文件?() 模型文件?(√) 1.2 骨干网络与模块缝合 以Vision Transformer为例,模型文件里有很多类,我们只在最后…...

【密码学】公钥密码的基本概念
在先前我写的密码学体制文章中谈到,现代密码学分为两大体制,介绍了一些有关对称密码体制诸如流密码和分组密码的内容。本文的主要内容则切换到公钥密码体制(又称非对称密码体制),简述了公钥密码体制的基本思想和应用方…...

【前端项目笔记】10 项目优化上线
项目优化上线 目标:优化Vue项目部署Vue项目(上线提供使用) 项目优化 项目优化策略: 生成打包报告:根据生成的报告发现问题并解决第三方库启用CDN:提高首屏页面的加载效率Element-UI组件按需加载路由懒加…...

Qt基础控件总结—多页面切换(QStackWidget类、QTabBar类和QTabWidget类)
QStackedWidget 类 QStackedWidget 类是在 QStackedLayout 之上构造的一个便利的部件,其使用方法与步骤和 QStackedLayout 是一样的。QStackedWidget 类的成员函数与 QStackedLayout 类也基本上是一致的,使用该类就和使用 QStackedLayout 一样。 使用该类可以参考QStackedL…...

团队融合与业务突破
结束了在上海久事集团下属公司的《团队融合与业务突破》课程,不仅探讨了团队领导力的关键技巧,更重要的是,我们从业务协同的视角,在跨团队中如何达成了共识,结合系统思考的相关内容,让大家看到跨部门冲突的…...

mybatilsplaus 常用注解
官网地址 baomidou注解配置...

vue引入sm-crypto通过sm4对文件进行加解密,用户输入密码
对文件加密并保存: import { sm4 } from sm-cryptofetch("你的文件地址") .then(response > response.blob()) .then(byteStream > {const reader2 new FileReader();reader2.onload function(event) {const arrayBuffer event.target.result;l…...

vue3实现无缝滚动列表(大屏数据轮播场景)
实现思路 vue3目前可以通过第三方组件来实现这个需求。 下面介绍一下这个第三方滚动组件--vue3-scroll-seamless vue3-scroll-seamless 是一个用于 Vue 3 的插件,用于实现无缝滚动的组件。它可以让内容在水平或垂直方向上无缝滚动,适用于展示轮播图、新…...

element ui ts table重置排序
#日常# 今天带的实习生,在遇到开发过程中,遇到了element ui table 每次查询的时候都需要重置排序方式,而且多个排序是由前端排序。 <el-table :data"tableData" ref"restTable"> </<el-table> <script…...

python热门面试题三
面试题1:Python中的列表推导式是什么?请给出一个例子。 回答: 列表推导式(List Comprehension)是Python中一种非常强大且简洁的构建列表的工具。它允许你通过一个表达式来创建一个新的列表,这个表达式定义…...

sql monitoring 长SQL ASH AWR 都没有 未Commit or export to csv
Duration 4小时, Database Time 22.5, Session Inactive, 1.未Commit原因, 2.慢慢导出成csv文件? How is v$session status INACTIVE and v$sql_monitor status EXECUTING concurrently 2641811 Posts: 8 Jan 11, 2016 6:47P…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
