【密码学基础】基于LWE（Learning with Errors）的全同态加密方案

学习资源：
全同态加密I：理论与基础（上海交通大学 郁昱老师）
全同态加密II：全同态加密的理论与构造（Xiang Xie老师）

---

现在第二代（如BGV和BFV）和第三代全同态加密方案都是基于LWE构造的，现在先进的全同态方案也都是基于LWE的，所以本文总结一下LWE的基础知识。
首先考虑，我们希望加密一个数$s$， 现在用一系列的$a_i$对$s$进行加密，得到$a_{i}s$，实际上通过求解最大公约数GCD就能求解出$s$。但是，如果加上一个随机噪声$e_i$，得到$a_{i}s+e_i$，那么将难以求解出$s$的值。这个过程就是我对LWE的简单理解，所谓error就是一个noise。

全同态加密的计算过程分为三步：密钥生成KeyGen、加密Enc、同态计算Eval、解密Dec。、

KeyGen：

首先构造出如上的等式，$s\cdot A+e=sA+e$，然后得到公钥pk（$-A$和$sA+e$的拼接），以及私钥sk（$s$和1的拼接）。于是得到pk和sk满足相乘后的结果是随机噪声e（接近0）。

Enc：

加密用的公钥pk，r是一个只包含0或1的随机向量，m是待加密的信息（放在向量的最低位上）。

Dec：

解密用的私钥sk，和ct计算完内积后求mod 2得到解密结果。

正确性证明：

sk和pk相乘得到2e（KeyGen时满足的条件），然后和r做内积得到一个很小的偶数噪声，最终的结果就是m+很小的偶数噪声，于是通过mod 2就能将噪声消除，得到解密结果m。这也就是为什么构造的噪声是2e，而不是e，我的理解就是希望通过构造偶数的随机噪声，从而在解密时方便用mod 2的方式消除掉噪声。

安全性证明：

当pk是伪随机的，r具有足够高的熵（也就是随机性很强？）时，pk和pk乘r都是伪随机的。自然和带m的向量相加后，加密结果也是伪随机的。

下面是Xiang Xie老师的公式化描述：
加密公式：密文c = 公钥pk ✖️ 随机r + 明文m
解密公式：明文m = <密文sk, 私钥sk> mod q mod 2

在这个基础上，再mod 2就能解密出明文m的值。只要噪声够小，就能保证正确性。
这里有个需要区分的事情：以上$PK=(A,b=A{s}^{\prime }+2e)$是BGV方案，BFV则是$PK=(A,b=A{s}^{\prime }+e)$，区别是BGV将信息编码在低位，而BFV将消息编码在高位（学习BFV的时候会说明）。

Eval（加法同态和乘法同态）：

注意到同态加法或乘法都会带来显著的噪声累积，并且乘法是呈平方增长趋势。
然后说说如何解密同态乘的结果，下面的式子可以看到：两个密文做乘法，等价于密文和私钥分别先做tensor product，然后再做内积。因此，显然密文和私钥的大小都翻了一倍。Example是一个等价性的证明。

那么问题来了，如何将同态乘之后的密文大小和私钥大小都恢复回去呢？这就是Key Switching解决的问题。

下面是Xiang Xie老师的描述：

Key Switching

目标是将密文和私钥的大小恢复到线性大小。

现在求密文c1和c2的乘法：

以上过程基于比特分解这个概念：

下面是Xiang Xie老师的描述：

Key Switching的目标：将私钥$\tilde{s}$下的$\tilde{c}$ 转换为 私钥$s$下的$c$，并且$\tilde{c}$和$c$都是加密的同一个明文。
这里有一个核心概念是Key Switching Key (KSK)，也就是用私钥$s$来加密$\tilde{s}$。

通过Key Switching过程，可以推导出私钥从$s\otimes s$变成了线性的$s$，同时密文从$\tilde{c}$变成了线性的$c$。并且通过最后一行式子可以看出，Key Switching后的$⟨c,s⟩$和原来的$⟨\tilde{c},s\otimes s⟩$之间相差了一个噪声$2{\tilde{c}}^T\tilde{e}$，这部分是可以非常大的！所以到这里仍然没办法实现Key Switching。

这里引入了一个Gadget矩阵G：

于是，Key Switching的过程变成了下面这样：

此时，增加的误差就非常小了。
总结一下就是，通过Key Switching，原来私钥$\tilde{s}=s\otimes s$下的$\tilde{c}=c\otimes c$，被转换成了私钥$s$下的$c$，注意Key Switching后的$s,c$都不是原来的值了（double check）。

对于BGV，加法的噪声线性增长，乘法的噪声平方增长，Key Switching虽然可以支持乘法了（限制sk变得特别大），但是实际上噪声是在原本乘法噪声基础上加了一个很小的噪声，总体也非常大。因此需要进一步降低这个噪声。

Modulus Reduction

到这里，通过LWE实现了很小深度的同态乘法和加法计算，key switching则是对每层用新的密钥，但是随着计算深度加深，噪声的扩大是爆炸性的，因此还不是一个levelled FHE（能计算指定深度的FHE）。
现在我们希望不借助bootstrapping，实现一个能计算一定深度的FHE，需要用到模数变换。

暂时没太看懂中间的流程，简而言之就是将密文c从模q的域变换到模p的域上（p<<q），于是噪声等比例缩小，也就是大约缩小到原来的p/q倍。
下面是一个具体的例子：
如果不做Modulus Reduction，随着深度加深，噪声呈双指数趋势增长，level >= 3之后就会带来解密错误。

如果每个level上做Modulus Reduction，那么噪声也会被维持在一个绝对值范围内，代价就是模数会不断减小。

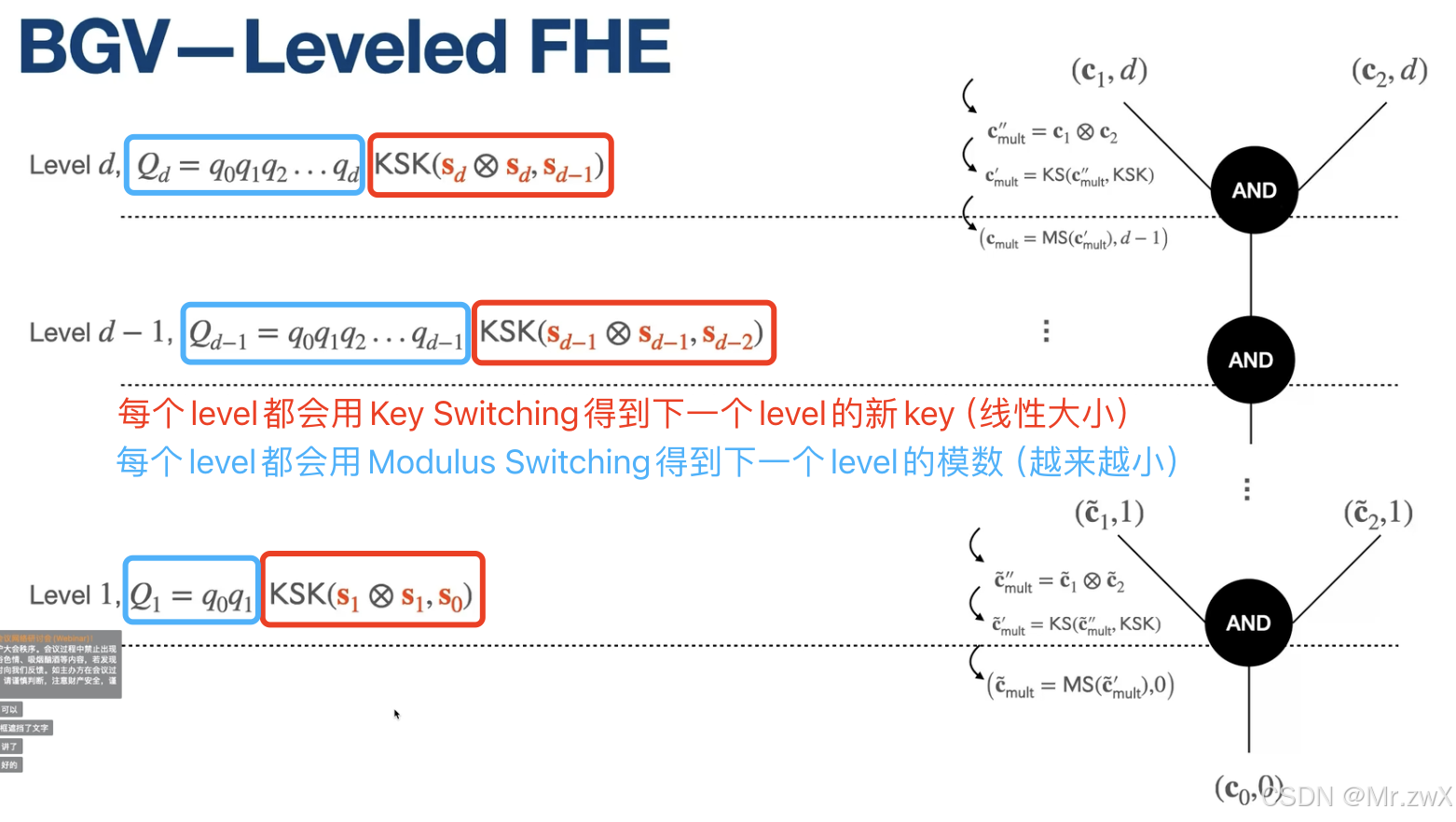
所以要想实现一个levelled FHE，可以设置一个模数$B^d$，然后就可以计算一个深度为$d$的电路了（其中$B$是刷新后密文的噪声上界）。计算完$d$的深度后，模数应该是降低到$B$，要保证此时解密不出错。BGV就是一种levelled FHE。