games103作业2（未完）

PBD方法

首先是每个质点的力的分析，不考虑碰撞和弹簧弹力的情况下，每个质点受重力的影响，所以需要对每个质点进行速度和位置的重力影响更新。

float 		t= 0.0333f;
float		damping= 0.99f;
int[] 		E;
float[] 	L;
Vector3[] 	V;
Vector3 gravity = new Vector3(0.0f, -9.8f, 0.0f);
......
for(int i=0; i<X.Length; i++)
{if(i==0 || i==20)	continue;V[i] = V[i] + gravity * t;V[i] *= damping;X[i] = X[i] + V[i] * t;//Initial Setup//...
}

思考一个问题，现实生活中布料的每个质点在拉扯变大以后，会越来越难以拉扯，基于胡可定律的弹簧模型中需要增大弹性系数k来模拟这种现象，但这会造成显式积分和隐式积分都出现问题，增大了模拟计算量。基于约束的方法被提出的动机就是想要解决这个问题。也就是PBD

使用Jacobi的方式对质点进行约束位置更新。然后通过PBD的算法流程对位置和速度进行更新。

	void Strain_Limiting(){Mesh mesh = GetComponent<MeshFilter> ().mesh;Vector3[] vertices = mesh.vertices;Vector3[] vertices_new = new Vector3[vertices.Length];int[] n = new int[vertices.Length];for(int i = 0; i < vertices.Length; i++){vertices_new[i] = new Vector3(0.0f, 0.0f, 0.0f);n[i] = 0;}for(int e = 0; e < L.Length; e++)//注意是消重的{int a = E[e * 2 + 0];int b = E[e * 2 + 1];Vector3 a_b = vertices[a] - vertices[b];float halfDistance = (a_b.magnitude - L[e])*0.5f;Vector3 pointMove = halfDistance * a_b.normalized;vertices_new[a] = vertices_new[a] + vertices[a] - pointMove;vertices_new[b] = vertices_new[b] + vertices[b] + pointMove;n[a]++;n[b]++;}for(int i = 0; i < vertices.Length; i++){if (i == 0 || i == 20) continue;V[i] = V[i] + ((vertices_new[i] + 0.2f * vertices[i]) / (n[i] + 0.2f) - vertices[i]) / t;vertices[i] = (vertices_new[i] + 0.2f * vertices[i]) / (n[i] + 0.2f);}//Apply PBD here.//...mesh.vertices = vertices;}

布料效果

球的撞击

在之前的课程中，求的是刚体对碰撞体进行撞击，所以最后要进行约束回来，但是这里不需要，这是流体。

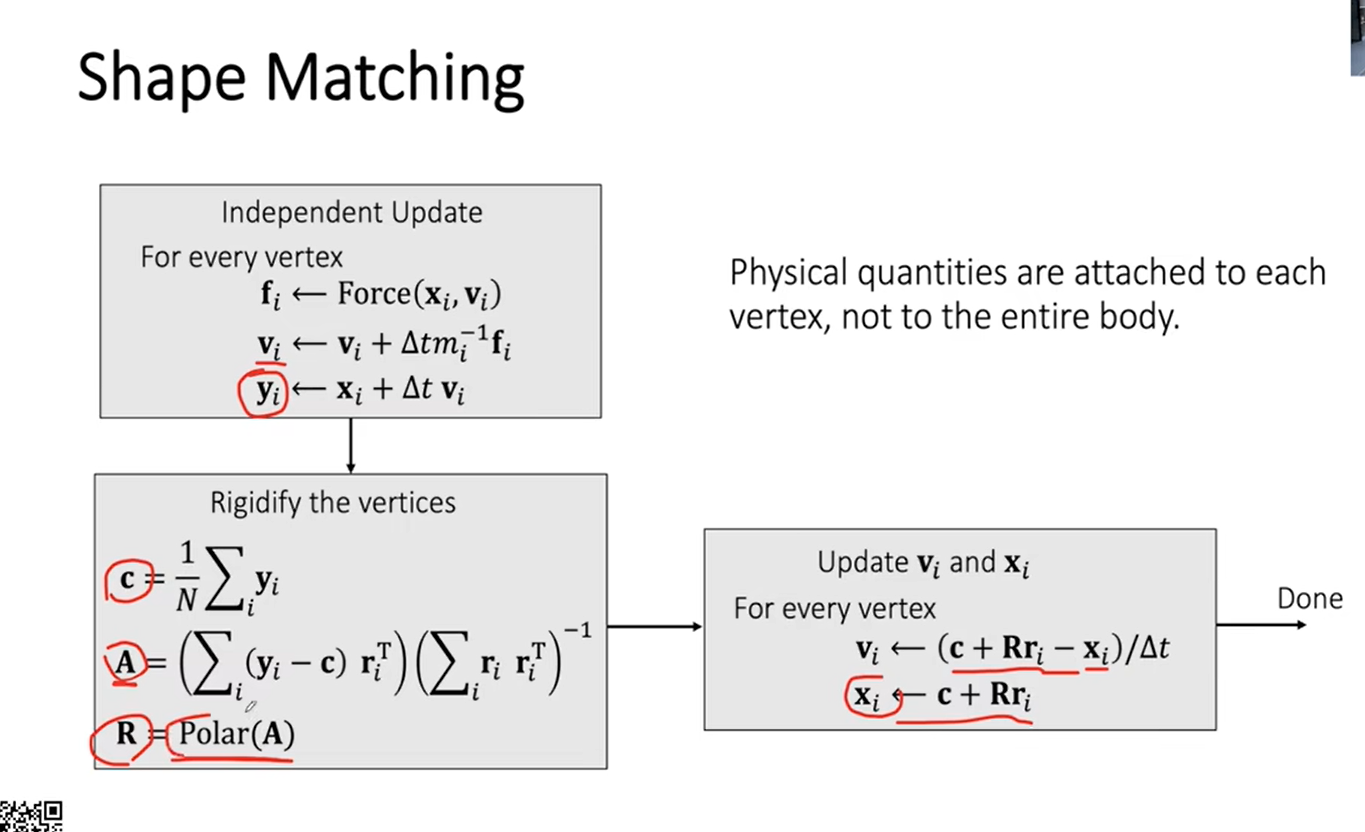
这里计算碰撞位移是在PBD以后，才计算是否发生碰撞以及碰撞后的速度和位移变换。（这些都算在一个帧内进行更新）

	void Collision_Handling(){Mesh mesh = GetComponent<MeshFilter> ().mesh;Vector3[] X = mesh.vertices;Vector3 spherePosition = sphere.transform.position;for(int i = 0; i < X.Length; i++){if (i == 0 || i == 20) continue;if ((X[i] - spherePosition).magnitude > r){continue;}//发生碰撞，得到碰撞点Vector3 collosionPoint = r * (X[i] - spherePosition).normalized + spherePosition;Vector3 normal = (collosionPoint - spherePosition).normalized;float jud = Vector3.Dot(V[i], normal);/*V[i] = V[i]+ (collosionPoint - X[i]) / t;X[i] = collosionPoint;*/Vector3 v_N = jud * normal;Vector3 v_T = V[i] - v_N;//作业这里的意思是碰撞以后，位移到球体表面v_N = v_N + (collosionPoint - X[i]) / t;X[i] = collosionPoint;V[i] = v_N + v_T;//忽略摩擦}//For every vertex, detect collision and apply impulse if needed.//...mesh.vertices = X;}

效果