贪心算法之区间问题总结
一、跳跃游戏
跳跃游戏类的问题,不关心每一步怎么跳,只需要关心最大覆盖范围
这里注意i是在当前最大可覆盖范围内遍历,如{2,1,0,1},就是在0~2范围内遍历,千万不能0~numsSize-1范围内遍历!!!
bool canJump(int* nums, int numsSize){//不关心每一步怎么跳,只需要关心最大覆盖范围int cover=0;for(int i=0;i<=cover;i++){cover=fmax(cover,nums[i]);if(cover>=numsSize-1) return true;}return false;
}二、跳跃游戏II
没见过不好想,建议记下来
关键是当前覆盖范围和下一步覆盖范围都要考虑
计算下一步覆盖范围的目的是用来更新当前覆盖范围,以保证跳跃步数最少
int jump(int* nums, int numsSize){//统计两个覆盖范围:当前这一步的最大覆盖和下一步最大覆盖//如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,//那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点if(numsSize==1) return 0;int curCover=0,nextCover=0;int result=0;for(int i=0;i<=curCover;i++){nextCover=fmax(nextCover,i+nums[i]);if(i==curCover){if(curCover<numsSize-1){result++;curCover=nextCover;if(nextCover>=numsSize-1) break;}else break;}}return result;
}三、无重叠区间
区间重叠类问题第一步:排序
区间判断重叠方法:若当前区间的右边界大于下一个区间的左边界,则表示有重叠
合并实质上就是更新当前区间的右边界
class Solution {
private:static bool cmp(const vector<int> &a,const vector<int> &b){return a[0]<b[0];}
public:int eraseOverlapIntervals(vector<vector<int>>& intervals) {//按照区间左边界从小到大排序//若当前区间的右边界大于下一个区间的左边界,则表示有重叠//可以把移除理解成一种特殊的合并,所有重叠区间合并之后,右边界为最小的那个if(intervals.size()==1) return 0;sort(intervals.begin(),intervals.end(),cmp);int result=0;for(int i=1;i<intervals.size();i++){if(intervals[i-1][1]>intervals[i][0]){intervals[i][1]=fmin(intervals[i-1][1],intervals[i][1]);result++;}}return result;}
};四、用最少数量的箭引爆气球
实际上这题就是在问:有多少组无重叠区间,和上题都在研究重叠与无重叠区间的问题
注意本题的重叠区间内的所有区间的右边界和上题一样,也要更新为重叠区间里最小的右边界
因为找最大重叠个数的重叠区间看的是“短板”!!!
class Solution {
private:static bool cmp(const vector<int> &a,const vector<int> &b){return a[0]<b[0];}
public:int findMinArrowShots(vector<vector<int>>& points) {if(points.size()==1) return 1;sort(points.begin(),points.end(),cmp);int result=1;for(int i=1;i<points.size();i++){if(points[i-1][1]<pointss[i][0])result++;elsepoints[i][1]=min(points[i-1][1],points[i][1]);}return result;}
};五、划分字母区间
本题实际上就是在问:求每个闭包的长度
所以关键就是,怎么判断闭包的起始位置
这就和跳跃游戏II有点像了~
class Solution {
public:vector<int> partitionLabels(string s) {//开辟一个数组记录每个字母的最后出现位置int cover[27];for(int i=0;i<s.size();i++)cover[s[i]-'a']=i;//到达最大覆盖距离时(可以理解成这个闭包的最大覆盖范围),//记录该覆盖范围的长度,然后向后移动一个位置int left=0,right=0;vector<int> result;for(int i=0;i<s.size();i++){right=max(right,cover[s[i]-'a']);if(i==right){result.push_back(right-left+1);left=i+1;}}return result;}
};六、合并区间
所谓合并区间,其实就是重叠区间的右边界取重叠区间内最大右边界
如果下一个区间和当前重叠区间重叠,则更新当前重叠区间的右边界;
若不重叠,说明是新的闭包,上一个重叠区间更新完成,插入result新的重叠区间
class Solution {
private:static bool cmp(const vector<int> &a,const vector<int> &b){return a[0]<b[0];}
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {//所谓合并区间,其实就是重叠区间的右边界取重叠区间内最大右边界//如果下一个区间和当前重叠区间重叠,则更新当前重叠区间的右边界;//若不重叠,说明是新的闭包,上一个重叠区间更新完成,插入result新的重叠区间if(intervals.size()==1) return intervals;sort(intervals.begin(),intervals.end(),cmp);vector<vector<int>> result;result.push_back(intervals[0]);for(int i=1;i<intervals.size();i++){if(intervals[i-1][1]>=intervals[i][0])result.back()[1]=max(intervals[i][1],result.back()[1]);elseresult.push_back(intervals[i]);}return result;}
};相关文章:

贪心算法之区间问题总结
一、跳跃游戏跳跃游戏类的问题,不关心每一步怎么跳,只需要关心最大覆盖范围这里注意i是在当前最大可覆盖范围内遍历,如{2,1,0,1},就是在0~2范围内遍历,千万不能0~numsSize-1范围内遍历!!&#x…...
无线WiFi安全渗透与攻防(七)之WIFI07-WEP-wifite自动化渗透WEP加密
WIFI07-WEP-wifite自动化渗透WEP加密 1.wifite介绍 wifite是一款自动化wep、wpa以及wps破解工具,不支持windows和osx。wifite的特点是可以同时攻击多个采用wep和wpa加密的网络。wifite只需简单的配置即可自动化运行,期间无需人工干预。 目前支持任何li…...
震撼,支持多模态模型的ChatGPT 4.0发布了
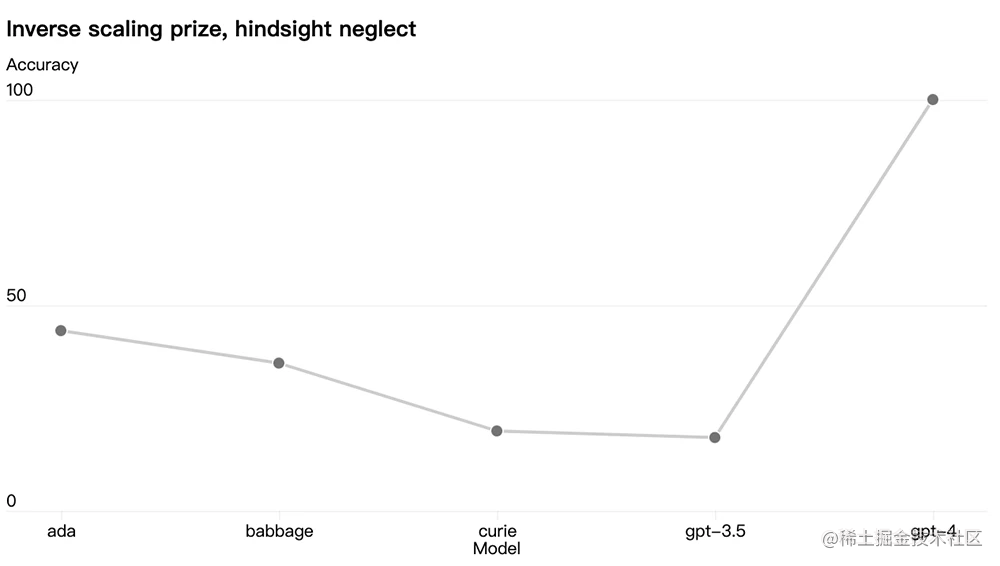
最近几个月,互联网和科技圈几乎ChatGPT刷屏了,各种关于ChatGPT的概念和应用的帖子也是围绕在周围。当去年年底ChatGPT发布的那几天,ChatGPT确实震撼到了所有人,原来AI还可以这么玩,并且对国内的那些所谓的人工智能公司…...
IDEA常用插件列表
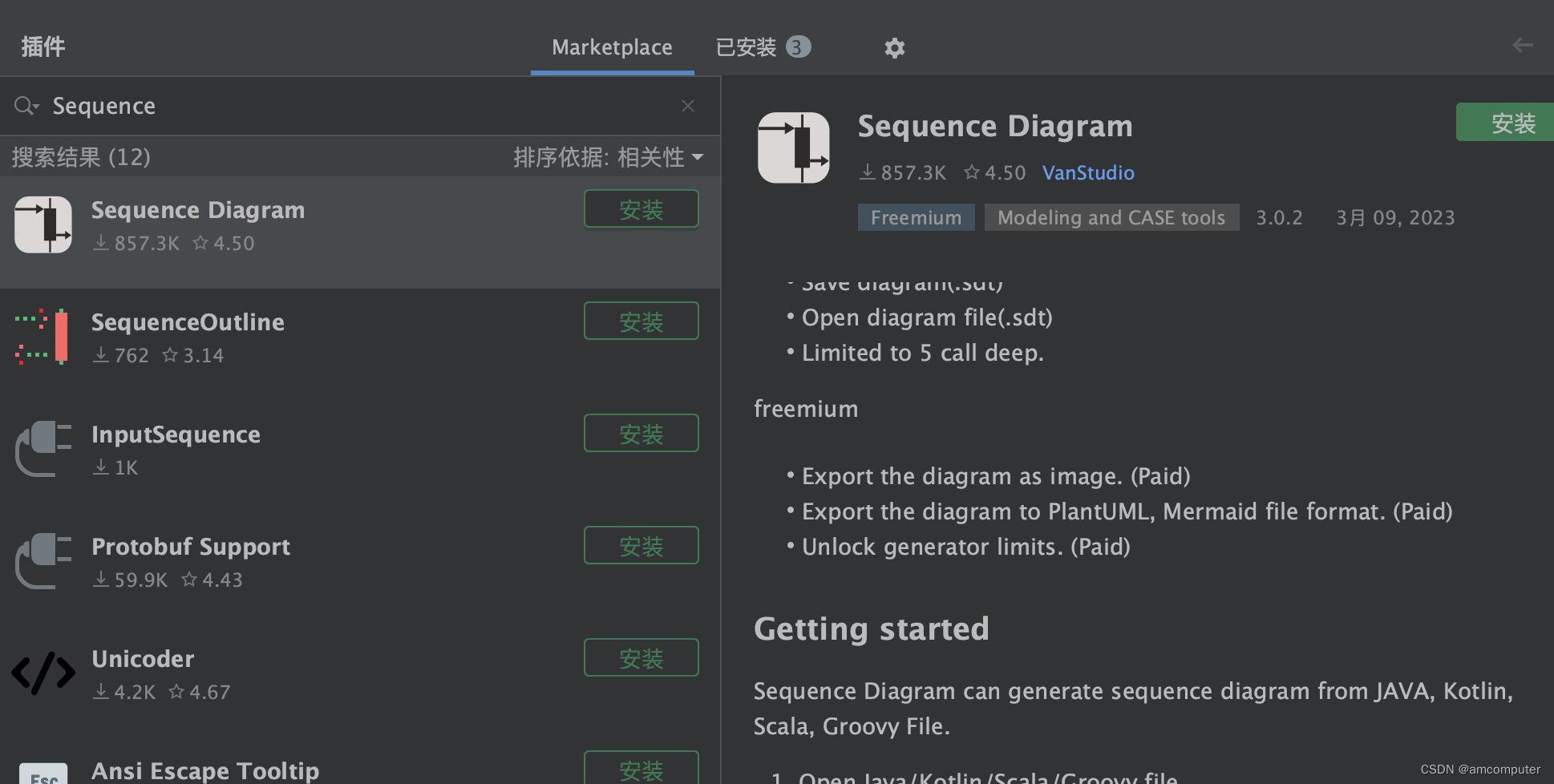
一 背景 IDEA常用插件列表,用来提供工作效率。你都安装了吗 IntelliJ IDEA 默认安装并提供了非常多的工具,比如 Maven Integration、Markdown support、SSH Remote Run 等。其中有很多好用,但是不为人知的工具。 二 插件列表 阿里代码规约…...

比df更好用的命令!
大家好,我是良许。 对于分析磁盘使用情况,有两个非常好用的命令:du 和 df 。简单来说,这两个命令的作用是这样的: du 命令:它是英文单词 disk usage 的简写,主要用于查看文件与目录占用多少磁…...
【Git使用学习】记录学习过程(1)
安装就省略了,安装结果如下。 Git Bash:这是一个模拟Linux环境的命令行工具,可以使用Git的所有功能。Git GUI:这是一个图形化界面的工具,可以方便地执行Git的常用操作。Git CMD:这是一个Windows命令行工具&…...
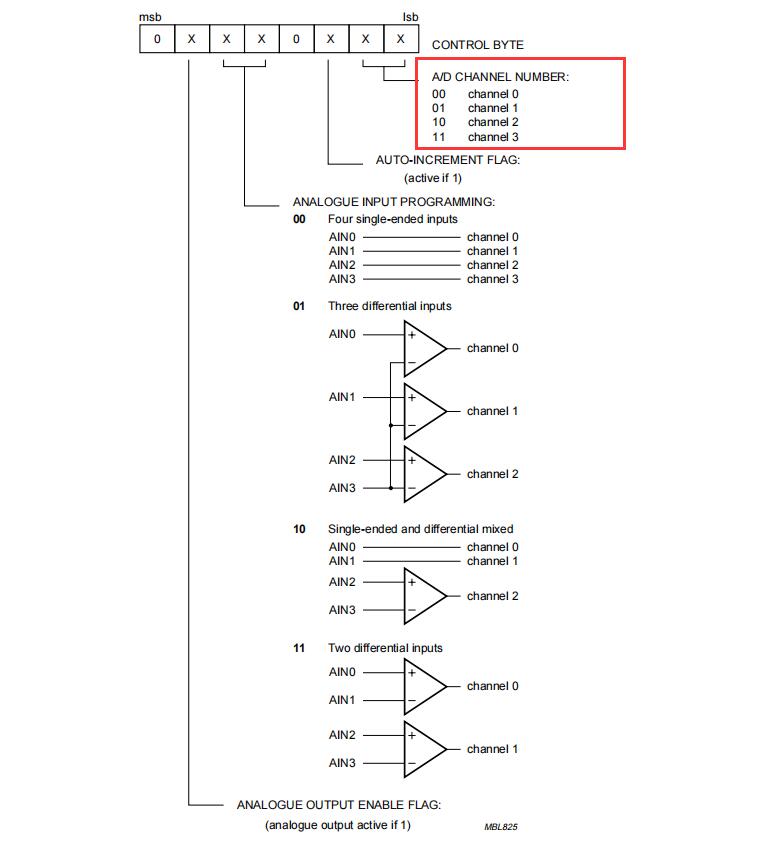
K_A18_001 基于STM32等单片机采集MQ2传感参数串口与OLED0.96双显示
K_A18_001 基于STM32等单片机采集MQ2传感参数串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:四、部分代码说明1、接线引脚定义1.1、STC89C52RCMQ2传感参模块1.2、STM32F103C8T6MQ2传感参模块五、基础知识学习与相关…...

【云原生·Docker】常用命令
目录 🍁1、管理命令 🍁2、帮助命令 🍁3、镜像命令 🍁4、容器命令 🍂4.1.查看容器 🍂4.2.创建容器 🍂4.3.删除容器 🍂4.4.拷贝文件 🍂4.5.查看容器IP 🍁5、部署…...

户外露营储能电源芯片CSU3AF10
户外露营的项目有很多,随着户外储能电源的发展,越来越多的电子产品可以在户外使用,也不用担心因为在户外时间过长而手机或者其他电子产品电量耗尽。户外储能电源可保证人们随时随地的用电需求,同时也可以满足家电炊具的供电需求&a…...

无线WiFi安全渗透与攻防(八)之WEP-Hirte渗透WEP加密
WEP-渗透WEP新思路–Hirte 1.Hirte介绍 Hirte是破解无线网络WEP Key的一种攻击类型 只要客户端设备(笔记本电脑,手机等)连接过的无线网络,那些WIFI即使是不在攻击者范围内也都能被破解,因为该wifi的WEP密钥和配置文…...

前端常考面试题整理
display:none与visibility:hidden的区别 这两个属性都是让元素隐藏,不可见。两者区别如下: (1)在渲染树中 display:none会让元素完全从渲染树中消失,渲染时不会占据任何空间;visibility:hidden不会让元素…...
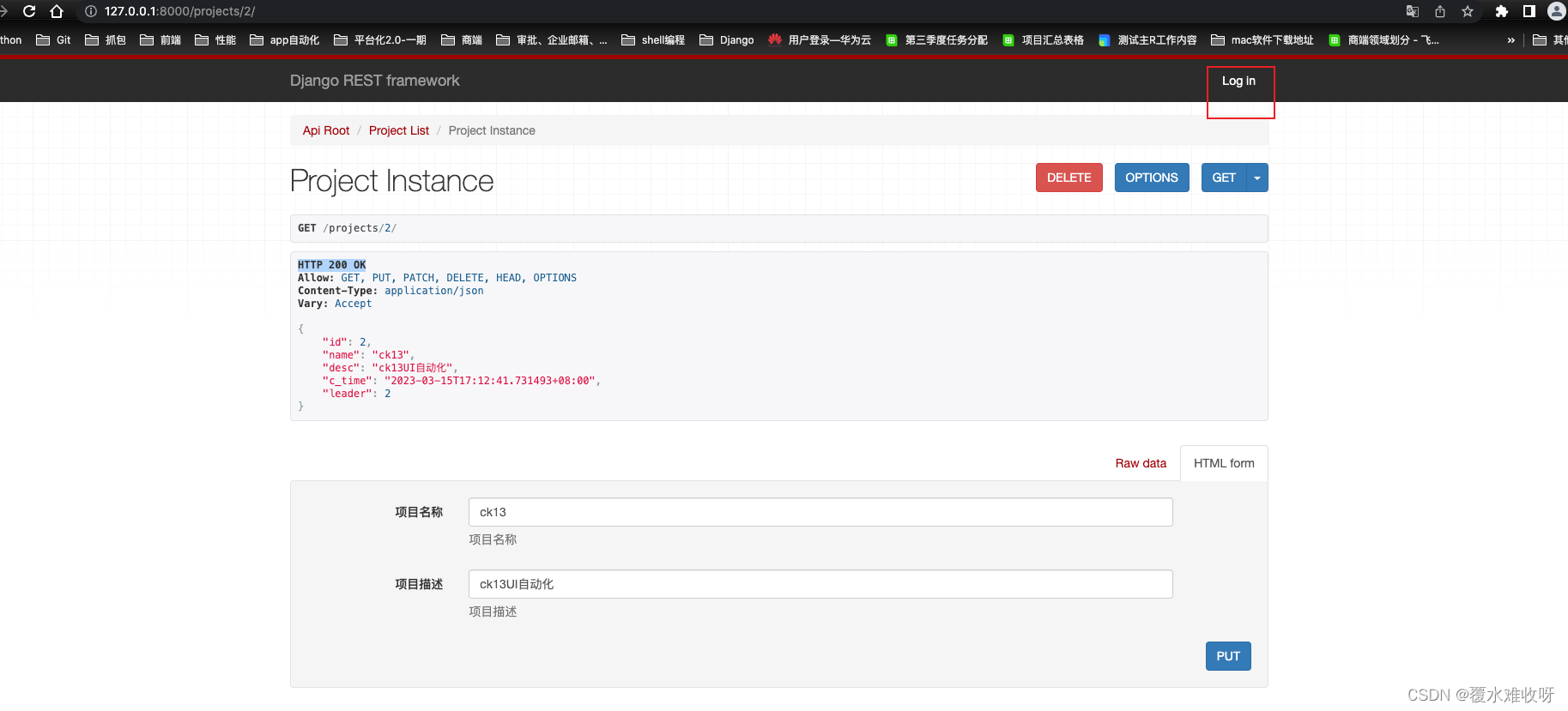
二十二、身份验证与权限
一、 准备工作 为了讲清楚身份验证与权限,我们再创建一个应用projects,设计模型如下: class Project(models.Model):name models.CharField(项目名称, max_length20, help_text项目名称)desc models.CharField(项目描述, max_length200, help_text项目…...
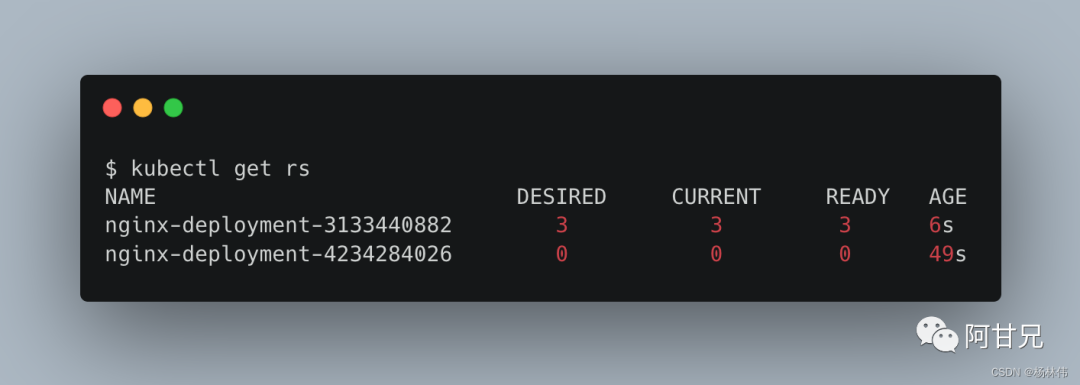
k8s pod 升级与回滚
当集群中的某个服务需要升级时,我们需要停止目前与该服务相关的所有pod,然后下载新版本镜像并创建新的pod。如果集群规模比较大,则这个工作变成了一个挑战,而且先全部停止然后逐步升级的方式会导致较长时间的服务不可用。kubernet…...
【Go】Go语言开发环境安装
【Go】Go语言开发环境安装 导入 安装环境:Winowds 我现在是win7安装的,与win10整体步骤是一样的,只是部分显示的时候有点差异不影响; 【名词】 编译器:先将代码编译成可执行文件,再执行; —…...

el-switch使用
效果图: 1.表格代码,给el-waitch加上change事件 <el-table-column prop"status" label"状态" align"center" width"150"> <template slot-sc…...

【算法入门】字符串基础
目录 一.字符串引言1.字符串基础二.洛谷P5734详解1.字符串相关库函数💫(1) strcpy函数 💫💫(2) strcat函数 💫💫(3)strstr函数 💫2.题…...
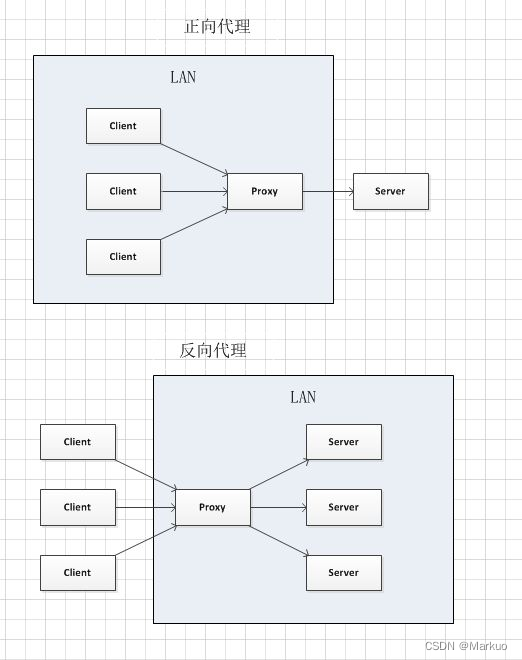
前端面试题 —— 浏览器原理(二)
目录 一、有哪些可能引起前端安全的问题? 二、网络劫持有哪几种,如何防范? 三、浏览器渲染进程的线程有哪些 四、僵尸进程和孤儿进程是什么? 五、为什么需要浏览器缓存? 六、对浏览器的理解 七、CSS 如何阻塞文档解析&…...

对于植物神经紊乱的治疗 中医采用辩证论治的方法
植物神经紊乱是由于心理压力过大、长期生活不规律所导致的一种疾病,这种疾病的发生往往是症状多样、涉及广泛的。当患有植物神经紊乱之后,主要的症状会以躯体化障碍为常见症状,但是很多患者还会出现情绪失控、睡眠障碍等问题。 对于植物神经紊…...

chatGPT之Python API启用上下文管理
chatGPT已经爆火一段时间了,我想大多数的开发者都在默默的在开发和测试当中,可能也是因为这个原因所以现在很难找到关于开发中遇到的一些坑或者方法和技巧。为什么别人的机器人能联想之前的语料,而你的却像个每次都只如初见的高冷机器人&…...
油田钻井实时在线监测系统
油田钻井的井下油层的压力不断变化,环境深度和压力巨大,且井下原油具有一定的流动性,实时在线压力监测是石油开采行业的难点。为更好地了解油田开采过程中油层的状况,提高油田开采效率和产量,油田钻井实时在线监测系统…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
