【Python实战因果推断】35_双重差分6

目录

Strict Exogeneity

No Time Varying Confounders

No Feedback

No Carryover and No Lagged Dependent Variable

---

Strict Exogeneity

严格的外生性假设是一个相当技术性的假设，通常用固定效应模型的残差来表示：

严格的异质性说明：

这一假设更为有力，意味着平行趋势。它也相当晦涩难懂，因此我认为我们最好从它的含义来讨论它：
1. 没有随时间变化的混杂因素
2. 无反馈
3. 无结转效应
您还可以通过 DAG 展示这一假设，使其更加直观：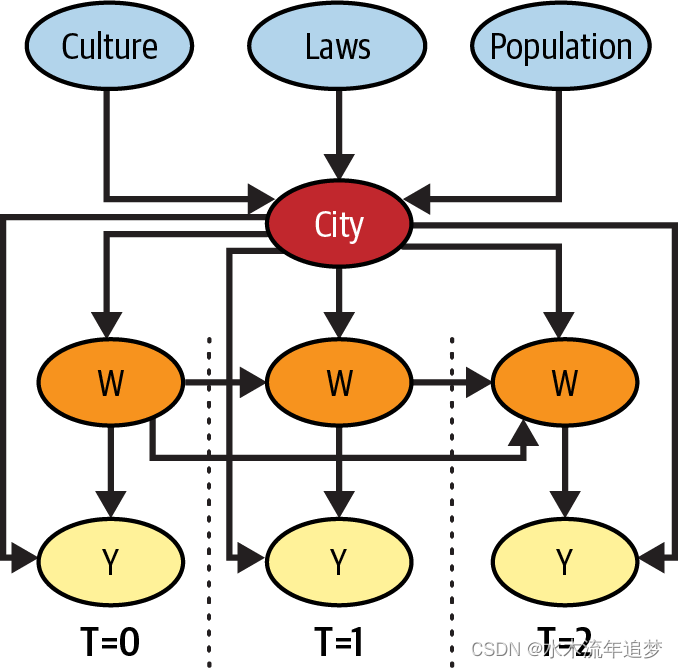

现在，让我们来看看它的真正含义

No Time Varying Confounders

首先告诉大家一个好消息。还记得我提到过面板数据可以利用时间和单位相关性吗？值得注意的是，即使存在未观察到的混杂因素，随着时间的推移重复观察也能帮助你识别因果效应。只要这些混杂因素在一段时间内或在所有单位中都是不变的，就可以做到这一点。为了更好地理解这一点，我们再来看看市场营销的例子。每个城市都有其独特的文化、法律和人口，所有这些都会对干预变量和结果变量产生重大影响。其中一些变量（如文化和法律）很难量化，因此成为您需要考虑的未观察混杂因素。然而，在无法测量这些变量的情况下，如何才能做到这一点呢？

诀窍在于，通过放大一个单位并跟踪其如何随时间演变，您已经控制了任何随时间固定的因素。这包括任何时间固定的混杂因素，甚至是那些无法测量的因素。在市场营销的例子中，如果某个城市的下载量随着时间的推移而增加，你就知道这不可能是由于城市文化的变化造成的（至少不是在短时间内），原因很简单，因为混杂因素是随时间固定的。底线是，即使你无法控制时间固定的混杂因素，因为你无法测量它，但如果你控制了单位本身，你仍然可以阻止通过它的后门路径。

如果你比较擅长数学，你也可以看到数据去势的过程是如何抹去任何时间固定的协变量的。回想一下，添加单位固定效应可以通过添加单位虚拟变量来实现，也可以通过按单位计算干预和结果的平均值，然后从原始变量中减去：

这里，我用 来表示干预，因为 Di 是时间固定的。在去中心化后，任何未观测到的 Ui 都会消失。由于 Ui 在不同时间是不变的，所以 ，这使得 无处不在。通俗地说，单位固定效应抹去了任何跨时间不变的变量。

我的重点是单位固定效应，但类似的论证也可以用来说明时间固定效应如何抹去任何在单位间固定但在时间上变化的变量。在我们的例子中，这些变量可能是国家的汇率或通货膨胀。由于这些都是全国性变量，因此对所有城市来说都是一样的。

当然，如果未观察到的混杂因素随时间和单位而变化，那就没办法了。

No Feedback

你可能已经注意到，前面的图表中还有一个重要的假设。具体来说，没有从过去的干预结果 向当前的治疗结果 延伸的箭头。换句话说，没有反馈。这意味着不能根据干预结果轨迹来决定治疗方法。为了说明这一点，假设干预是一个以时间 为索引的向量。在这种情况下，必须一次性决定整个向量。这在你之前看到的那种分块设计中是可行的，在这种设计中，干预在某一特定时间段开始，并无限期地持续下去。然而，即便如此，无反馈假设也可能被违反。例如，假设营销团队决定，只要某个城市的下载量达到 1000 次，他们就会开展线下营销活动。这就违反了无反馈假设。

No Carryover and No Lagged Dependent Variable

除了没有反馈之外，您可能还会注意到，由于没有从过去的干预结果到当前结果的箭头，因此该图也假定没有结转效应。幸运的是，如果扩展模型，包括干预的滞后版本，就可以放宽这一假设。例如，如果您认为第 t - 1 期的干预会影响第 t 期的结果，您可以使用下面的模型：

最后，该图还假设没有滞后因变量，这意味着过去的结果不会直接导致当前的结果。幸运的是，这个假设其实并不必要；从过去的 Y 到未来的 Y 添加箭头并不会妨碍识别。