Java【归并排序】算法, 大白话式图文解析(附代码)
文章目录
- 前言
- 一、排序相关概念
- 1, 什么是排序
- 2, 什么是排序的稳定性
- 3, 七大排序分类
- 二、归并排序
- 1, 图文解析
- 2, 代码实现
- 三、性能分析
- 四、七大排序算法总体分析
前言
各位读者好, 我是小陈, 这是我的个人主页
小陈还在持续努力学习编程, 努力通过博客输出所学知识
如果本篇对你有帮助, 烦请点赞关注支持一波, 感激不尽
希望我的专栏能够帮助到你:
JavaSE基础: 从数据类型 到 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等
Java数据结构: 顺序表, 链表, 二叉树, 堆, 哈希表等 (正在持续更新)
JavaEE初阶: 多线程, 网络编程, html, css, js, severlet, http协议, linux等(正在持续更新)
本篇继续分享七大排序算法中的 希尔排序 , 其余六个算法也有介绍噢
想看哪个点哪个 : 直接插入排序, 选择排序, 希尔排序, 堆排序, 冒泡排序, 快速排序
提示:是正在努力进步的小菜鸟一只,如有大佬发现文章欠佳之处欢迎评论区指点~ 废话不多说,直接发车~
一、排序相关概念
1, 什么是排序
📌排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增📈或递减📉的排列起来的操作
👉以 int 类型数据从小到大排序为例:
排序前:4,1,3,6,8,7,2,5
排序后:1,2,3,4,5,6,7,8
2, 什么是排序的稳定性
📌稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
👉以 int 类型数据从小到大排序为例:
排序前:4,1,3a,6,8,7,2,3b,5(3a 在 3b 之前)
排序后:1,2,3a,3b,4,5,6,7,8(3a 还在 3b 之前,稳定)
排序后:1,2,3b,3a,4,5,6,7,8(3a 不在 3b 之前,不稳定)
3, 七大排序分类
以下是常见的 7大排序 算法
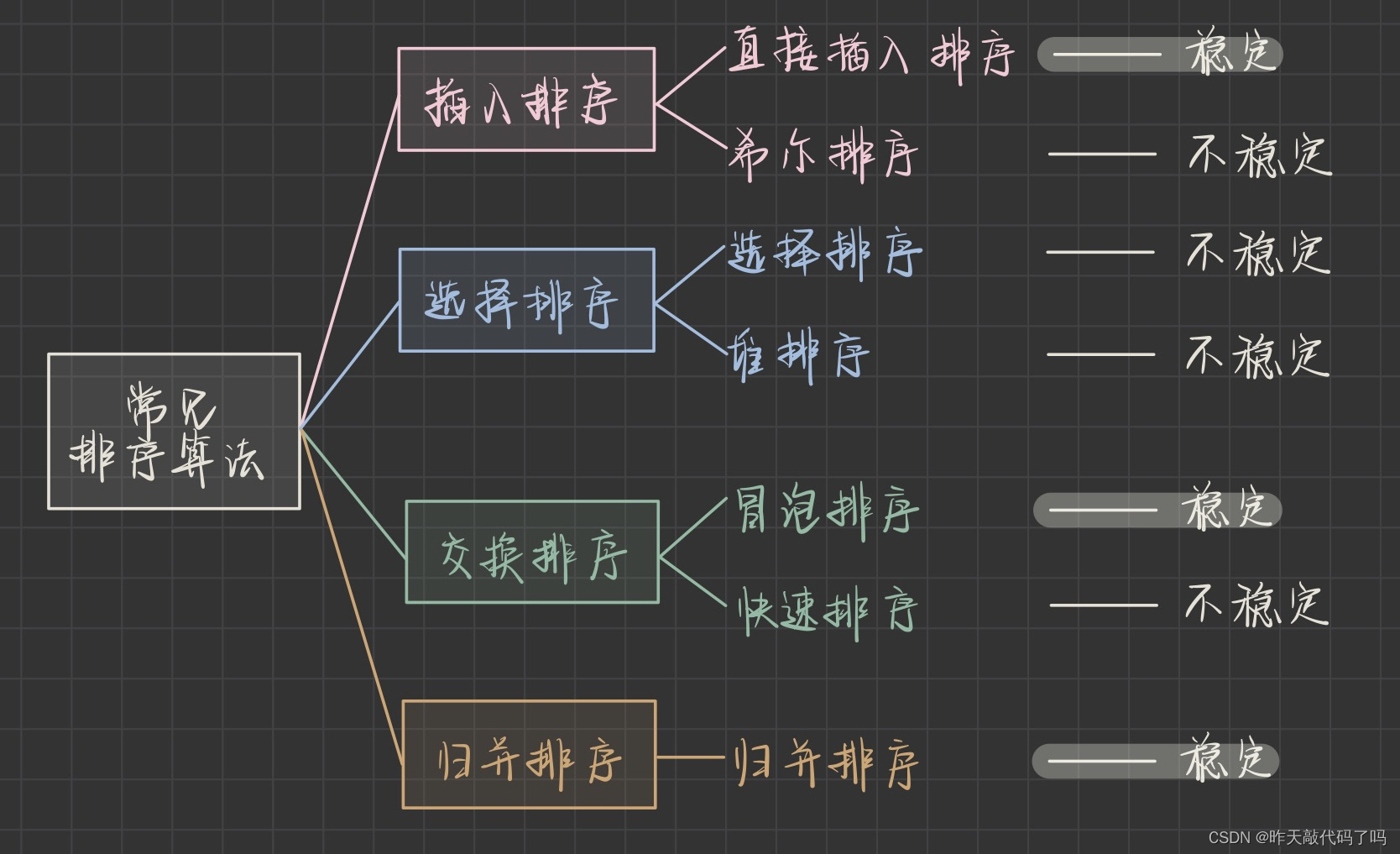
二、归并排序
1, 图文解析
📌归并排序 是建立在归并操作上的一种有效的排序算法, 该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
📌基本思想:假如一个学校只有两个班,怎么算出全校成绩排名呢,一般是先在各自班里排好序,然后两个班再一起排序,在两个班的成绩表各自有序的情况下,合并起来排序肯定要比整体混乱着排序效率高
假如一个班1000个人,那在班内排名也是相对效率低的,那咋办?可以再把每个班分成若干个小组先排,再合并几个小组整体排序,这不就是递归吗
归并归并,我的理解就是,递归分割原始数组,分割到足够小时,递归结束,然后返回时合并,并且完成排序
过程图解:

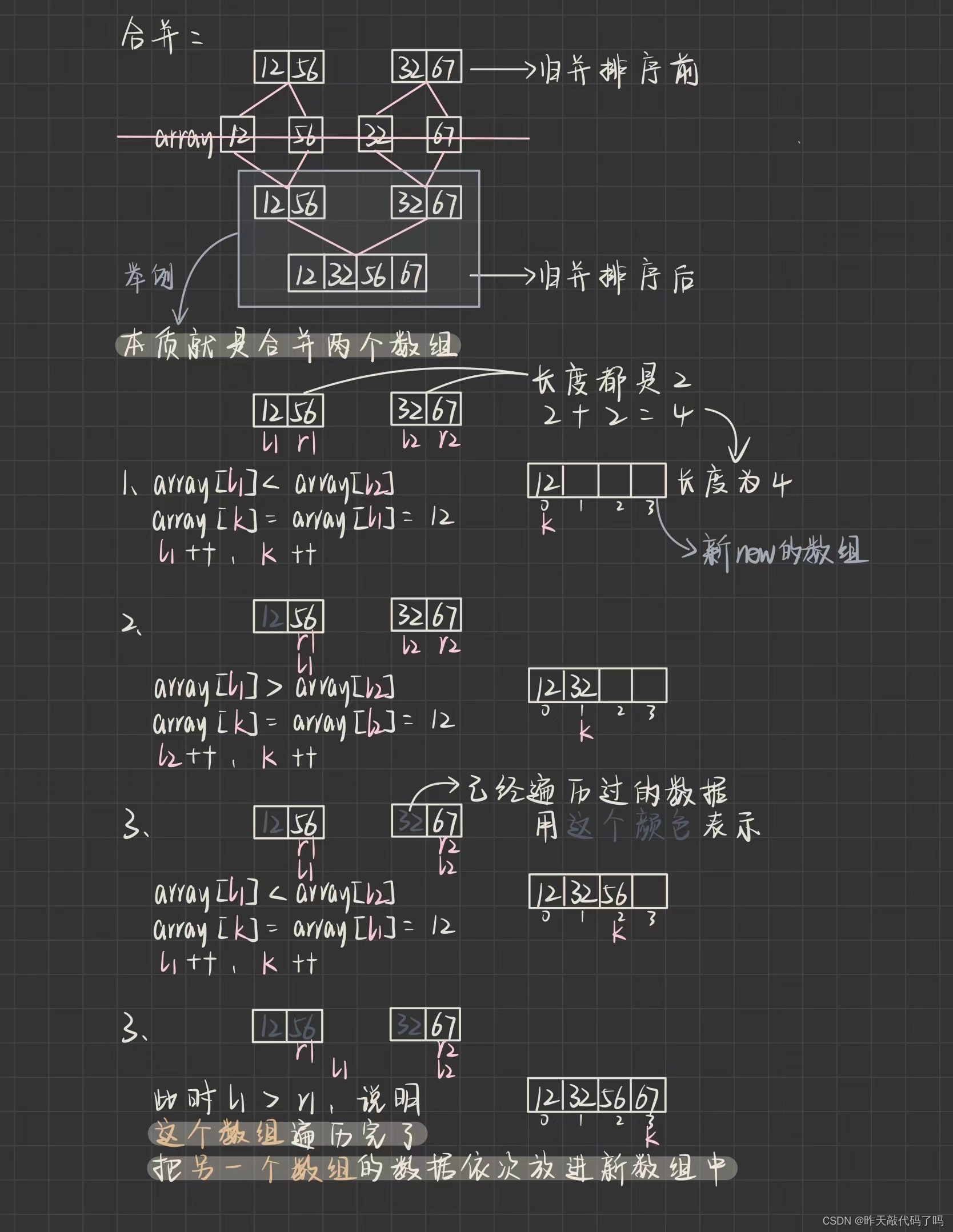
⚠️⚠️需要重点理解的是:
❗️❗️在递归进行分割的过程中,没有在物理上真正把数组切开(new了新的数组空间)的,只是函数的参数列表中有数组,left 和 right 下标,只是改变了 left 和 right 的值
❗️❗️但是在归并的过程中,才是真正的把两个数组的数据合起来(new了新的数组空间),然后再遍历挨个拷贝回原始数组中的。
2, 代码实现
体现封装的思想:把分割和合并两个方法独立封装起来,并设置成private
/*** 归并排序* 时间复杂度:O(N^logN)* 空间复杂度:O(N)* 稳定性:稳定* @param array*/public static void mergeSort(int[] array) {divid(array, 0, array.length - 1);}private static void divid(int[] array, int left, int right) {if (left >= right) {return;}int mid = (left + right) >>> 1;divid(array, left, mid);divid(array, mid + 1, right);merge(array, left, right, mid);}private static void merge(int[] array, int left, int right, int mid) {// 其实就是合并两个数组,并使合并后的数组有序int l1 = left;int l2 = mid + 1;int[] tmp = new int[right - left + 1];int i = 0;while(l1 <= mid && l2 <= right) {// 为什么要加等号,防止死循环if(array[l1] <= array[l2]) {tmp[i++] = array[l1++];}if (array[l2] <= array[l1]) {tmp[i++] = array[l2++];}}// 判断哪个数组还有数据while(l1 <= mid) {tmp[i++] = array[l1++];}while(l2 <= right) {tmp[i++] = array[l2++];}for (int j = 0; j < tmp.length; j++) {array[j + left] = tmp[j];}}
⚠️⚠️
注意最后一个 for 循环,这段代码作用是把合并好的有序子数组挨个拷贝回原始数组,但是 array[ j + left ] = tmp[j] 如何理解❓
因为你左右树都递归进行分割合并啊!如果原本在原始数组右边的子数组排有序之后, 应该从原数组的对应位置依次拷贝子数组
如果没有 j + left 这个操作, 就相当于每次都从原数组的 0 下标开始拷贝子数组
三、性能分析
👉时间复杂度::
和快速排序类似,也是递归次数+每次的 i,j 遍历时间,最好最坏平均情况的时间复杂度都是O(N*log₂N)
👉空间复杂度::
递归的开销是O(log₂N),但是需要总长度为N的额外数组空间的消耗,所有总体空间复杂度是O(N+log₂N)
👉稳定性::
稳定
只要是交换时, 两数据相邻就是稳定的算法,只要是跳跃式的交换就是不稳定, 当然别忘了, 稳定的算法也可以修改代码更改成不稳定的
四、七大排序算法总体分析
建议对七大算法都有认识之后, 再对比分析~~
想看哪个点哪个 : 直接插入排序, 选择排序, 希尔排序, 堆排序, 冒泡排序, 快速排序
没有完美的排序算法,任何一种算法都是有优点和缺陷的,即便是大名鼎鼎的快速排序,也只是整体上效率比较高,性能相对更优越
现在就整体分析一下各种排序的优缺点📊
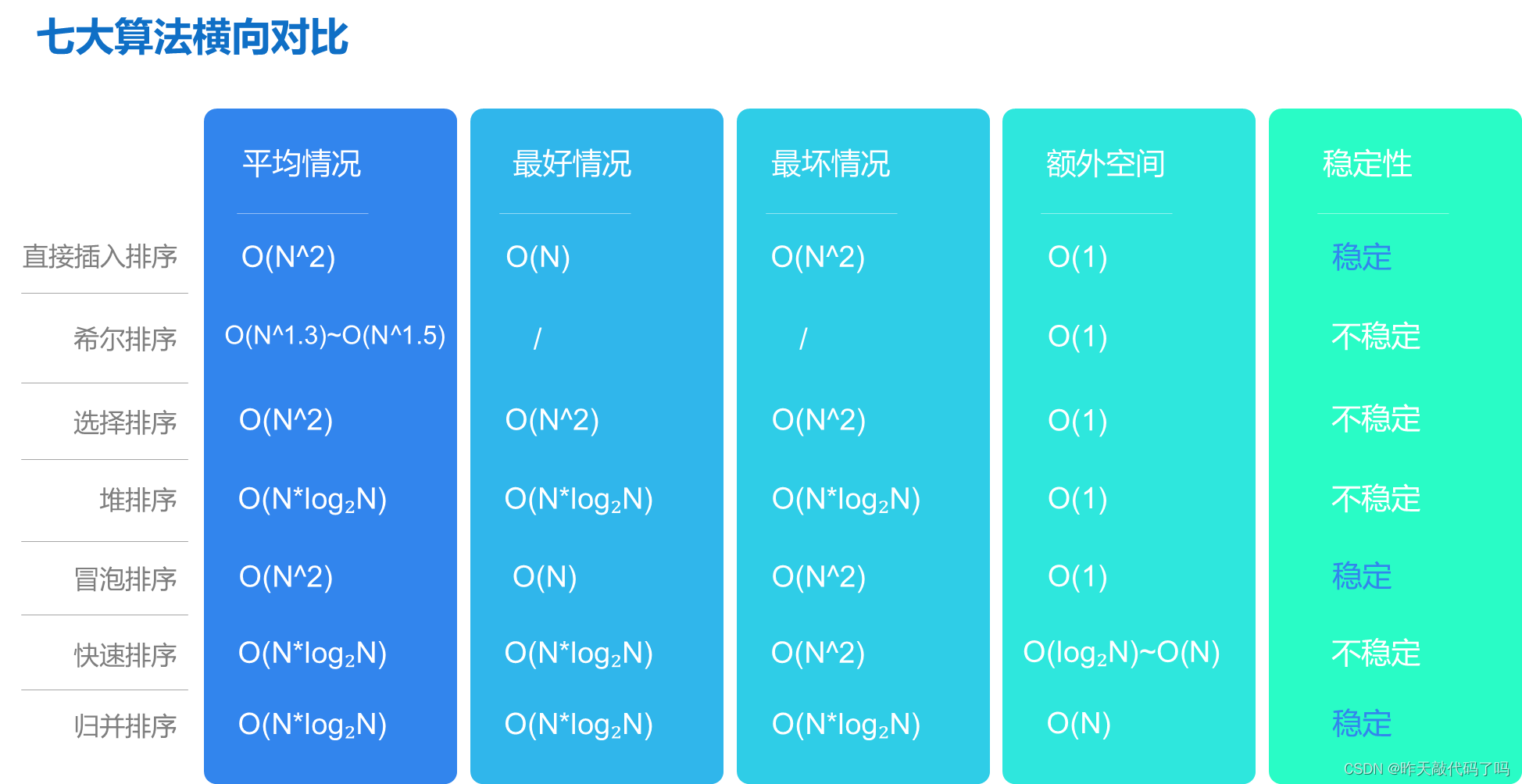
早期的排序算法平均时间复杂度都是O(N^2); 因为原理比较简单, 但性能较差, 所以 一般把直接插入排序,选择排序,冒泡排序归为简单排序一类, 另外四种排序都归于 改进排序
📚从平均情况看:
改进过的排序: 希尔排序, 堆排序, 归并排序, 快速排序要胜过简单排序的性能, 而四个改进算法中, 希尔排序的性能最差
📚时间复杂度:
直接插入排序和冒泡排序最快
📚从最好情况看从最坏情况看:
堆排序和归并排序的性能更胜过快排和其他简单排序
📚综合来看:
堆排序和归并排序比较稳定和强大, 情况最坏时好用
直接插入排序和冒泡排序, 最好情况时最好用,
而快速排序比较极端, 最好最坏情况都有缺陷 但是 快速排序能够称之为快速排序, 是因为它的综合性能最强💪,一般情况下是最快的
📚从稳定性来看:
改进排序中只有归并排序
📚从数据个数上看:
数据量越少, 越适合用简单排序, 因为堆排, 快速排序, 归并排序, 都用到了递归, 对于少量数据排序有点"炮弹打蚊子"
只要是交换时, 两数据相邻就是稳定的算法,只要是跳跃式的交换就是不稳定, 当然别忘了, 稳定的算法也可以修改代码更改成不稳定的
如果本篇对你有帮助,请点赞收藏支持一下,小手一抖就是对作者莫大的鼓励啦😋😋😋~
上山总比下山辛苦
下篇文章见
相关文章:

Java【归并排序】算法, 大白话式图文解析(附代码)
文章目录前言一、排序相关概念1, 什么是排序2, 什么是排序的稳定性3, 七大排序分类二、归并排序1, 图文解析2, 代码实现三、性能分析四、七大排序算法总体分析前言 各位读者好, 我是小陈, 这是我的个人主页 小陈还在持续努力学习编程, 努力通过博客输出所学知识 如果本篇对你有…...

【springboot】数据库访问
1、SQL 1、数据源的自动配置-HikariDataSource 1、导入JDBC场景 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-jdbc</artifactId></dependency>数据库驱动? 为什么导入JD…...

普通和hive兼容模式下sql的差异
–odps sql –– –author:宋文理 –create time:2023-03-08 15:23:52 –– – 差异分为三块 – 1.运算符的差异 – 2.类型转换的差异 – 3.内建函数的差异 – 以下是运算符的差异: – BITAND(&) – 当输入参数是BIGINT类型的时候&…...
github开源自己代码
接下来,我们需要先下载Git,的网址:https://git-scm.com/downloads,安装时如果没有特殊需求,一直下一步就可以了,安装完成之后,双击打开Git Bash 出现以下界面: 第一步:…...
数据库基础语法
sql(Structured Query Language 结构化查询语言) SQL语法 use DataTableName; 命令用于选择数据库。set names utf8; 命令用于设置使用的字符集。SELECT * FROM Websites; 读取数据表的信息。上面的表包含五条记录(每一条对应一个网站信息&…...
【Java】期末复习知识点总结(4)
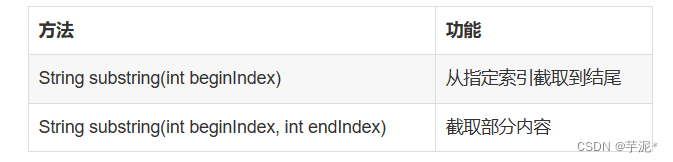
适合Java期末的复习~ (Java期末复习知识点总结分为4篇,这里是最后一篇啦)第一篇~https://blog.csdn.net/qq_53869058/article/details/129417537?spm1001.2014.3001.5501第二篇~https://blog.csdn.net/qq_53869058/article/details/1294751…...
IDEA好用插件:MybatisX快速生成接口实体类mapper.xml映射文件
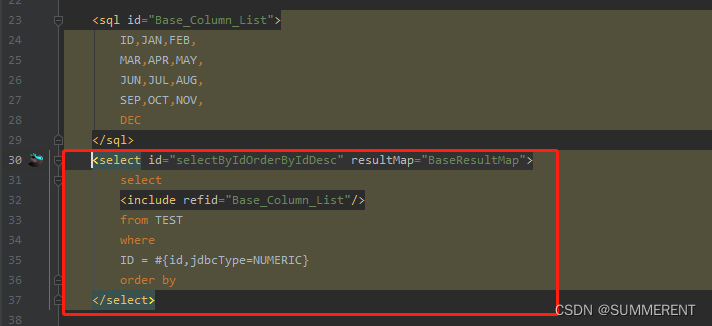
目录 1、在Idea中找到下载插件,Install,重启Idea 2、一个测试java文件,里面有com包 3、在Idea中添加数据库 --------以Oracle数据库为例 4、快速生成entity-service-mapper方法 5、查看生成的代码 6、自动生成(增删查改࿰…...

【JavaEE】初识线程
一、简述进程认识线程之前我们应该去学习一下“进程" 的概念,我们可以把一个运行起来的程序称之为进程,进程的调度,进程的管理是由我们的操作系统来管理的,创建一个进程,操作系统会为每一个进程创建一个 PCB&…...
智慧水务监控系统-智慧水务信息化平台建设
平台概述柳林智慧水务监控系统(智慧水务信息化平台)是以物联感知技术、大数据、智能控制、云计算、人工智能、数字孪生、AI算法、虚拟现实技术为核心,以监测仪表、通讯网络、数据库系统、数据中台、模型软件、前台展示、智慧运维等产品体系为…...
【Linux】进程优先级前后台理解
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹相关文章推荐:【Linux】冯.诺依曼体系结构与操作系统【Linux】进程理解与学习(Ⅰ)浅谈Linux下的shell--BASH【Linux…...
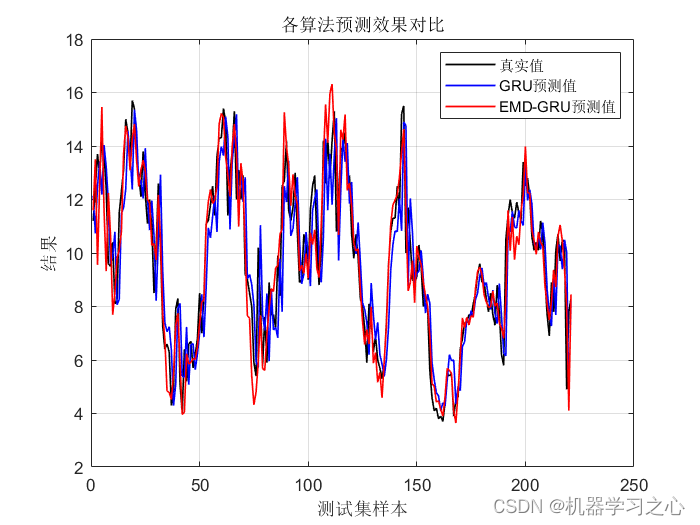
时序预测 | MATLAB实现基于EMD-GRU时间序列预测(EMD分解结合GRU门控循环单元)
时序预测 | MATLAB实现基于EMD-GRU时间序列预测(EMD分解结合GRU门控循环单元) 目录 时序预测 | MATLAB实现基于EMD-GRU时间序列预测(EMD分解结合GRU门控循环单元)效果一览基本描述模型描述程序设计参考资料效果一览...

python 模拟鼠标,键盘点击
信息爆炸 消息轰炸模拟鼠标和键盘敲击import time from pynput.keyboard import Controller as key_col from pynput.mouse import Button,Controller def keyboard_input(insertword):keyboardkey_col()keyboard.type(insertword)def mouth():mouseController()mouse.press(…...
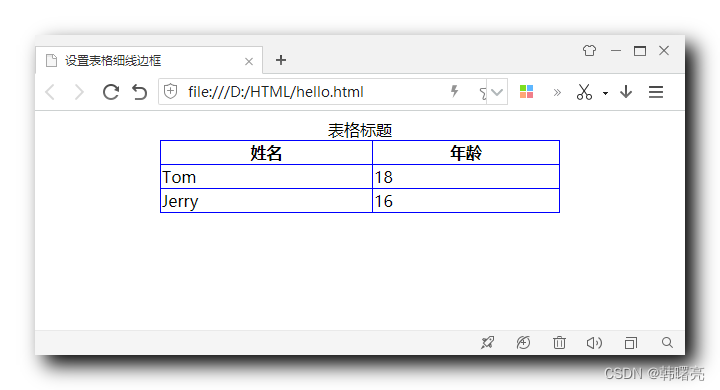
【CSS】盒子边框 ③ ( 设置表格细线边框 | 合并相邻边框 border-collapse: collapse; )
文章目录一、设置表格细线边框1、表格示例2、合并相邻边框3、完整代码示例一、设置表格细线边框 1、表格示例 给定一个 HTML 结构中的表格 , 默认样式如下 : <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8" />…...
)
TensorRT量化工具pytorch_quantization代码解析(一)
量化工具箱pytorch_quantization 通过提供一个方便的 PyTorch 库来补充 TensorRT ,该库有助于生成可优化的 QAT 模型。该工具包提供了一个 API 来自动或手动为 QAT 或 PTQ 准备模型。 API 的核心是 TensorQuantizer 模块,它可以量化、伪量化或收集张量的…...
【Kubernetes】第二十七篇 - 布署前端项(下)
一,前言 上一篇,介绍了前端项目的部署:项目的创建和 jenkins 配置; 本篇,创建 Deployment、Service,完成前端项目的部署; 二,创建 Deployment 创建 Deployment 配置文件ÿ…...
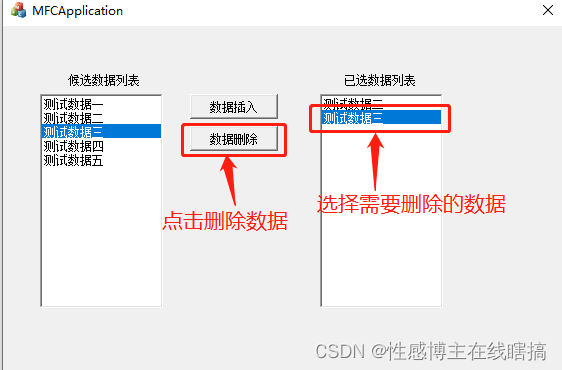
【MFC】两个ListBox控件数据交互
一.控件ID名称 界面如图下所示: 候选数据列表的ID为: 已选数据列表的ID为: 二.数据添加 可以使用以下代码往框中添加数据: ((CListBox *)GetDlgItem(IDC_LIST_TO_CHO))->AddString("测试数据"); 显示效果如下&#…...

sklearn库学习--SelectKBest 、f_regression
目录 一、SelectKBest 介绍、代码使用 介绍: 代码使用: 二、评分函数 【1】f_regression: (1)介绍: (2)F值和相关系数 【2】除了f_regression函数,还有一些适用于…...

蓝桥杯刷题第十三天
第一题:特殊日期问题描述对于一个日期,我们可以计算出年份的各个数位上的数字之和,也可以分别计算月和日的各位数字之和。请问从 1900 年 11 月 1 日至 9999 年 12 月 31 日,总共有多少天,年份的数位数字之和等于月的数…...

CPU 和带宽之间的时空权衡
在 从一道面试题看 TCP 的吞吐极限 一文的开始,我提到在环形域上两个数字比较大小的前提是在同一个半圆内,进而得到滑动窗口最大值被限定在一个环形域的一半。 现在来看更为基本的问题。如果序列号只有 2bit,甚至仅有 1bit,保序传…...
ES+Redis+MySQL,这个高可用架构设计太顶了!
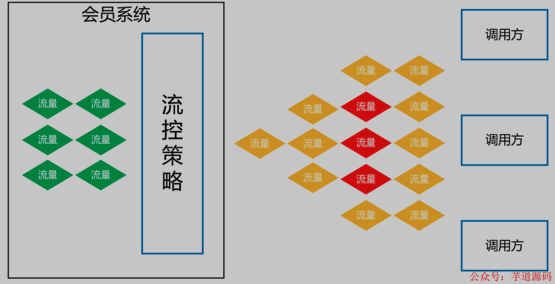
一、背景 会员系统是一种基础系统,跟公司所有业务线的下单主流程密切相关。如果会员系统出故障,会导致用户无法下单,影响范围是全公司所有业务线。所以,会员系统必须保证高性能、高可用,提供稳定、高效的基础服务。 …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
