FlinkModule加载HiveModule异常
HiveModule这个模块加载不出来

加在不出来这个模块,网上查说是要加下面这个依赖
<dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-hive_${scala.binary.version}</artifactId><version>${flink.version}</version>
</dependency>
先去我的本地maven仓库排查,发现这个包没下载下来

原因大概率是网络问题
可以删掉再次尝试,也可以改成下面这个依赖:
<dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-hive_2.12</artifactId><version>1.17.0</version> </dependency>
这样就没问题了,这个依赖和上面这个依赖的区别在于下面这个不需要scala环境。而且我写的代码本来就没有scala,所以不用上面这个依赖。

代码正常!
相关文章:

FlinkModule加载HiveModule异常
HiveModule这个模块加载不出来 加在不出来这个模块,网上查说是要加下面这个依赖 <dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-hive_${scala.binary.version}</artifactId><version>${flink.…...

计算机硬件---如何更新自己电脑的BLOS
1找官网 例如“我使用的是HP(惠普)品牌的电脑”我只需要在浏览器上搜索“惠普官网”或“惠普-blos更新” 就可以看到,来自官网中更新blos的信息 2.有些品牌要查序列号该怎么办呢? 有许多方法可以查询,例如…...

AI算法17-贝叶斯岭回归算法Bayesian Ridge Regression | BRR
贝叶斯岭回归算法简介 贝叶斯岭回归(Bayesian Ridge Regression)是一种回归分析方法,它结合了岭回归(Ridge Regression)的正则化特性和贝叶斯统计的推断能力。这种方法在处理具有大量特征的数据集时特别有用ÿ…...
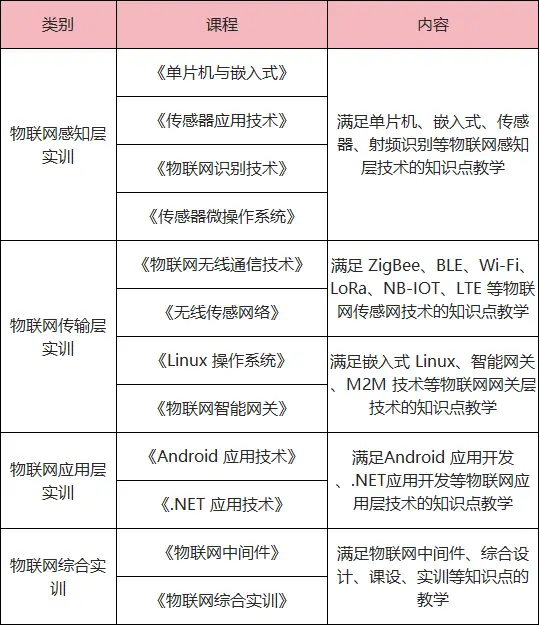
唯众物联网综合实训台 物联网实验室建设方案
物联网综合实训装置 物联网工程应用综合实训台是我公司针对职业院校物联网行业综合技能型人才培养,综合运用传感器技术、RFID技术、接口控制技术、无线传感网技术、Android应用开发等,配合实训台上的433M无线通信设备、ZigBee节点、射频设备、控制设备、…...

深入浅出 Vue.js:从基础到进阶的全面总结
深入浅出 Vue.js:从基础到进阶的全面总结 Vue.js 是一个用于构建用户界面的渐进式框架。它不仅易于上手,还能通过其强大的生态系统支持复杂的应用开发。本文将从基础到进阶,全面总结 Vue.js 的核心概念、常用技术和最佳实践,并提…...

路网双线合并单线——ArcGISpro 解决方法
路网双线合并成单线是一个在地图制作、交通规划以及GIS分析中常见的需求。双线路网定义:具有不同流向、不同平面结构的道路。此外,车道数较多的道路(例如,双黄实线车道数大于4的道路)也可以视为双线路网,本…...

邮箱验证码功能开发
该文章用于记录怎么进行邮箱验证码开发。 总所周知,我们在某些网站进行注册的适合总是会遇到什么填写邮箱,邮箱接收验证码,验证通过后才可以继续注册,那么这个功能是怎么实现的呢? 一,准备工作 1.1 邮箱…...
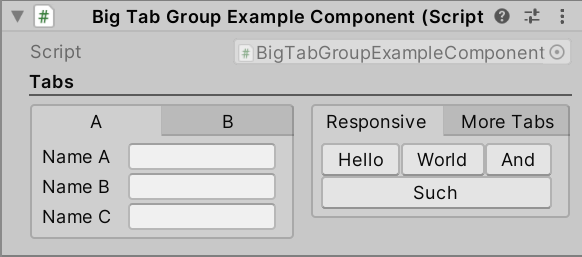
2024-07-15 Unity插件 Odin Inspector3 —— Button Attributes
文章目录 1 说明2 Button 特性2.1 Button2.2 ButtonGroup2.3 EnumPaging2.4 EnumToggleButtons2.5 InlineButton2.6 ResponsiveButtonGroup 1 说明 本文介绍 Odin Inspector 插件中有关 Button 特性的使用方法。 2 Button 特性 2.1 Button 依据方法,在 Inspec…...

根据脚手架archetype快速构建spring boot/cloud项目
1、找到archetype,并从私仓下载添加archetype到本地 点击IDEA的file,选择new project 选择maven项目,勾选create from archetype 填写archetype信息,(repository填写私仓地址) 2、选择自定义的脚手架arche…...

安灯系统在电力设备制造业中的应用效果
安灯系统作为面向制造业生产现场的专门应用软硬件系统,在电力设备制造企业中发挥着重要的作用。作为精益制造执行的核心工具,安灯系统为企业提供了快速联络生产、物料、维修、主管等部门的功能,以实时掌控和管理生产线状况,实现生…...

代码随想录打卡第二十五天
代码随想录–回溯部分 day 24 休息 day 25 回溯第三天 文章目录 代码随想录--回溯部分一、力扣93--复原IP地址二、力扣78--子集三、力扣90--子集Ⅱ 一、力扣93–复原IP地址 代码随想录题目链接:代码随想录 有效 IP 地址 正好由四个整数(每个整数位于 0…...

openharmony上传图片,并获取返回路径
适用条件: openharmony开发 4.0 release版本,对应能力API10 一直不断尝试,一会用官方提供的上传文件,一会用第三方库的axios都不行, 一会报错‘没权限,一会报错’路径错误,还有报错‘401参数错…...

git常用命令及git分支
git常用命令及git分支 git常用命令设置用户签名初始化本地库查看本地库状态将文件添加到暂存区提交到本地库查看历史记录版本穿梭 git分支什么是分支分支的好处分支的操作查看分支创建分支切换分支删除分支合并分支合并冲突 git常用命令 设置用户签名 //设置用户签名 git con…...

c# 依赖注入-服务的生命周期
在 C# 中,依赖注入服务的生命周期指的是在应用程序中管理和控制依赖项注入服务对象的生命周期的方式。常见的生命周期包括瞬态(transient)、作用域(scoped)和单例(singleton)三种。 瞬态&#…...

一站式短视频矩阵开发,高效托管!
短视频矩阵系统源码SaaS解决方案提供全面的开发服务,包括可视化视频编辑、矩阵式内容分发托管以及集成的多功能开发支持。 短视频矩阵:引爆您的数字营销革命 短视频矩阵系统是一套多功能集成解决方案,专为提升在短视频平台上的内容创作、管理…...

实践致知第16享:设置Word中某一页横着的效果及操作
一、背景需求 小姑电话说:现在有个word文档,里面有个表格太长(如下图所示),希望这一个设置成横的,其余页还是保持竖的! 二、解决方案 1、将鼠标放置在该页的最前面闪烁,然后选择“页面”》“↘…...

Leetcode—3011. 判断一个数组是否可以变为有序【中等】(__builtin_popcount()、ranges::is_sorted())
2024每日刷题(144) Leetcode—3011. 判断一个数组是否可以变为有序 O(n)复杂度实现代码 class Solution { public:bool canSortArray(vector<int>& nums) {// 二进制数位下1数目相同的元素就不进行组内排序// 只进行分组// 当前组的值若小于…...

盲盒一番赏小程序:开启惊喜之旅,探索无限创意!
在这个充满无限想象与惊喜的时代,盲盒已成为连接心灵与梦想的奇妙桥梁。为了将这份独特的乐趣与探索精神传递给每一位热爱生活、追求新鲜的你,我们自豪地推出了“盲盒一番赏”小程序——一个集创意、趣味、互动与社交于一体的盲盒新纪元,邀您…...

Linux基础知识之Linux文件系统权限
概述 文件权限控制对文件的访问可以针对文件所属用户、所属组和其他用户可以设置不同的权限权限具有优先级。user 权限覆盖 group 权限,后者覆盖 other 权限 权限:读取、写入和执行 权限 对文件的影响 对目录的影响 r (读取) 可以读取文件的内容 …...

Qt qml详细介绍
一.基本类型 QML的基本类型包括了很多不同的类型,这些类型可以用于定义用户界面元素、属性和信号。以下是一些常用的QML基本类型及其详细介绍: 数值类型:包括整数类型(int、uint、short、ushort等)和浮点数类型&#…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
