Leetcode 236. 二叉树的最近公共祖先
142. 环形链表 II
问题描述
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:

输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
- 链表中节点的数目范围在范围
[0, 104]内 -105 <= Node.val <= 105pos的值为-1或者链表中的一个有效索引
**进阶:**你是否可以使用 O(1) 空间解决此题?
解题思路与代码实现
解题思路I:
使用辅助集合存储访问过的节点:
如果有环,第一个遇到的访问过的节点即为入环的第一个节点;
如果无环,返回null;
class Solution {public ListNode detectCycle(ListNode head) {ListNode pos = head;Set<ListNode> visited = new HashSet<ListNode>(); // 记录访问过的节点while (pos != null) {if (visited.contains(pos)) {return pos;} else {visited.add(pos);}pos = pos.next;}return null;}
}
解题思路II:
- 先判断是否有环,使用快慢指针,初始时
fast和slow都指向head,fast指针每次走两步,slow指针每次走一步; - 如果有环,
fast移到head头结点,然后fast和slow每次都走一步,相遇时返回相遇节点; - 如果无环,则返回null。
public class Solution {public ListNode detectCycle(ListNode head) {if(head == null || head.next == null){ // 节点数量小于等于1,不可能有环return null;}// 快慢指针判断是否有环ListNode slow = head ,fast = head; while(fast!=null && slow!=null){slow = slow.next; // slow走一步fast = fast.next; // fast走两步if(fast!=null && fast.next != null){fast = fast.next;}else{ // fast 指针走过链表末端,说明链表无环,return null; }if(fast == slow){ // 二者指向同一节点fast = head;break;}}//有环while (fast != null){if (fast == slow ){return fast;}fast = fast.next;slow = slow.next;}return null;}
}
踩坑点
无
92. 反转链表 II
问题描述
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例 1:

输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
示例 2:
输入:head = [5], left = 1, right = 1
输出:[5]
提示:
- 链表中节点数目为
n 1 <= n <= 500-500 <= Node.val <= 5001 <= left <= right <= n
进阶: 你可以使用一趟扫描完成反转吗?
解题思路与代码实现
解题思路:
将链表划分为三部分:[1, left)、[left, right]、[right+1, n]
扫描链表,将[left, right]区间的中间链表反转后重新拼接
需要注意特殊的情况导致的NPE,如左链表不存在,右链表不存在
class Solution {/*** 反转从位置 left 到位置 right 的链表节点*/public ListNode reverseBetween(ListNode head, int left, int right) {if (head == null || head.next == null) { // 节点数不超过1的链表直接返回return head;}int count = 1; // 计数器ListNode cur = head; // 辅助指针ListNode leftHead = head, leftTail = null; // 左链表头尾结点while (cur != null && count < left) {leftTail = cur;cur = cur.next;count++;}if (leftTail != null) { // 左链表不为空leftTail.next = null;}ListNode midHead = cur, midTail = null; // 需要翻转的中间链表头尾结点while (cur != null && count <= right) {midTail = cur;cur = cur.next;count++;}if (midTail != null){midTail.next = null;}ListNode rightHead = cur; // 右链表的头结点ListNode[] nodes = reverseList(midHead); // 中间链表反转if ( leftTail == null) {leftHead = nodes[0];} else {leftTail.next = nodes[0];}nodes[1].next = rightHead;return leftHead;}/*** 反转链表,返回值包含反转后新链表的头尾节点*/private ListNode[] reverseList(ListNode head) {ListNode newTail = head, newHead = null; // 新链表的头尾节点ListNode current = head, post = null; // 辅助指针while (current != null) {post = current.next;current.next = newHead;newHead = current;current = post;}return new ListNode[]{newHead, newTail};}}
踩坑点
NPE
146. LRU 缓存
问题描述
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity)以 正整数 作为容量capacity初始化 LRU 缓存int get(int key)如果关键字key存在于缓存中,则返回关键字的值,否则返回-1。void put(int key, int value)如果关键字key已经存在,则变更其数据值value;如果不存在,则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示:
1 <= capacity <= 30000 <= key <= 100000 <= value <= 105- 最多调用
2 * 105次get和put
解题思路与代码实现
解题思路:
使用哈希表缓存键值对,使用双端队列实现LRU(最近最少使用)算法,最近最少访问的key放在队头,最新访问的key放在队尾。
调用get方法:若key存在,将key从双端队列中移除并重新添加到队尾;
调用put方法:
若key存在,更新value,同时将key从双端队列中移除并重新添加到队尾;
若key不存在:
如果缓存未满,直接插入到缓存中并将key保存到双端队列的队尾;
如果缓存已满,先从队头移除一个旧key,同时移除缓存;然后将新的key-value添加到缓存,并将key保存到双端队列的队尾。
class LRUCache {private HashMap<Integer, Integer> map = null; // 存储键值对private int capacity = 0; // 缓存容量private Deque<Integer> deque = null; // 辅助双端队列,实现lru算法,淘汰先入队的public LRUCache(int capacity) {this.capacity = capacity;map = new HashMap<>(capacity);deque = new LinkedList<>();}/*** 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1** @param key 关键字key*/public int get(int key) {if (map.containsKey(key)) {// key被访问,调整其在队列中的位置deque.remove(key);deque.addLast(key);return map.get(key);}return -1;}/*** 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。* 如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。** @param key 关键字* @param value 关键字对应的值*/public void put(int key, int value) {// 如果关键字 key 已经存在,则变更其数据值 valueif (map.containsKey(key)) {// 更新原有key在队列中的位置deque.remove(key);} else if (map.size() == capacity) { // key不存在且容量不充足// 找到最久未使用的关键字key移除Integer oldKey = deque.removeFirst();map.remove(oldKey);}// 入队deque.addLast(key);// 存在则更新,不存在则加入map.put(key, value);}
}
/*** Your LRUCache object will be instantiated and called as such:* LRUCache obj = new LRUCache(capacity);* int param_1 = obj.get(key);* obj.put(key,value);*/
踩坑点
236. 二叉树的最近公共祖先
问题描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
- 树中节点数目在范围
[2, 105]内。 -109 <= Node.val <= 109- 所有
Node.val互不相同。 p != qp和q均存在于给定的二叉树中。
解题思路与代码实现
解题思路:
解题思路是通过递归后序遍历二叉树,查找节点 p 和 q 的最近公共祖先。如果当前节点为 null 或者是 p 或 q 中的一个,直接返回当前节点。递归地在左右子树中查找 p 和 q,并根据返回结果判断:
- 如果左子树返回
null,右子树返回null,则p和q不在当前树中,返回null。 - 如果左子树返回非
null,右子树返回null,则p和q都在左子树中,返回左子树的结果。 - 如果左子树返回
null,右子树返回非null,则p和q都在右子树中,返回右子树的结果。 - 如果左右子树分别返回非
null,则当前节点即为p和q的最近公共祖先,返回当前节点。
class Solution {/*** 返回p、q在root树中的最近公共祖先*/public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 当root为null或者p、q之一为root时,返回rootif (root == null || root == p || root == q) {return root;}// 后序遍历TreeNode left = lowestCommonAncestor(root.left, p, q);TreeNode right = lowestCommonAncestor(root.right, p, q);if (left == null && right == null) { // p或q不在root树中return null;} else if (left == null) { // 在右子树中找到了p、qreturn right;} else if (right == null) { // 左子树中找到了p、qreturn left;} else { // p、q分别在左右子树中return root;}}
}
踩坑点
124. 二叉树中的最大路径和
问题描述
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:

输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:

输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
解题思路与代码实现
解题思路:
通过递归后序遍历二叉树来求解节点及其子树的最大路径和。
在递归过程中,空节点视为0,对于每个节点,计算其左右子树的最大路径和(如果为负数则视作0),然后更新全局变量 res,记录可能的最大路径和,最后返回以当前节点为根的子树中包含当前节点的最大路径和。
class Solution {private int res = Integer.MIN_VALUE; // 记录全局最大路径和/*** 返回以root为根节点的子树中的最大路径和* @param root 当前节点* @return 当前节点及其子树的最大路径和*/public int maxPathSum(TreeNode root) {postOrder(root); // 调用后序遍历函数return res; // 返回最大路径和}/*** 后序遍历递归函数,计算以当前节点为根的子树的最大路径和* @param root 当前节点* @return 当前节点及其子树的最大贡献值(即单侧最大路径和)*/private int postOrder(TreeNode root) {if (root == null) { // 如果当前节点为空,返回0return 0;}// 计算左右子树的最大贡献值,小于0的贡献值视为0int leftVal = Math.max(0, postOrder(root.left));int rightVal = Math.max(0, postOrder(root.right));// 更新全局最大路径和res = Math.max(res, leftVal + rightVal + root.val);// 返回当前节点及其子树的最大贡献值(单侧最大路径和)return root.val + Math.max(leftVal, rightVal);}
}踩坑点
373. 查找和最小的 K 对数字
问题描述
给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v),其中第一个元素来自 nums1,第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。
示例 1:
输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数:[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
示例 2:
输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释: 返回序列中的前 2 对数:[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]
提示:
1 <= nums1.length, nums2.length <= 105-109 <= nums1[i], nums2[i] <= 109nums1和nums2均为 升序排列1 <= k <= 104k <= nums1.length * nums2.length
解题思路与代码实现
解题思路:
初始时将所有的 (i,0) 对入堆,这是因为 (i,0) 对应的数对是数组 nums1 的前 k 个元素与 nums2 的第一个元素的和,这些是最小的数对之一。
在每次从堆中取出数对 (i,j) 后,将 (i,j+1) 入堆。这是因为 (i,j+1) 对应的数对是数组 nums1[i] 和 nums2[j+1] 的和,可能成为下一个可能的最小数对。这样做可以保证堆中始终是当前可能的最小数对集合,确保了答案的正确性和最小性。
class Solution {/*** 返回两个数组 nums1 和 nums2 中前 k 个最小的数对* @param nums1 第一个数组* @param nums2 第二个数组* @param k 最小数对的个数* @return 前 k 个最小数对的列表*/public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {List<List<Integer>> ans = new ArrayList<>(k); // 预分配空间PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]); // 小顶堆// 初始将所有 (i,0) 入堆,其中 i 为 0 到 nums1.length - 1for (int i = 0; i < Math.min(nums1.length, k); i++) {pq.add(new int[] { nums1[i] + nums2[0], i, 0 });}// 依次取出堆中最小的数对,加入结果列表,同时将其下一个数对 (i, j+1) 入堆while (ans.size() < k && !pq.isEmpty()) {int[] p = pq.poll(); // 取出当前最小的数对int i = p[1];int j = p[2];ans.add(List.of(nums1[i], nums2[j])); // 加入结果列表// 如果 nums2 中仍有下一个元素,将其与 nums1[i] 的和入堆if (j + 1 < nums2.length) {pq.add(new int[] { nums1[i] + nums2[j + 1], i, j + 1 });}}return ans; // 返回前 k 个最小数对的列表}
}踩坑点
暴力枚举所有组合导致超时
530. 二叉搜索树的最小绝对差
问题描述
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例 1:

输入:root = [4,2,6,1,3]
输出:1
示例 2:

输入:root = [1,0,48,null,null,12,49]
输出:1
提示:
- 树中节点的数目范围是
[2, 104] 0 <= Node.val <= 105
解题思路与代码实现
解题思路:
二叉搜索树的性质,中序遍历的数组是升序排列的。
所以最小绝对值差必然在|根节点值-左子树最大值| 和|根节点值-右子树最小值|,在中序遍历数组中它们三者是相邻的。
public int getMinimumDifference(TreeNode root) {int res = Integer.MAX_VALUE; // 初始化最小绝对差为最大整数Integer pre = null; // 用于记录中序遍历时前一个节点的值// 非递归中序遍历二叉搜索树Stack<TreeNode> stack = new Stack<>(); // 辅助栈TreeNode cur = root; // 辅助指针while (cur != null || !stack.isEmpty()) {if (cur != null) {stack.push(cur);cur = cur.left; // 往左子树遍历} else {TreeNode node = stack.pop(); // 弹出栈顶节点if (pre != null) {res = Math.min(res, Math.abs(pre - node.val)); // 更新最小绝对差}pre = node.val; // 更新前一个节点的值为当前节点的值cur = node.right; // 遍历右子树}}return res;}
踩坑点
相关文章:

Leetcode 236. 二叉树的最近公共祖先
142. 环形链表 II 问题描述 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环&am…...

GPT-4从0到1搭建一个Agent简介
GPT-4从0到1搭建一个Agent简介 1. 引言 在人工智能领域,Agent是一种能够感知环境并采取行动以实现特定目标的系统。本文将简单介绍如何基于GPT-4搭建一个Agent。 2. Agent的基本原理 Agent的核心是感知-行动循环(Perception-Action Loop)…...

docker镜像源配置
docker默认的镜像源,走的是国外网络,下载速度感人,修改镜像源,进入/etc/docker/ cd /etc/docker 编辑文件daemon.json(没有就直接创建),内容: {"registry-mirrors": ["https://q7ta64ip.…...
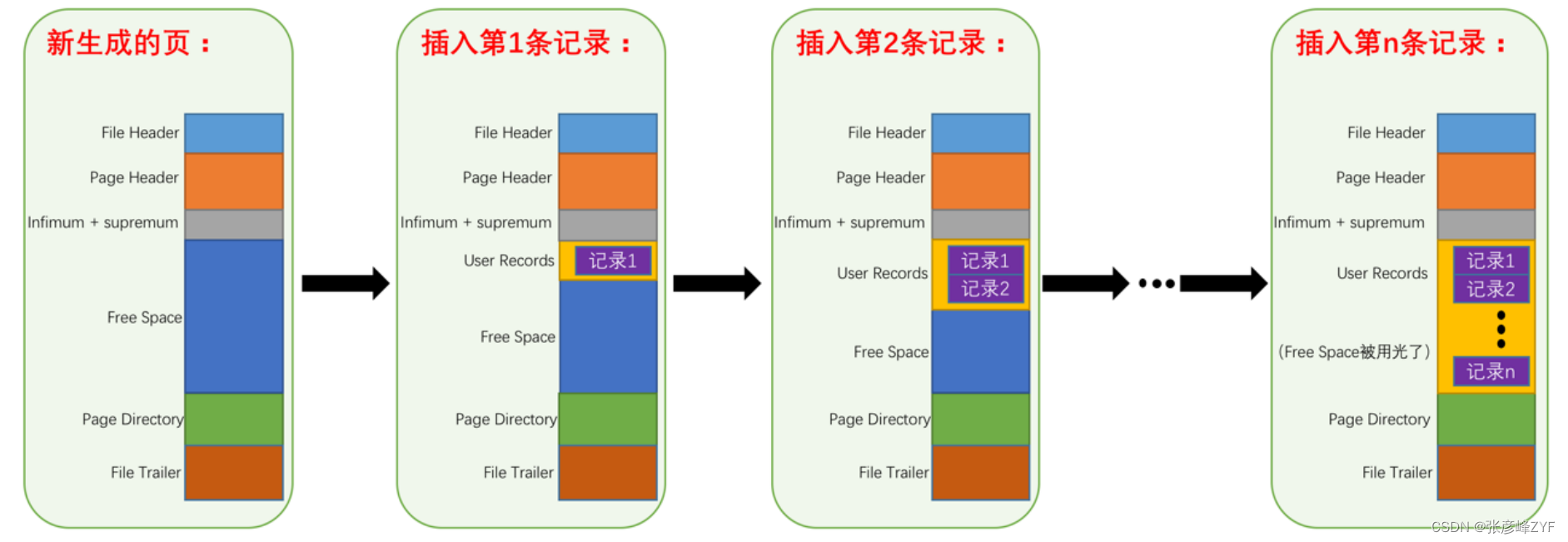
解读InnoDB数据库索引页与数据行的紧密关联
目录 一、快速走进索引页结构 (一)整体展示说明 (二)内容说明 File Header(文件头部) Page Header(页面头部) Infimum Supremum(最小记录和最大记录) …...

以数据编织,重构数据管理新范式
大数据产业创新服务媒体 ——聚焦数据 改变商业 人工智能几乎统一了全球最顶尖科技公司的认知:这个时代,除了AI,没有第二条路可走。 人工智能的技术逻辑颇有一种“暴力美学”,它依托于海量大数据和超高算力的训练和推理ÿ…...

在linux x86服务器安装jdk
安装JDK(Java Development Kit)在Linux x86 服务器上可以按照以下步骤进行操作。以下步骤假设你有root权限或者sudo权限。 1. 下载JDK安装包 首先,你需要从Oracle官网或者OpenJDK官网下载JDK的安装包。可以选择对应的版本,比如J…...

2024智慧竞技游戏俱乐部线下面临倒闭?
在2024年的中国,智慧竞技游戏俱乐部如雨后春笋般在二三线城市中兴起,它们不仅是年轻人娱乐的场所,更是智慧与技巧的较量场。然而,随着疫情的冲击,这些俱乐部面临着前所未有的挑战。本文将通过一个小镇上的故事…...

jmeter分布式(四)
一、gui jmeter的gui主要用来调试脚本 1、先gui创建脚本 先做一个脚本 演示:如何做混合场景的脚本? 用211的业务比例 ①启动数据库服务 数据库服务:包括mysql、redis mysql端口默认3306 netstat -lntp | grep 3306处于监听状态…...

如何解决手机游戏因IP代理被封禁无法正常游戏的问题?
在当前的网络环境下,许多手机游戏为了维护游戏的公平性和安全性,会采取措施对使用IP代理的玩家进行封禁,导致他们无法正常访问游戏。这种情况对于一些需要使用IP代理的用户来说可能显得很棘手,但实际上有几种技术性的解决方案可以…...

windows10 安装Anaconda
文章目录 1. 下载2. 安装3. 配置环境变量4. 检查是否安装成功 1. 下载 官网下载 https://www.anaconda.com/download 下载的最新版本,要求python的版本也高一些 清华大学开源软件镜像站 https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 所有版本在这个网…...

[图解]SysML和EA建模住宅安全系统-14-黑盒系统规约
1 00:00:02,320 --> 00:00:07,610 接下来,我们看下一步指定黑盒系统需求 2 00:00:08,790 --> 00:00:10,490 就是说,把这个系统 3 00:00:11,880 --> 00:00:15,810 我们的目标系统,ESS,看成黑盒 4 00:00:18,030 --> …...

frp内网穿透xtcp安全点对点p2p部署记录打洞失败解决方法
环境 一、有公网IP、nas主机(需要穿透里面的服务)、安卓手机、frps-0.58.1、frpc-0.59.0(群晖NAS套件)、安卓版frpc-0.56.0 二、两端frpc必须要有一端nat网络类型不是非对称nat 开始 有公网的主机上配置frps.toml bindPort 7000nas主机端frpc.toml配…...

C++基础篇(2)
目录 前言 1.缺省参数 2.函数重载 2.1函数重载的基本规则 编辑2.2注意事项 2.3 重载解析(Overload Resolution)--补充内容 3.引用 3.1引用的概念和定义 3.2引用的特性 3.3引用的使用 3.4const引用 4.指针和引用的关系 结束语 前言 上节小编…...

c++ primer plus 第16章string 类和标准模板库,16.1.3 使用字符串
c primer plus 第16章string 类和标准模板库,16.1.3 使用字符串 c primer plus 第16章string 类和标准模板库,16.1.3 使用字符串 文章目录 c primer plus 第16章string 类和标准模板库,16.1.3 使用字符串16.1.3 使用字符串程序清单16.3 hangman.cpp 16.1.3 使用字符串 现在&a…...

使用mybatis的statementHander拦截器监控表和字段并发送钉钉消息
新建mybatis的statementHander拦截器拦截器 类 面试题: 2.实现 解析Sql时引入JSqlParser JSqlParser 是一个 SQL 语句解析器。 它将 SQL转换为可遍历的 Java 类层次结构。 <dependency><groupId>com.github.jsqlparser</groupId><artifac…...
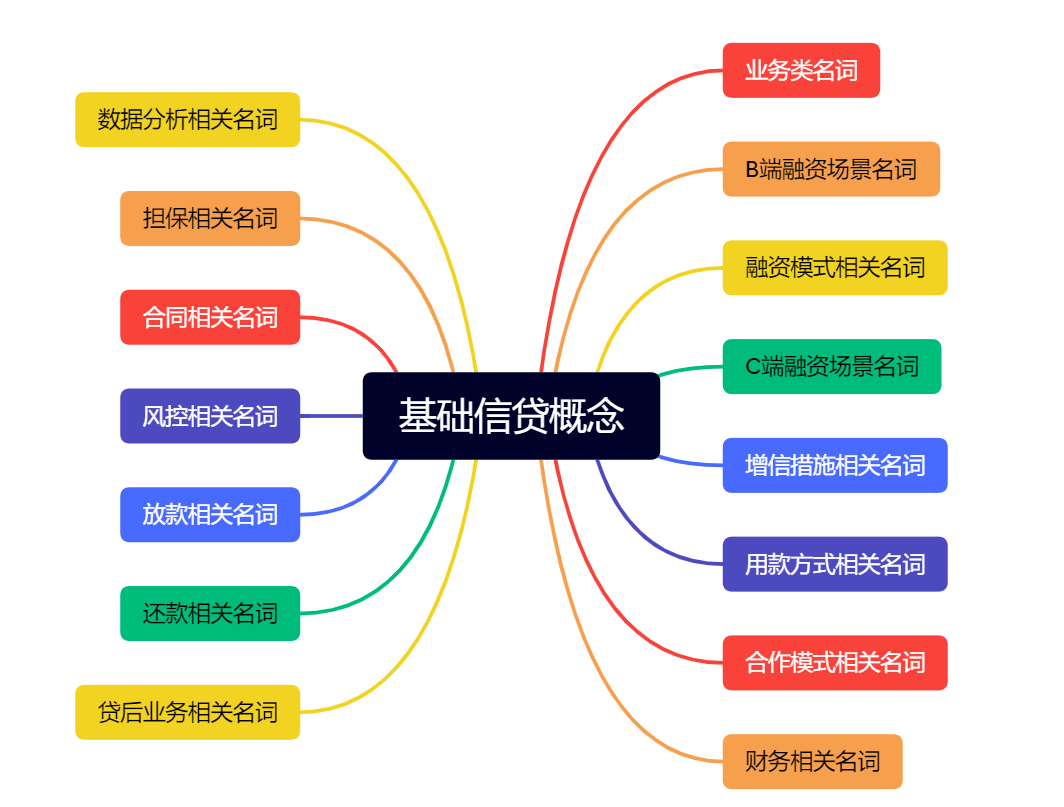
信贷系统——基础信贷概念
摘要 信贷是金融领域中的一个重要概念,指的是金融机构(如银行、信用合作社等)向个人、企业或政府提供资金的过程。在信贷过程中,金融机构向借款人提供资金,借款人则承诺在未来的某个时间点按照约定的条件和利率偿还借款。这种借款通常是在合同中明确约定的,包括贷款金额、…...
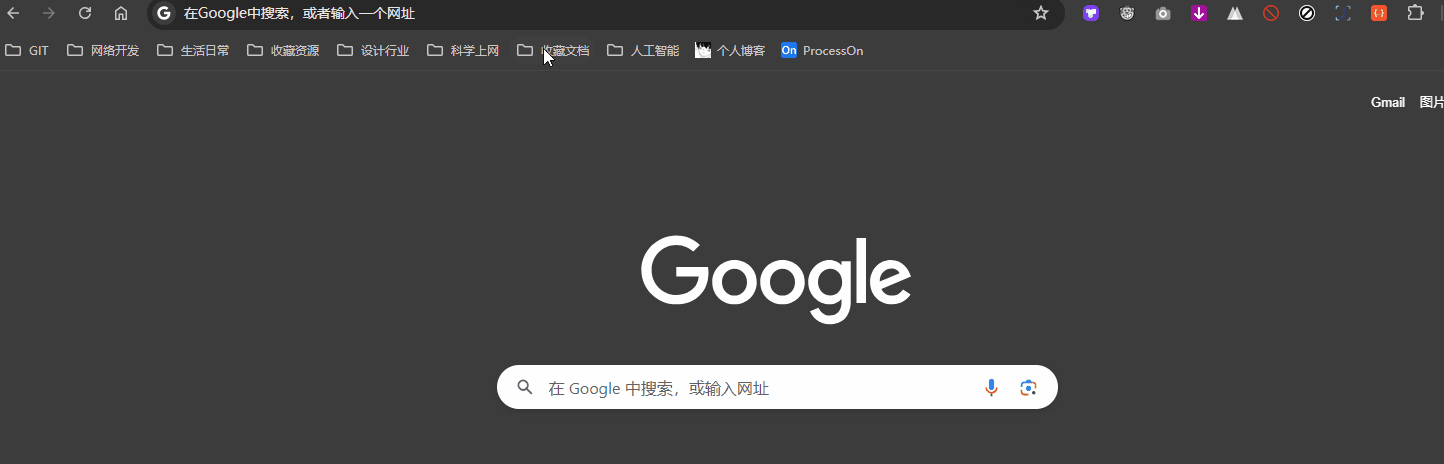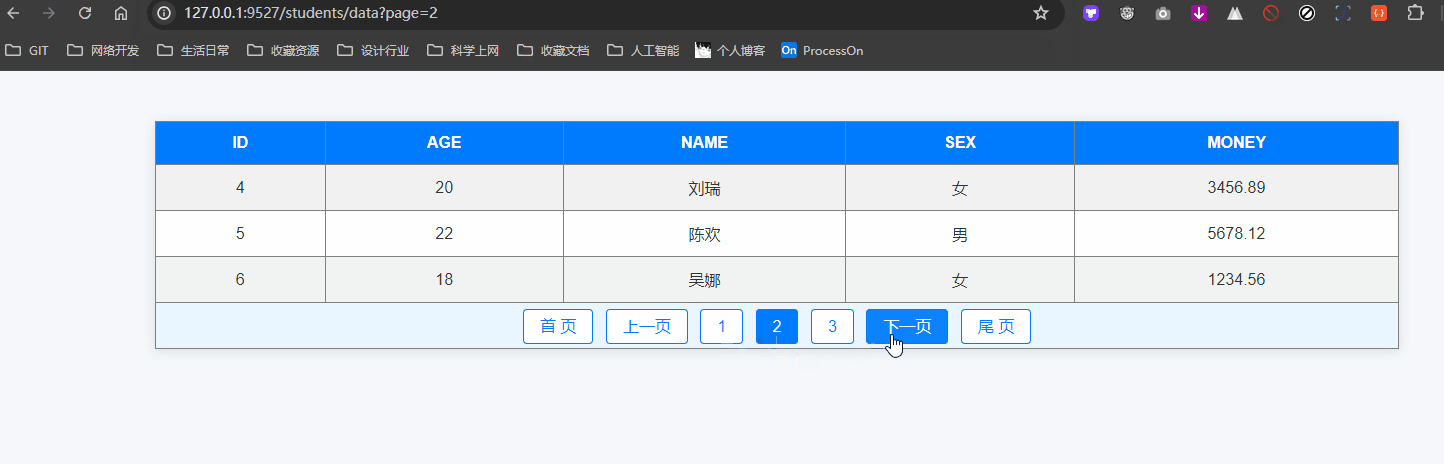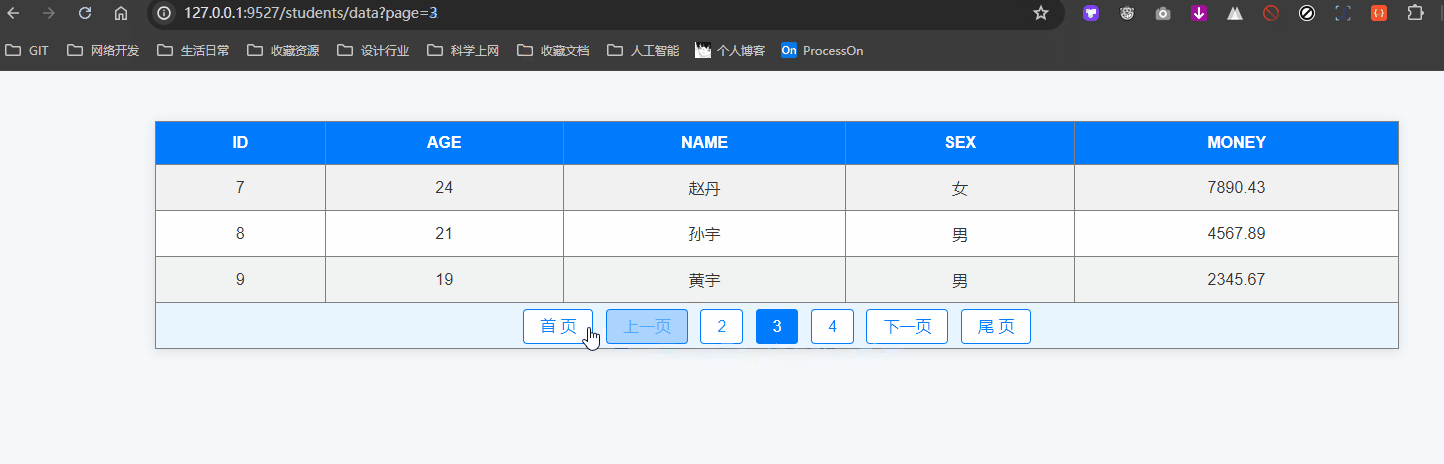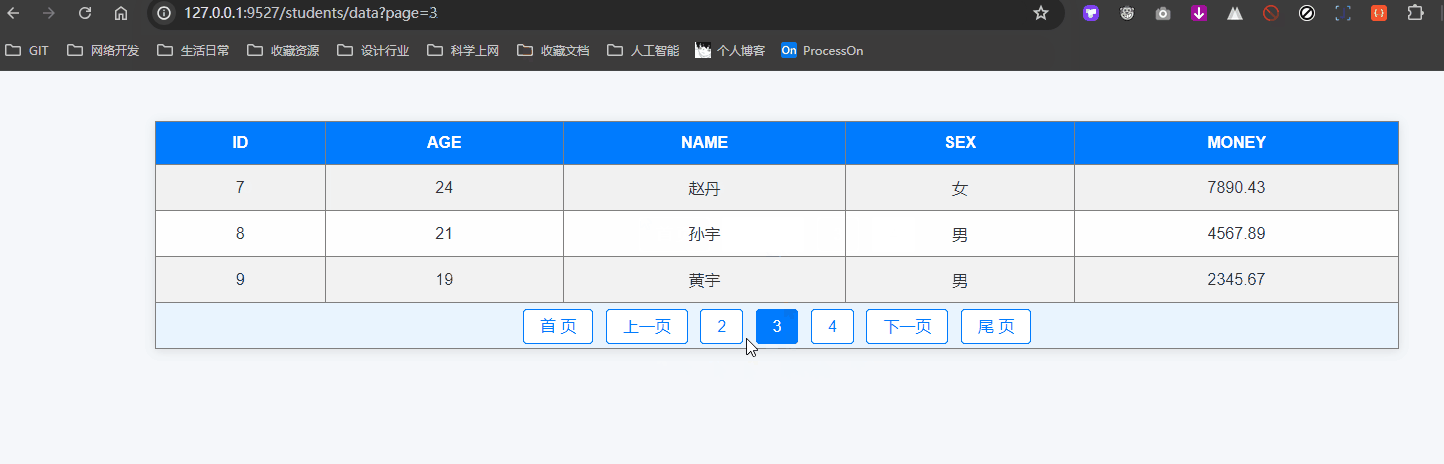
分页查询及其拓展应用案例
分页查询 分页查询是处理大量数据时常用的技术,通过分页可以将数据分成多个小部分,方便用户逐页查看。SQLAlchemy 提供了简单易用的方法来实现分页查询。 本篇我们也会在最终实现这样的分页效果: 1. 什么是分页查询 分页查询是将查询结果按照…...

【UE5.1】NPC人工智能——02 NPC移动到指定位置
效果 步骤 1. 新建一个蓝图,父类选择“AI控制器” 这里命名为“BP_NPC_AIController”,表示专门用于控制NPC的AI控制器 2. 找到我们之前创建的所有NPC的父类“BP_NPC” 打开“BP_NPC”,在类默认值中,将“AI控制器类”一项设置为“…...

有关电力电子技术的一些相关仿真和分析:⑤交-直-交全桥逆变+全波整流结构电路(MATLAB/Siumlink仿真)
全桥逆变+全波整流结构 参数:Vin=500V, Vo=200V, T=2:1:1, RL=10Ω, fs=100kHz, L=1mH, C=100uF (1)给定输入电压,输出电压和主电路参数,仿真研究电路工作原理,分析工作时序; (2)调节负载电阻,实现电流连续和断续,并仿真验证; (3)调节占空比,分析占空比与电…...

记录一次Android推流、录像踩坑过程
背景: 按照需求,需要支持APP在手机息屏时进行推流、录像。 技术要点: 1、手机在息屏时能够打开camera获取预览数据 2、获取预览数据时进行编码以及合成视频 一、息屏时获取camera预览数据: ①Camera.setPreviewDisplay(SurfaceH…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
