Open3D 最小二乘法拟合点云平面
目录
一、概述
1.1最小二乘法原理
1.2实现步骤
1.3应用场景
二、代码实现
2.1关键函数
2.2完整代码
三、实现效果
3.1原始点云
3.2matplotlib可视化
3.3平面拟合方程
前期试读,后续会将博客加入该专栏,欢迎订阅
Open3D点云算法与点云深度学习案例汇总(长期更新)-CSDN博客
一、概述
1.1最小二乘法原理
最小二乘法(Least Squares Method)是一种用于数据拟合的数学优化方法,通过最小化误差平方和来找到最佳拟合参数。在拟合平面时,我们使用最小二乘法来确定平面方程的参数,使得点云数据中的点到该平面的垂直距离的平方和最小。
1.2实现步骤

1.3应用场景
- 计算机视觉和图像处理:在物体表面拟合、3D重建和立体视觉中,帮助理解物体的几何形状和结构。
- 地理信息系统(GIS)和遥感:在地形建模和分析中,用于生成数字高程模型(DEM)和分析地貌特征。
- 机器人学和导航:在路径规划和SLAM中,帮助机器人感知环境并进行定位和导航。
- 工程和结构分析:在土木工程和建筑中,用于测量建筑物和结构物的平整度和倾斜度。
- 医学图像处理:在医学成像中,用于分析器官和组织的表面特征,辅助诊断和治疗
二、代码实现
2.1关键函数
在 fit_plane_least_squares 函数中,我们将点云数据的 x 和 y 坐标以及一个常数 1 作为矩阵 A,将 z 坐标作为向量 b。求解线性系统后,我们获得了平面的参数 a, b 和 d。平面方程为 ax + by + cz + d = 0,因此 c = -1
def fit_plane_least_squares(points):"""使用最小二乘法直接求解拟合点云平面。参数:points (numpy.ndarray): 点云数据,形状为 (N, 3)。返回:plane (tuple): 平面参数 (a, b, c, d),其中 ax + by + cz + d = 0。"""# 构建矩阵 A 和向量 bA = np.c_[points[:, :2], np.ones(points.shape[0])]b = points[:, 2]# 求解线性系统 A^T A [a, b, d]^T = A^T bx, residuals, rank, s = np.linalg.lstsq(A, b, rcond=None)# 返回平面参数 (a, b, c, d)a, b, d = xc = -1.0 # 平面法向量的z分量return a, b, c, d2.2完整代码
import open3d as o3d
import numpy as np
import matplotlib.pyplot as pltdef fit_plane_least_squares(points):"""使用最小二乘法直接求解拟合点云平面。参数:points (numpy.ndarray): 点云数据,形状为 (N, 3)。返回:plane (tuple): 平面参数 (a, b, c, d),其中 ax + by + cz + d = 0。"""# 构建矩阵 A 和向量 bA = np.c_[points[:, :2], np.ones(points.shape[0])]b = points[:, 2]# 求解线性系统 A^T A [a, b, d]^T = A^T bx, residuals, rank, s = np.linalg.lstsq(A, b, rcond=None)# 返回平面参数 (a, b, c, d)a, b, d = xc = -1.0 # 平面法向量的z分量return a, b, c, ddef plot_fitted_plane(points, plane_params):"""绘制点云和拟合平面的网格。参数:points (numpy.ndarray): 点云数据,形状为 (N, 3)。plane_params (tuple): 平面参数 (a, b, c, d),其中 ax + by + cz + d = 0。"""A, B, C, D = plane_params# 检查 C 值,避免除零错误if np.isclose(C, 0):C = 1e-10fig1 = plt.figure()ax1 = fig1.add_subplot(111, projection='3d')ax1.set_xlabel("x")ax1.set_ylabel("y")ax1.set_zlabel("z")# 获取xyz坐标及最值用于plot绘图min_pt = np.amin(points, axis=0) # 获取坐标最小值max_pt = np.amax(points, axis=0) # 获取坐标最大值ax1.scatter(points[:, 0], points[:, 1], points[:, 2], c='r', marker='^')# 创建拟合的平面网格x_p = np.linspace(min_pt[0], max_pt[0], 100)y_p = np.linspace(min_pt[1], max_pt[1], 100)XFit, YFit = np.meshgrid(x_p, y_p)ZFit = -(D + A * XFit + B * YFit) / C# 绘制拟合平面网格ax1.plot_wireframe(XFit, YFit, ZFit, rstride=10, cstride=10)# 显示图像plt.show()# -----------------------------读取点云--------------------------------
pcd = o3d.io.read_point_cloud("tilted_plane_noise.pcd")# 检查并移除 NaN 和无穷大值
pcd = pcd.remove_non_finite_points()# ----------------基于最小二乘法直接求解的拟合平面-----------------------
points = np.asarray(pcd.points) # 获取点云数据
plane_params = fit_plane_least_squares(points)
A, B, C, D = plane_params
print('平面拟合结果为:%.6f * x + %.6f * y + %.6f * z + %.6f = 0' % (A, B, C, D))# 调用绘制网格平面的函数
plot_fitted_plane(points, plane_params)
三、实现效果
3.1原始点云

3.2matplotlib可视化

3.3平面拟合方程
平面拟合结果为:-0.004528 * x + 0.363171 * y + -1.000000 * z + 0.002728 = 0相关文章:

Open3D 最小二乘法拟合点云平面
目录 一、概述 1.1最小二乘法原理 1.2实现步骤 1.3应用场景 二、代码实现 2.1关键函数 2.2完整代码 三、实现效果 3.1原始点云 3.2matplotlib可视化 3.3平面拟合方程 前期试读,后续会将博客加入该专栏,欢迎订阅 Open3D点云算法与点云深度学习…...

【Django+Vue3 线上教育平台项目实战】登录功能模块之短信登录与钉钉三方登录
文章目录 前言一、几个关键概念1.HTTP无状态性2.Session机制3.Token认证4.JWT 二、通过手机号验证码登录1.前端短信登录界面2.发送短信接口与短信登录接口3.Vue 设置interceptors拦截器4. 服务端验证采用自定义中间件方式实现5. 操作流程及效果图如下: 三、通过第三…...

关于HBase、Phoenix、Flume、Maxwell 和 Flink
组件协同: HBase HBase 是一个分布式的、列存储的NoSQL数据库,它基于Google的Bigtable设计,特别适合存储海量的、稀疏的、非结构化或半结构化数据。HBase 提供了低延迟的随机读写能力,但其原生接口和数据模型较为复杂࿰…...

centos7停止维护,可替代的操作系统
CentOS 7 将在 2024 年 6 月 30 日停止维护。如果你目前正在使用 CentOS 7,可以考虑以下几种替代的操作系统: 1. CentOS Stream CentOS Stream 是 CentOS 项目的一个新版本,它提供了一个滚动发布的 Linux 发行版。CentOS Stream 位于 Fedor…...

andon系统在电力设备工管理中起到那些作用与价值
安灯系统,作为精益制造执行中的一个核心工具,在电力设备工厂车间管理中发挥着不可替代的作用,它能够实现生产透明管理,为工厂高效运作提供强大的支撑。本文将从安灯系统的功能、应用场景和价值三个方面,深入探讨其在电…...

消息队列-RabbitMQ
消息队列-RabbitMQ 1、RabbitMQ是什么?2、RabbitMQ的业务场景有哪些?3、RabbitMQ中有哪基本概念?4、RabbitMQ有哪些工作模式?5、如何保证RabbitMQ消息顺序性?6、RabbitMQ消息如何分发?7、RabbitMQ消息怎么路由?8、为什么会产生重复消费?如何保证消息不被重复消费(如何…...
集群监控)
Elasticsearch(ES)集群监控
Elasticsearch(ES)集群监控 在Elasticsearch中,监控集群的健康状况、性能和运行指标是至关重要的。以下是一些常用的Elasticsearch监控工具和API的例子: 使用Elasticsearch自带的API来获取集群健康状态、节点信息和统计信息。 # 获取集群健康状况 curl…...

图像处理:使用 OpenCV-Python 卡通化你的图像(2)
一、说明 在图像处理领域,将图像卡通化是一种新趋势。人们使用不同的应用程序将他们的图像转换为卡通图像。如今,玩弄图像是许多人的爱好。人们通常会点击图片并添加滤镜或使用不同的东西自定义图像并将其发布到社交媒体上。但我们是程序员,…...

淘宝扭蛋机小程序:旋转惊喜,开启购物新篇章!
在追求创新与惊喜的购物时代,淘宝再次引领潮流,精心打造——淘宝扭蛋机小程序,为您的购物之旅增添一抹不同寻常的色彩。这不仅仅是一个购物工具,更是一个充满趣味、互动与惊喜的宝藏盒子,等待您来探索与发现。 【旋转…...

JAVA零基础小白自学日志——第十七天
文章目录 1.方法的覆写2.类的层次结构3.如何判定正确的继承顺序4.如何判断子类继承(继承这个词我始终觉得很变扭)了父类的什么5.继承关系的实质6.关键字:super 和 this[1].this关键字(1)this关键字调用本类属性&#x…...
和app.on(‘ready‘)的区别)
electron中app.whenReady()和app.on(‘ready‘)的区别
app.whenReady和app.on(‘ready’)都是用于在Electron应用程序中处理初始化完成事件的方法。app.whenReady是一个返回Promise的方法,它会在应用程序准备好创建窗口时解决。一旦app.whenReady被调用,就可以安全地创建窗口,因为此时Electron的初…...

技术速递|Let’s Learn .NET Aspire – 开始您的云原生之旅!
作者:James Montemagno 排版:Alan Wang Let’s Learn .NET 是我们全球性的直播学习活动。在过去 3 年里,来自世界各地的开发人员与团队成员一起学习最新的 .NET 技术,并参加现场研讨会学习如何使用它!最重要的是&#…...

JSONNode树形解析或流式解析
哈喽,大家好,我是木头左! 什么是JSONNode? JSONNode是一个用于处理JSON数据的数据结构,它提供了一种简单、灵活、高效的方式来操作JSON数据。JSONNode可以看作是一个树形结构,其中每个节点都可以包含一个值…...

自制迷宫游戏 c++
竞赛的同时也不能忘记娱乐,劳逸结合,我们自研了迷宫游戏,只能在DEV C 运行哦 #include<bits/stdc.h> #include<iomanip> #include<iostream> #include<cstdlib> #include<ctime> #include<conio.h> #include<win…...

基于复旦微JFMQL100TAI的全国产化FPGA+AI人工智能异构计算平台,兼容XC7Z045-2FFG900I
基于上海复旦微电子FMQL45T900的全国产化ARM核心板。该核心板将复旦微的FMQL45T900(与XILINX的XC7Z045-2FFG900I兼容)的最小系统集成在了一个87*117mm的核心板上,可以作为一个核心模块,进行功能性扩展,能够快速的搭建起…...

【数学建模】技术革新——Lingo的使用超详解
目录 基础知识 1. 变量声明 示例 2. 常量声明 语法格式 示例 3. 目标函数 语法格式 示例 4. 约束条件 语法格式 示例 5. 完整的Lingo模型示例 示例 解释 6. 整数变量声明 语法格式 示例 7. 非线性规划 示例 8. 多目标优化 语法格式 示例 9. 数据输入与…...
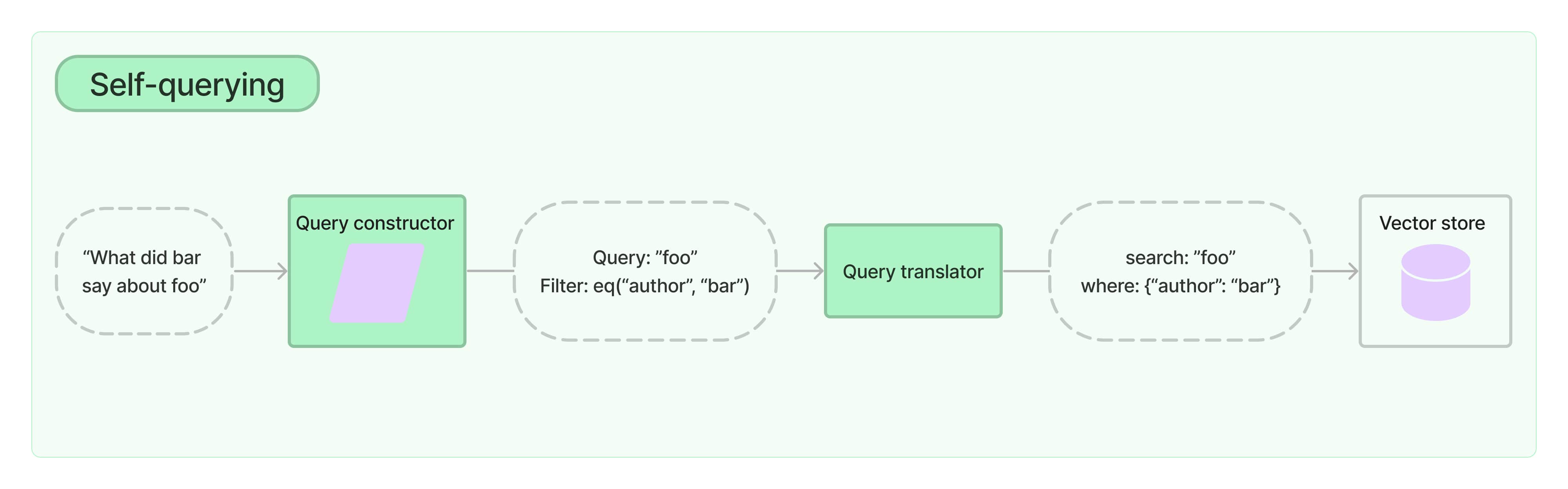
LLM-阿里 DashVector + langchain self-querying retriever 优化 RAG 实践【Query 优化】
文章目录 前言self querying 简介代码实现总结 前言 现在比较流行的 RAG 检索就是通过大模型 embedding 算法将数据嵌入向量数据库中,然后在将用户的查询向量化,从向量数据库中召回相似性数据,构造成 context template, 放到 LLM 中进行查询…...

【python】PyQt5的窗口界面的各种交互逻辑实现,轻松掌控图形化界面程序
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

DockerCompose介绍,安装,使用
DockerCompose 1、Compose介绍 将单机服务-通过Dockerfile 构建为镜像 -docker run 成为一个服务 user 8080 net 7000 pay 8181 admin 5000 监控 .... docker run 单机版、一个个容器启动和停止问题: 前面我们使用Docker的时候,定义 Dockerfil…...

N叉树的前序遍历
Problem: 589. N 叉树的前序遍历 文章目录 思路解题过程Code 思路 前序遍历,遇到空节点返回 解题过程 对每个节点进行遍历 Code /* // Definition for a Node. class Node { public:int val;vector<Node*> children;Node() {}Node(int _val) {val _val;}Nod…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
