JSONNode树形解析或流式解析
哈喽,大家好,我是木头左!
什么是JSONNode?
JSONNode是一个用于处理JSON数据的数据结构,它提供了一种简单、灵活、高效的方式来操作JSON数据。JSONNode可以看作是一个树形结构,其中每个节点都可以包含一个值和一个子节点列表。通过遍历这个树形结构,可以方便地访问和修改JSON数据。
JSONNode树形解析
树形解析是一种将JSON数据转换为树形结构的方法。在这种方法中,首先将JSON数据转换为一个根节点,然后递归地将每个子节点添加到父节点的子节点列表中。这样,就可以通过遍历树形结构来访问和修改JSON数据。
以下是一个简单的树形解析示例:
public static void parseJson(JSONNode root) {if (root.isObject()) {for (String key : root.fieldNames()) {JSONNode child = root.get(key);if (child.isObject()) {parseJson(child);} else if (child.isArray()) {for (int i = 0; i < child.size(); i++) {parseJson(child.get(i));}} else {System.out.println("Key: " + key + ", Value: " + child);}}} else if (root.isArray()) {for (int i = 0; i < root.size(); i++) {parseJson(root.get(i));}} else {System.out.println("Value: " + root);}
}
在这个示例中,首先检查根节点是否是一个对象。如果是,遍历它的所有字段,并递归地解析每个子节点。如果当前子节点是一个对象,继续递归;如果它是一个数组,遍历数组并递归地解析每个元素;否则,打印出键和值。如果根节点是一个数组,遍历数组并递归地解析每个元素;否则,打印出值。
JSONNode流式解析
流式解析是一种将JSON数据转换为流式结构的方法。在这种方法中,不需要一次性将整个JSON数据加载到内存中,而是逐个处理JSON数据的每个元素。这样,可以更高效地处理大型JSON数据。
以下是一个简单的流式解析示例:
public static void parseJsonStream(InputStream inputStream) throws IOException {BufferedReader reader = new BufferedReader(new InputStreamReader(inputStream));String line;while ((line = reader.readLine()) != null) {// 在这里处理每一行JSON数据,例如将其解析为一个JSONNode对象}
}
在这个示例中,使用BufferedReader从输入流中读取每一行JSON数据。然后,可以将每一行JSON数据解析为一个JSONNode对象,或者直接对其进行处理。这样,就可以逐个处理JSON数据的每个元素,而不需要将整个JSON数据加载到内存中。
JSONNode树形解析与流式解析的比较
JSONNode树形解析和流式解析各有优缺点。下面简要比较一下这两种方法:
优点
- 树形解析:树形解析可以让更方便地访问和修改JSON数据。通过遍历树形结构,可以很容易地找到任何节点及其子节点。此外,树形解析还可以让更容易地实现一些复杂的操作,例如查找、排序等。
- 流式解析:流式解析可以让更高效地处理大型JSON数据。由于不需要一次性将整个JSON数据加载到内存中,因此流式解析可以节省大量内存资源。此外,流式解析还可以让更容易地处理实时生成的JSON数据。
缺点
- 树形解析:树形解析的缺点是需要将整个JSON数据加载到内存中。对于大型JSON数据,这可能会导致内存不足的问题。此外,树形解析还需要消耗一定的CPU资源来构建和维护树形结构。
- 流式解析:流式解析的缺点是处理起来相对复杂。由于需要逐个处理JSON数据的每个元素,因此可能需要编写更多的代码来实现相同的功能。此外,流式解析可能无法提供像树形解析那样直观的访问和修改JSON数据的方式。
JSONNode树形解析与流式解析的应用场景
根据不同的应用场景,可以选择合适的JSONNode树形解析或流式解析方法。以下是一些常见的应用场景:
- 需要对JSON数据进行复杂操作的场景:在这些场景中,需要对JSON数据进行复杂的操作,例如查找、排序等。这时,树形解析可能是更好的选择,因为它可以让更方便地访问和修改JSON数据。
- 需要处理大型JSON数据的场景:在这些场景中,需要处理大型JSON数据,但内存资源有限。这时,流式解析可能是更好的选择,因为它可以让更高效地处理大型JSON数据,而不需要将整个JSON数据加载到内存中。
- 需要实时处理JSON数据的场景:在这些场景中,需要实时处理生成的JSON数据。这时,流式解析可能是更好的选择,因为它可以让更容易地处理实时生成的JSON数据。
- 需要简化代码的场景:在这些场景中,希望简化代码的编写和维护。这时,可以根据具体需求选择合适的方法。如果树形解析可以使代码更简洁,那么可以选择树形解析;如果流式解析可以使代码更简洁,那么可以选择流式解析。
我是木头左,感谢各位童鞋的点赞、收藏,我们下期更精彩!

相关文章:

JSONNode树形解析或流式解析
哈喽,大家好,我是木头左! 什么是JSONNode? JSONNode是一个用于处理JSON数据的数据结构,它提供了一种简单、灵活、高效的方式来操作JSON数据。JSONNode可以看作是一个树形结构,其中每个节点都可以包含一个值…...

自制迷宫游戏 c++
竞赛的同时也不能忘记娱乐,劳逸结合,我们自研了迷宫游戏,只能在DEV C 运行哦 #include<bits/stdc.h> #include<iomanip> #include<iostream> #include<cstdlib> #include<ctime> #include<conio.h> #include<win…...

基于复旦微JFMQL100TAI的全国产化FPGA+AI人工智能异构计算平台,兼容XC7Z045-2FFG900I
基于上海复旦微电子FMQL45T900的全国产化ARM核心板。该核心板将复旦微的FMQL45T900(与XILINX的XC7Z045-2FFG900I兼容)的最小系统集成在了一个87*117mm的核心板上,可以作为一个核心模块,进行功能性扩展,能够快速的搭建起…...

【数学建模】技术革新——Lingo的使用超详解
目录 基础知识 1. 变量声明 示例 2. 常量声明 语法格式 示例 3. 目标函数 语法格式 示例 4. 约束条件 语法格式 示例 5. 完整的Lingo模型示例 示例 解释 6. 整数变量声明 语法格式 示例 7. 非线性规划 示例 8. 多目标优化 语法格式 示例 9. 数据输入与…...
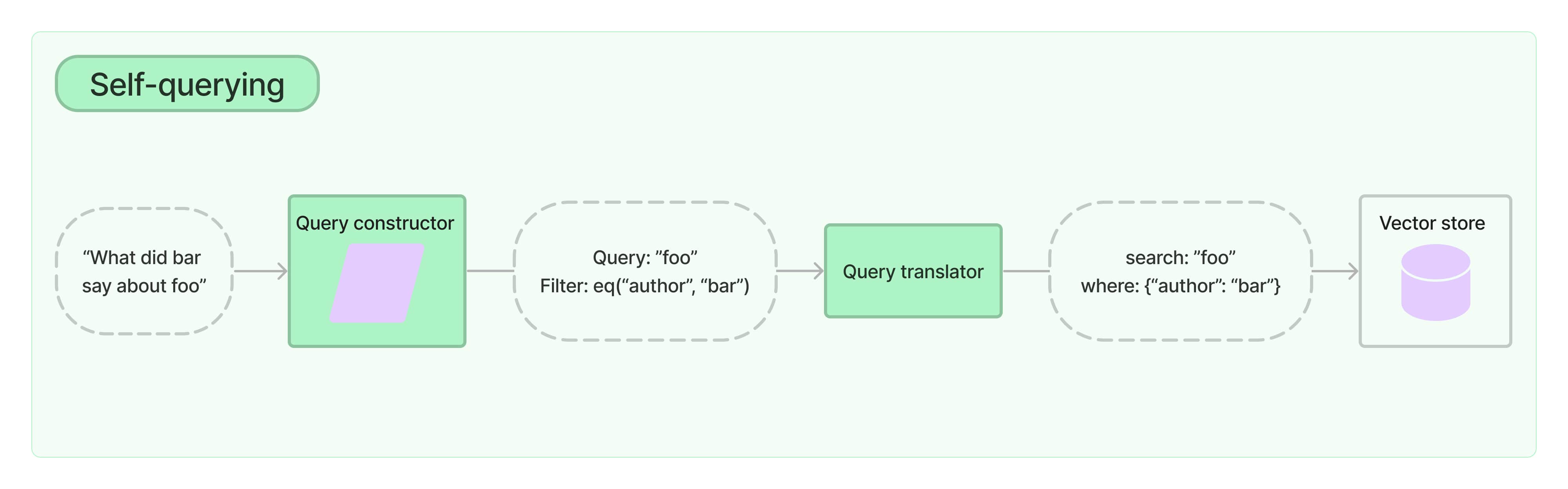
LLM-阿里 DashVector + langchain self-querying retriever 优化 RAG 实践【Query 优化】
文章目录 前言self querying 简介代码实现总结 前言 现在比较流行的 RAG 检索就是通过大模型 embedding 算法将数据嵌入向量数据库中,然后在将用户的查询向量化,从向量数据库中召回相似性数据,构造成 context template, 放到 LLM 中进行查询…...

【python】PyQt5的窗口界面的各种交互逻辑实现,轻松掌控图形化界面程序
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

DockerCompose介绍,安装,使用
DockerCompose 1、Compose介绍 将单机服务-通过Dockerfile 构建为镜像 -docker run 成为一个服务 user 8080 net 7000 pay 8181 admin 5000 监控 .... docker run 单机版、一个个容器启动和停止问题: 前面我们使用Docker的时候,定义 Dockerfil…...

N叉树的前序遍历
Problem: 589. N 叉树的前序遍历 文章目录 思路解题过程Code 思路 前序遍历,遇到空节点返回 解题过程 对每个节点进行遍历 Code /* // Definition for a Node. class Node { public:int val;vector<Node*> children;Node() {}Node(int _val) {val _val;}Nod…...

Linux C++ 054-设计模式之外观模式
Linux C 054-设计模式之外观模式 本节关键字:Linux、C、设计模式、外观模式 相关库函数: 概念 外观模式(Facade),亦称“过程模式”。主张按照描述和判断资料来评价课程,关键的活动是在课程实施的全过程中…...

Linux - 冯-诺依曼体系结构、初始操作系统
目录 冯•诺依曼体系 结构推导 内存提高效率的方法 数据的流动过程 体系结构相关知识 初始操作系统 定位 设计目的 操作系统之上之下分别有什么 管理精髓:先描述,再组织 冯•诺依曼体系 结构推导 计算机基本工作流程图大致如下: 输入设备&a…...

成功适配!极验设备指纹HarmonyOS 鸿蒙版官方下载
近日,华为开发者大会(HDC 2024)在东莞召开。在大会开幕日的首场主题演讲中,华为宣布当前已有TOP5000应用成为鸿蒙原生应用,350+SDK已适配HarmonyOS NEXT版本。其中,极验作为其重要伙伴ÿ…...

【C++】字符串学习 知识点+代码记录
一.知识点总结 1. C风格字符串(字符数组) 字符数组存储字符串:C风格的字符串实际上是字符数组,以空字符\0作为结尾标志。字符串字面量与字符数组:字符串字面量如"Hello"被编译器视为const char*类型&#…...

尝试理解docker网络通信逻辑
一、docker是什么 Docker本质是一个进程,宿主机通过namespace隔离机制提供进程需要运行基础环境,并且通过Cgroup限制进程调用资源。Docker的隔离机制包括 network隔离,此次主要探讨网络隔离mount隔离hostname隔离user隔离pid隔离进程通信隔离 二、doc…...
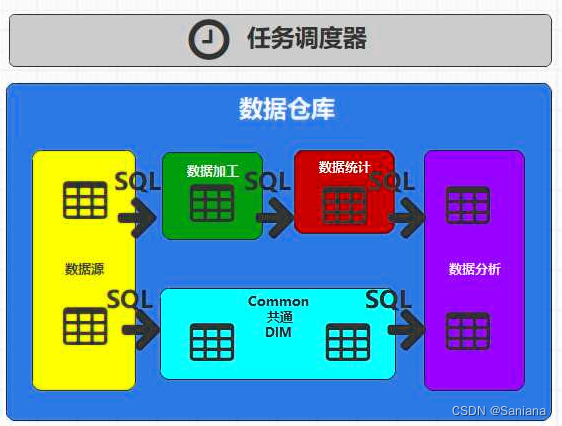
数据仓库哈哈
数据仓库 基本概念数据库(database)和数据仓库(Data Warehouse)的异同 整体架构分层架构方法论ER模型(建模理论)维度模型 何为分层第一层:数据源(ODS ER模型)设计要点日志…...

K最近邻(K-Nearest Neighbors, KNN)
K最近邻(K-Nearest Neighbors, KNN)理论知识推导 KNN算法是一个简单且直观的分类和回归方法,其基本思想是:给定一个样本点,找到训练集中与其最近的K个样本点,根据这些样本点的类别(分类问题&am…...

深度学习损失计算
文章目录 深度学习损失计算1.如何计算当前epoch的损失?2.为什么要计算样本平均损失,而不是计算批次平均损失? 深度学习损失计算 1.如何计算当前epoch的损失? 深度学习中的损失计算,通常为数据集的平均损失࿰…...

论文翻译:通过云计算对联网多智能体系统进行预测控制
通过云计算对联网多智能体系统进行预测控制 文章目录 通过云计算对联网多智能体系统进行预测控制摘要前言通过云计算实现联网的多智能体控制系统网络化多智能体系统的云预测控制器设计云预测控制系统的稳定性和一致性分析例子结论 摘要 本文研究了基于云计算的网络化多智能体预…...

Java核心(五)多线程
线程并行的逻辑 一个线程问题 起手先来看一个线程问题: public class NumberExample {private int cnt 0;public void add() {cnt;}public int get() {return cnt;} }public static void main(String[] args) throws InterruptedException {final int threadSiz…...

IDEA快速生成项目树形结构图
下图用的IDEA工具,但我觉得WebStorm 应该也可以 文章目录 进入项目根目录下,进入cmd输入如下指令: 只有文件夹 tree . > list.txt 包括文件夹和文件 tree /f . > list.txt 还可以为相关包路径加上注释...

【CPO-TCN-BiGRU-Attention回归预测】基于冠豪猪算法CPO优化时间卷积双向门控循环单元融合注意力机制
基于冠豪猪算法CPO(Correlation-Preservation Optimization)优化的时间卷积双向门控循环单元(Bidirectional Gated Recurrent Unit,BiGRU)融合注意力机制(Attention)的回归预测需要详细的实现和…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
