518. 零钱兑换 II ——【Leetcode每日一题】
518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10]
输出:1
提示:
- 1 <= coins.length <= 300
- 1 <= coins[i] <= 5000
- coins 中的所有值 互不相同
- 0 <= amount <= 5000
思路:
此问题属于 0-1背包 的 完全背包 ,解法和 0-1背包类似:
0 - 1背包问题(万能统一代码)
定义一个二维数组dp 存储硬币组合数,其中 dp[i][j] 表示前 i 个硬币 可以凑成总金额 为 j 的 硬币组合数:
- 每种硬币的数量是无限的,所以可以重复使用
- 状态转移方程为:
dp[i][j]=dp[i−1][j]+dp[i][j−coins[i]]dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]]dp[i][j]=dp[i−1][j]+dp[i][j−coins[i]]
示例1 的dp二维数组为:
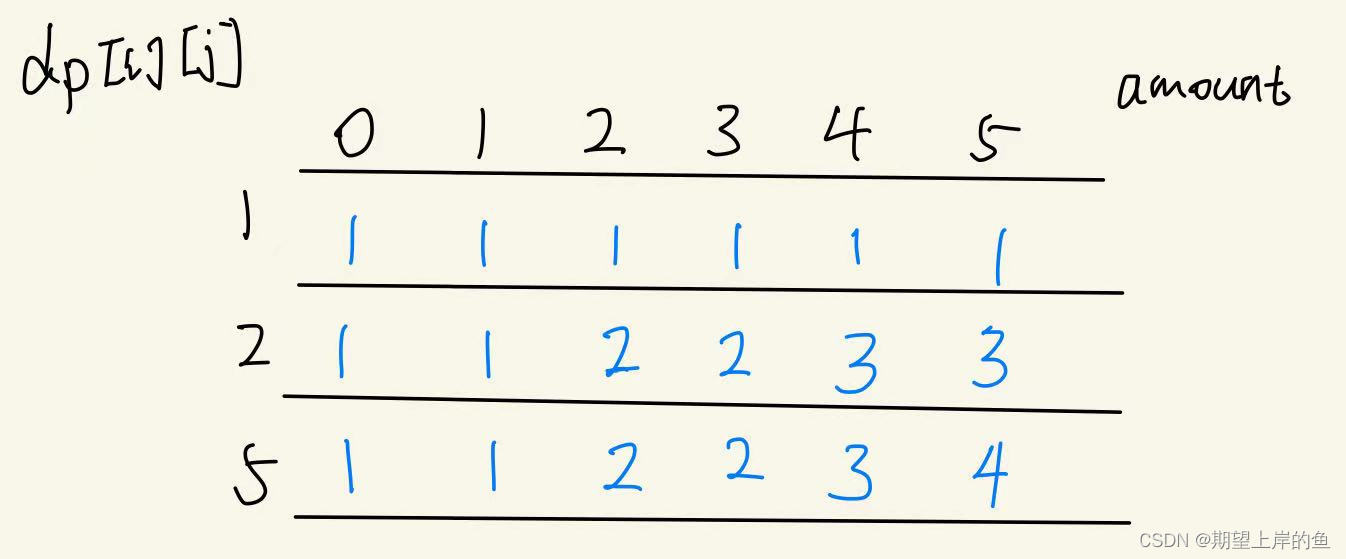
观察前 i 个硬币的状态仅与前 i -1 个硬币的状态有关,因此可以优化,将 dp 定义为一维数组,其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i ][j - coins[i]]:状态转移方程为:
dp[j]+=dp[j−coins[i]]dp[j] += dp[j - coins[i]]dp[j]+=dp[j−coins[i]]
代码:(Java)
public class Change {public static void main(String[] args) {// TODO Auto-generated method stubint[] coins = {1, 2, 5};int amount = 5;System.out.println(change(amount, coins));}public static int change(int amount, int[] coins) {int[] dp = new int[amount + 1];dp[0] = 1;for(int coin : coins) {for(int i = coin; i <= amount; i++) {dp[i] += dp[i - coin];}}return dp[amount];}
}
运行结果:

复杂度分析:
- 时间复杂度:O(len∗amount)O(len * amount)O(len∗amount), lenlenlen 为数组 coinscoinscoins 的长度,amountamountamount 为要凑成的总金额。
- 空间复杂度:O(amount)O(amount)O(amount) ,需要开辟一个一维数组 dp , 长度为amount+1amount + 1amount+1 ,amountamountamount 为要凑成的总金额。
322. 零钱兑换 I
注:仅供学习参考 如有不足,欢迎指正!
题目来源:力扣。
相关文章:

518. 零钱兑换 II ——【Leetcode每日一题】
518. 零钱兑换 II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 3…...

django DRF请求访问频率限制
Django REST framework(DRF)提供了一个throttle_classes属性,可以用于限制API的访问频率。它可以防止恶意用户发送大量请求以消耗服务器资源。使用throttle_classes属性,需要在settings.py中配置REST_FRAMEWORK:REST_F…...

二分查找创新性总结
LeetCode题目 704.二分查找35.搜索插入位置69.x 的平方根367.有效的完全平方数34.在排序数组中查找元素的第一个和最后一个位置 二分查找适用范围 可随机访问的数据结构数据已经有序要查找的值只有一个 上述的前四题都可直接使用二分查找,第五题要求查找上限和下限&…...

Java Web 实战 13 - 多线程进阶之 synchronized 原理以及 JUC 问题
文章目录一 . synchronized 原理1.1 synchronized 使用的锁策略1.2 synchronized 是怎样自适应的? (锁膨胀 / 升级 的过程)1.3 synchronized 其他的优化操作锁消除锁粗化1.4 常见面试题二 . JUC (java.util.concurrent)2.1 Callable 接口2.2 ReentrantLock2.3 原子类2.4 线程池…...
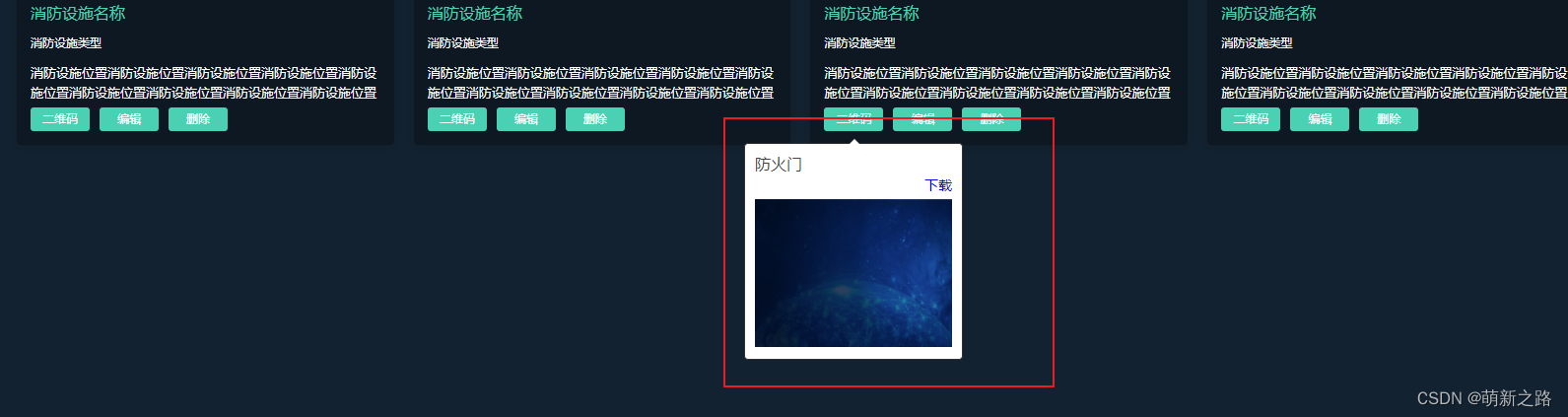
【解决】elementui ——tooltip提示在循环中点击一个,同时显示多个的问题!
同时显示多个tooltip——效果图: 点击第一个二维码把循环el-card中所有的tooltip都触发了 解决后效果图: 只显示点击的当前tooltip 解决办法: 通过循环item中定义字段,进行控制tooltip显示隐藏 代码: 页面代码&am…...
SpringBoot-核心技术篇
技术掌握导图 六个大标题↓ 配置文件web开发数据访问单元测试指标指控原理解析 配置文件 1.文件类型 1.1、properties 同以前的properties用法 1.2、yaml 1.2.1、简介 YAML是 “YAML Aint Markup Language”(YAML不是一种标记语言)的递归缩写。在…...

2023还有人不知道kubernetes?| 初步理解kubernetes
文章目录Kubernetes(K8s)一、Openstack&VM1、**认识虚拟化****1.1**、什么是虚拟化**1.2、虚拟化分类**2、OpenStack与KVM、VMWare2.1、OpenStack2.2、KVM2.3、VMWare二、容器&编排技术1、容器发展史1.1、Chroot1.2、FreeBSD Jails1.3、Solaris Zones1.4、LXC1.5、Dock…...

Docker 环境搭建
RabbitMq 安装与启动安装:运行命令:docker pull rabbitmq 默认版本是:latest启动rabbitmq:运行命令:docker run \ # 运行-e RABBITMQ_DETAULT_USERroot \ # 设置用户名-e RABBITMQ_DETAULT_PASS123456 \ # 设置 密码--…...

css实现炫酷充电动画
先绘制一个电池,电池头部和电池的身体 这里其实就是两个div,使用z-index改变层级,电池的身体盖住头部,圆角使用border-radius完成 html部分,完整的css部分在最后 <div class"chargerBox"><div class"ch…...

【Effective C++详细总结】第二章 构造/析构/赋值运算
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📚专栏地址:C/C知识点 📣专栏定位:整理一下 C 相关的知识点,供大家学习参考~ ❤️如果有收获的话,欢迎点赞👍…...

webpack基础
webpack基础 webpack基础目录webpack基础前言Webpack 是什么?Webpack 有什么用?一、webpack的基本使用webpack如何使用文件和文件夹创建创建文件下载依赖二、基本配置5 大核心概念准备 Webpack 配置文件修改配置文件处理样式资源处理图片资源修改输出资源…...

jQuery《一篇搞定》
今日内容 一、JQuery 零、 复习昨日 1 写出至少15个标签 2 写出至少7个css属性font-size,color,font-familytext-algin,background-color,background-image,background-sizewidth,heighttop,bottom ,left ,rightpositionfloatbordermarginpadding 3 写出input标签的type的不…...
Spring Cloud学习笔记【负载均衡-Ribbon】
文章目录什么是Spring Cloud RibbonLB(负载均衡)是什么Ribbon本地负载均衡客户端 VS Nginx服务端负载均衡区别?Ribbon架构工作流程Ribbon Demo搭建IRule规则Ribbon负载均衡轮询算法的原理配置自定义IRule新建MyRuleConfig配置类启动类添加Rib…...
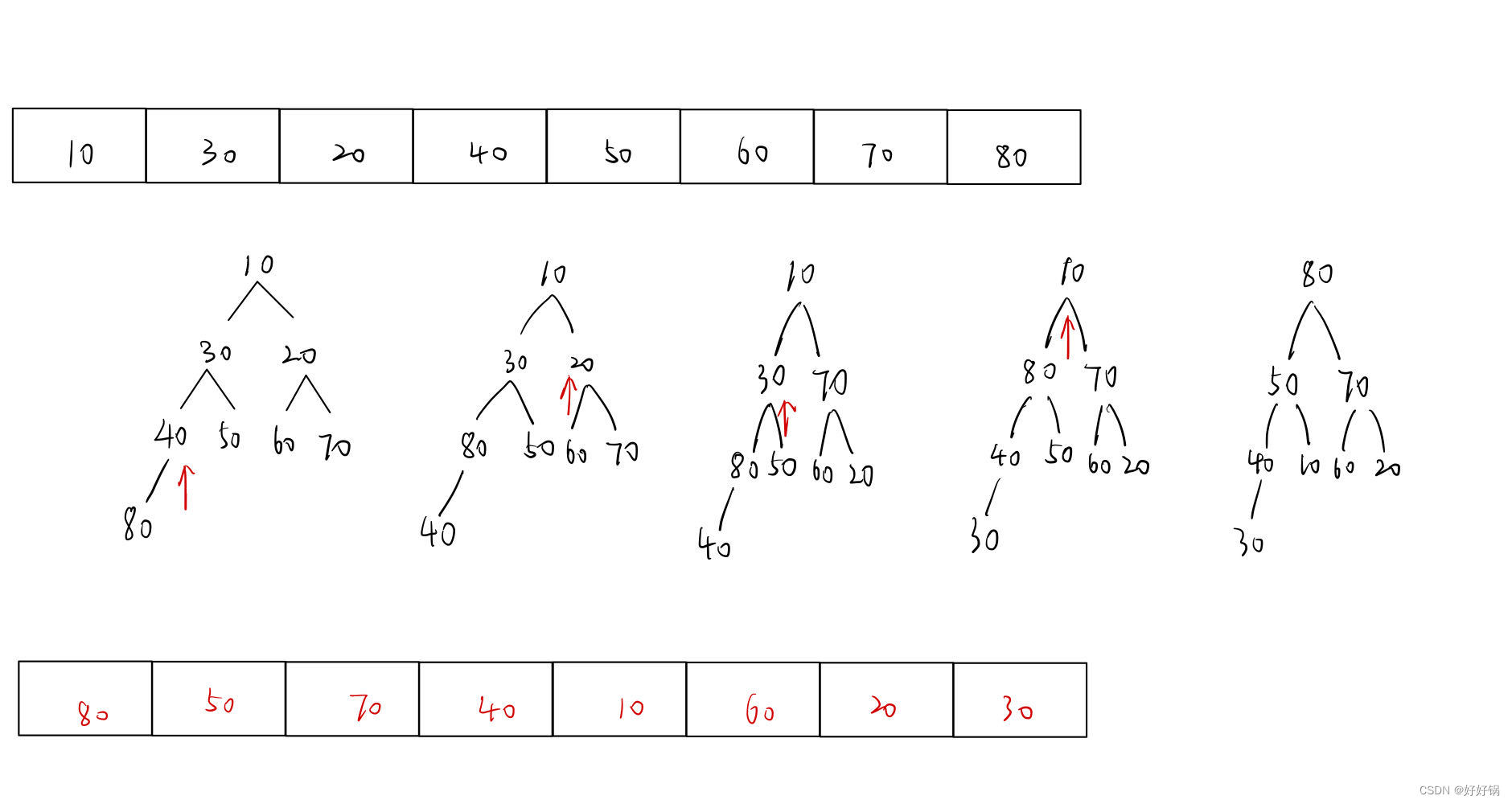
第九章:C语言数据结构与算法初阶之堆
系列文章目录 文章目录系列文章目录前言一、堆的定义二、堆的实现三、堆的接口函数1、初始化2、销毁3、插入4、删除5、判空6、元素个数四、堆排序1、建堆2、排序五、堆的应用——TOPK1、什么是TOPK问题?2、解决方法总结前言 堆就是完全二叉树。 一、堆的定义 我们…...
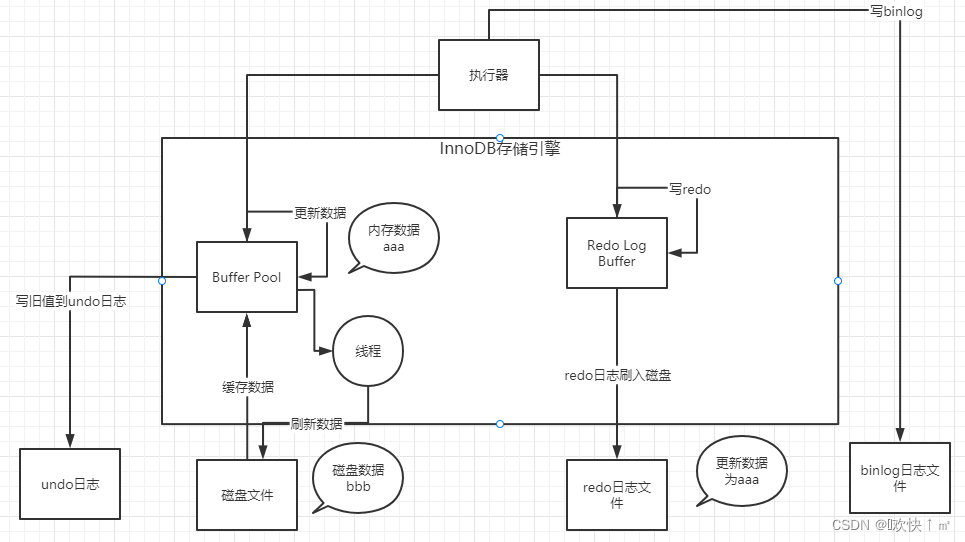
Mysql架构初识
🥲 🥸 🤌 🫀 🫁 🥷 🐻❄️🦤 🪶 🦭 🪲 🪳 🪰 🪱 🪴 🫐 🫒 🫑…...

字符串函数和内存函数
🍕博客主页:️自信不孤单 🍬文章专栏:C语言 🍚代码仓库:破浪晓梦 🍭欢迎关注:欢迎大家点赞收藏关注 字符串函数和内存函数 文章目录字符串函数和内存函数前言1. 字符串函数介绍1.1 s…...

Web3中文|GPT-4超越GPT-3.5的五大看点
A Beautiful CinderellaDwelling EagerlyFinally Gains HappinessInspiring Jealous KinLove Magically Nurtures Opulent PrinceQuietly RescuesSlipper TriumphsUniting Very WondrouslyXenial Youth Zealously这是一段描述童话故事《灰姑娘》的内容,它出自GPT-4之…...
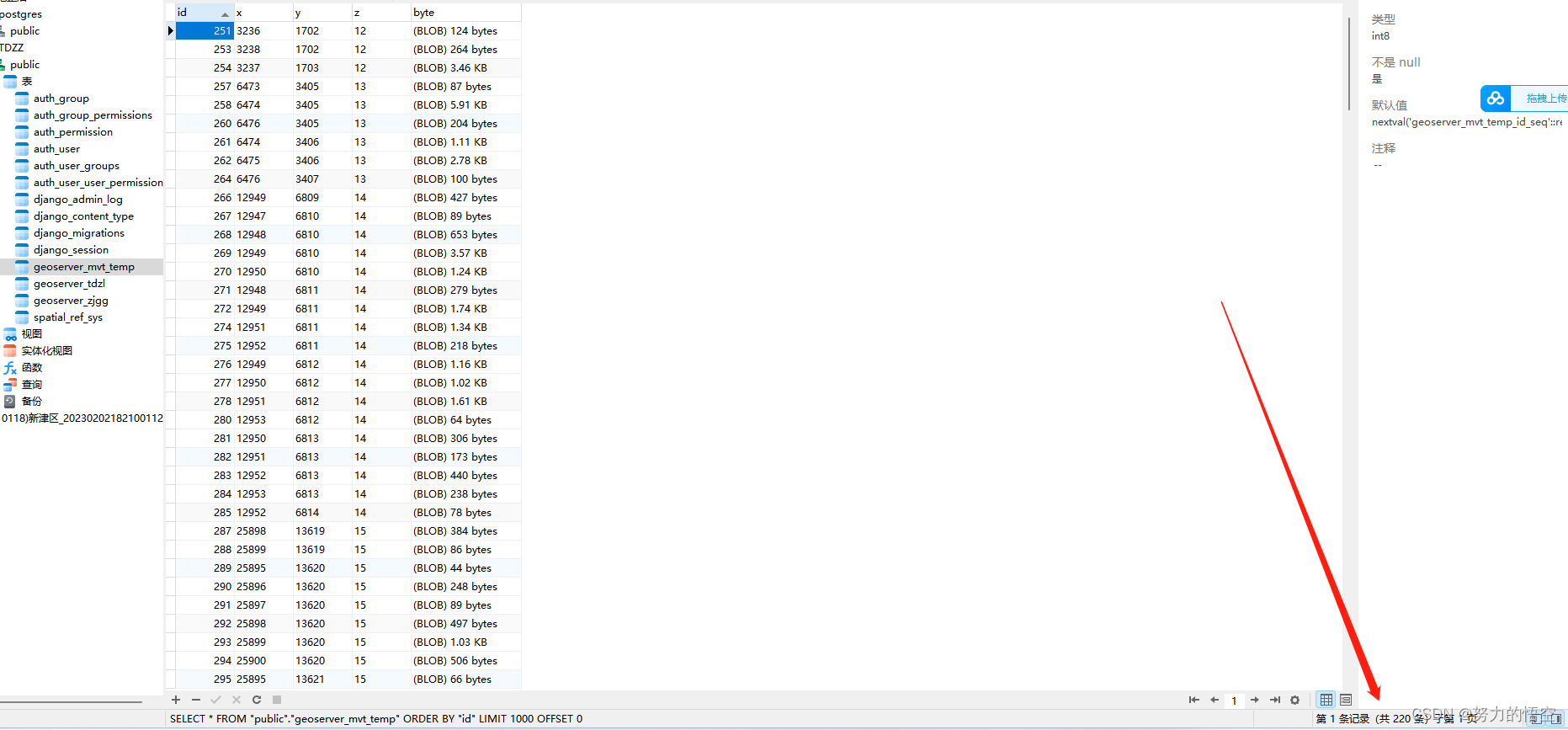
动态矢量瓦片缓存库方案
目录 前言 二、实现步骤 1.将数据写入postgis数据库 2.将矢量瓦片数据写入缓存库 3.瓦片接口实现 4.瓦片局部更新接口实现 总结 前言 矢量瓦片作为webgis目前最优秀的数据格式,其主要特点就是解决了大批量数据在前端渲染时出现加载缓慢、卡顿的问题࿰…...

628.三个数的最大乘积
给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。 示例 1: 输入:nums [1,2,3] 输出:6 示例 2: 输入:nums [1,2,3,4] 输出:24 示例 3: …...

【数据结构】堆和集合笔记
自己写一个堆首先,明确一下,为什么需要堆?>考虑插入,删除,查找的效率。数组,查找,最快是二分查找O(lgN)。但查找完如果要做什么操作,比如删除,就要挪动元素了。所以合…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
