第九章:C语言数据结构与算法初阶之堆
系列文章目录
文章目录
- 系列文章目录
- 前言
- 一、堆的定义
- 二、堆的实现
- 三、堆的接口函数
- 1、初始化
- 2、销毁
- 3、插入
- 4、删除
- 5、判空
- 6、元素个数
- 四、堆排序
- 1、建堆
- 2、排序
- 五、堆的应用——TOPK
- 1、什么是TOPK问题?
- 2、解决方法
- 总结
前言
堆就是完全二叉树。
一、堆的定义
我们了解到了树、二叉树等相关的概念,那么今天所讲解的堆就是基于二叉树中的完全二叉树实现的。那么在完全二叉树的基础上,堆还满足该性质:堆中的子节点始终小于等于(大于等于)父节点。
倘若,堆的父节点始终小于等于其子节点,我们就称之为小根堆。
倘若,堆的父节点始终大于等于其子节点,我们就称之为大根堆。
堆的逻辑结构与物理结构:
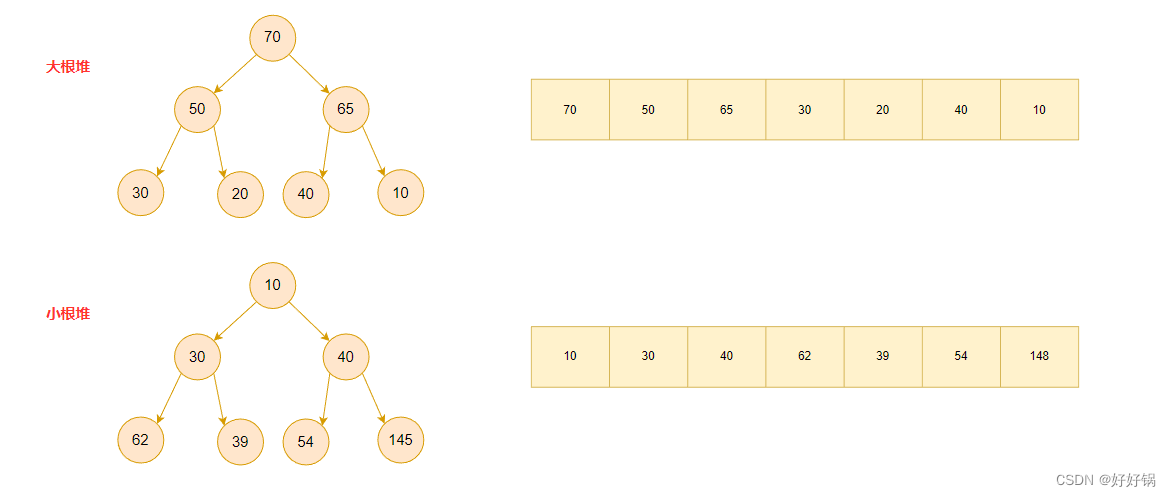
从上述的物理结构我们可以知道,我们接下来的代码实现是基于数组的。因此,我们将采用动态顺序表的思路来存储堆。
二、堆的实现
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
三、堆的接口函数
1、初始化
void HeapInit(HP* php)
{assert(php);php->size = 0;php->capacity = 4;HPDataType* cur = (HPDataType*)malloc(sizeof(HP));assert(cur);php->a = cur;
}
2、销毁
void HeapDestory(HP* php)
{assert(php);php->size = 0;php->capacity = 0;free(php->a);php->a = NULL;
}
3、插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if(php->capacity == php->size){//扩容php->capacity *= 2;HPDataType* cur = (HPDataType*)realloc(php->a, sizeof(HP) * php->capacity);assert(cur);php->a = cur;}php->a[php->size++] = x;AdjustUp(php->a, php->size - 1);}
我们是在最后一个位置插入一个数据,然后再让这个数据向上移动。
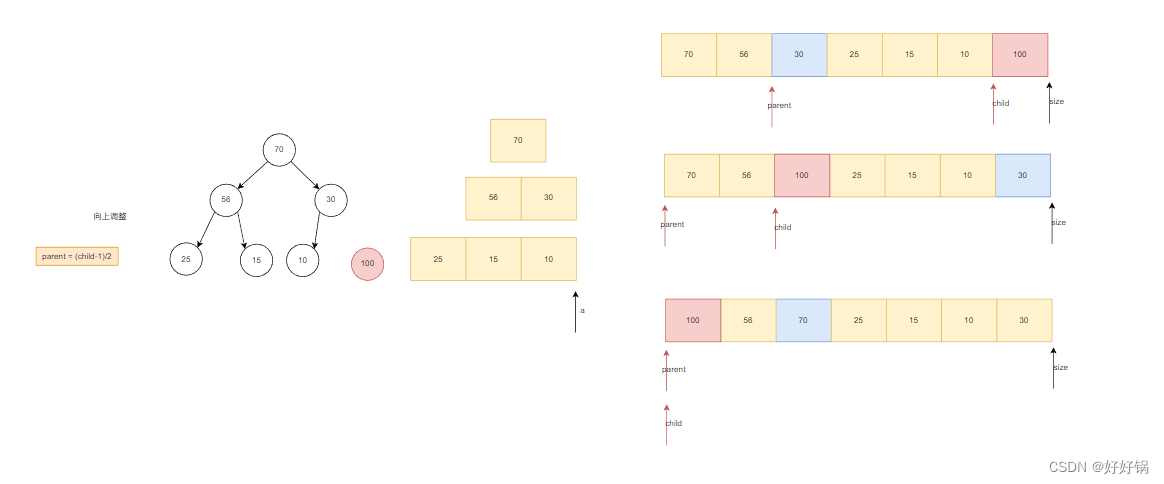
我们发现,100需要向上移动的话,只需要和100的祖宗们相比较。因此,我们可以写出AdjustUp的函数。
void AdjustUp(HPDataType* a, int child)
{//向上调整int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child]){swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
4、删除
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);swap(&php->a[0], &php->a[--php->size]);AdjustDown(php->a, 0, php->size);
}
我们这里需要删除的是堆顶。但数组中删除堆顶元素的时间复杂度是O(N)。这是相当复杂的,而尾删的时间复杂度是O(1),于是我们这里也是先将尾部元素和堆顶元素进行交换,然后再将堆顶元素向下移动。
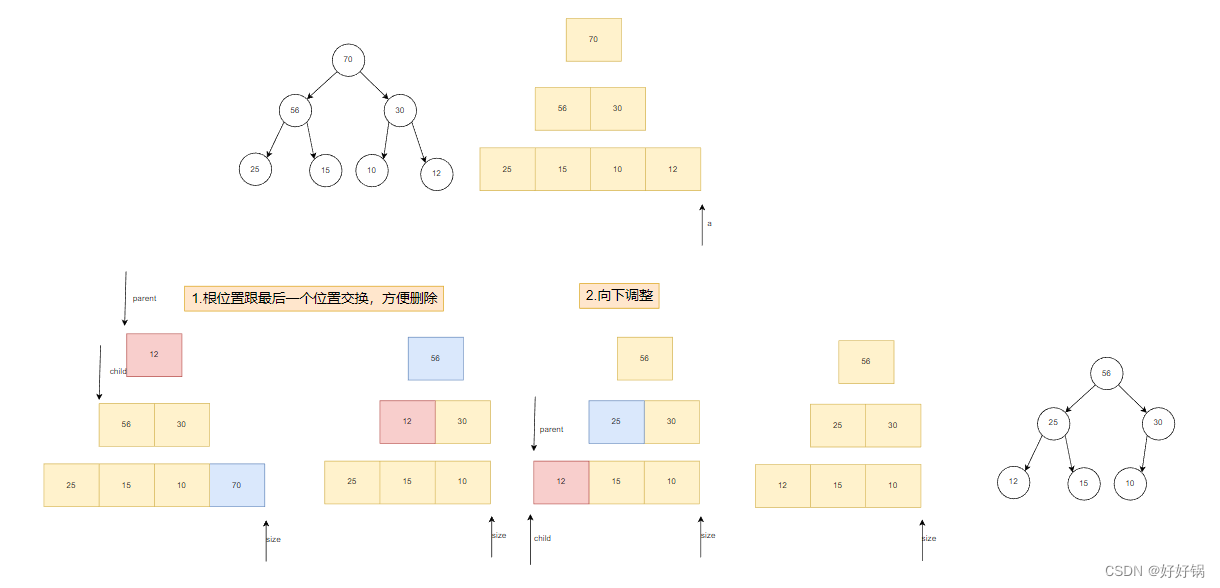
void AdjustDown(HPDataType* a, int parent, int size)
{//向下调整int child = parent * 2 + 1;while (child < size){//确认child指向大的哪个孩子if (child + 1 < size && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){//孩子大于父亲,交换,继续向下调整swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{//孩子小于父亲break;}}
}
5、判空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
6、元素个数
int HeapSize(HP* php)
{assert(php);return php->size;
}
四、堆排序
1、建堆
堆排序的基础是将数组中的元素建成一个堆:
方式1:尾插
我们从第一个元素开始,不断地插入新元素,然后让这个元素向上调整,让其对应到相应的位置。让数组始终保持一个堆,这样才能向上调整。
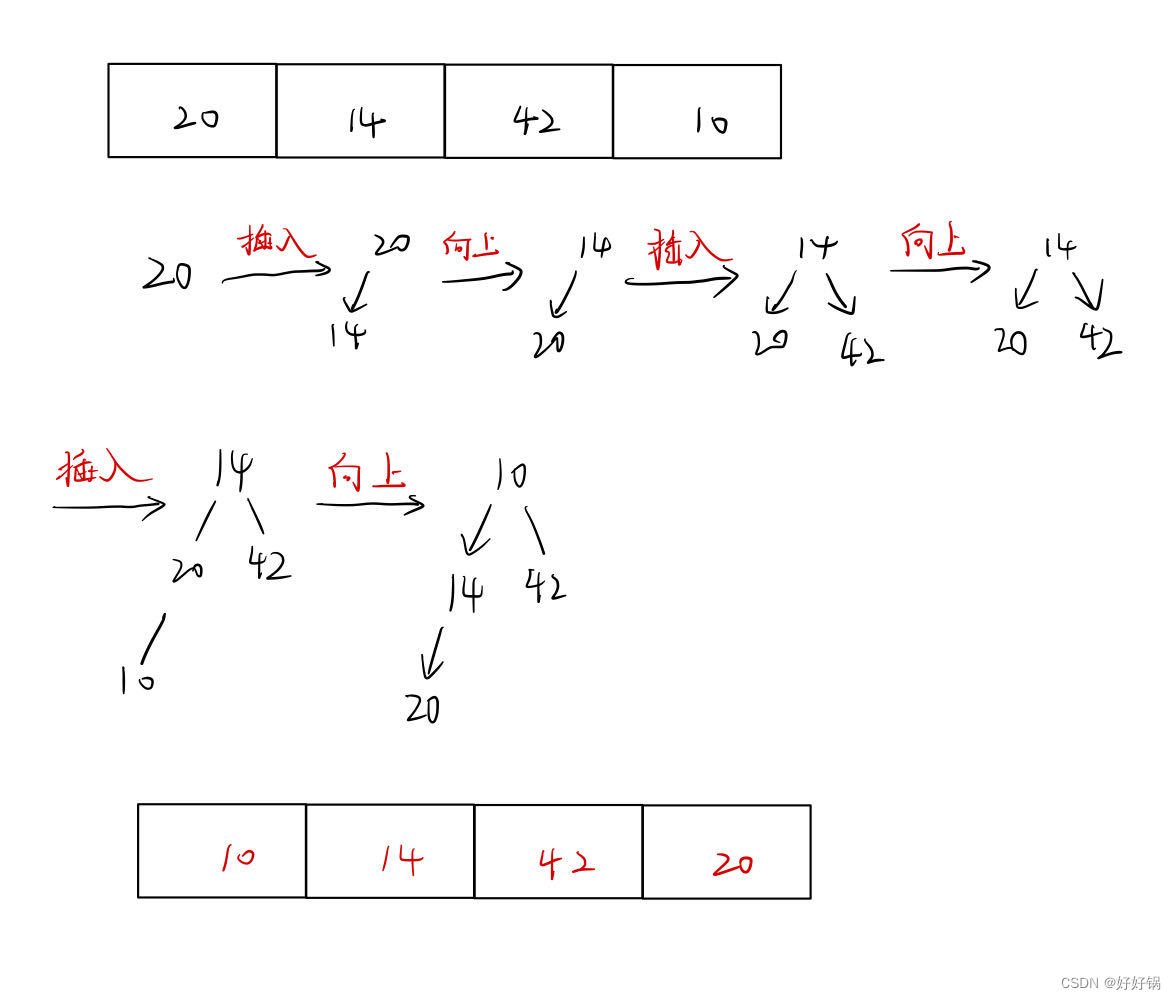
void AdjustUp(int*arr,int child)
{int parent=(child-1)>>1;while(child>0){if(arr[child]>arr[parent]){swap(arr[child],arr[parent]);child=parent;parent=(child-1)>>1;}else break;}
}
void Heap_Sort(int*arr,int size)
{//建堆for(int i=0;i<size;i++){AdjustUp(arr,i);}//.....
}
方式2:根节点向下调整
向下调整一般是针对根节点的,但是向下调整要保证下面紧跟的两个子树是两个堆,否则就会出错。因此,我们可以从倒数第二排开始,不断调整每一个小堆,从小到大,从少到多。
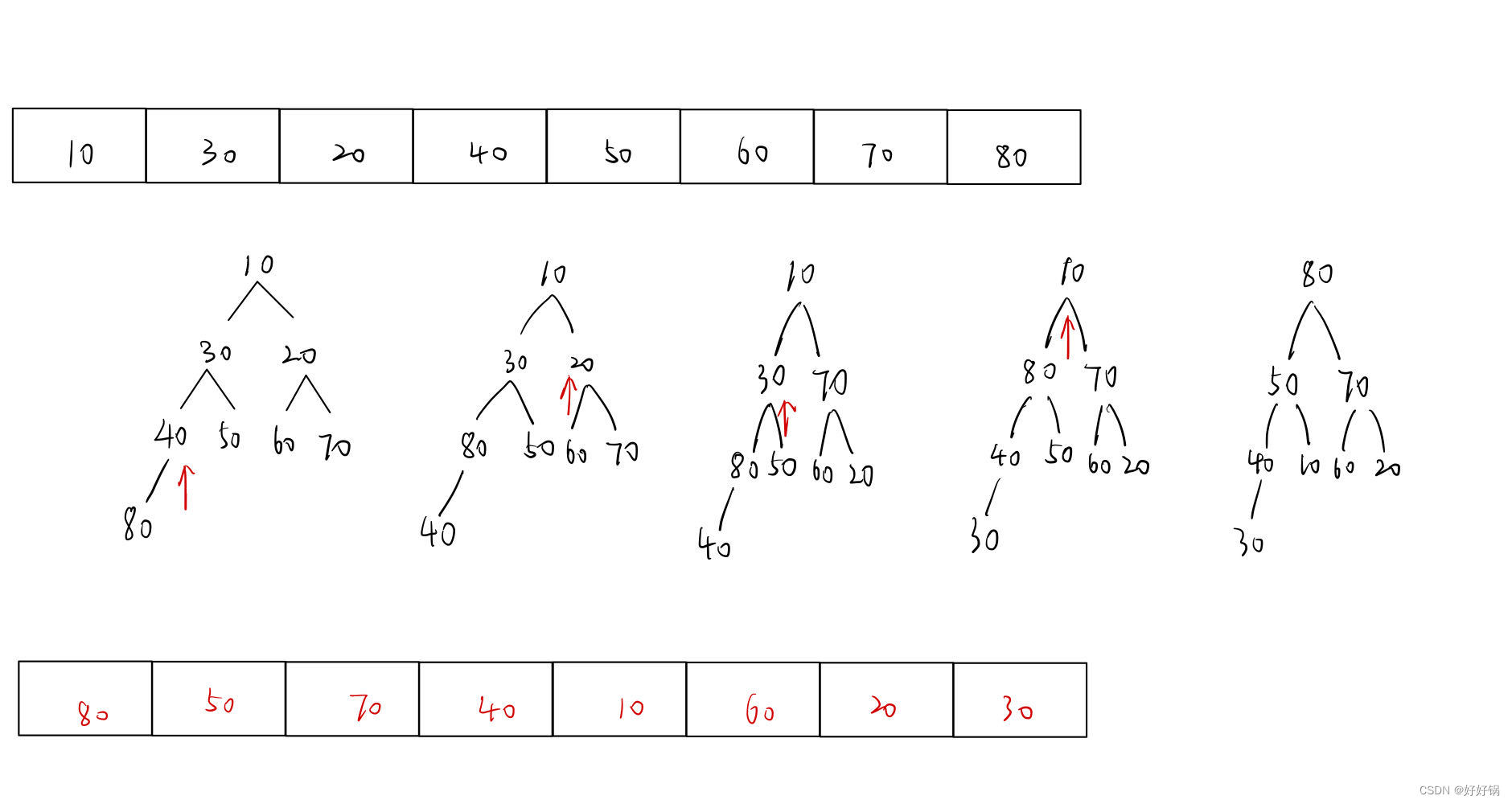
我们先保证两个子树是堆,然后再去调整这个两个子树的根节点。
void AdjustDown(int*arr,int size,int parent)
{int child=parent*2+1;while(child<size){if(child+1<size&&arr[child+1]>arr[child])child++;if(arr[child]>arr[parent]){swap(arr[child],arr[parent]);parent=child;child=parent*2+1;}else break;}
}
void Heap_Sort(int*arr,int size)
{//搭建一个大根堆for(int i=(size-1-1)/2;i>=0;i--){AdjustDown(arr,size,i);}//.........
}
2、排序
排序的话,假设我们是升序排列,但是我们创建的小根堆,那么每次取出根节点,但是取出之后,我们的堆的结构就混乱了,因此我们就需要重新建堆,此时的时间复杂度是n方。
于是我们换一个思路,我们创建一个大根堆,那么根节点就是最大的,我们让根节点和最后一个元素交换,然后我们删掉最后一个元素,即让尾指针前移,此时我们的最大值存储在了数组中的最后一位,然后我们让根节点向下移动,恢复堆的结构,此时堆顶就是次大值,然后我们再交换,让次大的元素到倒数第二的位置。由此类推,最后就能排好所有元素,其顺序为升序。
我们的根节点向下移动的时间复杂度是O(logN),共N个元素,此时时间复杂度是O(NlogN)。
#include<iostream>
#include<ctime>
using namespace std;
void AdjustDown(int*arr,int size,int parent)
{int child=parent*2+1;while(child<size){if(child+1<size&&arr[child+1]>arr[child])child++;if(arr[child]>arr[parent]){swap(arr[child],arr[parent]);parent=child;child=parent*2+1;}else break;}
}
void Heap_Sort(int*arr,int size)
{for(int i=(size-1-1)/2;i>=0;i--){AdjustDown(arr,size,i);}for(int end=size-1;end>0;end--){swap(arr[0],arr[end]);AdjustDown(arr,end,0);}
}
五、堆的应用——TOPK
1、什么是TOPK问题?
topk问题就是,我们再一堆数字中选出前K个最大的或者最小的数字。
2、解决方法
如果我们的数据量是十个亿,此时我们的内存区是不支持将其造成一个堆的,所以我们利用前k个元素创建一个元素个数为k的小根堆,那么我们堆中的较大元素一定会 “沉底”。此时,我们再去不断地读取元素,然后让这个元素和根节点比较,如果大于根节点,我们就替换掉根节点,然后让替换后的新的根节点下沉,为什么让这二者比较呢?因为我们创建的是小根堆,但是我们想要的是最大值,而根节点是最小的,所以根节点是最有可能被换掉的,所以我们让根节点去比较,最终剩下的这个元素为K的堆,就是答案。
// 在N个数找出最大的前K个 or 在N个数找出最小的前K个
void TopK(int* a, int n, int k)
{HP hp;HeapInit(&hp);// 创建一个K个数的小堆for (int i = 0; i < k; ++i){HeapPush(&hp, a[i]);}// 剩下的N-K个数跟堆顶的数据比较,比他小,就替换他进堆for (int i = k; i < n; ++i){if (a[i] < HeapTop(&hp)){HeapPop(&hp);HeapPush(&hp, a[i]);}}HeapPrint(&hp);HeapDestroy(&hp);
}总结
堆是一个逻辑上的完全二叉树,物理上是动态顺序表。
在希望与失望的决斗中,如果你用勇气与坚决的双手紧握着,胜利必属于希望。——普里尼
相关文章:

第九章:C语言数据结构与算法初阶之堆
系列文章目录 文章目录系列文章目录前言一、堆的定义二、堆的实现三、堆的接口函数1、初始化2、销毁3、插入4、删除5、判空6、元素个数四、堆排序1、建堆2、排序五、堆的应用——TOPK1、什么是TOPK问题?2、解决方法总结前言 堆就是完全二叉树。 一、堆的定义 我们…...
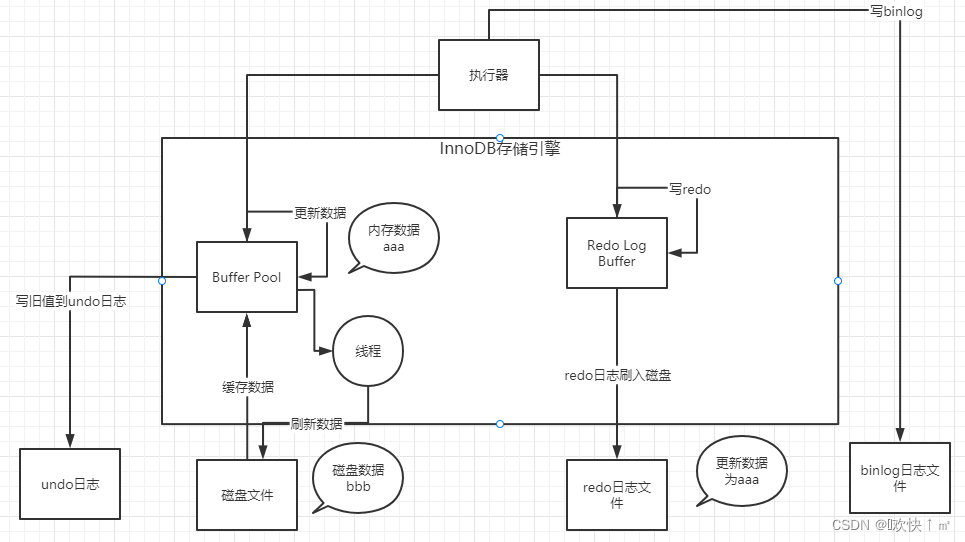
Mysql架构初识
🥲 🥸 🤌 🫀 🫁 🥷 🐻❄️🦤 🪶 🦭 🪲 🪳 🪰 🪱 🪴 🫐 🫒 🫑…...

字符串函数和内存函数
🍕博客主页:️自信不孤单 🍬文章专栏:C语言 🍚代码仓库:破浪晓梦 🍭欢迎关注:欢迎大家点赞收藏关注 字符串函数和内存函数 文章目录字符串函数和内存函数前言1. 字符串函数介绍1.1 s…...

Web3中文|GPT-4超越GPT-3.5的五大看点
A Beautiful CinderellaDwelling EagerlyFinally Gains HappinessInspiring Jealous KinLove Magically Nurtures Opulent PrinceQuietly RescuesSlipper TriumphsUniting Very WondrouslyXenial Youth Zealously这是一段描述童话故事《灰姑娘》的内容,它出自GPT-4之…...
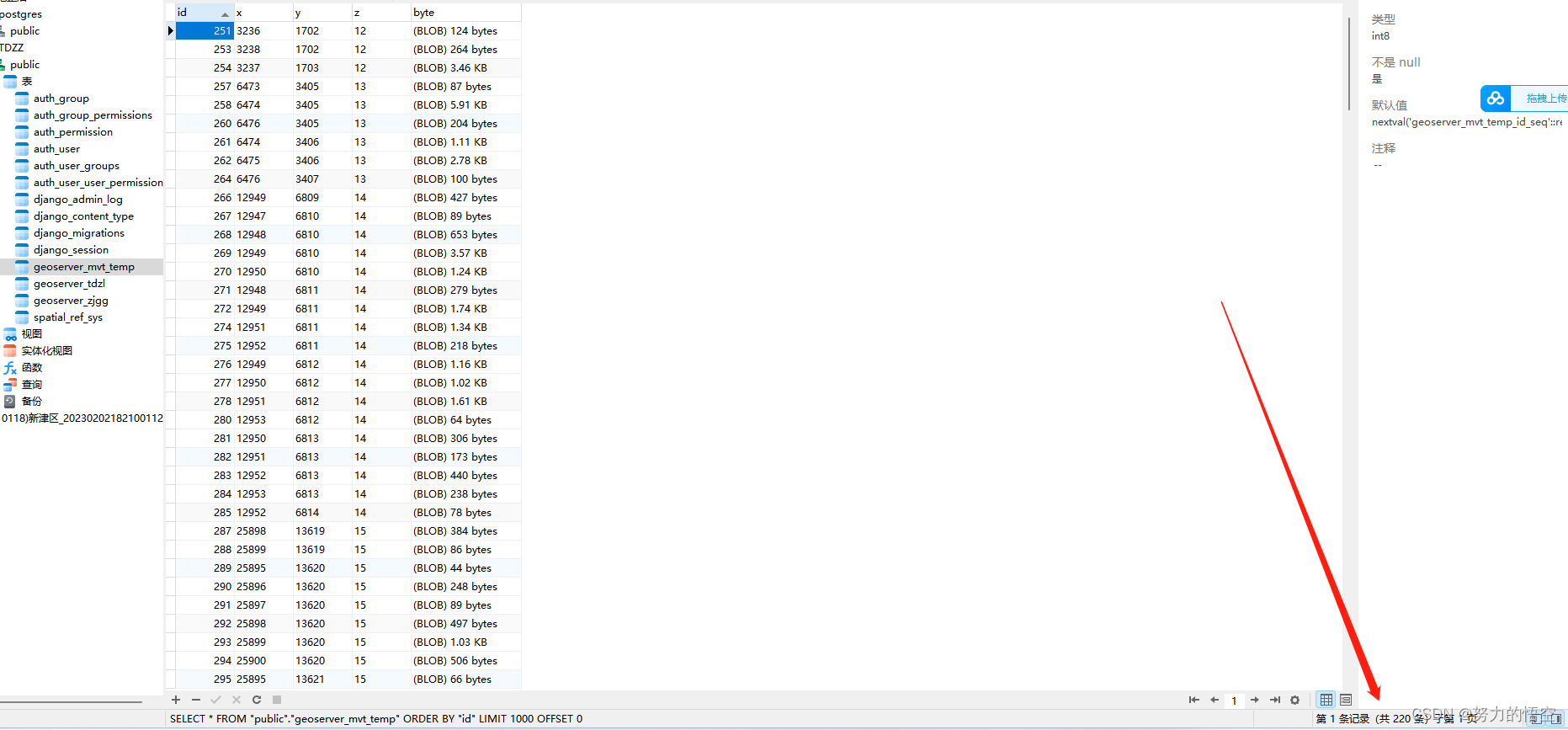
动态矢量瓦片缓存库方案
目录 前言 二、实现步骤 1.将数据写入postgis数据库 2.将矢量瓦片数据写入缓存库 3.瓦片接口实现 4.瓦片局部更新接口实现 总结 前言 矢量瓦片作为webgis目前最优秀的数据格式,其主要特点就是解决了大批量数据在前端渲染时出现加载缓慢、卡顿的问题࿰…...

628.三个数的最大乘积
给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。 示例 1: 输入:nums [1,2,3] 输出:6 示例 2: 输入:nums [1,2,3,4] 输出:24 示例 3: …...

【数据结构】堆和集合笔记
自己写一个堆首先,明确一下,为什么需要堆?>考虑插入,删除,查找的效率。数组,查找,最快是二分查找O(lgN)。但查找完如果要做什么操作,比如删除,就要挪动元素了。所以合…...
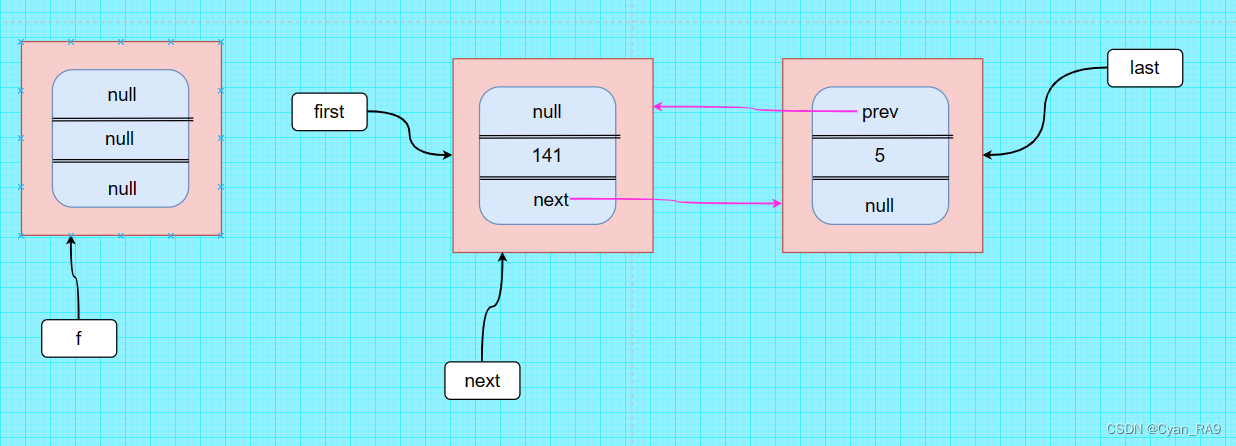
java LinkedList 源码分析(通俗易懂)
目录 一、前言 二、LinkedList类简介 三、LinkedList类的底层实现 四、LinkedList类的源码解读 1.add方法解读 : 〇准备工作 。 ①跳入无参构造。 ②跳入add方法。 ③跳入linkList方法。 ④增加第一个元素成功。 ⑤向链表中添加第二个元素。 2.remove方法解读 : 〇准备工…...

Vue中实现路由跳转的三种方式详细分解
vue中实现路由跳转的三种方式 目录 vue中实现路由跳转的三种方式 一、使用vue-router 1.下载vue-router模块到当前工程 2.在main.js中引入VueRouter函数 3.添加到Vue.use()身上 – 注册全局RouterLink和RouterView组件 4.创建路由规则数组 – 路径和组件名对应关系 5…...

全国自学考试03708《中国近现代史纲要》重点复习精要
1. 西方列强的殖民扩张和鸦片战争的影响。(两面性) :反面—破坏了了中国的小农经济,是中国由封建社会转变为两半社会。 --一系列不公平条约,破坏了中国主权领土完整。 --压迫中国人民,给中国人民带来了巨大…...

数据库面试题——锁
了解数据库的锁吗? 锁是数据库系统区别于文件系统的一个关键特性,锁机制用于管理对共享资源的并发访问。 InnoDB下两种标准行级锁: 共享锁(S Lock),允许事务读一行数据。 排他锁(X Lock&…...

Python笔记 -- 文件和异常
文章目录1、文件1.1、with关键字1.2、逐行读取1.3、写入模式1.4、多行写入2、异常2.1、try-except-else2.2、pass1、文件 1.1、with关键字 with关键字用于自动管理资源 使用with可以让python在合适的时候释放资源 python会将文本解读为字符串 # -*- encoding:utf-8 -*- # 如…...

蓝桥杯刷题冲刺 | 倒计时24天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.修剪灌木2.统计子矩阵1.修剪灌木 题目 链接: 修剪灌木 - 蓝桥云课 (lanqiao.cn) 找…...
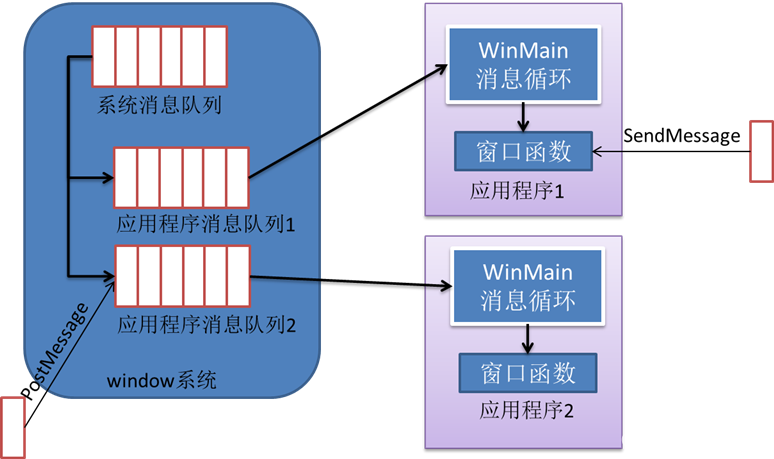
真正理解微软Windows程序运行机制——什么是消息
我是荔园微风,作为一名在IT界整整25年的老兵,今天说说Windows程序的运行机制。经常被问到MFC到底是一个什么技术,为了解释这个我之前还写过帖子,但是很多人还是不理解。其实这没什么,我在学生时代也被这个问题困绕过。…...
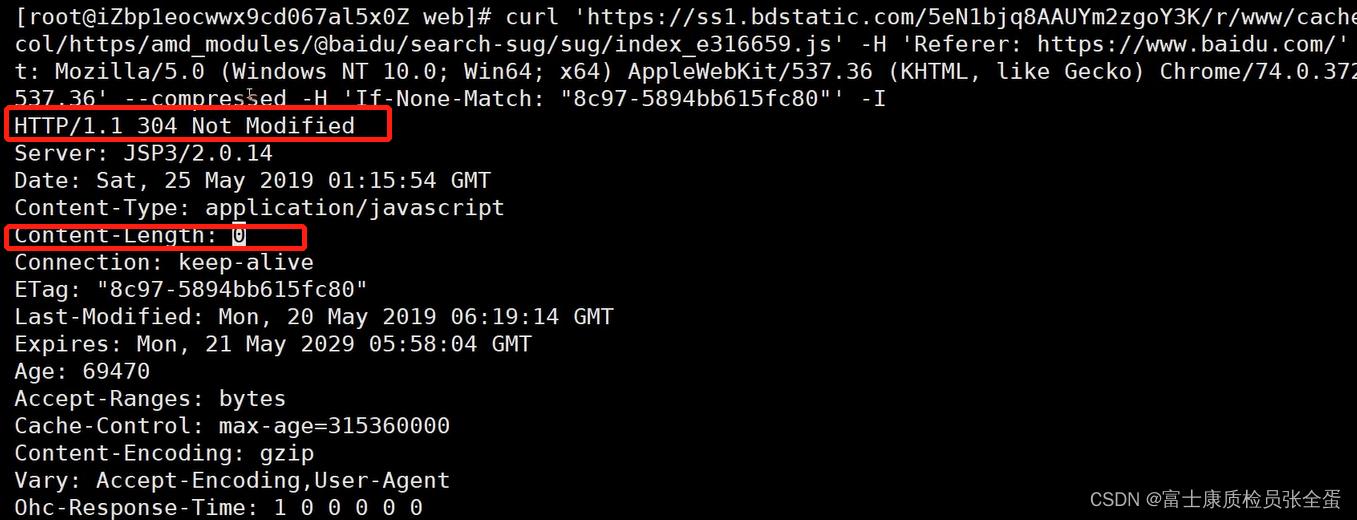
HTTP 缓存的工作原理
缓存是解决http1.1当中的性能问题主要手段。缓存可能存在于客户端浏览器上,也可以存在服务器上面,当使用过期缓存可能给用户展示的是错误的信息而导致一些bug。 HTTP 缓存:为当前请求复用前请求的响应 • 目标:减少时延࿱…...
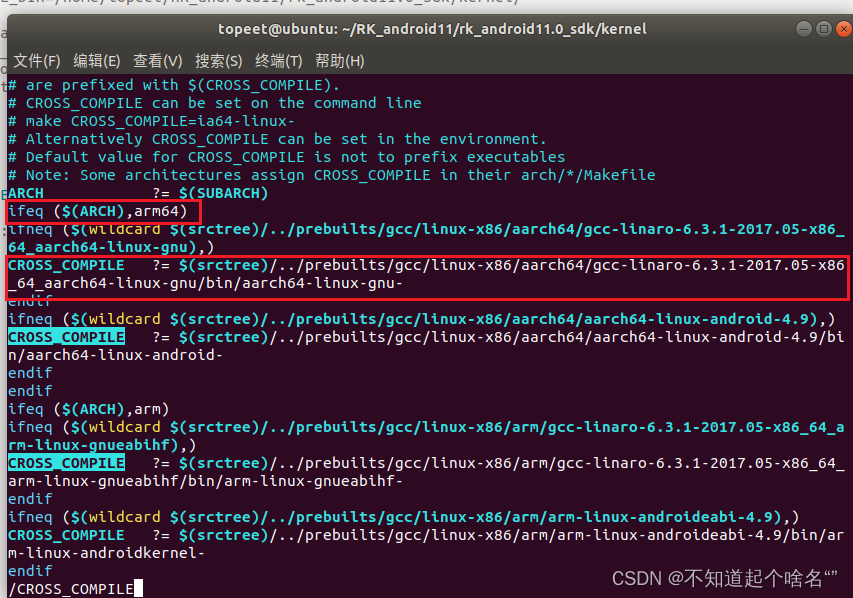
RK3568在Android上进行驱动模块开发(源码外)
文章目录 前言一、ARCH架构二、编译器三、建立自己的Makefile文件总结前言 本文记录在驱动开发时,由于编译内核时间较长,经常会选择单独编译一个模块,这里主要讲解,makefile文件如何编写(主要是编译器和架构) 提示:以下是本篇文章正文内容,下面案例可供参考 一、ARCH…...

操作技巧 | 在Revit中借用CAD填充图案的方法
在建模过程中,有时需要达到多种填充效果,而CAD中大量的二维填充图案,便是最直接的资源之一。 使用 填充图案之前 使用 填充图案之后 其中要用到主要命令便是对表面填充图案的添加与编辑 简单效果 如下 模型填充与绘图填充 区别 模型填…...
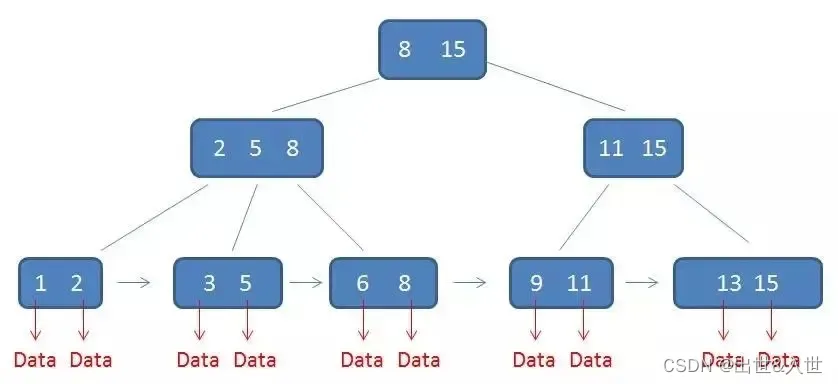
Java的二叉树、红黑树、B+树
数组和链表是常用的数据结构,数组虽然查找快(有序数组可以通过二分法查找),但是插入和删除是比较慢的;而链表,插入和删除很快(只需要改变一些引用值),但是查找就很慢&…...

昨天某读者拿到华为OD岗位offer,今天来分享一下经验,包含华为OD机试
来自读者投稿,已经拿到华为 OD 开发岗位 offer,询问了一些问题,下面是他的一些经验。 文章目录华为 OD 投递简历华为 OD 机试分数OD 机试通过之后,收到综合测评OD 技术面(时长 1 小时左右)主管/HR 面试&…...
树的遍历方式(前中后,层序遍历,递归,迭代,Morris遍历)-----直接查询代码
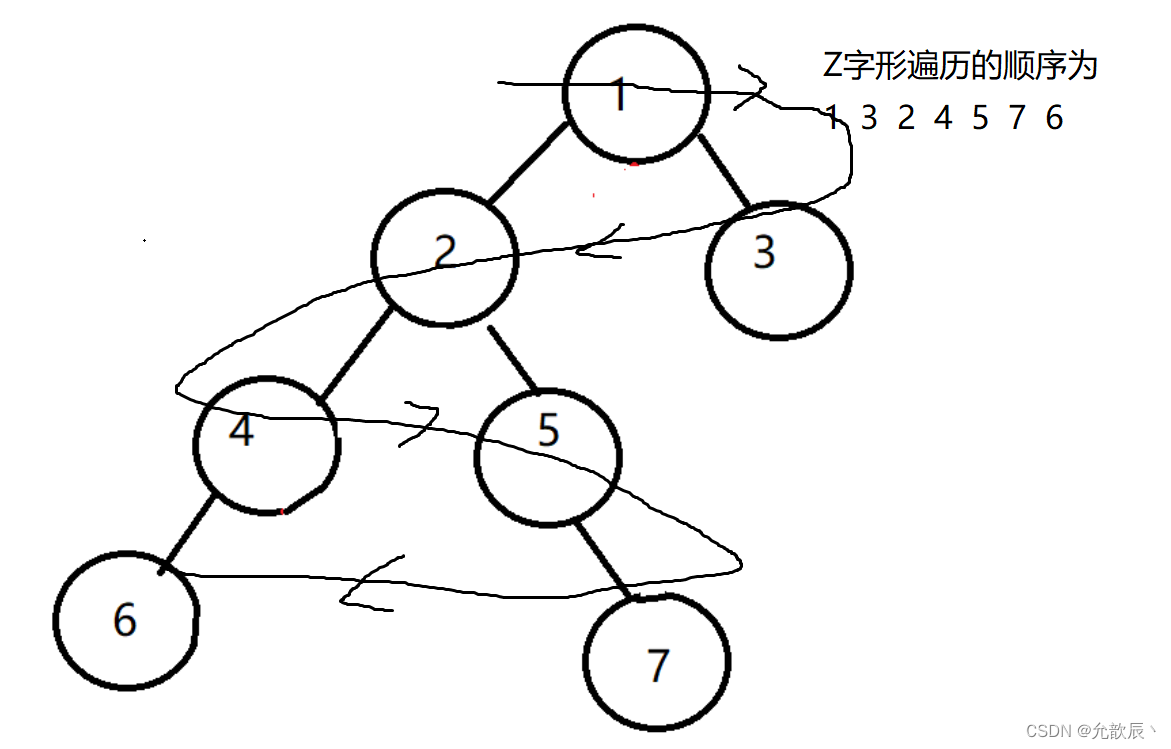
目录 一.前序遍历 1.递归 2.栈迭代 3.Morris遍历 二.中序遍历 1.递归 2.栈迭代 3.Morris遍历 三.后序遍历 1.递归 2.栈迭代 3.Morris遍历 四.前中后序的统一迭代法 1.前序遍历 2.中序遍历 3.后序遍历 五.层序遍历 1.队列迭代 2.之字形层序遍历 3.锯齿形层序…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
