(C++二叉树02) 翻转二叉树 对称二叉树 二叉树的深度
226、翻转二叉树
递归法:
交换两个结点可以用swap()方法
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if(root == NULL) return NULL;TreeNode* tem = root->left;root->left = root->right;root->right = tem;invertTree(root->left);invertTree(root->right);return root;}
};迭代法:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if(root == NULL) return NULL;stack<TreeNode*> sta;sta.push(root);while(!sta.empty()) {TreeNode* tem= sta.top();sta.pop();swap(tem->left, tem->right);if(tem->right) sta.push(tem->right);if(tem->left) sta.push(tem->left);}return root;}
};101、对称二叉树
递归法:
class Solution {
public:bool compare(TreeNode* left, TreeNode* right) {if(left == NULL && right != NULL) {return false;}else if(left != NULL && right == NULL) {return false;}else if(left == NULL && right == NULL){return true;}else if (left->val != right->val) {return false;}return compare(left->left, right->right) && compare(left->right, right->left);}bool isSymmetric(TreeNode* root) {if(root == NULL) return true;return compare(root->left, root->right);}
};104、二叉树的最大深度
递归法:
class Solution {
public:int depth(TreeNode* root) {if(root == NULL) return 0;int left = depth(root->left);int right = depth(root->right);return left > right ? left + 1 : right + 1;}int maxDepth(TreeNode* root) {if(root == NULL) return 0;return depth(root);}
};迭代法:
class Solution {
public:int maxDepth(TreeNode* root) {if(root == NULL) return 0;queue<TreeNode*> que;int depth = 0;que.push(root);while(!que.empty()) {int size = que.size();depth++;for(int i = 0; i < size; i++) {TreeNode* tem = que.front();que.pop();if(tem->left) que.push(tem->left);if(tem->right) que.push(tem->right);}}return depth;}
};111、二叉树的最小深度
递归法:
class Solution {
public:int depth(TreeNode* root) {if(root->left == NULL && root->right == NULL) {return 1;}else if(root->left != NULL && root->right == NULL) {return depth(root->left) + 1;}else if(root->left == NULL && root->right != NULL) {return depth(root->right) + 1;}int left = depth(root->left);int right = depth(root->right);return left > right ? right + 1 : left + 1;}int minDepth(TreeNode* root) {if(root == NULL) return 0;return depth(root);}
};迭代法:
class Solution {
public:int minDepth(TreeNode* root) {if(root == NULL) return 0;queue<TreeNode*> que;int depth = 0;que.push(root);while(!que.empty()) {int size = que.size();depth++;for(int i = 0; i < size; i++) {TreeNode* tem = que.front();que.pop();if(tem->left == NULL && tem->right == NULL) {return depth;}if(tem->left) que.push(tem->left);if(tem->right) que.push(tem->right);}}return depth;}
};相关文章:
 翻转二叉树 对称二叉树 二叉树的深度)
(C++二叉树02) 翻转二叉树 对称二叉树 二叉树的深度
226、翻转二叉树 递归法: 交换两个结点可以用swap()方法 class Solution { public:TreeNode* invertTree(TreeNode* root) {if(root NULL) return NULL;TreeNode* tem root->left;root->left root->right;root->right tem;invertTree(root->l…...

高阶面试-mongodb
mongodb的特点,为什么使用他 nosql数据库,前端到后端到数据库,都是json,无模式,数据模型发生变更,不需要强制更新表结构,可以快速实现需求迭代。 天生分布式,高可用,处…...

MySQL数据库慢查询日志、SQL分析、数据库诊断
1 数据库调优维度 业务需求:勇敢地对不合理的需求说不系统架构:做架构设计的时候,应充分考虑业务的实际情况,考虑好数据库的各种选择(读写分离?高可用?实例个数?分库分表?用什么数据库?)SQL及索引:根据需求编写良…...

[短笔记] Ubuntu配置环境变量的最佳实践
结论: 不确定是否要设为系统,则先针对当前用户设,写~/.profile确定为系统级,写/etc/environment,注意无需export不推荐写在~/.bashrc(Ubuntu不推荐,理由见references) References&…...

怎样在 PostgreSQL 中优化对多表关联的连接条件选择?
🍅关注博主🎗️ 带你畅游技术世界,不错过每一次成长机会!📚领书:PostgreSQL 入门到精通.pdf 文章目录 怎样在 PostgreSQL 中优化对多表关联的连接条件选择一、理解多表关联的基本概念二、选择合适的连接条件…...
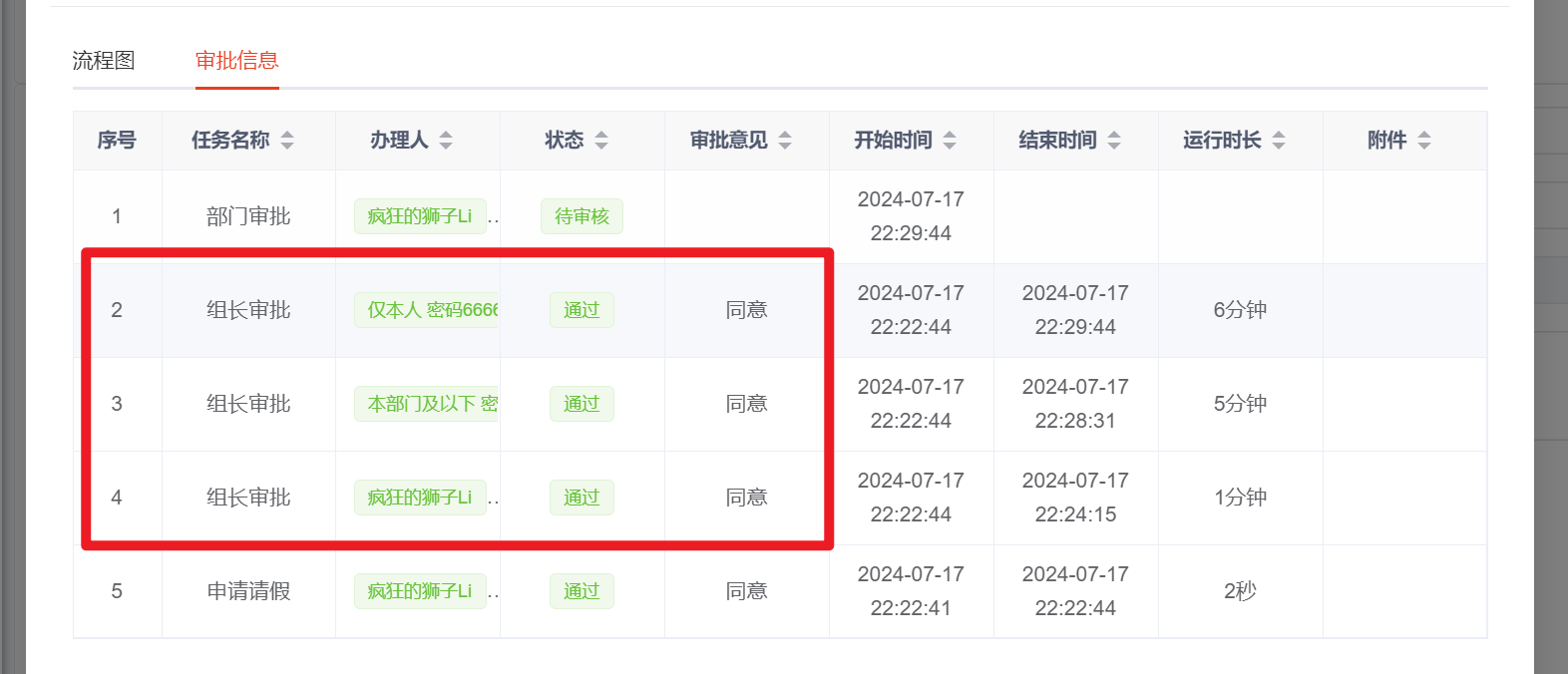
【Flowable | 第四篇】flowable工作流多任务实例节点实现会签/或签
文章目录 5.flowable工作流多任务实例节点实现会签/或签5.1会签/或签概念5.2多实例配置说明5.3会签例子5.3.1用户候选人配置5.3.2多实例配置5.3.3执行监听器配置5.3.5测试 5.flowable工作流多任务实例节点实现会签/或签 5.1会签/或签概念 我们在本篇中,将使用多任…...

解决C#读取US7ASCII字符集oracle数据库的中文乱码
👨 作者简介:大家好,我是Taro,全栈领域创作者 ✒️ 个人主页:唐璜Taro 🚀 支持我:点赞👍📝 评论 ⭐️收藏 文章目录 前言一、解决方法二、安装System.Data.OleDb连接库三…...

Linux驱动开发中设备节点、虚拟节点、逻辑节点之间的区别与关系
概述 在Linux DTS中我们可以看到各种各样的节点,每个节点都是对某一物理设备或功能抽象或具体的描述 设备节点 设备节点是对物理设备的一种具体的描述,它一般包含设备的寄存器地址、设备的类型、中断、时钟频率这些通用信息,除了这些通用信…...

【iOS】——ARC源码探究
一、ARC介绍 ARC的全称Auto Reference Counting. 也就是自动引用计数。使用MRC时开发者不得不花大量的时间在内存管理上,并且容易出现内存泄漏或者release一个已被释放的对象,导致crash。后来,Apple引入了ARC。使用ARC,开发者不再…...

ubuntu服务器安装labelimg报错记录
文章目录 报错提示查看报错原因安装报错 报错提示 按照步骤安装完labelimg后,在终端输入labelImg后,报错: (labelimg) rootinteractive59753:~# labelImg ………………Got keys from plugin meta data ("xcb") QFactoryLoader::Q…...

Transformer中Decoder的计算过程及各部分维度变化
在Transformer模型中,解码器的计算过程涉及多个步骤,主要包括自注意力机制、编码器-解码器注意力和前馈神经网络。以下是解码器的详细计算过程及数据维度变化: 1. 输入嵌入和位置编码 解码器的输入首先经过嵌入层和位置编码: I…...

QT实现滑动页面组件,多页面动态切换
这篇文章主要介绍了Qt实现界面滑动切换效果,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友可以参考下。 一、简述 一个基于Qt的动态滑动页面组件。 二、 设计思路 1、自定义StackWidget类,继承自QWidget,实现一个堆叠…...

使用Python-docx库创建Word文档
哈喽,大家好,我是木头左! 简介 Python-docx是一个用于处理Microsoft Word文档的Python库。它允许用户创建、修改和提取Word文档的内容。在本文中,将详细介绍如何使用Python-docx库创建一个新的Word文档。 安装Python-docx库 要使用Python-docx库,首先需要安装它。可以使…...

C# 设计一个可变长度的数据通信协议编码和解码代码。
设计一个可变长度的数据通信协议编码和解码代码。 要有本机ID字段,远端设备ID字段,指令类型字段,数据体字段,校验字段。其中一个要求是,每次固定收发八个字节,单个数据帧超过八个字节需要分包收发。对接收的…...

【MATLAB库函数系列】MATLAB库函数pwelch之功率谱估计的详解及实现
功率谱估计 由于实际信号通常是非定常的,我们只能假设其在10ms的时间段内是定常的,并在此基础上对短的定常信号求PSD或者能谱。 窗函数的作用就是将原始的信号分割成一段段可以计算PSD和能谱的短信号,并且保证了周期结构的连续性、避免了频谱泄漏。不同的窗函数具有不同的…...

科技出海|百分点科技智慧政务解决方案亮相非洲展会
近日,华为非洲全联接大会在南非约翰内斯堡举办,吸引政府官员行业专家、思想领袖、生态伙伴等2,000多人参会,百分点科技作为华为云生态合作伙伴,重点展示了智慧政务解决方案,发表《Enable a Smarter Government with Da…...

Prometheus 云原生 - Prometheus 数据模型、Metrics 指标类型、Exporter 相关
目录 开始 Prometheus 数据类型 简单理解 时序样本 格式 和 命名要求 Metrics 指标类型 Counter 计数器 Gauge Histogram Summary Exporter 相关 概述 Exporter 类型 Exporter 规范 开始 Prometheus 数据类型 简单理解 a)安装好 Prometheus 后会暴露…...
Qt窗口程序整理汇总
到今日为止,通过一个个案例的实验,逐步熟悉了 Qt6下 窗体界面开发的,将走过的路,再次汇总整理。 Qt Splash样式的登录窗https://blog.csdn.net/castlooo/article/details/140462768 Qt实现MDI应用程序https://blog.csdn.net/cast…...

简单实现一个本地ChatGPT web服务(langchain框架)
简单实现一个本地ChatGPT 服务,用到langchain框架,fastapi,并且本地安装了ollama。 依赖安装: pip install langchain pip install langchain_community pip install langchain-cli # langchain v0.2 2024年5月最新版本 pip install bs4 pi…...
)
Elasticsearch-多边形范围查询(8.x)
目录 一、字段设计 二、数据录入 三、查询语句 四、Java代码实现 开发版本详见:Elasticsearch-经纬度查询(8.x-半径查询)_es经纬度范围查询-CSDN博客 一、字段设计 PUT /aoi_points {"mappings": {"properties": {"location": {…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...

DriveGPT4: Interpretable End-to-end Autonomous Driving via Large Language Model
一、研究背景与创新点 (一)现有方法的局限性 当前智驾系统面临两大核心挑战:一是长尾问题,即系统在遇到新场景时可能失效,例如突发交通状况或非常规道路环境;二是可解释性问题,传统方法无法解释智驾系统的决策过程,用户难以理解车辆行为的依据。传统语言模型(如 BERT…...

网络安全问题及对策研究
摘 要 网络安全问题一直是近年来社会乃至全世界十分关注的重要性问题,网络关乎着我们的生活,政治,经济等多个方面,致力解决网络安全问题以及给出行之有效的安全策略是网络安全领域的一大目标。 本论文简述了课题的开发背景&…...
