贪心算法(2024/7/16)
1合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
思路:本题是判断重叠区间问题 先排序,让所有的相邻区间尽可能的重叠在一起,按左边界,或者右边界排序都可以.
-
排序: 首先,根据每个区间的左边界,对给定的区间集合
intervals进行升序排序。这是为了确保处理区间时,可以按顺序考虑它们的位置关系。 -
合并过程: 排序完成后,使用一个结果集合
result来存储最终合并后的区间。开始时,将排序后的第一个区间直接放入result中。 -
遍历区间: 从第二个区间开始遍历,与
result中的最后一个区间比较:- 如果当前区间与
result中的最后一个区间有重叠(即当前区间的左边界小于等于result中最后一个区间的右边界),则更新result中最后一个区间的右边界为两者的最大值,以实现合并。 - 如果当前区间与
result中的最后一个区间没有重叠,则直接将当前区间加入result。
- 如果当前区间与
代码
class Solution {
public:// 定义一个静态函数作为比较函数,用于排序static bool cmp(const vector<int>& a, const vector<int>& b) {return a[0] < b[0]; // 按照区间的左边界进行升序排序}vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> result;if (intervals.empty()) return result; // 如果区间集合为空直接返回空结果// 使用cmp函数对区间进行排序sort(intervals.begin(), intervals.end(), cmp);// 第一个区间直接放入结果集合中result.push_back(intervals[0]); for (int i = 1; i < intervals.size(); i++) {if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间// 合并区间,只需要更新结果集合中最后一个区间的右边界result.back()[1] = max(result.back()[1], intervals[i][1]); } else {result.push_back(intervals[i]); // 区间不重叠,将当前区间加入结果集合}}return result;}
};2 单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10 输出: 9
示例 2:
输入: n = 1234 输出: 1234
示例 3:
输入: n = 332 输出: 299
提示:
0 <= n <= 109
思路:
举个例子,数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
- 将整数
N转换为字符串strNum,便于按位处理。 - 从右向左遍历字符串
strNum,找到第一个出现递减的位置i,即满足strNum[i-1] > strNum[i]。 - 将第
i-1位减一,并标记flag为i,表示从这里开始需要调整。 - 将从
flag开始的所有位置的字符设为 ‘9’,以确保得到最大的单调递增数。 - 将处理后的字符串转换为整数并返回作为结果。
代码:
class Solution {
public:int monotoneIncreasingDigits(int N) {string strNum = to_string(N);// flag用来标记需要修改的位置,初始化为字符串长度,防止第二个循环在未赋值的情况下执行int flag = strNum.size();// 从倒数第二位开始向前遍历for (int i = strNum.size() - 1; i > 0; i--) {// 如果当前位大于前一位,则前一位需要减一,并更新flagif (strNum[i - 1] > strNum[i]) {flag = i; // 记录需要减一的位置strNum[i - 1]--; // 前一位减一}}// 将flag位置及之后的所有位数变为9,以获得最大的单调递增数for (int i = flag; i < strNum.size(); i++) {strNum[i] = '9';}return stoi(strNum); // 转换为整数并返回}
};3监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
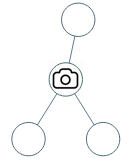
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
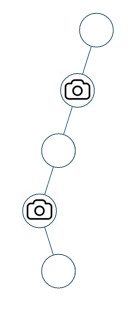
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
思路:我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!可以使用后序遍历也就是左右中的顺序,这样就可以在回溯的过程中从下到上进行推导了.
给定一个二叉树,节点状态有三种:未被覆盖、已被覆盖(无需额外摄像头)、已安装摄像头。目标是找出最少需要安装的摄像头数量,覆盖整棵树的所有节点。
定义递归函数 traversal,对当前节点进行处理:
- 如果左右子树有任意一个是未被覆盖的状态(返回2),则当前节点需要安装摄像头,返回1表示当前节点已安装摄像头。
- 如果左右子树都已被覆盖(返回0),则当前节点不需要额外的摄像头覆盖。
- 如果左右子树有一个已安装摄像头(返回1),则当前节点被覆盖,返回0。
-
根节点处理: 调用
traversal函数处理根节点。如果根节点未被覆盖(返回2),则需要额外安装一个摄像头。 -
终返回
result,即安装摄像头的总数量。
代码:
class Solution {
private:int result; // 记录需要安装摄像头的数量// 递归函数,返回当前节点的状态:// 0 - 节点已被覆盖// 1 - 节点安装了摄像头// 2 - 节点未被覆盖int traversal(TreeNode* cur) {if (cur == NULL) return 2; // 空节点默认已覆盖int left = traversal(cur->left); // 处理左子树int right = traversal(cur->right); // 处理右子树// 如果左右子树有任意一个未被覆盖,当前节点需要安装摄像头if (left == 2 || right == 2) {result++; // 安装摄像头return 1; // 当前节点已安装摄像头}// 如果左右子树的状态都是已覆盖,当前节点不需要额外摄像头覆盖else if (left == 0 && right == 0) {return 2; // 当前节点未被覆盖} else {return 0; // 当前节点已被覆盖}}public:int minCameraCover(TreeNode* root) {result = 0; // 初始化摄像头数量为0if (traversal(root) == 2) { // 如果根节点未被覆盖,则需额外安装摄像头result++;}return result; // 返回最终需要安装的摄像头数量}
};相关文章:

贪心算法(2024/7/16)
1合并区间 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 1: 输入:inter…...

Python 在Word表格中插入、删除行或列
Word文档中的表格可以用于组织和展示数据。在实际应用过程中,有时为了调整表格的结构或适应不同的数据展示需求,我们可能会需要插入、删除行或列。以下提供了几种使用Python在Word表格中插入或删除行、列的方法供参考: 文章目录 Python 在Wo…...

Java二十三种设计模式-单例模式(1/23)
引言 在软件开发中,设计模式是一套被反复使用的、大家公认的、经过分类编目的代码设计经验的总结。单例模式作为其中一种创建型模式,确保一个类只有一个实例,并提供一个全局访问点。本文将深入探讨单例模式的概念、实现方式、使用场景以及潜…...

Unity动画系统(3)---融合树
6.1 动画系统基础2-6_哔哩哔哩_bilibili Animator类 using System.Collections; using System.Collections.Generic; using UnityEngine; public class EthanController : MonoBehaviour { private Animator ani; private void Awake() { ani GetComponen…...

sqlalchemy.orm中validates对两个字段进行联合校验
版本 sqlalchemy1.4.37 需求说明 有个场景,需要在orm中对两个字段进行联合校验,当 col1 xxx’时,对 col2的长度进行检查,超过限制(500)时,进行截断。 网上找了很久,没找到类似的…...
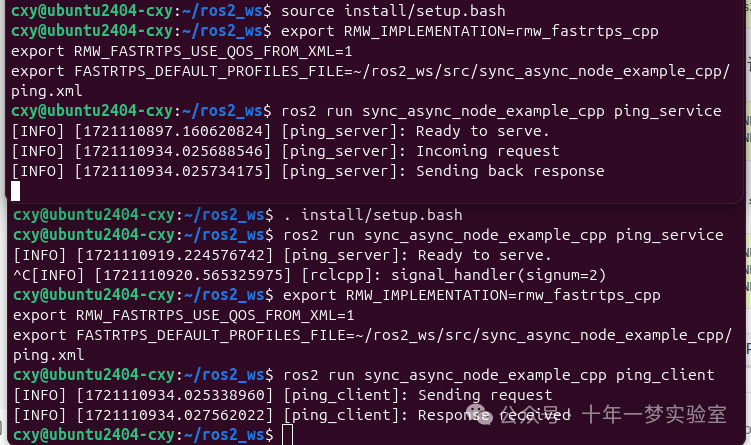
【ROS2】高级:解锁 Fast DDS 中间件的潜力 [社区贡献]
目标:本教程将展示如何在 ROS 2 中使用 Fast DDS 的扩展配置功能。 教程级别:高级 时间:20 分钟 目录 背景 先决条件在同一个节点中混合同步和异步发布 创建具有发布者的节点创建包含配置文件的 XML 文件执行发布者节点创建一个包含订阅者的节…...

VirtualBox虚拟机与主机互传文件的方法
建立共享文件夹 1.点击设置,点击共享文件夹,添加共享文件夹路径,保存 2.启动虚拟机,点击设备,点击安装增强功能,界面会出现一个光碟图标,点击光碟图标 3.打开光碟图标,出现一个目…...

访问控制系列
目录 一、基本概念 1.客体与主体 2.引用监控器与引用验证机制 3.安全策略与安全模型 4.安全内核 5.可信计算基 二、访问矩阵 三、访问控制策略 1.主体属性 2.客体属性 3.授权者组成 4.访问控制粒度 5.主体、客体状态 6.历史记录和上下文环境 7.数据内容 8.决策…...

【BUG】已解决:ModuleNotFoundError: No module named ‘cv2’
已解决:ModuleNotFoundError: No module named ‘cv2’ 欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 欢迎来到我的主页,我是博主英杰,211科班出身,就职于医疗科技公司,热衷分享知识,武汉城市开…...

成都亚恒丰创教育科技有限公司 【插画猴子:笔尖下的灵动世界】
在浩瀚的艺术海洋中,每一种创作形式都是人类情感与想象力的独特表达。而插画,作为这一广阔领域中的璀璨明珠,以其独特的视觉语言和丰富的叙事能力,构建了一个又一个令人遐想连篇的梦幻空间。成都亚恒丰创教育科技有限公司 在众多插…...
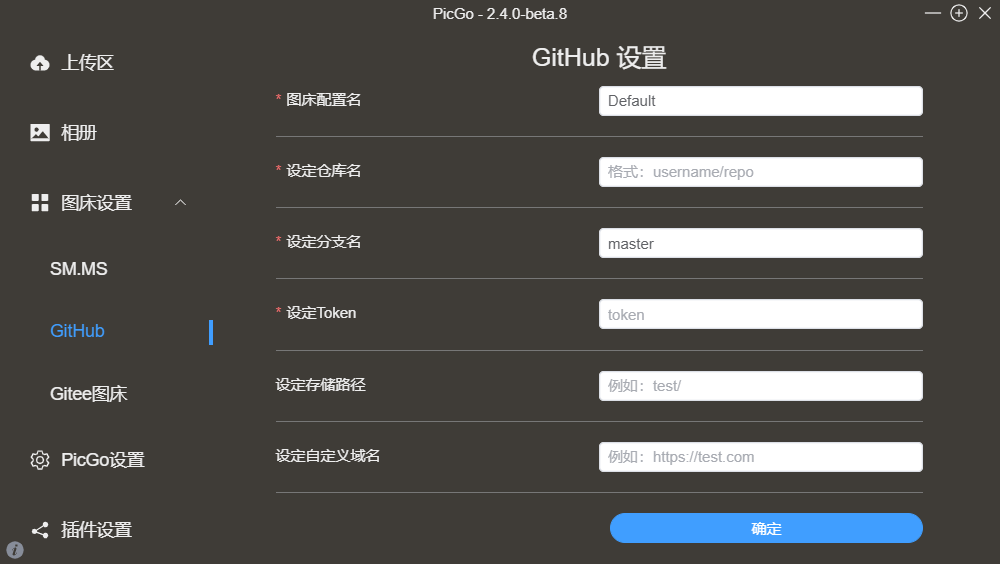
gite+picgo+typora打造个人免费笔记软件
文章目录 1️⃣个人笔记软件2️⃣ 配置教程2.1 使用软件2.2 node 环境配置2.3 软件安装2.4 gite仓库设置2.5 配置picgo2.6 测试检验2.7 github教程 🎡 完结撒花 1️⃣个人笔记软件 最近换了环境,没有之前的生产环境舒适,写笔记也没有劲头&…...

只用 CSS 能玩出什么花样?
在前端开发领域,CSS 不仅仅是一种样式语言,它更像是一位多才多艺的艺术家,能够创造出令人惊叹的视觉效果。本文将带你探索 CSS 的无限可能,从基本形状到动态动画,从几何艺术到仿生设计,只用 CSS 就能玩出令…...

Linux C++ 056-设计模式之迭代器模式
Linux C 056-设计模式之迭代器模式 本节关键字:Linux、C、设计模式、迭代器模式 相关库函数: 概念 迭代器模式(Iterator Pattern)是一种常用的设计模式。迭代器模式提供一种方法顺序访问一个聚合对象中的各个元素,而…...

【Elasticsearch7.11】reindex问题
参考博文链接 问题:reindex 时出现如下问题 原因:数据量大,kibana的问题 解决方法: 将DSL命令转化成CURL命令在服务上执行 CURL命令 自动转化 curl -XPOST "http://IP:PORT/_reindex" -H Content-Type: application…...

nginx代理缓存
在服务器架构中,反向代理服务器除了能够起到反向代理的作用之外,还可以缓存一些资源,加速客户端访问,nginx的ngx_http_proxy_module模块不仅包含了反向代理的功能还包含了缓存功能。 1、定义代理缓存规则 参数详解: p…...

[React 进阶系列] useSyncExternalStore hook
[React 进阶系列] useSyncExternalStore hook 前情提要,包括 yup 的实现在这里:yup 基础使用以及 jest 测试 简单的提一下,需要实现的功能是: yup schema 需要访问外部的 storage外部的 storage 是可变的React 内部也需要访问同…...

Linux C++ 055-设计模式之状态模式
Linux C 055-设计模式之状态模式 本节关键字:Linux、C、设计模式、状态模式 相关库函数: 概念 状态模式(State Pattern)是设计模式的一种,属于行为模式。允许一个对象在其内部状态改变时改变它的行为。对象看起来似…...

景联文科技构建高质量心理学系知识图谱,助力大模型成为心理学科专家
心理大模型正处于快速发展阶段,在临床应用、教育、研究等多个领域展现出巨大潜力。 心理学系知识图谱能够丰富心理大模型的认知能力,使其在处理心理学相关问题时更加精确、可靠和有洞察力。这对于提高心理健康服务的质量和效率、促进科学研究以及优化教育…...

【数学建模】——数学规划模型
目录 一、线性规划(Linear Programming) 1.1 线性规划的基本概念 1.2 线性规划的图解法 模型建立: 二、整数规划(Integer Programming) 2.1 整数规划的基本概念 2.2 整数规划的求解方法 三、非线性规划&#x…...

卸载linux 磁盘的内容,磁盘占满
Linux清理磁盘 https://www.cnblogs.com/siyunianhua/p/17981758 当前文件夹下,数量 ls -l | grep "^-" | wc -l ls -lR | grep "^-" | wc -l 找超过100M的大文件 find / -type f -size 100M -exec ls -lh {} \; df -Th /var/lib/docker 查找…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
