机器学习笔记之集成学习(四)Gradient Boosting
机器学习笔记之集成学习——Gradient Boosting
引言
上一节介绍了Boosting\text{Boosting}Boosting算法思想。并以加性模型的AdaBoost\text{AdaBoost}AdaBoost为例,介绍了理论推导过程。本节将继续介绍Boosting\text{Boosting}Boosting算法系列的另一个样例——Gradient Boosting\text{Gradient Boosting}Gradient Boosting。
回顾:Boosting\text{Boosting}Boosting算法思想与AdaBoost\text{AdaBoost}AdaBoost
关于Boosting\text{Boosting}Boosting算法思想可表示为:在迭代过程中,通过不断学习出新的基学习器ht(x)(t=1,2,⋯,T)h_t(x)(t=1,2,\cdots,\mathcal T)ht(x)(t=1,2,⋯,T),使得它们能够更关注之前迭代过程中的基学习器预测误差较大的样本,最终使得基学习器融合的强学习器 能够覆盖更多的样本,并使得这些样本的预测偏差较小。
基于加性模型的AdaBoost\text{AdaBoost}AdaBoost算法描述表示如下:
这里仅描述的是‘二分类任务’,关于样本标签y(i)(i=1,2,⋯,N)∈{−1,+1}y^{(i)}(i=1,2,\cdots,N) \in \{-1,+1\}y(i)(i=1,2,⋯,N)∈{−1,+1}.
| 输入(Input)(\text{Input})(Input) | 训练集D={x(i),y(i)}i=1N\mathcal D = \{x^{(i)},y^{(i)}\}_{i=1}^ND={x(i),y(i)}i=1N;基学习算法K\mathcal KK;迭代次数T\mathcal TT |
|---|---|
| 初始化(Initialization\text{Initialization}Initialization) | Dinit=1N\begin{aligned} \mathcal D_{init} = \frac{1}{N}\end{aligned}Dinit=N1 |
| 算法过程(Algorithmic Process\text{Algorithmic Process}Algorithmic Process) | 1.1.1. for t=1,2,⋯,Tt=1,2,\cdots,\mathcal Tt=1,2,⋯,T do: 2.2.2. ht=K(D,Dt);h_t = \mathcal K(\mathcal D,\mathcal D_t);ht=K(D,Dt); 3.3.3. ϵt=Px∼Dt[ht(x)≠f(x)]\epsilon_t = \mathcal P_{x \sim \mathcal D_t} \left[h_t(x) \neq f(x)\right]ϵt=Px∼Dt[ht(x)=f(x)] 4.4.4. if ϵt>0.5:\epsilon_t > 0.5:ϵt>0.5: 5.5.5. break 6.6.6. else 7.7.7. αt=12ln(1−ϵtϵt)\alpha_t = \frac{1}{2} \ln \left(\frac{1 - \epsilon_t}{\epsilon_t}\right)αt=21ln(ϵt1−ϵt) 8.8.8. Dt+1=1Zt⋅Dt⋅exp{−f(x)⋅αtht}\mathcal D_{t+1} = \frac{1}{\mathcal Z_t} \cdot \mathcal D_t \cdot \exp\{-f(x) \cdot \alpha_th_t\}Dt+1=Zt1⋅Dt⋅exp{−f(x)⋅αtht} 9.9.9. end for |
| 输出(Output\text{Output}Output) | H(x)=Sign(∑t=1Tαtht)\mathcal H(x) = \text{Sign}(\sum_{t=1}^{\mathcal T} \alpha_th_t)H(x)=Sign(∑t=1Tαtht) |
观察上述算法,对于学习出的基学习器ht=K(D,Dt)h_t = \mathcal K(\mathcal D,\mathcal D_t)ht=K(D,Dt),其中Dt\mathcal D_tDt表示样本的采样权重。也可以理解为样本被关注的程度。
以555个样本组成的数据集为例,初始状态下,它们各自的权重信息是相等状态:
Dinit⇒[15,15,15,15,15]\mathcal D_{init} \Rightarrow \left[\frac{1}{5},\frac{1}{5},\frac{1}{5},\frac{1}{5},\frac{1}{5}\right]Dinit⇒[51,51,51,51,51]
经过ttt次迭代后,得到的权重结果可能是这个样子:
Dt⇒[110,110,25,15,15]\mathcal D_t \Rightarrow \left[\frac{1}{10},\frac{1}{10},\frac{2}{5},\frac{1}{5},\frac{1}{5}\right]Dt⇒[101,101,52,51,51]
比较这两组权重,可以发现:对于样本的关注度转移了。可以想象:
- 对于x(1),x(2)x^{(1)},x^{(2)}x(1),x(2)两个样本,ttt次迭代之前学习的基学习器h1,⋯,ht−1h_1,\cdots,h_{t-1}h1,⋯,ht−1相比之下能够较容易地将这两个样本预测正确;
- 相反,被分配权重较高的样本,如样本x(3)x^{(3)}x(3),它就需要当前迭代的基学习器hth_tht进行学习。如果依然有f(x(3))≠ht(x(3))f(x^{(3)})\neq h_t(x^{(3)})f(x(3))=ht(x(3)),只能再次分配权重,让t+1t+1t+1次迭代的基学习器ht+1h_{t+1}ht+1去学习x(3)x^{(3)}x(3),以此类推。
通过上面的算法流程,可以发现:关于权重分布Dt\mathcal D_tDt,它并不是我们想要关注的对象。我们真正关注的对象只有αt\alpha_tαt和hth_tht。它的更新顺序表示为:
Dinit⇒h1,α1⇒D1⇒⋯⇒DT−1⇒hT,αT⇒DT\mathcal D_{init} \Rightarrow h_1,\alpha_1 \Rightarrow \mathcal D_1 \Rightarrow \cdots \Rightarrow \mathcal D_{\mathcal T-1} \Rightarrow h_{\mathcal T},\alpha_{\mathcal T} \Rightarrow \mathcal D_{\mathcal T}Dinit⇒h1,α1⇒D1⇒⋯⇒DT−1⇒hT,αT⇒DT
关于加性模型的AdaBoost\text{AdaBoost}AdaBoost,在每次迭代学习新的基学习器 过程中,我们只是对训练集D\mathcal DD进行重新赋权(Re-Weighting\text{Re-Weighting}Re-Weighting)操作。那么对于不接受带权样本的基学习算法K′\mathcal K'K′,可以使用重采样(Re-Sampling\text{Re-Sampling}Re-Sampling)实现。
机器学习(周志华著)P177.
-
不同于重新赋权操作,ttt次迭代过程中重采样操作产生的Dt\mathcal D_tDt不再是权重分布,而是真真正正的以t−1t-1t−1次迭代过程中未被学习正确的样本为主体的样本集合。
-
一般情况下,无论是重新赋权,还是重采样,两种方法没有优劣区别。但重新赋权方法中需要判别ϵt=Px∼Dt[ht(x)≠f(x)]\epsilon_t = \mathcal P_{x \sim \mathcal D_t} \left[h_t(x) \neq f(x)\right]ϵt=Px∼Dt[ht(x)=f(x)]的结果是否满足条件,如果不满足条件,会提前停止迭代。
相反,如果是重采样方法,相当于每一次迭代均重新设置训练集,只要训练集内有样本,就不会出现停止迭代的情况。因而可以持续到预设的T\mathcal TT轮迭代完成。
由于概率密度积分的约束,因而权重之和必然是1 -> 不会出现采不到样本的情况。
Gradient Boosting\text{Gradient Boosting}Gradient Boosting算法介绍
场景构建
依然假设数据集合D={(x(i),y(i))}i=1N\mathcal D =\{(x^{(i)},y^{(i)})\}_{i=1}^ND={(x(i),y(i))}i=1N,并且定义一个初始状态下预测模型Hinit(x)\mathcal H_{init}(x)Hinit(x),并初始化它的模型结果:
Hinit(x(i))=0i=1,2,⋯,N\mathcal H_{init}(x^{(i)}) = 0 \quad i=1,2,\cdots,NHinit(x(i))=0i=1,2,⋯,N
算法过程
这里以第ttt次迭代为例,并且假设我们基于数据集D\mathcal DD处理一个回归任务:
-
在t−1t-1t−1次迭代后我们得到的数据集合Dt−1\mathcal D_{t-1}Dt−1表示如下:
Dt−1={(x(i),y(i)−Ht−1(x(i)))}i=1N\mathcal D_{t-1} = \{(x^{(i)},y^{(i)} - \mathcal H_{t-1}(x^{(i)}))\}_{i=1}^NDt−1={(x(i),y(i)−Ht−1(x(i)))}i=1N
其中,样本特征x(i)(i=1,2,⋯,N)x^{(i)}(i=1,2,\cdots,N)x(i)(i=1,2,⋯,N)未发生变化;而对应标签表示为真实标签y(i)y^{(i)}y(i)与t−1t-1t−1时刻预测模型Ht−1(x)\mathcal H_{t-1}(x)Ht−1(x)关于对应样本x(i)x^{(i)}x(i)的预测结果Ht−1(x(i))\mathcal H_{t-1}(x^{(i)})Ht−1(x(i))之间的残差信息(Residuals\text{Residuals}Residuals):
当t=1t=1t=1时,H0(x(i))=Hinit(x(i))=0\mathcal H_0(x^{(i)}) = \mathcal H_{init}(x^{(i)}) = 0H0(x(i))=Hinit(x(i))=0。这意味着‘初始时刻’就在原始的数据集合D\mathcal DD上进行训练。
y(i)−Ht−1(x(i))y^{(i)} - \mathcal H_{t-1}(x^{(i)})y(i)−Ht−1(x(i)) -
以Dt−1\mathcal D_{t-1}Dt−1作为第ttt次迭代步骤的数据集,并通过学习算法K\mathcal KK从该数据集训练出一个新的基学习器(Base Learner\text{Base Learner}Base Learner)hth_tht:
ht=K(Dt−1)h_t = \mathcal K(\mathcal D_{t-1})ht=K(Dt−1)
这意味着:hth_tht作为学习的并不是关于真实标签的信息,而是t−1t-1t−1时刻的预测模型Ht−1(x)\mathcal H_{t-1}(x)Ht−1(x)对于真实标签拟合不足的部分。也就是说,Ht−1(x)\mathcal H_{t-1}(x)Ht−1(x)对于真实标签没有拟合的部分,由新训练的基学习器hth_tht去拟合。 -
按照上述逻辑,我们需要将t−1t-1t−1时刻预测模型Ht−1(x)\mathcal H_{t-1}(x)Ht−1(x)与ttt时刻的基学习器hth_tht做融合,得到ttt时刻的预测模型Ht(x)\mathcal H_t(x)Ht(x):
Ht(x)=Ht−1(x)+η⋅ht\mathcal H_{t}(x) = \mathcal H_{t-1}(x) + \eta \cdot h_tHt(x)=Ht−1(x)+η⋅ht
观察上式可以发现,多了一个学习率(Learning Rate\text{Learning Rate}Learning Rate)η\etaη。它本质上式一个正则项,也被称作基学习器hth_tht的收缩(Shrinkage\text{Shrinkage}Shrinkage)。从常规逻辑的角度,既然hth_tht能够对残差训练集Dt−1\mathcal D_{t-1}Dt−1进行拟合,那么应该将hth_tht与Ht−1(x)\mathcal H_{t-1}(x)Ht−1(x)直接融合即可。即η=1\eta = 1η=1。但真实情况是,这种做法可能会导致过拟合(Overfitting)(\text{Overfitting})(Overfitting)。因为不断拟合残差的过程,最终可能导致:除去初始的若干次迭代之外,剩余的迭代中基学习器拟合的信息绝大多数是数据的噪声信息。因而使用学习率来约束基学习器hth_tht的拟合信息。
迭代过程与梯度下降法之间的关联关系
关于Ht(x)\mathcal H_t(x)Ht(x)的迭代过程类似于梯度下降法(Gradient Descent,GD\text{Gradient Descent,GD}Gradient Descent,GD),不同于梯度下降法的点在于:直接对预测模型自身求解梯度,而不是对模型参数。针对回归任务的目标函数,我们选择均方误差(Mean-Square Error,MSE\text{Mean-Square Error,MSE}Mean-Square Error,MSE):
L=1N∑i=1N(y(i)−ypred(i))2\mathcal L = \frac{1}{N} \sum_{i=1}^N \left(y^{(i)} - y_{pred}^{(i)}\right)^2L=N1i=1∑N(y(i)−ypred(i))2
- 由于样本之间独立同分布(Independent Identically Distribution,IID\text{Independent Identically Distribution,IID}Independent Identically Distribution,IID)这里仅观察某一个样本标签y(i)y^{(i)}y(i)的目标函数信息:
L(i)=1N(y(i)−ypred(i))2\mathcal L^{(i)} = \frac{1}{N}\left(y^{(i)} - y_{pred}^{(i)}\right)^2L(i)=N1(y(i)−ypred(i))2 - 假设迭代到ttt时刻停止,那么此时的预测模型就是Ht(x)\mathcal H_t(x)Ht(x)。因而关于样本标签y(i)y^{(i)}y(i)的预测结果ypred(i)y_{pred}^{(i)}ypred(i)为:
ypred(i)=Ht(x(i))y_{pred}^{(i)} = \mathcal H_t(x^{(i)})ypred(i)=Ht(x(i)) - 根据定义,我们希望基学习器hth_tht能够拟合Ht−1(x)\mathcal H_{t-1}(x)Ht−1(x)拟合不足的部分。关于样本(x(i),y(i))(x^{(i)},y^{(i)})(x(i),y(i)),有:
ht(x(i))=y(i)−Ht−1(x(i))h_t(x^{(i)}) = y^{(i)} - \mathcal H_{t-1}(x^{(i)})ht(x(i))=y(i)−Ht−1(x(i)) - 至此,基于上述逻辑关系,我们要求解样本(x(i),y(i))(x^{(i)},y^{(i)})(x(i),y(i))对应的目标函数L(i)\mathcal L^{(i)}L(i)对t−1t-1t−1时刻的预测模型Ht−1(x(i))\mathcal H_{t-1}(x^{(i)})Ht−1(x(i))的梯度:
∂L(i)∂Ht−1(x(i))\frac{\partial \mathcal L^{(i)}}{\partial \mathcal H_{t-1}(x^{(i)})}∂Ht−1(x(i))∂L(i)
根据链式求导法则,可以将其拆成两项:
后续梯度∂L(i)∂Ht−1(x(i))\begin{aligned}\frac{\partial \mathcal L^{(i)}}{\partial \mathcal H_{t-1}(x^{(i)})}\end{aligned}∂Ht−1(x(i))∂L(i)使用符号I\mathcal II替代。
I=∂L(i)∂Ht(x(i))⋅∂Ht(x(i))∂Ht−1(x(i))\mathcal I = \frac{\partial \mathcal L^{(i)}}{\partial \mathcal H_{t}(x^{(i)})} \cdot \frac{\partial \mathcal H_t(x^{(i)})}{\partial \mathcal H_{t-1}(x^{(i)})}I=∂Ht(x(i))∂L(i)⋅∂Ht−1(x(i))∂Ht(x(i))
观察第一项,将L(i)\mathcal L^{(i)}L(i)代入,有:
也将ypred(i)=Ht(x(i))y_{pred}^{(i)} = \mathcal H_t(x^{(i)})ypred(i)=Ht(x(i))代入公式。
∂L(i)∂Ht(x(i))=1N⋅2×(y(i)−ypred(i))⋅[0−1]=−2N[y(i)−Ht(x(i))]\begin{aligned} \frac{\partial \mathcal L^{(i)}}{\partial \mathcal H_{t}(x^{(i)})} & = \frac{1}{N} \cdot 2 \times(y^{(i)} - y_{pred}^{(i)}) \cdot [0 - 1] \\ & = - \frac{2}{N} \left[y^{(i)} - \mathcal H_{t}(x^{(i)})\right] \end{aligned}∂Ht(x(i))∂L(i)=N1⋅2×(y(i)−ypred(i))⋅[0−1]=−N2[y(i)−Ht(x(i))]
观察第二项,它的结果为:
这里η⋅ht(x(i))\eta \cdot h_t(x^{(i)})η⋅ht(x(i))与Ht−1(x(i))\mathcal H_{t-1}(x^{(i)})Ht−1(x(i))之间无关,视作常数,导数结果为000.
∂Ht(x(i))∂Ht−1(x(i))=∂∂Ht−1(x(i))[Ht−1(x(i))+η⋅ht(x(i))]=1+0=1\begin{aligned}\frac{\partial \mathcal H_t(x^{(i)})}{\partial \mathcal H_{t-1}(x^{(i)})} & = \frac{\partial}{\partial \mathcal H_{t-1}(x^{(i)})} \left[\mathcal H_{t-1}(x^{(i)}) + \eta \cdot h_t(x^{(i)})\right] \\ & = 1 + 0 \\ & = 1 \end{aligned}∂Ht−1(x(i))∂Ht(x(i))=∂Ht−1(x(i))∂[Ht−1(x(i))+η⋅ht(x(i))]=1+0=1
至此,梯度结果I\mathcal II表示如下:
将ht(x(i))=y(i)−Ht−1(x(i))h_t(x^{(i)}) = y^{(i)} - \mathcal H_{t-1}(x^{(i)})ht(x(i))=y(i)−Ht−1(x(i))代入到公式中。
I=−2N[y(i)−Ht(x(i))]×1=−2N[y(i)−Ht−1(x(i))−η⋅ht(x(i))]=−2N(1−η)⋅ht(x(i))\begin{aligned} \mathcal I & = -\frac{2}{N} \left[y^{(i)} - \mathcal H_t(x^{(i)})\right] \times 1 \\ & = -\frac{2}{N} \left[y^{(i)} - \mathcal H_{t-1}(x^{(i)}) - \eta \cdot h_t(x^{(i)})\right] \\ & = -\frac{2}{N} (1 - \eta) \cdot h_t(x^{(i)}) \end{aligned}I=−N2[y(i)−Ht(x(i))]×1=−N2[y(i)−Ht−1(x(i))−η⋅ht(x(i))]=−N2(1−η)⋅ht(x(i)) - 此时梯度中,2N(1−η)\begin{aligned}\frac{2}{N}(1 - \eta)\end{aligned}N2(1−η)仅是一个描述梯度大小的系数,和方向无关。因而可以继续化简为如下形式:
I=∂L(i)∂Ht−1(x(i))∝−ht(x(i))\mathcal I = \frac{\partial \mathcal L^{(i)}}{\partial \mathcal H_{t-1}(x^{(i)})} \propto - h_t(x^{(i)})I=∂Ht−1(x(i))∂L(i)∝−ht(x(i))
此时再回顾预测模型的迭代公式,可以将其转化为:
Ht(x(i))=Ht−1(x(i))+η⋅ht(x(i))⇒Ht(x(i))=Ht−1(x(i))−η⋅∂L(i)∂Ht−1(x(i))\begin{aligned} & \quad \mathcal H_t(x^{(i)}) = \mathcal H_{t-1}(x^{(i)}) + \eta \cdot h_t(x^{(i)}) \\ & \Rightarrow \mathcal H_{t}(x^{(i)}) = \mathcal H_{t-1}(x^{(i)}) - \eta \cdot \frac{\partial \mathcal L^{(i)}}{\partial \mathcal H_{t-1}(x^{(i)})} \end{aligned}Ht(x(i))=Ht−1(x(i))+η⋅ht(x(i))⇒Ht(x(i))=Ht−1(x(i))−η⋅∂Ht−1(x(i))∂L(i)
可以看出,这就是一个梯度下降的标准公式。这说明基学习器hth_tht,它的方向与梯度优化的方向相反。
这里是针对视频中The residuals equal to −∂L∂Hif using MSE as the loss.\begin{aligned}\text{The residuals equal to }-\frac{\partial \mathcal L}{\partial \mathcal H} \text{ if using MSE as the loss.}\end{aligned}The residuals equal to −∂H∂L if using MSE as the loss.的一个推导解释。
需要注意的是,一些其他的Boosting\text{Boosting}Boosting函数,也可以套用到Gradient Boosting\text{Gradient Boosting}Gradient Boosting这个框架下面。这里仅以回归任务(均方误差)示例描述。
下一节将针对基学习器方向与梯度方向相反的性质介绍梯度提升树(Gradient Boosting Decision Tree,GBDT\text{Gradient Boosting Decision Tree,GBDT}Gradient Boosting Decision Tree,GBDT)
相关参考:
5.3 Boosting【斯坦福21秋季:实用机器学习中文版】
机器学习(周志华著)
相关文章:
Gradient Boosting)
机器学习笔记之集成学习(四)Gradient Boosting
机器学习笔记之集成学习——Gradient Boosting引言回顾:Boosting\text{Boosting}Boosting算法思想与AdaBoost\text{AdaBoost}AdaBoostGradient Boosting\text{Gradient Boosting}Gradient Boosting算法介绍场景构建算法过程迭代过程与梯度下降法之间的关联关系引言 …...
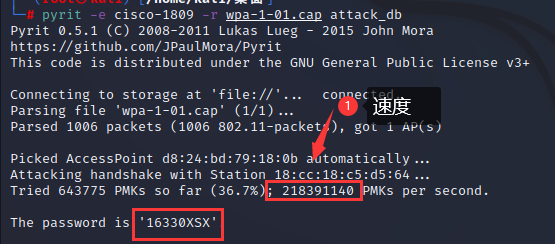
WPA渗透-pyrit:batch-table加速attack_db模块加速_“attack_db”模块加速
WPA渗透-pyrit:batch-table加速attack_db模块加速_“attack_db”模块加速 1.渗透WIFI 1.导入密码字典 pyrit -i 字典文件 import_passwords -i:输入的文件名 import_passwords:从类文件源导入密码。pyrit -i pwd.txt import_passwords2.导…...

kotlin第二部分复习纪要
扩展函数。 例如: fun Context.toast(msg: String, length: Int Toast.LENGTH_SHORT){Toast.makeText(this, msg, length).show() } 使用 val activity: Context? getActivity() activity?.toast("Hello world!") activity?.toast("Hello worl…...
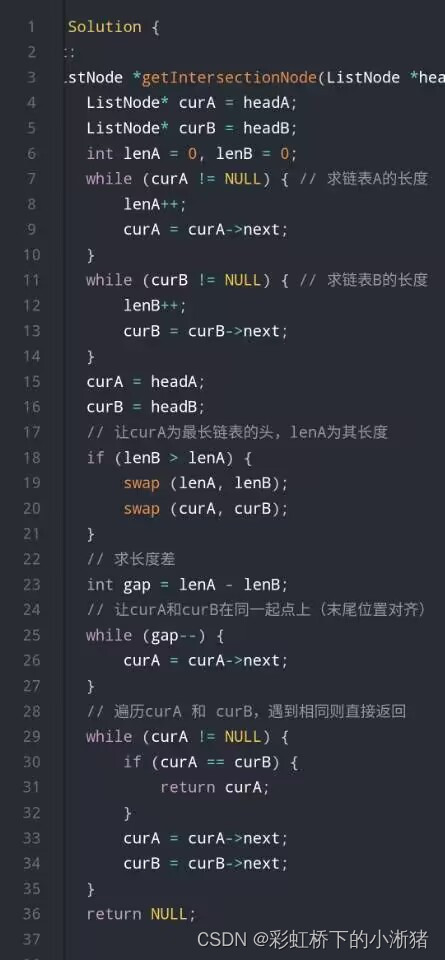
代码随想录--链表--删除链表第n个节点题型、链表相交题型
删除链表第n个节点题型 链表遍历学清楚! | LeetCode:19.删除链表倒数第N个节点 (opens new window) 这道题我一开始想的是,倒数第n个节点,链表不方便往前找,那就从链表头结点开始找链表长度减n,这时候就是…...
一起来学5G终端射频标准(In-band emissions-2)
上一篇我们列出了IBE的测试要求表格,今天我们详细说一下IBE如何测量计算,以及CA/NR-DC/SUL/UL-MIMO/V2X/Tx Diversity模式下的IBE情况。01—IBE如何测量和计算IBE的测试是对落入到未被分配的RB的干扰的测量,为12个子载波的平均发射功率&#…...

硬刚ChatGPT,中国版ChatGPT“狂飙”的机会在哪儿?
整体来讲,个人的态度是积极的。 ChatGPT、文心一言 都是在多重因素及大量 AI 模型/数据 长时间累积的成果,不是一蹴而就,立竿见影的功能产品。两者产生的基础和背景均不相同,各有优劣,不存在强行对比的概念。 以下是 …...

ReactNative——导航器createBottomTabNavigator(底部标签导航器篇)
上一篇有讲到堆栈式导航器的写法,点这里->堆栈式导航器标签导航器官网链接先安装依赖包yarn add react-navigation/bottom-tabs接着在src/navigator文件夹下新建BottomTabs.tsx文件,写法跟堆栈式导航器类似的~import React from react; import { NavigationConta…...
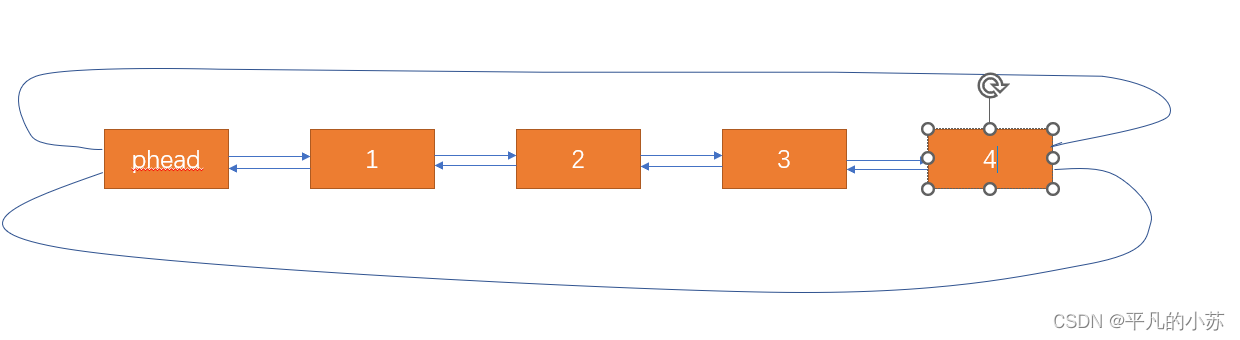
【数据结构】带头双向循环链表的实现
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 🚀数据结构专栏ÿ…...
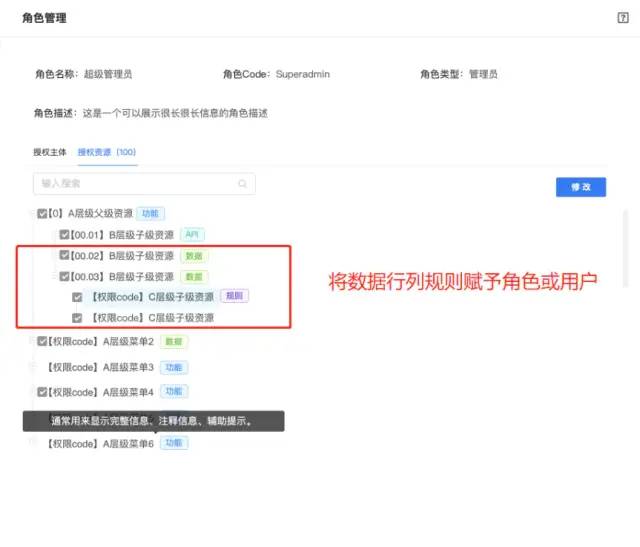
软件开发的权限系统功能模块设计,分享主流的九种常见权限模型
软件系统的权限控制几乎是非常常见且必备的,这篇文章整理下常见的九种模型,几乎基本够你用了,主流的权限模型主要有以下9种: 1、ACL模型 访问控制列表 2、DAC模型 自主访问控制 3、MAC模型 强制访问控制 4、ABAC模型 基于属性的访…...
CSS3-数据可视化
2D动画 - transform CSS3 transform属性允许你旋转,缩放,倾斜或平移给定元素。 Transform是形变的意思(通常也叫变换),transformer就是变形金刚 常见的函数transform function有: 平移:transl…...
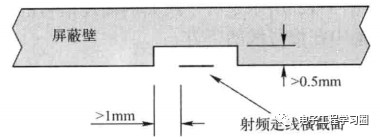
硬件系统工程师宝典(15)-----PCB上的EMC设计,“拿捏了”
各位同学大家好,欢迎继续做客电子工程学习圈,今天我们继续来讲这本书,硬件系统工程师宝典。上篇我们说到PCB常用的多层板叠层结构,综合成本、性能、需求考虑选择不同的叠层结构。今天我们来看看为提高EMC性能,在PCB设计…...
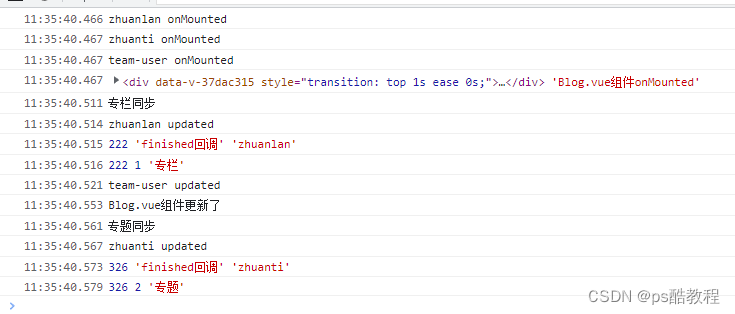
vue3滚动条滚动后元素固定
代码地址:https://gitee.com/zzhua195/easyblog-web-vuee Framework.vue 在这个布局组件中,监听main的滚动事件,获取滚动的距离,将它存入store,以便其它组件能够共享,监听到 <template><div c…...
新吲哚菁绿染料IR-825 NHS,IR825 NHS ester,IR825 SE,IR-825 活性酯,用于科研实验研究和临床
IR825 NHS理论分析:中文名:新吲哚菁绿-琥珀酰亚胺酯,IR-825 琥珀酰亚胺酯,IR-825 活性酯英文名:IR825 NHS,IR-825 NHS,IR825 NHS ester,IR825 SECAS号:N/AIR825 NHS产品详…...
的定义及使用)
GO语言--接口(interface)的定义及使用
接口定义 接口也是一种数据类型,它代表一组方法的集合。 接口是非侵入式的。即接口设计者无需知道接口被哪些类型实现,而接口使用者只需知道实现怎样的接口,并且无须指明实现哪一个接口。编译器在编译时就会知道哪个类型实现哪个接口&#…...

【Python语言基础】——Python MongoDB 查询
Python语言基础——Python MongoDB 查询 文章目录 Python语言基础——Python MongoDB 查询一、Python MongoDB 查询一、Python MongoDB 查询 筛选结果 在集合中查找文档时,您能够使用 query 对象过滤结果。 find() 方法的第一个参数是 query 对象,用于限定搜索。 实例 查找地…...

第十四届蓝桥杯模拟赛【第三期】Python
1 进制转换 问题描述 请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。 请将这个数的十进制形式作为答案提交。 答案:2730 def ch…...
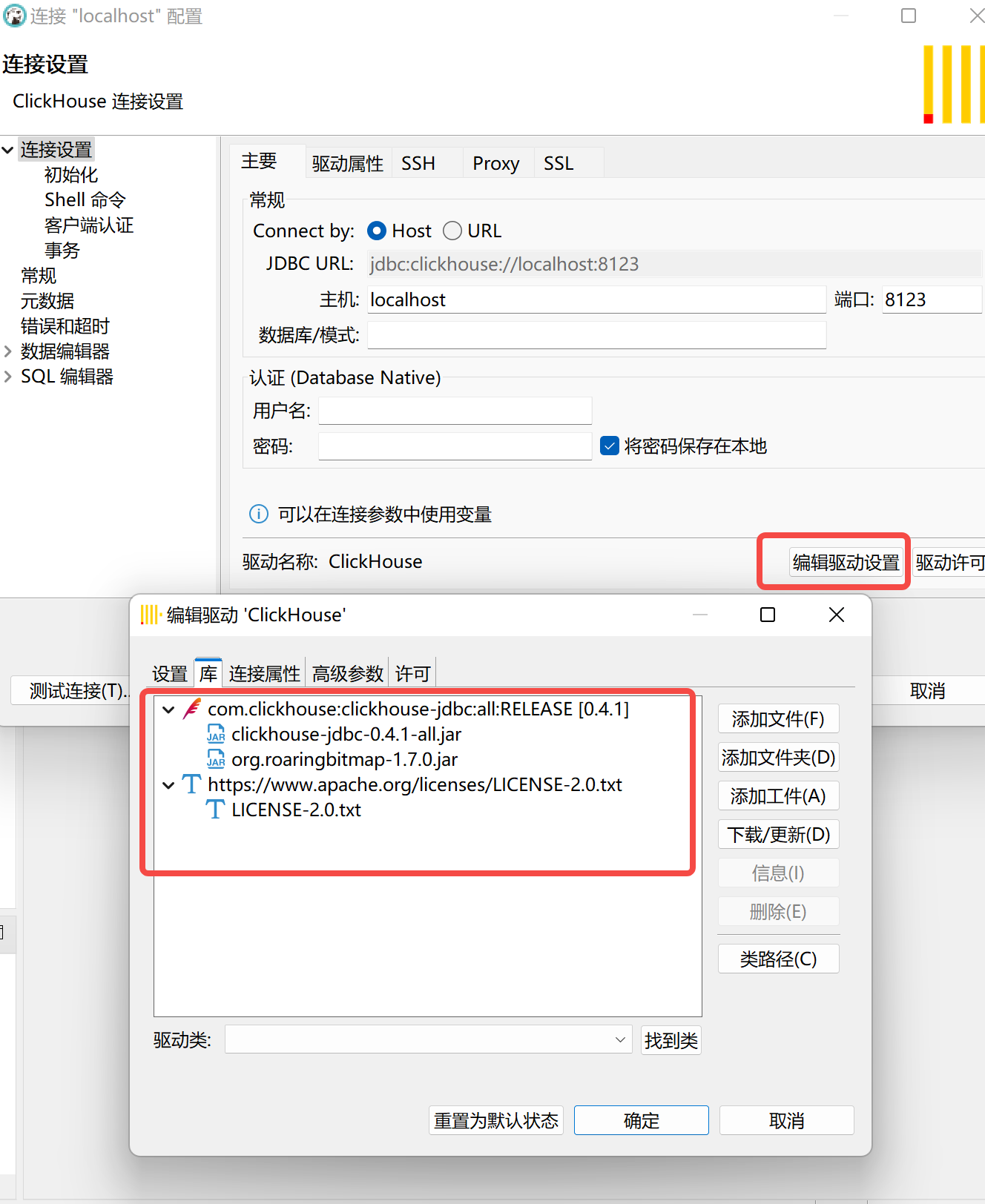
windows 下docker 安装clickhouse
docker 下载https://www.docker.com/products/docker-desktop/将下载下来的Docker Desktop Installer.exe文件双击进行安装即可,安装完成后,任务栏会出现一个蓝色的小鲸鱼图标(注意安装完成后可能会重启系统)Docker Desktop如果出…...

【华为OD机试真题 JAVA】TLV编码问题
标题:TLV编码问题 | 时间限制:1秒 | 内存限制:262144K | 语言限制:不限 TLV编码是按TagLengthValue格式进行编码的,一段码流中的信元用tag标识,tag在码流中唯一不重复,length表示信元value的长度,value表示信元的值,码流以某信元的tag开头,tag固定占一个字节,lengt…...
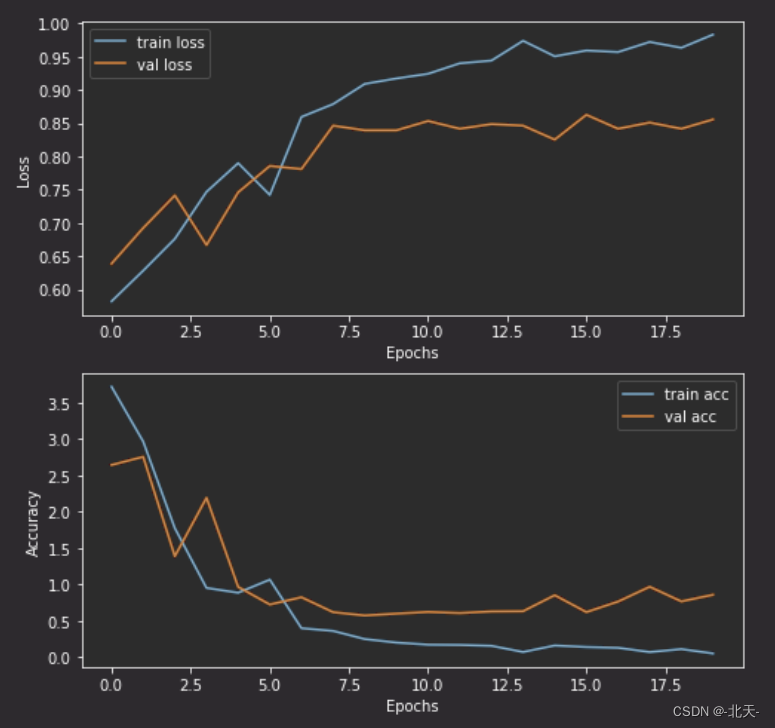
深度学习 Day26——使用Pytorch实现猴痘病识别
深度学习 Day26——使用Pytorch实现猴痘病识别 文章目录深度学习 Day26——使用Pytorch实现猴痘病识别一、前言二、我的环境三、前期工作1、设置GPU导入依赖项2、导入猴痘病数据集3、划分数据集四、构建CNN网络五、训练模型1、设置超参数2、编写训练函数3、编写测试函数4、正式…...

redis简单介绍
对于一名前端工程师,想要进阶成为全栈工程师,redis技术是我们一定需要掌握的。作为当前非关系型数据库Nosql中比较热门的key-value存储系统,了解redis的原理和开发是极其重要的。本文我会循序渐进的带领大家一步步认识redis,使用r…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
