算法工程师第十四天（找树左下角的值 路径总和 从中序与后序遍历序列构造二叉树 ）

参考文献 代码随想录

一、找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

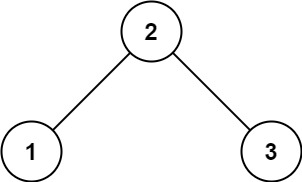
输入: root = [2,1,3]
输出: 1

示例 2:

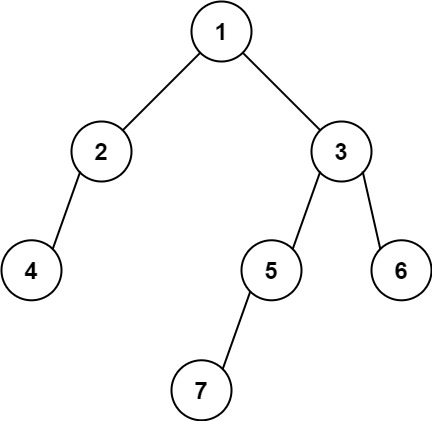
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

层次遍历：收集每一层的结果，然后取最后一层的第一个值

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):def findBottomLeftValue(self, root):""":type root: TreeNode:rtype: int"""# 层次遍历from collections import dequequeen = deque()  # 使用队列存储数据ans = deque()  # 存放每层的结果if root:queen.append(root)while queen:count = len(queen)  # 记录每层的个数tmp = [] # 暂时存放每一层的结果while count:  # 出队列node = queen.popleft()# 收集结果tmp.append(node.val)# 收集每层的结果，左边和右边同时收集，为什么能呢，因为count是记录着每一层的节点数，这样才能控制要收集左右孩子多少个if node.left:queen.append(node.left)  # 判断左边是右值，如果有，则进入队列if node.right:queen.append(node.right)count -= 1# 把每一层的结果放入最后的结果集中ans.append(tmp)return ans[len(ans) - 1][0]

前序遍历：求所以路径

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):def findBottomLeftValue(self, root):""":type root: TreeNode:rtype: int"""# 层次遍历from collections import dequetmp = []  # 使用队列存储数据ans = [0 for _ in range(10001)] # 存放每层的结果，为什么要初始化呢，因为我们存储的是每一条路基，而我们只需要输出最长路径并且是最左边的，ans[i]代表的是路径长度为i的路径ans[i]if not root:return 0def dfs(cur):if not cur:  # 说明当前节点为零return 0# 中tmp.append(cur.val)  # 收集每条路的节点if not cur.left and not cur.right:  # 说明到了叶子节点if not ans[len(tmp)]:  # 因为这个遍历的顺序是中左右，所以先收集的结果是左边的，为了防止长度相等的路，所以一旦有值，就不重新赋值了，这样就收集了长度相等的最左边的ans[len(tmp)] = tmp[:]return # 左 tmp = [1, 2]if cur.left:  # 判断左边是否有左孩子，如果有，那么就一直到低，碰到叶子节点就回收dfs(cur.left)  # 结束收集左边的节点，如果遇到了那么本次的循环就终止掉，然后到上一层循环，因为这个递归是一个套娃的左右就像 f(f(f(f(x))))，无限的套进去，最里面的函数终止了，说明就不往下走了，那么就开始执行每次的函数，第一次函数是执行2，然在到1，tmp.pop()  # 回溯 然后回退一个，if cur.right:  # 判断回退的这个节点是否有有孩子，如果有那就往右边找，如果没有，那么将会进入到有没有左孩子dfs(cur.right,)tmp.pop()dfs(root)for i in range(10000, -1, -1):if ans[i]:return ans[i][-1]

递归：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):def findBottomLeftValue(self, root):""":type root: TreeNode:rtype: int"""""" 问题分析：首先是最底层，然后是左节点，然后判断是否到底最底层呢，就是你比较每次的深度大小，然后只收集最大的叶子点的值"""self.maxD = float("-inf") # 存放的是每次最大深度的结果   self.resul = None  # 存放的是最后的结果# deepth = 0  # 记录每次的叶子长度if not root:return 0self.dfs(root, 0)return self.resuldef dfs(self, cur, deepth):# 没有返回if not cur.left and not cur.right:  # 对比深度，大的话，就跟新result值if deepth > self.maxD:self.maxD = deepthself.resul = cur.valreturn # 左if cur.left:self.dfs(cur.left, deepth + 1)if cur.right:self.dfs(cur.right, deepth + 1)

二、路径总和

        给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

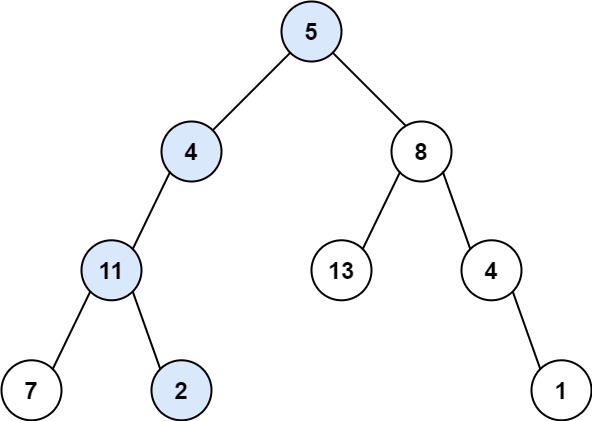
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

递归：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):def hasPathSum(self, root, targetSum):""":type root: TreeNode:type targetSum: int:rtype: bool"""self.tmp = []self.r = []if not root:return Falseself.dfs(root)if targetSum in self.r:return Truereturn Falsedef dfs(self, root):if not root:return 0self.tmp.append(root.val)if not root.left and not root.right:self.r.append(sum(self.tmp))if root.left:self.dfs(root.left)self.tmp.pop()if root.right:self.dfs(root.right)self.tmp.pop()

递归简化版：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):def hasPathSum(self, root, targetSum):""":type root: TreeNode:type targetSum: int:rtype: bool"""self.f = Falseself.r = targetSumif not root:return Falseself.dfs(root, root.val)return self.fdef dfs(self, root, tmp):if not root:return 0if not root.left and not root.right:if tmp == self.r:self.f = Trueif root.left:self.dfs(root.left, tmp + root.left.val)  # tmp + root.left.val回溯，因为递归解释回溯if root.right:self.dfs(root.right,  tmp + root.right.val)

三、路径总和 II

        给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

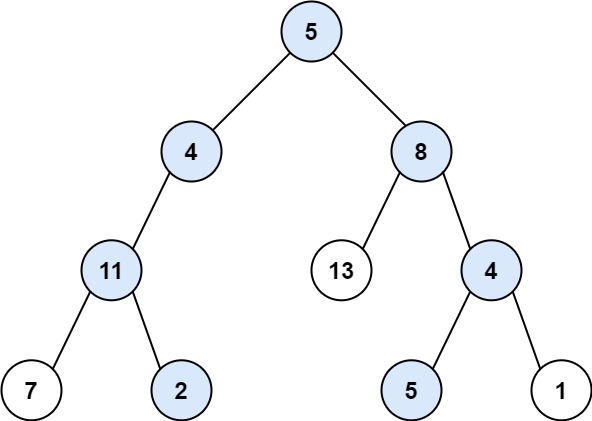
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

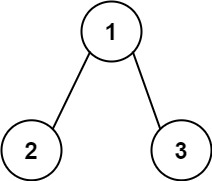
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

问题分析：前序遍历，一个统计和，一个统计节点

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):def pathSum(self, root, targetSum):""":type root: TreeNode:type targetSum: int:rtype: List[List[int]]"""# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = rightself.tmp = []self.r = targetSumif not root:return []self.dfs(root, root.val, [int(root.val)])return self.tmpdef dfs(self, root, tmp, tl):if not root:return 0if not root.left and not root.right:if tmp == self.r:self.tmp.append(tl)if root.left:self.dfs(root.left, tmp + root.left.val, tl + [root.left.val])  # tmp + root.left.val回溯，因为递归解释回溯if root.right:self.dfs(root.right,  tmp + root.right.val, tl + [root.right.val])

四、从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

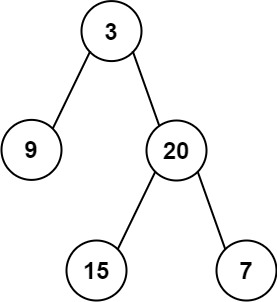
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

class Solution:def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:# 第一步: 特殊情况讨论: 树为空. (递归终止条件)if not postorder:return None# 第二步: 后序遍历的最后一个就是当前的中间节点.root_val = postorder[-1]root = TreeNode(root_val)# 第三步: 找切割点.separator_idx = inorder.index(root_val)# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.inorder_left = inorder[:separator_idx]inorder_right = inorder[separator_idx + 1:]# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.postorder_left = postorder[:len(inorder_left)]postorder_right = postorder[len(inorder_left): len(postorder) - 1]# 第六步: 递归root.left = self.buildTree(inorder_left, postorder_left)root.right = self.buildTree(inorder_right, postorder_right)# 第七步: 返回答案return root