Numpy基础用法
Numpy基础用法
- numpy.all()
- num.sun()
numpy.all()
numpy中的all()函数用于测试 NumPy 数组中所有元素是否都满足指定条件。它接受一个 NumPy
数组作为输入,并返回一个布尔值,指示数组中所有元素是否都满足条件。让我们通过具体的代码示例来深入探讨np.all()
函数的常见应用场景:
-
判断数组中是否全是非零元素:
a = np.array([1, 2, 3, 4]) b = np.array([0, 1, 2, 3]) c = np.array([np.nan, 1, 2, 3]) # nan 表示非零元素 d = np.array([np.inf, 1, 2, 3]) # np.inf 表示正无穷大 e = np.array([-np.inf, 1, 2, 3]) # -np.inf 表示负无穷大print(np.all(a)) # 输出 True print(np.all(b)) # 输出 False print(np.all(c)) # 输出 True print(np.all(d)) # 输出 True print(np.all(e)) # 输出 True -
判断数组中是否存在非零元素:
a = np.array([0, 0, 0, 0]) b = np.array([0, 1, 0, 0]) c = np.array([0, np.nan, 0, 0]) d = np.array([0, np.inf, 0, 0]) e = np.array([0, -np.inf, 0, 0])print(np.any(a)) # 输出 False print(np.any(b)) # 输出 True print(np.any(c)) # 输出 True print(np.any(d)) # 输出 True print(np.any(e)) # 输出 True -
判断数组中的元素是否都满足某个条件:
a = np.array([0, 2, 3, 4]) # 判断数组 a 的元素是否都大于 0 print(np.all(a > 0)) # 输出 False # 判断数组 a 的元素是否都大于 -1 print(np.all(a > -1)) # 输出 Trueb = np.array([0, 0, 0, 0]) # 判断数组 b 是否为全 0 数组 print(np.all(b == 0)) # 输出 True # 判断数组 b 是否为全 1 数组 print(np.all(b == 1)) # 输出 False -
判断两个矩阵所有对应元素是否相等
import numpy as np a = np.array([1,2,3]) b = np.array([4,5,6]) c = np.array([1,2,3]) print((a==b).all()) False print((a==c).all()) True
num.sun()
import cv2
import numpy as np# 读取图像
image = cv2.imread('your_image_path.png')# 找到像素值为 (255, 255, 0) 的像素
blue_pixels = (image[:, :, 0] == 255) & (image[:, :, 1] == 255) & (image[:, :, 2] == 0)# 计算像素个数
count = np.sum(blue_pixels)print(f"图像中像素值为 (255, 255, 0) 的个数为:{count}")相关文章:

Numpy基础用法
Numpy基础用法 numpy.all()num.sun() numpy.all() numpy 中的 all() 函数用于测试 NumPy 数组中所有元素是否都满足指定条件。它接受一个 NumPy 数组作为输入,并返回一个布尔值,指示数组中所有元素是否都满足条件。让我们通过具体的代码示例来深入探讨 n…...

设计模式--享元模式
享元模式(Flyweight Pattern)是一种结构型设计模式,它通过共享大量细粒度的对象来减少内存消耗。这个模式的核心思想是把对象的状态分为内在状态和外在状态,其中内在状态是可以共享的,而外在状态是需要独立维护的。 享…...

可视化剪辑,账号矩阵,视频分发,聚合私信一体化营销工具 源----代码开发部署方案
可视化剪辑: 为了实现可视化剪辑功能,可以使用流行的视频编辑软件或者开发自己的视频编辑工具。其中,通过设计用户友好的界面,用户可以简单地拖拽和放大缩小视频片段,剪辑出满足需求的视频。在开发过程中,可…...
 100分题解)
CCF-CSP认证考试 202406-2 矩阵重塑(其二) 100分题解
更多 CSP 认证考试题目题解可以前往:CSP-CCF 认证考试真题题解 原题链接: 202406-2 矩阵重塑(其二) 时间限制: 1.0 秒 空间限制: 512 MiB 题目背景 矩阵转置操作是将矩阵的行和列交换的过程。在转置过程…...

初阶数据结构的实现1 顺序表和链表
顺序表和链表 1.线性表1.1顺序表1.1.1静态顺序表(不去实现)1.1.2动态顺序表1.1.2.1 定义程序目标1.1.2.2 设计程序1.1.2.3编写代码1.1.2.3测试和调试代码 1.1.2 顺序表的问题与思考 1.2链表1.2.1链表的概念及结构1.2.1.1 定义程序目标1.2.1.2 设计程序1.…...

破解反爬虫策略 /_guard/auto.js(一) 原理
背景 当用代码或者postman访问一个网站的时候,访问他的任何地址都会返回<script src"/_guard/auto.js"></script>,但是从浏览器中访问显示的页面是正常的,这种就是网站做了反爬虫策略。本文就是带大家来破解这种策略&…...

40.简易频率计(基于等精度测量法)(3)
(1)BCD8421码:十进制数字转换成BCD8421码的方法 补零:你需要显示多少位数字,就在前面补上四倍的位宽。比如你要显示一个十进制8位的数字,就在前面补上8*432个零。判断:判断补零部分显示的十进制…...

关于Centos停更yum无法使用的解决方案
最近在使用Centos7.9系统时候,发现yum仓库无法进行安装软件包了,官方说2024年6月30日进行停更,停更后无法提供对应的软件服务。 我在使用yum安装包的时候发现确实不能使用官方服务了: CentOS停更的影响 CentOS停止更新之后&#…...

插画感言:成都亚恒丰创教育科技有限公司
插画感言:笔触间的灵魂对话 在这个快节奏、高压力的时代,我们时常在寻找那些能够触动心灵、让灵魂得以片刻栖息的角落。而插画,这一融合了艺术与情感的独特形式,便如同一股清泉,缓缓流淌进每个人的心田,以…...

【算法】数组中的第K个最大元素
难度:中等 题目: 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题…...

Perl 语言的特点
Perl 语言入门学习可以涵盖多个方面,包括其特点、基本语法、高级特性以及学习资源和社区支持等。以下是一个详细的入门学习指南: 一、Perl 语言的特点 文本处理能力强:Perl 提供了丰富的字符串处理函数和正则表达式的支持,非常适…...

NLP教程:1 词袋模型和TFIDF模型
文章目录 词袋模型TF-IDF模型词汇表模型 词袋模型 文本特征提取有两个非常重要的模型: 词集模型:单词构成的集合,集合自然每个元素都只有一个,也即词集中的每个单词都只有一个。 词袋模型:在词集的基础上如果一个单词…...

【开源 Mac 工具推荐之 2】洛雪音乐(lx-music-desktop):免费良心的音乐平台
旧版文章:【macOS免费软件推荐】第6期:洛雪音乐 Note:本文在旧版文章的基础上,新更新展示了一些洛雪音乐的新功能,并且描述更为详细。 简介 洛雪音乐(GitHub 名:lx-music-desktop )…...

AMEYA360:思瑞浦推出汽车级理想二极管ORing控制器TPS65R01Q
聚焦高性能模拟芯片和嵌入式处理器的半导体供应商思瑞浦3PEAK(股票代码:688536)发布汽车级理想二极管ORing控制器TPS65R01Q。 TPS65R01Q拥有20mV正向调节功能,降低系统损耗。快速反向关断(Typ:0.39μs),在电池反向和各种汽车电气瞬…...

简约的悬浮动态特效404单页源HTML码
源码介绍 简约的悬浮动态特效404单页源HTML码,页面简约美观,可以做网站错误页或者丢失页面,将下面的代码放到空白的HTML里面,然后上传到服务器里面,设置好重定向即可 效果预览 完整源码 <!DOCTYPE html> <html><head><meta charset="utf-8&q…...

Golang 创建 Excel 文件
经常会遇到需要导出数据报表的需求,除了可以通过 encoding/csv 导出 CSV 以外,还可以使用 https://github.com/qax-os/excelize 导出 xlsx 等格式的 excel,下面封装了一个方法,支持多 sheet 的 excel 数据生成,导出按需…...

探索GitHub上的两个革命性开源项目
在数字世界中,总有一些项目能够以其创新性和实用性脱颖而出,吸引全球开发者的目光。今天,我们将深入探索GitHub上的两个令人惊叹的开源项目:Comic Translate和GPTPDF,它们不仅改变了我们处理信息的方式,还极…...

SpringBoot框架学习笔记(三):Lombok 和 Spring Initailizr
1 Lombok 1.1 Lombok 介绍 (1)Lombok 作用 简化JavaBean开发,可以使用Lombok的注解让代码更加简洁Java项目中,很多没有技术含量又必须存在的代码:POJO的getter/setter/toString;异常处理;I/O…...

【ASP.NET网站传值问题】“object”不包含“GetEnumerator”的公共定义,因此 foreach 语句不能作用于“object”类型的变量等
问题一:不允许遍历 原因:实体未强制转化 后端: ViewData["CateGroupList"] grouplist; 前端加上:var catelist ViewData["CateGroupList"] as List<Catelogue>; 这样就可以遍历catelist了 问题二:…...

Stateflow中的状态转换表
状态转换表是表达顺序模态逻辑的另一种方式。不要在Stateflow图表中以图形方式绘制状态和转换,而是使用状态转换表以表格格式表示模态逻辑。 使用状态转换表的好处包括: 易于对类列车状态机进行建模,其中模态逻辑涉及从一个状态到其邻居的转换…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
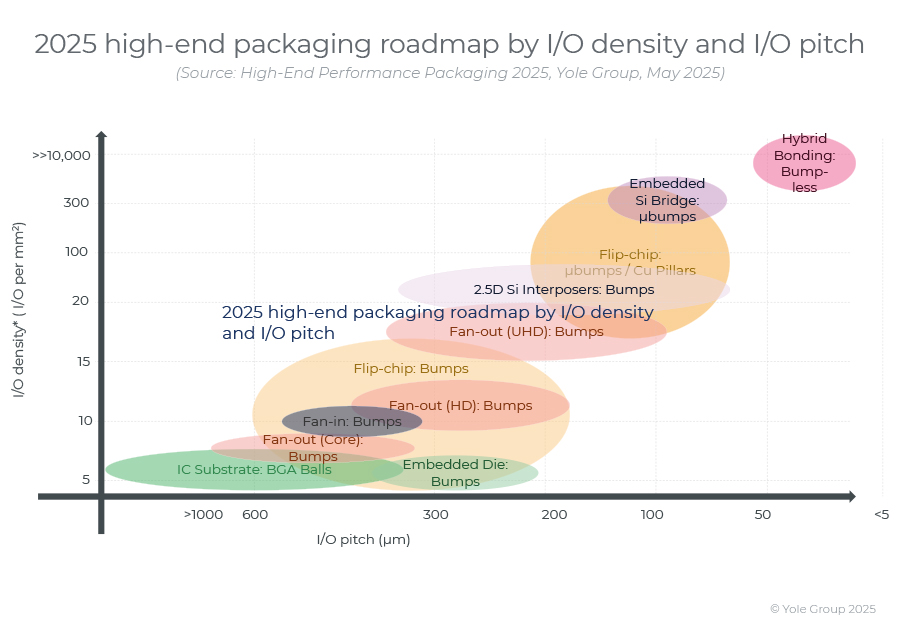
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...

中国政务数据安全建设细化及市场需求分析
(基于新《政务数据共享条例》及相关法规) 一、引言 近年来,中国政府高度重视数字政府建设和数据要素市场化配置改革。《政务数据共享条例》(以下简称“《共享条例》”)的发布,与《中华人民共和国数据安全法》(以下简称“《数据安全法》”)、《中华人民共和国个人信息…...
