【算法】数组中的第K个最大元素
难度:中等
题目:
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 105
-104 <= nums[i] <= 104
解题思路:
要找到数组中第k个最大的元素,且要求时间复杂度为O(n),我们可以使用快速选择算法,这是一种基于快速排序的选择算法变种,用于找到未排序数组中的第k个元素,而无需完全排序数组。
- 选择基准:从数组中随机选择一个元素作为基准元素,或者选择数组的第一个元素、最后一个元素等作为基准。
- 分区操作:将数组分为两部分,一部分包含所有不大于基准的元素,另一部分包含所有大于基准的元素。这个操作结束后,基准元素会处于它在排序后数组中的最终位置。同时,我们也会得到基准元素在排序后数组中的索引。
- 根据基准索引判断:
- 如果基准元素的索引正好是k-1,那么基准元素就是我们要找的第k大的元素。
- 如果基准元素的索引小于k-1,说明第k大的元素在基准的右边,我们在基准的右边数组中继续执行前两步。
- 如果基准元素的索引大于k-1,说明第k大的元素在基准的左边,我们在基准的左边数组中继续执行前两步。
- 递归或迭代:重复上述过程,直到找到第k大的元素。
JavaScript实现:
function findKthLargest(nums, k) {function partition(left, right, pivotIndex) {const pivotValue = nums[pivotIndex];// 将基准元素交换到数组末尾[nums[pivotIndex], nums[right]] = [nums[right], nums[pivotIndex]];let storeIndex = left;for (let i = left; i < right; i++) {if (nums[i] > pivotValue) {[nums[storeIndex], nums[i]] = [nums[i], nums[storeIndex]];storeIndex++;}}// 将基准元素放到正确的位置[nums[right], nums[storeIndex]] = [nums[storeIndex], nums[right]];return storeIndex;}function quickSelect(left, right, kSmallest) {if (left === right) return nums[left];let pivotIndex = Math.floor(Math.random() * (right - left + 1)) + left;pivotIndex = partition(left, right, pivotIndex);if (kSmallest === pivotIndex) {return nums[kSmallest];} else if (kSmallest < pivotIndex) {return quickSelect(left, pivotIndex - 1, kSmallest);} else {return quickSelect(pivotIndex + 1, right, kSmallest);}}// 调整k为基于0的索引return quickSelect(0, nums.length - 1, nums.length - k);
}// 示例
console.log(findKthLargest([3,2,1,5,6,4], 2)); // 输出: 5,因为排序后数组为[1,2,3,4,5,6],第2大的元素是5
这段代码首先定义了partition函数来实现分区操作,然后定义了quickSelect函数来递归地执行快速选择算法。最后,findKthLargest函数调用quickSelect来找到数组中第k大的元素。注意,由于我们是从0开始计数,所以在调用quickSelect时传入的是nums.length - k。
相关文章:

【算法】数组中的第K个最大元素
难度:中等 题目: 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题…...

Perl 语言的特点
Perl 语言入门学习可以涵盖多个方面,包括其特点、基本语法、高级特性以及学习资源和社区支持等。以下是一个详细的入门学习指南: 一、Perl 语言的特点 文本处理能力强:Perl 提供了丰富的字符串处理函数和正则表达式的支持,非常适…...

NLP教程:1 词袋模型和TFIDF模型
文章目录 词袋模型TF-IDF模型词汇表模型 词袋模型 文本特征提取有两个非常重要的模型: 词集模型:单词构成的集合,集合自然每个元素都只有一个,也即词集中的每个单词都只有一个。 词袋模型:在词集的基础上如果一个单词…...

【开源 Mac 工具推荐之 2】洛雪音乐(lx-music-desktop):免费良心的音乐平台
旧版文章:【macOS免费软件推荐】第6期:洛雪音乐 Note:本文在旧版文章的基础上,新更新展示了一些洛雪音乐的新功能,并且描述更为详细。 简介 洛雪音乐(GitHub 名:lx-music-desktop )…...

AMEYA360:思瑞浦推出汽车级理想二极管ORing控制器TPS65R01Q
聚焦高性能模拟芯片和嵌入式处理器的半导体供应商思瑞浦3PEAK(股票代码:688536)发布汽车级理想二极管ORing控制器TPS65R01Q。 TPS65R01Q拥有20mV正向调节功能,降低系统损耗。快速反向关断(Typ:0.39μs),在电池反向和各种汽车电气瞬…...

简约的悬浮动态特效404单页源HTML码
源码介绍 简约的悬浮动态特效404单页源HTML码,页面简约美观,可以做网站错误页或者丢失页面,将下面的代码放到空白的HTML里面,然后上传到服务器里面,设置好重定向即可 效果预览 完整源码 <!DOCTYPE html> <html><head><meta charset="utf-8&q…...

Golang 创建 Excel 文件
经常会遇到需要导出数据报表的需求,除了可以通过 encoding/csv 导出 CSV 以外,还可以使用 https://github.com/qax-os/excelize 导出 xlsx 等格式的 excel,下面封装了一个方法,支持多 sheet 的 excel 数据生成,导出按需…...

探索GitHub上的两个革命性开源项目
在数字世界中,总有一些项目能够以其创新性和实用性脱颖而出,吸引全球开发者的目光。今天,我们将深入探索GitHub上的两个令人惊叹的开源项目:Comic Translate和GPTPDF,它们不仅改变了我们处理信息的方式,还极…...

SpringBoot框架学习笔记(三):Lombok 和 Spring Initailizr
1 Lombok 1.1 Lombok 介绍 (1)Lombok 作用 简化JavaBean开发,可以使用Lombok的注解让代码更加简洁Java项目中,很多没有技术含量又必须存在的代码:POJO的getter/setter/toString;异常处理;I/O…...

【ASP.NET网站传值问题】“object”不包含“GetEnumerator”的公共定义,因此 foreach 语句不能作用于“object”类型的变量等
问题一:不允许遍历 原因:实体未强制转化 后端: ViewData["CateGroupList"] grouplist; 前端加上:var catelist ViewData["CateGroupList"] as List<Catelogue>; 这样就可以遍历catelist了 问题二:…...

Stateflow中的状态转换表
状态转换表是表达顺序模态逻辑的另一种方式。不要在Stateflow图表中以图形方式绘制状态和转换,而是使用状态转换表以表格格式表示模态逻辑。 使用状态转换表的好处包括: 易于对类列车状态机进行建模,其中模态逻辑涉及从一个状态到其邻居的转换…...

结合Redis解决接口幂等性问题
结合Redis解决接口幂等性问题 引言正文收获 引言 该问题产生背景是根据需求描述,要求对已发布的课程能进行编辑修改,并且要求能进行回滚。 幂等性问题描述:对同一个接口并发请求产生的结果是不变的。 Get 请求以及 Delete 请求天然保证幂等…...

2024算力基础设施安全架构设计与思考(免费下载)
算网安全体系是将数据中心集群、算力枢纽、一体化大数据中心三个层级的安全需求进行工程化解耦,从国家安全角度统筹设计,通过安全 服务化方式,依托威胁情报和指挥协同通道将三层四级安全体系串联贯通,达成一体化大数据安全目标。 …...
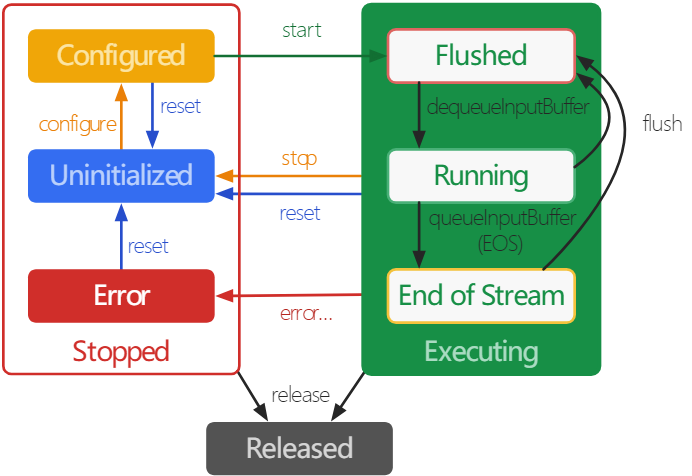
ExoPlayer架构详解与源码分析(15)——Renderer
系列文章目录 ExoPlayer架构详解与源码分析(1)——前言 ExoPlayer架构详解与源码分析(2)——Player ExoPlayer架构详解与源码分析(3)——Timeline ExoPlayer架构详解与源码分析(4)—…...

网络安全-等级保护制度介绍
一、等保发展历程 (1)1994国务院147号令 第一次提出等级保护概念,要求对信息系统分等级进行保护 (2)1999年GB17859 国家强制标准发布,信息系统等级保护必须遵循的法规 (3)2005年公安…...

【介绍下大数据组件之Storm】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
)
React Hook 总结(React 萌新升级打怪中...)
1 useCallback useMemo 和 useCallback 接收的参数都是一样,都是在其依赖项发生变化后才执行,都是返回缓存的值,区别在于 useMemo 返回的是函数运行的结果,useCallback 返回的是函数。 当需要使用 useCallback 的情况通常包括以…...
Typora 1.5.8 版本安装下载教程 (轻量级 Markdown 编辑器),图文步骤详解,免费领取
文章目录 软件介绍软件下载安装步骤激活步骤 软件介绍 Typora是一款基于Markdown语法的轻量级文本编辑器,它的主要目标是为用户提供一个简洁、高效的写作环境。以下是Typora的一些主要特点和功能: 实时预览:Typora支持实时预览功能࿰…...

mac docker no space left on device
mac 上 docker 拉取镜像报错 Error response from daemon: write /var/lib/docker/tmp/docker-export-3995807640/b8464f52498789c4ebbc063d508f04e8d2586567fbffa475e3cd9afd3c5a7cf2/layer.tar: no space left on device解决: 增加 docker 虚拟磁盘大小。如下图...

单片机主控的基本电路
论文 1.复位电路 2.启动模式设置接口 3.VBAT供电接口 4.MCU 基本电路 5.参考电压选择端口...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
