机器学习自学笔记——感知机
感知机预备知识
神经元
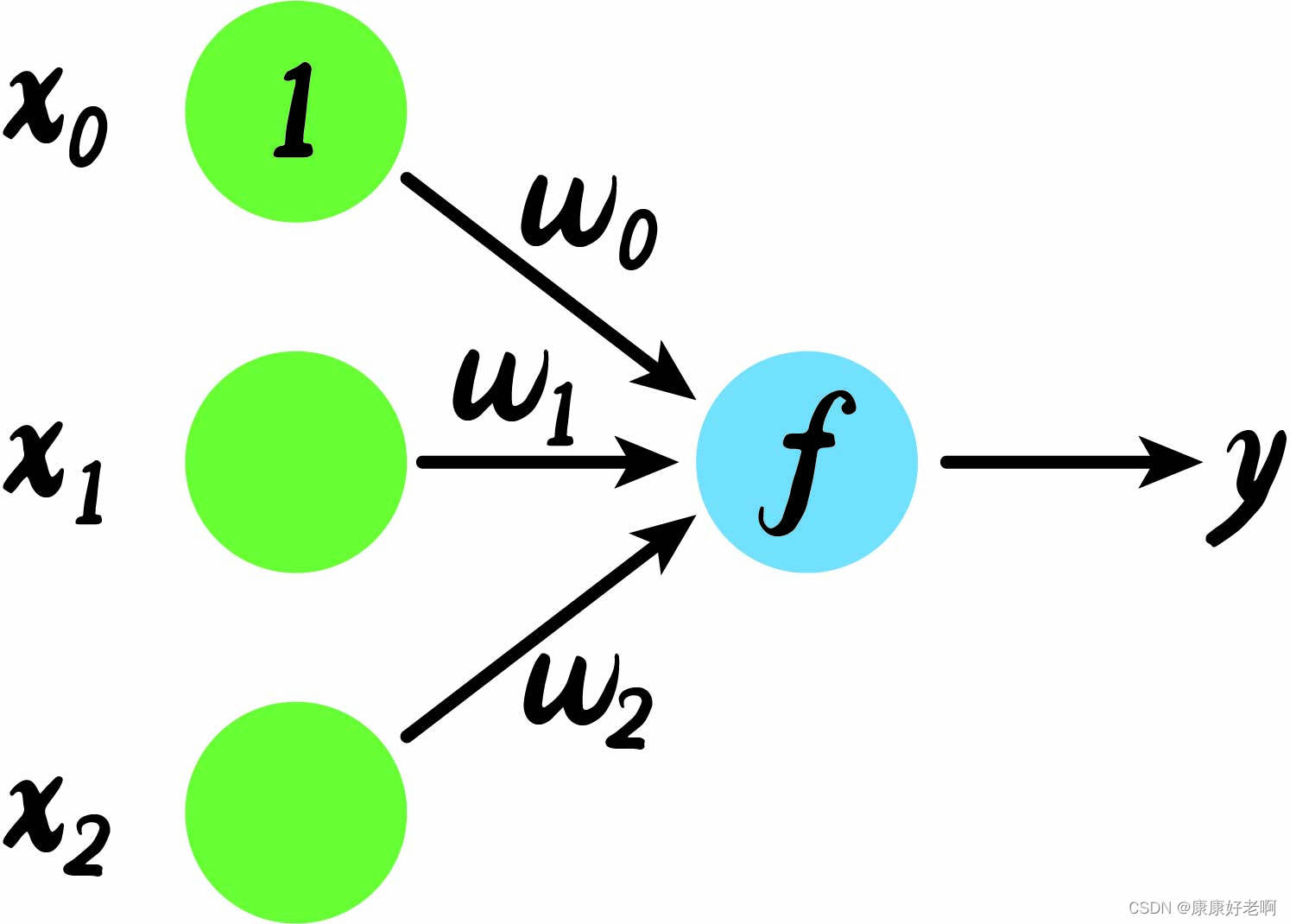
感知机算法最初是由科学家从脑细胞的神经凸起联想而来。如下图,我们拥有三个初始xxx值,x1,x2,x0x_1,x_2,x_0x1,x2,x0。其中x0=1x_0=1x0=1为一个初始的常量,专业上称作“偏置”。每个xxx的值都会乘上一个权重值www,再线性组合生成一个多项式,这个多项式经过一个分类函数fff生成yyy。这个分类函数的作用就是将类别转化成0,10,10,1或者−1,1-1,1−1,1。绿色和蓝色的圆就像是一个个神经元,中间连接www就像是神经元用来传递信号的凸起。
数据集可分性
从直观上理解,数据集可分的概念就是一个数据集可以通过一个超平面将不同的类别的数据样本点完全分开。
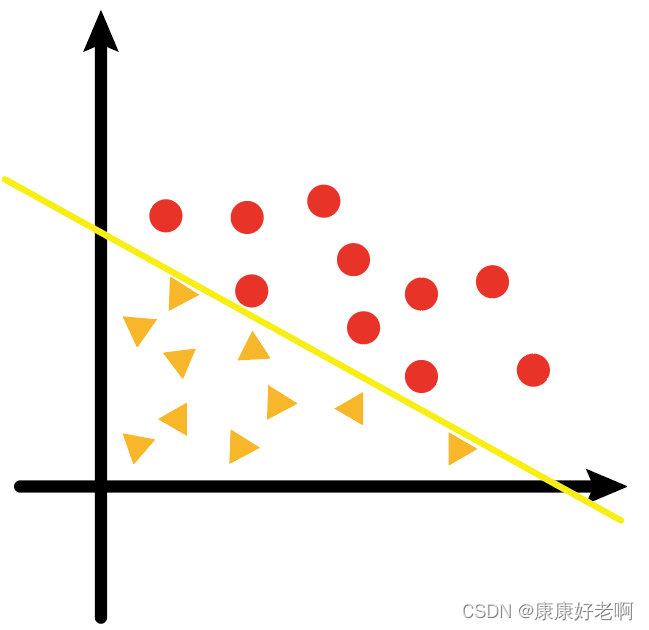
如上图,黄色的线可以将黄色三角形和红色圆形完全分开,不会有黄色三角形在红色圆形的区域,也不会有红色圆形在黄色三角形区域。这样一个数据集就是可分的。
感知机模型
分类函数
重新回到一开始那个图。假设现在我们有一些数据集XXX,有{x10,x20}\{x_{10},x_{20}\}{x10,x20}这两个特征值。我们还有个超平面y=w1x1+w2x2y=w_1x_1+w_2x_2y=w1x1+w2x2。现在我们将这两个特征值输入,会得到下式:
w1x10+w2x20+w0x0=w1x10+w2x20+w0=wTx0+w0w_1x_{10}+w_2x_{20}+w_0x_0=w_1x_{10}+w_2x_{20}+w_0=w^Tx_0+w_0 w1x10+w2x20+w0x0=w1x10+w2x20+w0=wTx0+w0
根据超平面的性质:如果数据点在超平面之上,则wTx0+w0>0w^Tx_0+w_0>0wTx0+w0>0,如果数据点在超平面之下,则wTx0+w0<0w^Tx_0+w_0<0wTx0+w0<0。
根据书写习惯,我们将w0w_0w0换成bbb,单纯换个符号,方便后面区分理解。
但是,对于不同的样本点,其x1,x2x_1,x_2x1,x2值不相同,所计算出来的wTx+bw^Tx+bwTx+b肯定也不相同。那我们如何去区分这两个类别呢?
最直观的一种想法就是,让不同的类别对应其特殊的一个常数,比如类别1对应的是0,类别2对应的是1。这就涉及到一个问题,就是要将之前wTx+bw^Tx+bwTx+b的值转化成0和1。而这一步就是fff的作用了。
fff称为激活函数,就是将wTx+bw^Tx+bwTx+b转化成0,1。激活函数有很多,我们这使用的是sign函数:
sign(x)={+1,x>0−1,x<0sign(x)=\begin{cases} +1,&x>0\\ -1,&x<0 \end{cases} sign(x)={+1,−1,x>0x<0
在上面我们提到超平面的性质,如果点在超平面之上,那么wTx+b>0w^Tx+b>0wTx+b>0,此时正好对应sign函数中的+1,点在超平面之下同理。这也是为什么sign函数能达到分类的目的。于是我们得到感知机的分类函数:
yi=sign(wTx0+b)y_i=sign(w^Tx_0+b) yi=sign(wTx0+b)
损失函数
在模型训练的过程中,仅仅有一个分类函数是远远不够的。我们需要有一个损失函数,用来不断优化分类函数中www的权重值。
我们或许可以直接想到,误分类点个数可以作为损失函数的标准:误分类点数目越少,分类越准确。但是这有两个问题:
- 第一个是即使拥有相同的误分类点数目,误分类点距离超平面远近不同,其分类效果也是不一样的。
- 第二个是将误分类点个数作为损失函数难以进行优化。我们知道要减少误分类点的个数,但是具体怎么减少,函数里没有体现。
上面两个问题我们可以通过如下方式进行解决:
首先第一个问题,损失函数需要能够衡量误分类点距离超平面的远近距离。已知点到直线的距离公式为:
d=∣wTx0+b∣∣∣w∣∣d=\frac{|w^Tx_0+b|}{||w||} d=∣∣w∣∣∣wTx0+b∣
对于同一条直线,∣∣w∣∣||w||∣∣w∣∣是不会发生变化的,所以可以省去。此外我们可以考虑下误分类点的状况:
- 当超平面上方的点误分类到下方时,所以wTx+b<0w^Tx+b<0wTx+b<0,但是实际上正确的分类yi=+1y_i=+1yi=+1;
- 当超平面下方的点误分类到上方时,所以wTx+b>0w^Tx+b>0wTx+b>0,但是实际上正确的分类yi=−1y_i=-1yi=−1;
无论是哪一种情况,都满足yi(wTx+b)<0y_i(w^Tx+b)<0yi(wTx+b)<0。所以如果我们使用−yi(wTx+b)-y_i(w^Tx+b)−yi(wTx+b)作为损失函数就可以解决第一个问题,而第二个问题也可以顺便解决。由于要考虑到是多个误分类点,所以我们还要加上∑\sum∑。
这里之所以要填符号是因为我们希望损失函数越小,超平面分类越准确。
所以分类函数为:
L(wi,w0)=−∑xi∈Myi(wTx+b)L(w_i,w_0)=-\sum_{x_i∈M}y_i(w^Tx+b) L(wi,w0)=−xi∈M∑yi(wTx+b)
参数更新
有了损失函数之后,我们就可以通过梯度下降进行参数更新,不断优化使分离超平面分类更加准确。
根据梯度下降算法,我们需要对损失函数求偏导:
∇wL(wiT,b)=−∑xi∈Myixi∇bL(wiT,b)=−∑xi∈Myi\nabla_wL(w^T_i,b)=-\sum_{x_i∈M}y_ix_i \\\nabla_bL(w^T_i,b)=-\sum_{x_i∈M}y_i ∇wL(wiT,b)=−xi∈M∑yixi∇bL(wiT,b)=−xi∈M∑yi
然后就可以进行参数更新了:
wT→wT+ηyixib→b+ηyiw^T\to w^T+\eta y_ix_i \\b\to b+\eta y_i wT→wT+ηyixib→b+ηyi
其中η\etaη为学习率。
感知机算法的原始形式
所以我们得到了感知机算法:
-
输入:训练集TTT,学习率η\etaη
-
输出:wT,bw^T,bwT,b
感知机模型: f(x)=sign(wT∗x+b)f(x)=sign(w^T∗x+b)f(x)=sign(wT∗x+b)
步骤流程:
(1) 初始化 w0,b0w_0,b_0w0,b0。
(2) 在训练集中选取数据 (xi,yi)(x_i,y_i)(xi,yi)
(3) 若 yi(wT∗xi+b)≤0y_i(w^T∗x_i+b)≤0yi(wT∗xi+b)≤0 (误分类点),则进行参数更新:
wT→w+ηyixiw^T\to w+ηy_ix_iwT→w+ηyixi
bT→b+ηyib^T\to b+ηy_ibT→b+ηyi
(4) 转至(2),直到训练集没有误分类点。
对偶问题
上面我们提到,利用梯度下降进行参数更新:
wT→wT+ηyixib→b+ηyiw^T\to w^T+\eta y_ix_i \\b\to b+\eta y_i wT→wT+ηyixib→b+ηyi
如果我们假设样本点(xi,yi)(x_i,y_i)(xi,yi)在更新过程中被使用了nin_ini次,也就是进行了nin_ini次迭代,所以我们可以得到wT和bw^T和bwT和b的表达式。
wT=∑i=1Nniηyixib=∑i=1Nniηyiw^T=\sum_{i=1}^N n_i\eta y_ix_i \\b=\sum_{i=1}^N n_i\eta y_i wT=i=1∑Nniηyixib=i=1∑Nniηyi
将其代入到原始感知机模型当中,
f(x)=sign(wT∗x+b)=sign(∑i=1Nniηyixi⋅x+∑i=1Nniηyi)f(x)=sign(w^T∗x+b)=sign(\sum_{i=1}^N n_i\eta y_ix_i·x+\sum_{i=1}^N n_i\eta y_i) f(x)=sign(wT∗x+b)=sign(i=1∑Nniηyixi⋅x+i=1∑Nniηyi)
此时学习目标就是nin_ini
感知机算法的对偶形式
-
输入:训练集TTT,学习率η\etaη
-
输出:nin_ini
感知机模型: f(x)=sign(∑i=1Nniηyixi⋅x+∑i=1Nniηyi)f(x)=sign(\sum_{i=1}^N n_i\eta y_ix_i·x+\sum_{i=1}^N n_i\eta y_i)f(x)=sign(∑i=1Nniηyixi⋅x+∑i=1Nniηyi)
步骤流程:
(1) 初始化 $n_i $。
(2) 在训练集中选取数据 (xi,yi)(x_i,y_i)(xi,yi)
(3) 若 yi(∑i=1Nniηyixi⋅x+∑i=1Nniηyi)≤0y_i(\sum_{i=1}^N n_i\eta y_ix_i·x+\sum_{i=1}^N n_i\eta y_i)≤0yi(∑i=1Nniηyixi⋅x+∑i=1Nniηyi)≤0 (误分类点),则进行参数更新:
ni→ni+1n_i\to n_i+1ni→ni+1
(4) 转至(2),直到训练集没有误分类点。
也有另外一种写法:
-
输入:训练集TTT,学习率η\etaη
-
输出:αi,b\alpha_i,bαi,b(αi=niη\alpha_i=n_i\etaαi=niη)
感知机模型: f(x)=sign(∑i=1Nαiyixi⋅x+b)f(x)=sign(\sum_{i=1}^N\alpha_i y_ix_i·x+b)f(x)=sign(∑i=1Nαiyixi⋅x+b)
步骤流程:
(1) 初始化 nin_ini。
(2) 在训练集中选取数据 (xi,yi)(x_i,y_i)(xi,yi)
(3) 若 yi(∑i=1Nniηyixi⋅x+b)≤0y_i(\sum_{i=1}^N n_i\eta y_ix_i·x+b)≤0yi(∑i=1Nniηyixi⋅x+b)≤0 (误分类点),则进行参数更新:
αi→αi+η\alpha_i\to \alpha_i+\etaαi→αi+η
b→b+ηyib\to b+\eta y_ib→b+ηyi
(4) 转至(2),直到训练集没有误分类点。
相关文章:

机器学习自学笔记——感知机
感知机预备知识 神经元 感知机算法最初是由科学家从脑细胞的神经凸起联想而来。如下图,我们拥有三个初始xxx值,x1,x2,x0x_1,x_2,x_0x1,x2,x0。其中x01x_01x01为一个初始的常量,专业上称作“偏置”。每个xxx的值都会乘上一个权重…...
)
C++ Primer第五版_第三章习题答案(21~30)
文章目录练习3.21练习3.22练习3.23练习3.24练习3.25练习3.26练习3.27练习3.28练习3.29练习3.30练习3.21 请使用迭代器重做3.3.3节的第一个练习。 #include <vector> #include <iterator> #include <string> #include <iostream>using std::vector; usi…...

colmap+openmvs进行三维重建流程全记录
window下的colmapopenmvs进行三维重建流程全记录 1.colmap安装与配置 可参考:https://blog.csdn.net/weixin_44153180/article/details/129334018?spm1001.2014.3001.5501 2.openmvs安装与配置 可参考:https://blog.csdn.net/rdw1246010462/article…...

yolov8命令行运行参数详解
序言 整理来自yolov8官方文档常用的一些命令行参数,官方文档YOLOv8 Docs yolov8命令行的统一运行格式为: yolo TASK MODE ARGS其中主要是三部分传参: TASK(可选) 是[detect、segment、classification]中的一个。如果没有显式传递…...

分布式锁简介
Redis因为单进程、性能高常被用于分布式锁;锁在程序中作用是同步工具,保证共享资源在同一时刻只能被一个线程访问。 Java中经常用的锁synchronized、Lock,但是Java的锁智能保证单机的时候有效,分布式集群环境就无能为力了…...

【嵌入式Linux学习笔记】Linux驱动开发
Linux系统构建完成后,就可以基于该环境方便地进行开发了,相关的开发流程与MCU类似,但是引入了设备树的概念,编写应用代码要相对复杂一点。但是省去了很多配置工作。 学习视频地址:【正点原子】STM32MP157开发板 字符…...
上海理工大学校内选拔赛(同步赛)(H题)(线段树))
2023年中国高校计算机大赛-团队程序设计天梯赛(GPLT)上海理工大学校内选拔赛(同步赛)(H题)(线段树)
又到了万物复苏的季节,家乡的苹果树结果了。像往常一样小龙同学被叫回家摘苹果。 假设需要采摘的一棵树上当前有a颗苹果,那么小龙会采摘⌈a/3⌉颗苹果,其中⌈x⌉表示不小于x的最小整数。 但是,为了可持续发展,若a小于1…...
)
Linux内核Thermal框架详解十三、Thermal Governor(3)
接前一篇文章Linux内核Thermal框架详解十二、Thermal Governor(2) 二、具体温控策略 上一篇文章介绍并详细分析了bang_bang governor的源码。本文介绍第2种温控策略:fair_share。 2. fair_share fair_share governor总的策略是频率档位⽐较…...
)
TikTok品牌出海创世纪(二)
目录 1.推荐算法打造王者品牌 2.品牌聚焦海外Z群体 3.持续扩展应用场景 加速品牌全球化传播 品牌聚焦海外Z群体 “这个地球上,三分之二的人都在用Facebook“,这是对Facebook曾经统治地位最直观的描述。 但如今,这家全球社交媒体巨头的光环正…...
iOS中SDK开发 -- cocoapods库创建
在iOS项目中,经常使用cocoadpods来进行依赖管理以及三方库引入等。引入的三方库一般会有几种形式:一、在Pods目录下可以直接看到源代码的开源库,如AFNetworking,Masonry等常见开源库。二、在Pods目录下拉取的项目文件只能看到对应…...

2023年了,还是没学会内卷....
先做个自我介绍:我,普本,通信工程专业,现在飞猪干软件测试,工作时长两年半。 回望疫情纪元,正好是实习 毕业这三年。要说倒霉也是真倒霉,互联网浪潮第三波尾巴也没抓住,狗屁造富神…...

chatGPT爆火,什么时候中国能有自己的“ChatGPT“
目录 引言 一、ChatGPT爆火 二、中国何时能有自己的"ChatGPT" 三、为什么openai可以做出chatGPT? 四、结论 引言 随着人工智能技术的不断发展,自然语言处理技术也逐渐成为了研究的热点之一。其中,ChatGPT作为一项领先的自然语言处理技术…...
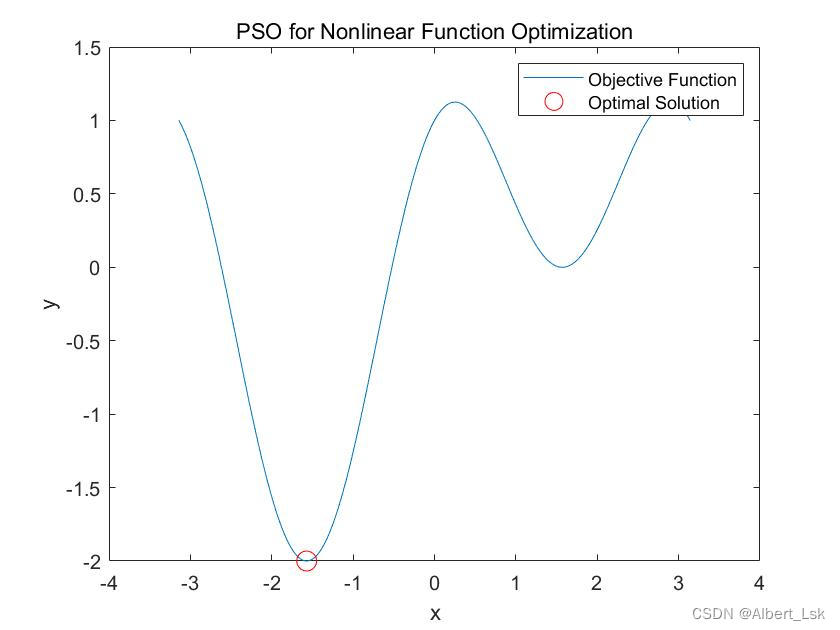
【Matlab算法】粒子群算法求解一维非线性函数问题(附MATLAB代码)
MATLAB求解一维非线性函数问题前言正文函数实现(可视化处理)可视化结果前言 一维非线性函数是指函数的自变量和因变量都是一维实数,而且函数的形式是非线性的,也就是不符合线性函数的形式。在一维非线性函数中,自变量…...

2023 最新发布超全的 Java 面试八股文,整整 1000道面试题,太全了
作为一名优秀的程序员,技术面试都是不可避免的一个环节,一般技术面试官都会通过自己的方式去考察程序员的技术功底与基础理论知识。 2023 年的互联网行业竞争越来越严峻,面试也是越来越难,很多粉丝朋友私信希望我出一篇面试专题或…...

产品经理面经|当面试官问你还有什么问题?
相信很多产品经理在跳槽面试的时候,在面试尾声都会遇到这样的环节,面试官会问你有什么问题要问的,一般来说大家都能随时随地甩出几个问题来化解,但其实在这个环节对于应聘者来说也是一个很好的机会来展现自己的能力,甚…...

单链表的基本操作
目录 一.链表的基本概念和结构 二.链表的分类 三.单链表的基本操作 1.创建一个节点 2.打印 3.尾插 4.头插 5.尾删 6.头删 7.查找 8.指定位置插入 9.指定位置删除 10.销毁 一.链表的基本概念和结构 概念:链表是一种物理存储结构上非连续、非顺序的存储结…...
)
【微信小程序-原生开发】系列教程目录(已完结)
01-注册登录账号,获取 AppID、下载安装开发工具、创建项目、上传体验 https://sunshinehu.blog.csdn.net/article/details/128663679 02-添加全局页面配置、页面、底部导航 https://sunshinehu.blog.csdn.net/article/details/128705866 03-自定义底部导航&#x…...

JavaEE--Thread 类的基本用法(不看你会后悔的嘿嘿)
Thread类是JVM用来管理线程的一个类,换句话说,每个线程都唯一对应着一个Thread对象. 因此,认识和掌握Thread类弥足重要. 本文将从 线程创建线程中断线程等待线程休眠获取线程实例 等方面来进行具体说明. 1)线程创建 方法1:通过创建Thread类的子类并重写run () 方法 class M…...

MySQL数据库基本使用(二)-------数据库及表的增删改查及字符集修改
1.MySQL数据库的使用演示 1.1创建自己的数据库 命令格式如下(创建的数据库名称不能与已经存在的数据库重名): mysql> create database 数据库名;例如: mysql> create database atguigudb; #创建atguigudb数据库…...
)
互联网摸鱼日报(2023-03-17)
互联网摸鱼日报(2023-03-17) InfoQ 热门话题 开源新生代的成长之路:从校园到开源,需要迈过哪些挑战? 从 Clickhouse 到 Apache Doris,慧策电商 SaaS 高并发数据服务的改造实践 刚刚,百度文心…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
