给定一整数数组,其中有p种数出现了奇数次,其他数都出现了偶数次,怎么找到这p个数?
给定一长度为m的整数数组
,其中有p种不为0的数出现了奇数次,其他数都出现了偶数次,找到这p个数。
要求:时间复杂度不大于O(n),空间复杂度不大于O(1)。
由于时间复杂度不大于O(n),则不能在遍历数组中嵌套遍历数组。而空间复杂度不大于O(1),则不能开辟数量上优势或等势于数组长度的内存空间。这需要将数组元素的信息压缩到一个有限的内存空间里,因此需要按位运算。
按位异或运算⊕是具有如下性质的二元运算:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0,并且满足交换率、结合率。则0是⊕的单位元,即对于任意的二进制数a,都有a⊕0=0⊕a=a。而且a与自身互为逆元,即a⊕a=0。记
那么,对于任意正整数k,有:
对于给定的这个题目,当p=1时,设出现了2k+1次,其余的数都出现偶数次,则根据上述的结论有:
即将A中所有元素取异或运算即是此问题的解。
当p=2时,取,则必然b≠0,否则可以推出这两个数相等,从而产生悖论。取
,s为c的二进制表示中从后数第一个为1的位数。
遍历集合A,使每个元素都和c做按位与运算,结果只能是0或者c。取结果为c的元素组成子集A',由于b的第s位是1,则两个目标数字不会都是A'的元素,否则经过⊕运算,s位的值是0的话,如果b中没有某位是1的数字,则b=0,从而产生矛盾。这样,就将问题转化成了在集合A'中查找只有一种非零整数出现奇数次的问题。即求出为其中的一个解。
由于,所以
就是另一个解。
当时,
可能不为0,也可能为0。比如
,整体取二进制按位异或就是
.所以当
时需要对问题进行降阶拆解:
continuing
相关文章:
给定一整数数组,其中有p种数出现了奇数次,其他数都出现了偶数次,怎么找到这p个数?
给定一长度为m的整数数组 ,其中有p种不为0的数出现了奇数次,其他数都出现了偶数次,找到这p个数。 要求:时间复杂度不大于O(n),空间复杂度不大于O(1)。 由于时间复杂度不大于O(n),则不能在遍历数组中嵌套遍…...

RICHTEK立锜科技 WIFI 7电源参考设计
什么是WIFI 7? WiFi 7(Wi-Fi 7)是下一代Wi-Fi标准,对应的是IEEE 802.11将发布新的修订标准IEEE 802.11be –极高吞吐量EHT(Extremely High Throughput )。Wi-Fi 7是在Wi-Fi 6的基础上引入了320MHz带宽、4096-QAM、Mu…...

CUDA编程00 - 配置CUDA开发环境
第一步: 在一台装有Nvidia显卡和驱动的机器上,用nvidia-smi命令查看显卡所支持cuda版本 第二步: 到Nvidia官网下载CUDA Toolkit并安装,CUDA Toolkit Archive | NVIDIA Developer 安装时按提示下一步即可,安装完成用 …...

HTML5大作业三农有机,农产品,农庄,农旅网站源码
文章目录 1.设计来源1.1 轮播图页面头部效果1.2 栏目列表页面效果1.3 页面底部导航效果 2.效果和源码2.1 源代码 源码下载万套模板,程序开发,在线开发,在线沟通 作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_4…...
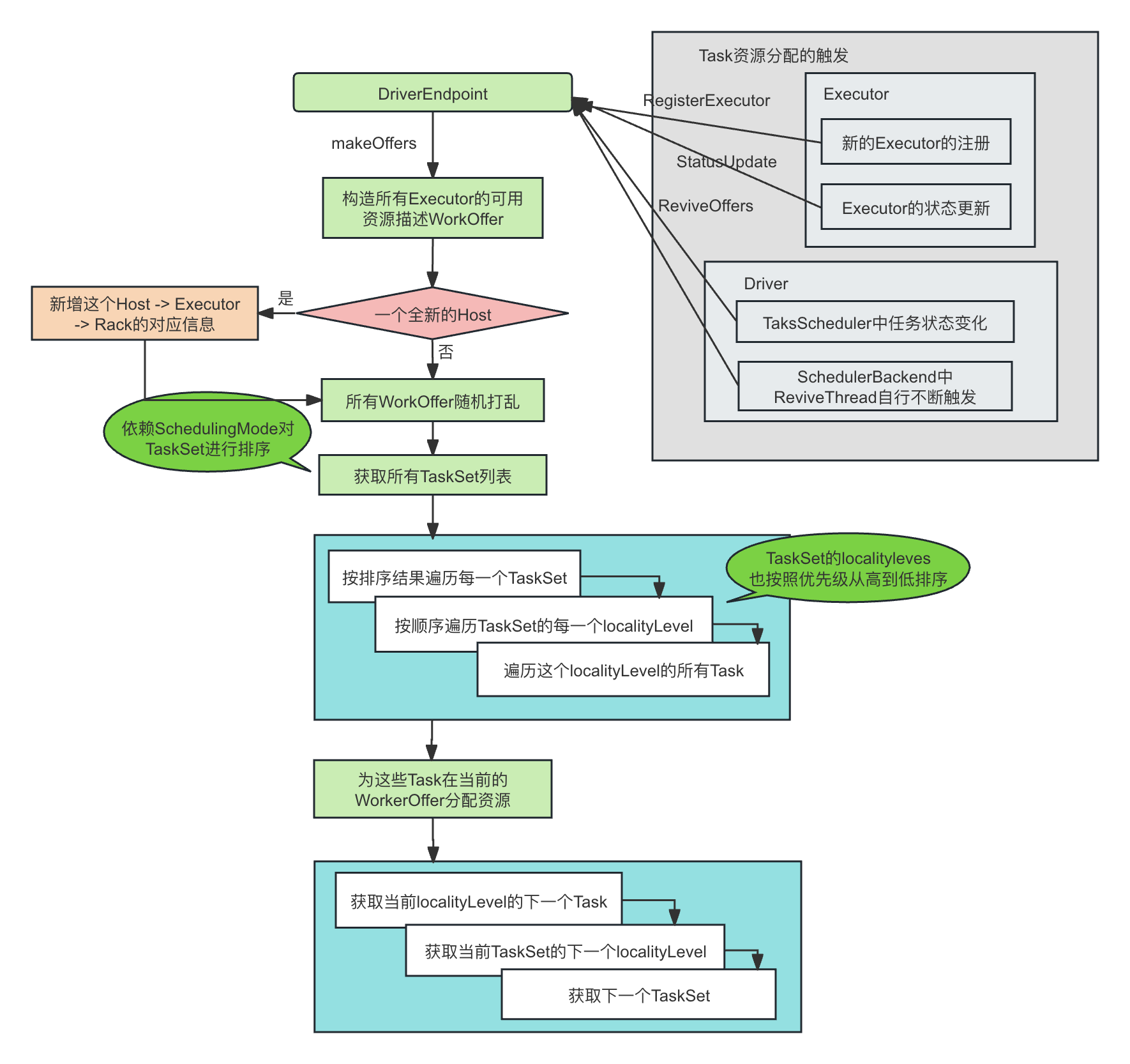
Spark的动态资源分配算法
文章目录 前言基于任务需求进行资源请求的整体过程资源申请的生成过程详解资源申请的生成过程的简单例子资源调度算法的代码解析 申请资源以后的处理:Executor的启动或者结束对于新启动的Container的处理对于结束的Container的处理 基于资源分配结果进行任务调度Pen…...

Python 爬虫技术 第06节 HTTP协议与Web基础知识
HTTP(Hypertext Transfer Protocol)是用于从Web服务器传输超文本到本地浏览器的传输协议。它是互联网上应用最为广泛的一种网络协议,几乎所有的网页数据都是通过HTTP协议进行传输的。下面,我将结合一个简单的Python案例来详细讲解…...

js | 原型链
为什么前者会输出Lucas 后者不会?call动作具体干了什么? http://dmitrysoshnikov.com/ecmascript/javascript-the-core/ function Foo(){this.bar"Lucas" } let obj{}; obj.__proto__Foo.prototype; Foo.call(obj) console.log(obj.bar); // 输出Lucas/…...
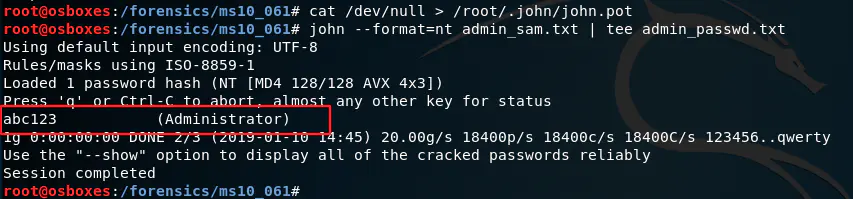
Volatility:分析MS10-061攻击
1、概述 # 1)什么是 Volatility Volatility是开源的Windows,Linux,MaC,Android的内存取证分析工具。基于Python开发而成,可以分析内存中的各种数据。Volatility支持对32位或64位Wnidows、Linux、Mac、Android操作系统…...

水表数字识别3:Pytorch CRNN实现水表数字识别(含训练代码和数据集)
水表数字识别3:Pytorch CRNN实现水表数字识别(含训练代码和数据集) 目录 水表数字识别3:Pytorch CRNN实现水表数字识别(含训练代码和数据集) 1.前言 2. 水表数字识别的方法 3. 水表数字识别数据集 4. 水表数字分割模型训练 5. 水表数字识别模型训…...

oracle数据文件损坏和误删dbf文件处理方法
加油,新时代打工人! 打开sqlplus sqlplus> “/as sysdba” (命令行登录sqlplus) SQL>shutdown abort; (关闭oracle数据库服务器) SQL>startup mount ;(挂载oracle数据库,这…...
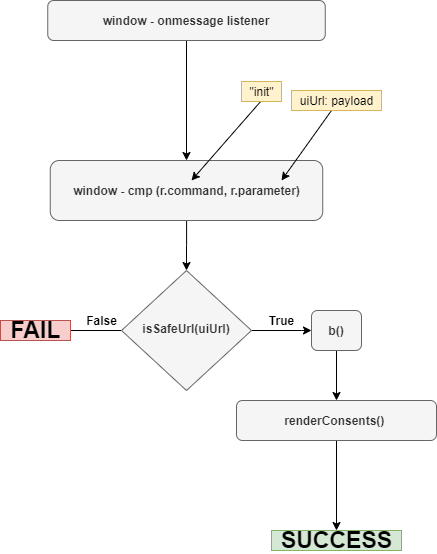
postMessageXss续2
原文地址如下:https://research.securitum.com/art-of-bug-bounty-a-way-from-js-file-analysis-to-xss/ 在19年我写了一篇文章,是基于postMessageXss漏洞的入门教学:https://www.cnblogs.com/piaomiaohongchen/p/14727871.html 这几天浏览mXss技术的时候ÿ…...

【深度学习】sdxl的Lora训练技巧
在进行SDXL LoRA训练时,有一些技巧和最佳实践可以帮助你获得更好的结果。以下是一些重要的建议: 图像选择与标注: 选择多样化的高质量图像是关键,建议至少使用30到50张分辨率为1024x1024的图像【8†source】【9†source】。使用Vi…...
推荐一款 Android 手机端的 SSH 远程连接工具
https://andi.cn/page/621590.html...

3.1、matlab双目相机标定实验
1、双目相机标定原理及流程 双目相机标定是将双目相机系统的内外参数计算出来,从而实现双目视觉中的立体测量和深度感知。标定的目的是确定各个摄像头的内部参数(如焦距、主点、畸变等)和外部参数(如相机位置、朝向等),以便将双目相机捕获的图像转换为三维空间坐标。 双…...

IntelliJ IDEA 直接在软件中更新为最新版
当我们的 IDEA 工具许久没有更新,已经拖了好几个版本,想跨大版本更新,比如从2020.2.1 -> 2023.x.x 此时,我们菜单栏点击 Help -> Check for Updates… ,右下角会有提示更新,如下图: 点…...

库卡机器人示教器 KPC2 00107-264 KPC200.107-264
库卡驱动器是一种高性能的控制器,其作用类似于变频器在普通交流马达中的应用。它通过位置、速度和力矩三种方式对伺服马达进行控制,以满足各种高精度定位系统的需求。库卡驱动器是伺服系统的重要组成部分,广泛应用于各种工业自动化领域。 库…...

数据传输安全--VPN
目录 前置知识 VPN概念 VPN诞生的原因 VPN分类 根据建设的单位不同分类 企业自建的VPN 运营商搭建的VPN 根据组网方式不同来进行分类 Client to LAN VPN LAN to LAN VPN按层次划分 VPN常用技术 VPN的核心技术 VPN封装过程的角色 VPN包含的技术 身份认证技术 加…...

【人工智能】人工智能可解释性和透明度的详细探讨
人工智能的可解释性和透明度是当前AI领域的重要议题,它们对于AI系统的公正性、可靠性、用户信任以及合规性等方面都具有深远的影响。以下是对人工智能可解释性和透明度的详细探讨: 一、人工智能的可解释性 定义: 可解释性是指机器学习模型…...

vscode+wsl2+anaconda环境的配置与使用
目录 下载anaconda Anaconda使用参考 vscodeubuntuanaconda 先用vscode连接本地ubuntu。 如果没有安装wsl2与ubuntu,可点击下面的链接。 问题:wsl install 无法解析服务器 成功记录: 在vscode终端用ubuntu安装anaconda。 创建pytho…...

【Linux网络】套接字编程
本篇博客整理了 socket 套接字编程的相关内容,包括 socket 网络通信原理、socket 相关的系统调用接口等,分别演示了基于UDP协议、TCP协议的 socket 网络编程,旨在让读者更加深入理解网络通信原理和设计,对网络编程有初步的认识和掌…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
