BUG ImportError: cannot import name ‘QAction‘ from ‘PySide6.QtWidgets‘
BUG ImportError: cannot import name ‘QAction’ from ‘PySide6.QtWidgets’
环境
PySide6 6.7.2
详情
在参考 PyQt5 的代码写 Pyside6 的右键菜单时遇到的错误。
错误代码
from PySide6.QtWidgets import QAction
错误原因:
在PySdie6中,QtWidgets模块并不包含这个QAction类,QAction实际上位于PySide6.QtGui模块下。
这是PySide6和PyQt5的不同点之一。
解决方法
改为从PySide6.QtGui模块导入
from PySide6.QtGui import QAction
相关文章:

BUG ImportError: cannot import name ‘QAction‘ from ‘PySide6.QtWidgets‘
BUG ImportError: cannot import name ‘QAction’ from ‘PySide6.QtWidgets’ 环境 PySide6 6.7.2详情 在参考 PyQt5 的代码写 Pyside6 的右键菜单时遇到的错误。 错误代码 from PySide6.QtWidgets import QAction错误原因: 在PySdie6中…...

对某次应急响应中webshell的分析
文章前言 在之前处理一起应急事件时发现攻击者在WEB应用目录下上传了webshell,但是webshell似乎使用了某种加密混淆手法,无法直观的看到其中的木马连接密码,而客户非要让我们连接webshell来证实此文件为后门文件且可执行和利用(也是很恼火&a…...

Vue3新特性
Vue3新特性 1、Composition API1.1 什么是 Composition API1.2 常用 Composition API1.2.1 setup1.2.2 ref1.2.3 reactive1.2.4 computed1.2.5 watchEffect、watchPostEffect、watchSyncEffect1.2.6 watch 2、生命周期2.1 Vue3生命周期钩子2.2 vue2 和 vue3 关于生命周期的对比…...

一套功能齐全、二开友好的即时通讯IM工具,提供能力库和UI库,支持单聊、频道和机器人(附源码)
前言 在当今数字化时代,即时通讯(IM)和实时音视频(RTC)功能已成为众多应用的标配。然而,现有的解-决方案往往存在一些痛点,如架构落后、成本高昂、数据安全性和隐私保护不足,以及二次开发和部署的复杂性。 为了解决这些问题&…...

MySQL:JOIN 多表查询
多表查询 在关系型数据库中,表与表之间是有联系的,它们通过 外键 联系在一起,所以在实际应用中,经常使用多表查询。多表查询就是同时查询两个或两个以上的表。 MySQL多表查询是数据库操作中非常重要的一部分,它允许你…...

【机器学习】必会算法模型之:一文掌握 密度聚类,建议收藏。
密度聚类 1、引言2、密度聚类2.1 定义2.2 核心原理2.3 实现步骤2.4 算法公式2.5 代码示例 3、总结 1、引言 在机器学习的无监督学习领域,聚类是一项基础而重要的任务。 聚类算法通过将数据点分组,使同一组内的数据点具有更大的相似性,而组间…...
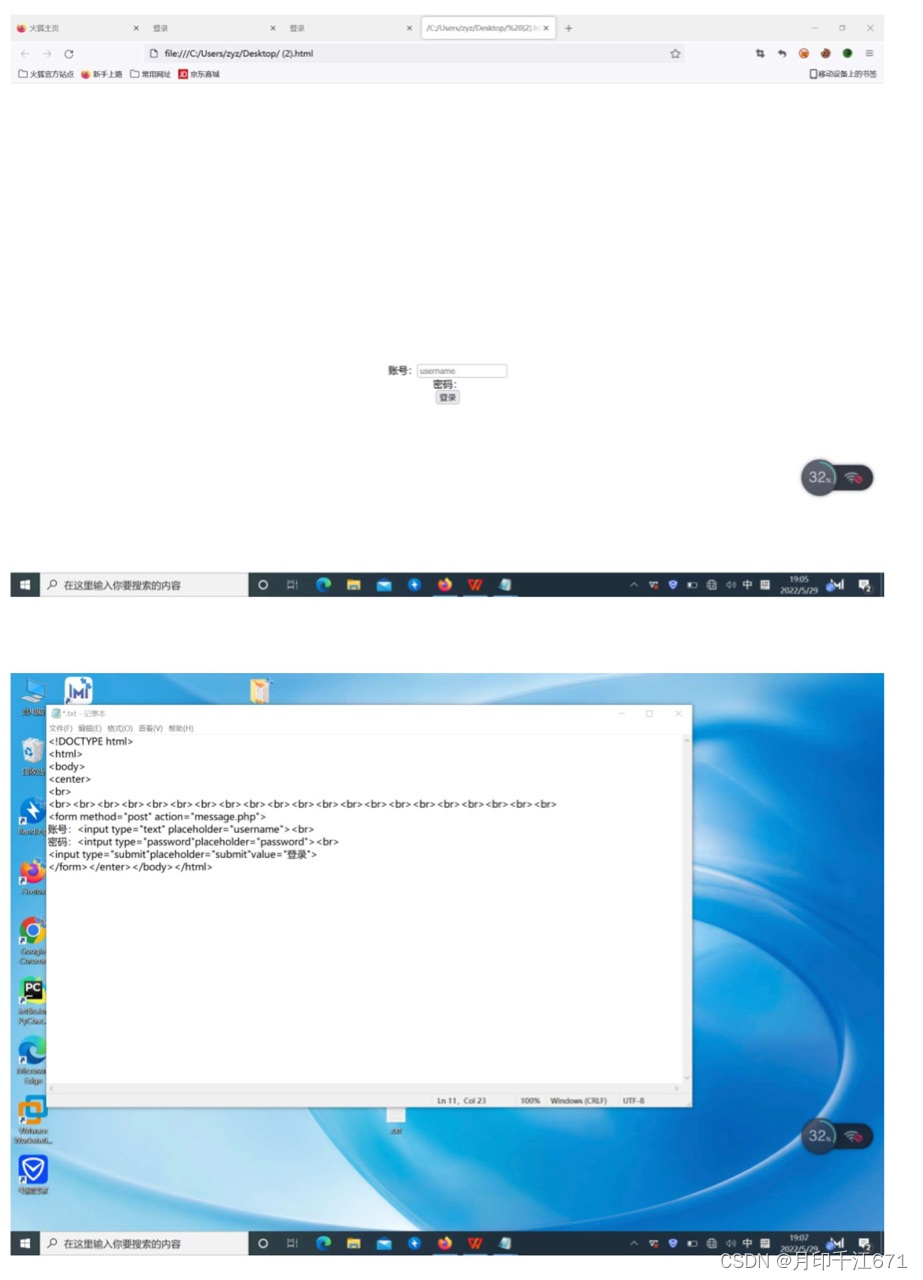
代码:前端与数据库交互的登陆界面
<!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>登录</title> </head> <body>…...

发电机基础知识:负载组
什么是发电机负载组? 简单地说,负载组是一种可以产生人工电力负载的设备,用于测试发电机并验证发电机组的性能,包括相关组件,以确保通过使发电机发动机达到适当的工作温度和压力来满足适当的负载。 它是如何工作的&a…...

内网安全:各类密码的抓取
Mimikatz在线读取SAM文件 离线读取SAM文件 在线读取lsass进程 离线读取lsass进程 BrowserGhost浏览器密码抓取 Sharp-HackBrowserData浏览器密码抓取 SharpDecryptPwd数据库密码抓取 LaZagne各类密码的抓取 Windows其他类型抓NTLM Hash工具 sam文件和lsass进程就是Wind…...

前端面试题汇总2
1. CSS 中两个 .class1 .class2 从哪个开始解析 在 CSS 中,选择器 .class1 .class2 表示所有 class 为 class1 的元素中的 class 为 class2 的子元素。浏览器解析这个选择器时,从右向左解析。也就是说,浏览器首先找到所有 class 为 class2 的…...

分布式服务框架zookeeper+消息队列kafka
一、zookeeper概述 zookeeper是一个分布式服务框架,它主要是用来解决分布式应用中经常遇到的一些数据管理问题,如:命名服务,状态同步,配置中心,集群管理等。 在分布式环境下,经常需要对应用/服…...

服务攻防-应用协议cve
Cve-2015-3306 背景: ProFTPD 1.3.5中的mod_copy模块允许远程攻击者通过站点cpfr和site cpto命令读取和写入任意文件。 任何未经身份验证的客户端都可以利用这些命令将文件从文件系统的任何部分复制到选定的目标。 复制命令使用ProFTPD服务的权限执行,…...

Springcloud之gateway的使用详解
官网地址:https://docs.spring.io/spring-cloud-gateway/docs/4.0.4/reference/html/ 1.网关入门 helloword 网关不依赖start-web 导入的pom: <!--gateway--> <dependency><groupIdorg.springframework.cloud</groupId><arti…...

中望CAD 建筑 v2024 解锁版下载、安装教程 (超强的CAD三维制图)
前言 中望CAD建筑版是一款国产CAD制图软件,专注于建筑设计领域。中望CAD建筑版拥有丰富多样的建筑图块和图案,完美兼容各类建筑图纸。同时,它提供了绘图标准规范,使绘图更加规范和专业。更值得一提的是,该软件还具备智…...

windows edge自带的pdf分割工具(功能)
WPS分割pdf得会员,要充值!网上一顿乱找,发现最简单,最好用,免费的还是回到Windows。 Windows上直接在edge浏览器打开PDF,点击 打印 按钮,页面下选择对应页数 打印机 选择 另存为PDF,然后保存就…...

HTML5实现好看的天气预报网站源码
文章目录 1.设计来源1.1 获取天气接口1.2 PC端页面设计1.3 手机端页面设计 2.效果和源码2.1 动态效果2.2 源代码 源码下载万套模板,程序开发,在线开发,在线沟通 作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_4…...
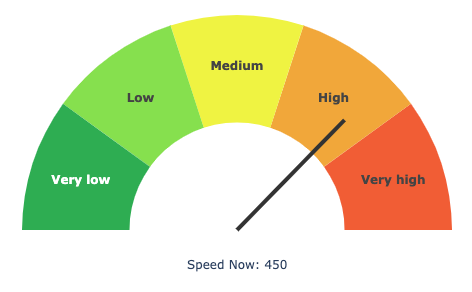
比较(八)利用python绘制指示器
比较(八)利用python绘制指示器 指示器(Indicators)简介 指示器是一系列相关图的统称,主要用于突出展示某一变量的实际值与目标值的差异,例如常见的数据delta、仪表盘、子弹图、水滴图等。 快速绘制 基于p…...

【体外诊断】ARM/X86+FPGA嵌入式计算机在医疗CT机中的应用
体外诊断 信迈科技提供基于Intel平台、AMD平台、NXP平台的核心板、2.5寸主板、Mini-ITX主板、4寸主板、PICO-ITX主板,以及嵌入式准系统等计算机硬件。产品支持GAHDMI等独立双显,提供丰富串口、USB、GPIO、PCIe扩展接口等I/O接口,扩展性强&…...

力扣 28找到字符串中第一个匹配项的下标 KMP算法
思路: 朴素匹配有很多步骤是多余的 KMP算法能够避免重复匹配 KMP算法主要是根据子串生成的next数组作为回退的依据,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。 这里讲一下为什么用模式串的最大公共前后缀…...
——匿名函数)
JavaScript(10)——匿名函数
匿名函数 没有名字的函数,无法直接使用。 使用方式: 函数表达式立即执行函数 函数表达式 将匿名函数赋值给一个变量,并且通过变量名称进行调用 let fn function(){ 函数体 } 调用: fn() 立即执行函数 语法: (function () {…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
