LeetCode 第407场周赛个人题解
目录
100372. 使两个整数相等的位更改次数
原题链接
思路分析
AC代码
100335. 字符串元音游戏
原题链接
思路分析
AC代码
100360. 将 1 移动到末尾的最大操作次数
原题链接
思路分析
AC代码
100329. 使数组等于目标数组所需的最少操作次数
原题链接
思路分析
AC代码
100372. 使两个整数相等的位更改次数
原题链接
100372. 使两个整数相等的位更改次数
思路分析
考虑不能存在某位k是1而n不是1,所以k必须是n的子集
n & k != k 就返回-1
否则返回 n ^ k 1 的 个数
时间复杂度:O(1)
AC代码
class Solution:def minChanges(self, n: int, k: int) -> int:if (n & k) != k:return -1return (n ^ k).bit_count()100335. 字符串元音游戏
原题链接
100335. 字符串元音游戏
思路分析
考虑如果有奇数个元音,那么Alice全拿完就赢了
如果有偶数个元音,记为cnt,那么Alice拿包含cnt - 1个元音的串,照样赢
于是得出:只要有元音就赢
时间复杂度:O(N)
AC代码
class Solution:def doesAliceWin(self, s: str) -> bool:st = set(['a', 'e', 'i', 'o', 'u'])return True if sum(1 for x in s if x in st) else False100360. 将 1 移动到末尾的最大操作次数
原题链接
100360. 将 1 移动到末尾的最大操作次数
思路分析
赛时写的分组循环,不好看,赛后改了下
我们考虑优先移动左边的1,如果优先移动右边的1那么所有左边的1都只能移动1次
那么我们直接遍历,每遇到一组连续0,前面1的贡献都+1
时间复杂度:O(N)
AC代码
class Solution:def maxOperations(self, s: str) -> int:res = c1 = 0n = len(s) for i, x in enumerate(s):if x == '1':c1 += 1elif i and s[i - 1] == '1':res += c1return res100329. 使数组等于目标数组所需的最少操作次数
原题链接
100329. 使数组等于目标数组所需的最少操作次数
思路分析
典中典的题,学差分的时候都会做这个类型的题目吧……
其实就是差分的一个结论:对于一个数组我们要将数组中每个数字变相等(每次可操作子数组-1/+1),最少操作次数为其差分数组从第二个数开始 的正数和 与 负数绝对值和 中大的那一个
为什么呢?
我们考虑原数组变相等 等价于 差分数组除了第一个数外全变为0,而区间操作对应差分数组中左边一个数+1 / -1,右边一个数执行相反操作
那么我们最优方案就是差分数组先正负抵消,再加上剩下的数字绝对值和
由于最后剩下的一定是正数或者负数,所以我们等价为 正数绝对值和 与 负数绝对值和 中 大的那一个
换到本题,等价于 nums - target 的数组全变0
等价于 nums - target 的差分数组全变0
和前面结论不同的是,结论是数组变相等,没有指定具体值,这里指定了0,所以就是整个差分数组的正数和 与 负数和的绝对值 中取大的那一个
时间复杂度:O(N)
AC代码
class Solution:def minimumOperations(self, nums: List[int], target: List[int]) -> int:n = len(nums)diff = [nums[i] - target[i] for i in range(n)]tmp = [nums[i] - target[i] for i in range(n)]for i in range(1, n):diff[i] = tmp[i] - tmp[i - 1]s1 = s2 = 0for x in diff:if x > 0:s1 += xelse:s2 -= xreturn max(s1, s2)相关文章:

LeetCode 第407场周赛个人题解
目录 100372. 使两个整数相等的位更改次数 原题链接 思路分析 AC代码 100335. 字符串元音游戏 原题链接 思路分析 AC代码 100360. 将 1 移动到末尾的最大操作次数 原题链接 思路分析 AC代码 100329. 使数组等于目标数组所需的最少操作次数 原题链接 思路分析 A…...

使用Django框架实现音频上传功能
数据库设计(models.py) class Music(models.Model):""" 音乐 """name models.CharField(verbose_name"音乐名字", max_length32)singer models.CharField(verbose_name"歌手", max_length32)# 本质…...

[路由器]IP-MAC的绑定与取消
背景:当公司的网络不想与外部人员进行共享,可以在路由器页面配置IP-MAC的绑定,让公司内部人员的手机和电脑的mac,才能接入到公司。第一步:在ARP防护中,启动IP-MAC绑定选项,必须启动仅允许IP-MAC…...
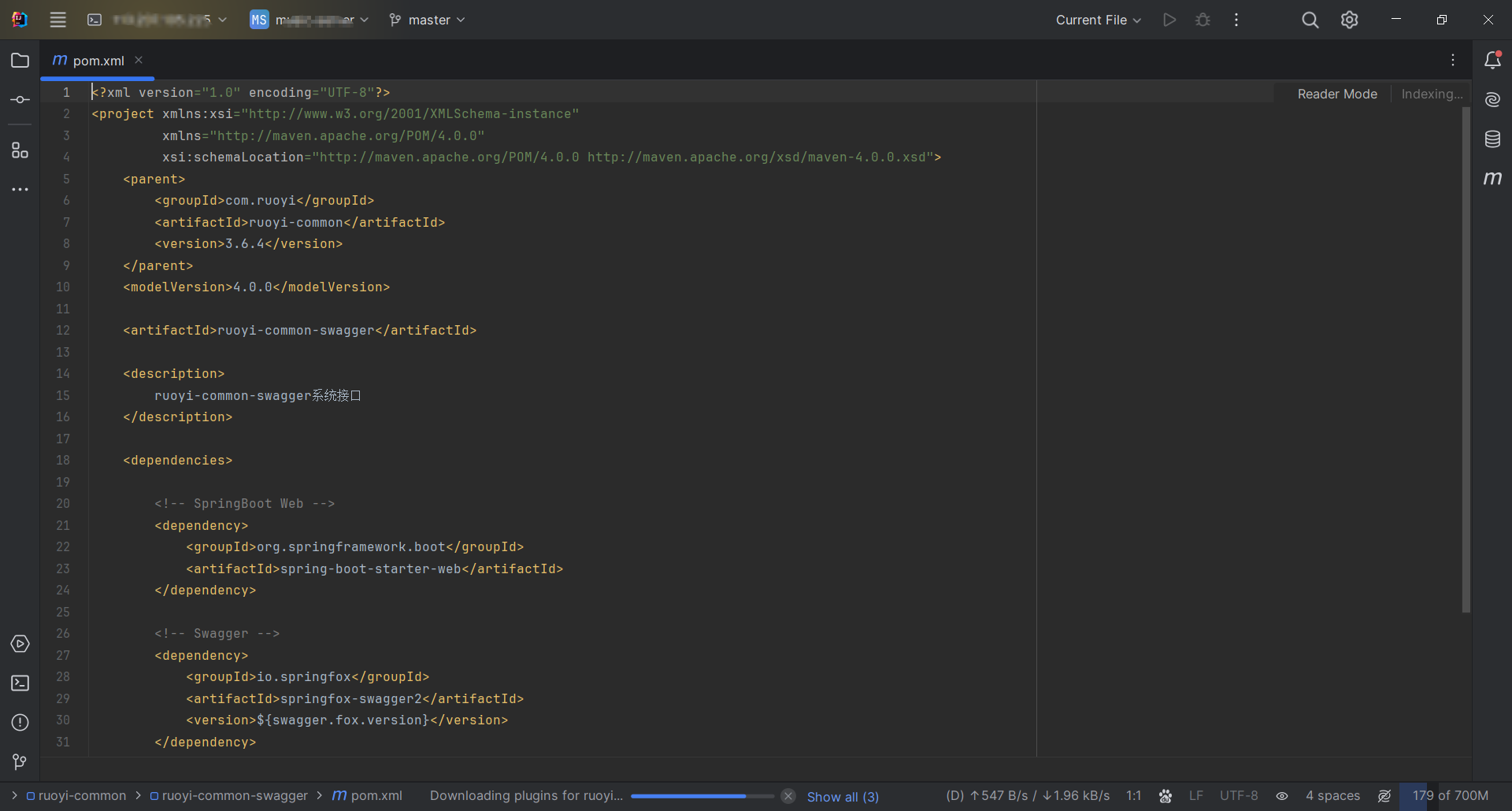
Idea配置远程开发
Idea配置远程开发 本篇博客介绍使用idea通过ssh连接ubuntu服务器进行开发 目录 Idea配置远程开发1.idae上点击file->Remote Development2.点击New Connection3.填写相关信息4.输入密码5.选择IDE版本和项目路径5.1 点击open an SSH terminal打开控制台5.2 依次执行命令 6.成…...

lua 实现 函数 判断两个时间戳是否在同一天
函数用于判断两个时间戳是否在同一天。下面是对代码的详细解释: ### 函数参数 - stampA 和 stampB:两个时间戳,用于比较。- resetInfo:一个可选参数,包含小时、分钟和秒数,用于调整时间戳。 ### 函数实现…...

工作纪实53-log4j日志打印文件隔离
在项目中,我有一堆业务日志需要打印,另一部分的日志,是没有格式的,需要被云平台离线解析并收集到kafka或者hdfs、hive等,需要将日志隔离打印到不同的文件 正常的log4j配置是下面这样的,配合Sl4j直接使用默认…...

7月21日,贪心练习
大家好呀,今天带来一些贪心算法的应用解题、 一,柠檬水找零 . - 力扣(LeetCode) 解析: 本题的贪心体现在对于20美元的处理上,我们总是优先把功能较少的10元作为找零,这样可以让5元用处更大 …...
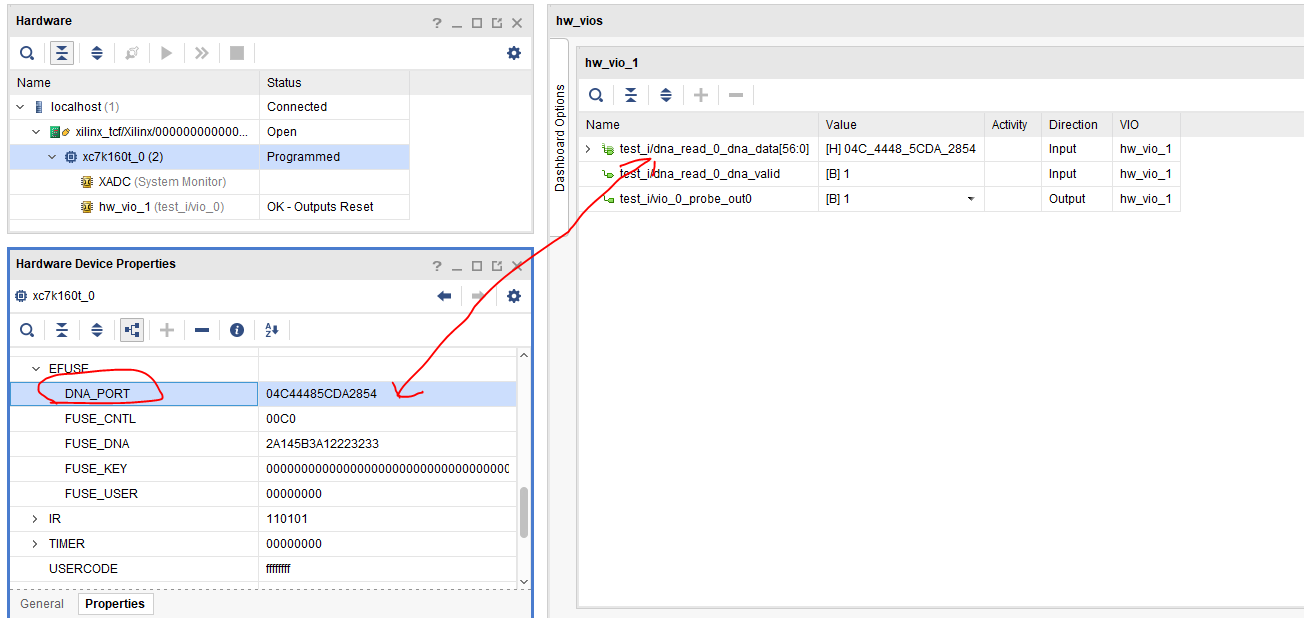
FPGA DNA 获取 DNA_PORT
FPGA DNA DNA 是 FPGA 芯片的唯一标识, FPGA 都有一个独特的 ID ,也就是 Device DNA ,这个 ID 相当于我们的身份证,在 FPGA 芯片生产的时候就已经固定在芯片的 eFuse 寄存器中,具有不可修改的属性。在 xilinx 7series…...

使用 hutool工具实现导入导出功能。
hutool工具网址 Hutool参考文档 pom依赖 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.7.20</version></dependency><dependency><groupId>org.apache.poi</gro…...

大语言模型-Transformer-Attention Is All You Need
一、背景信息: Transformer是一种由谷歌在2017年提出的深度学习模型。 主要用于自然语言处理(NLP)任务,特别是序列到序列(Sequence-to-Sequence)的学习问题,如机器翻译、文本生成等。Transfor…...
)
spring(二)
一、为对象类型属性赋值 方式一:(引用外部bean) 1.创建班级类Clazz package com.spring.beanpublic class Clazz {private Integer clazzId;private String clazzName;public Integer getClazzId() {return clazzId;}public void setClazzId(Integer clazzId) {th…...

MAC 数据恢复软件: STELLAR Data Recovery For MAC V. 12.1 更多增强功能
天津鸿萌科贸发展有限公司是 Stellar 系列软件的授权代理商。 STELLAR Data Recovery For MAC 该数据恢复软件可从任何存储驱动器、清空的回收站以及崩溃或无法启动的 Mac 设备中恢复丢失或删除的文件。 轻松恢复已删除的文档、照片、音频文件和视频。自定义扫描以帮助恢复特…...

初识godot游戏引擎并安装
简介 Godot是一款自由开源、由社区驱动的2D和3D游戏引擎。游戏开发虽复杂,却蕴含一定的通用规律,正是为了简化这些通用化的工作,游戏引擎应运而生。Godot引擎作为一款功能丰富的跨平台游戏引擎,通过统一的界面支持创建2D和3D游戏。…...

Windows配置Qt+VLC
文章目录 前言下载库文件提取文件编写qmakeqtvlc测试代码 总结 前言 在Windows平台上配置Qt和VLC是开发多媒体应用程序的一个重要步骤。Qt作为一个强大的跨平台应用开发框架,为开发人员提供了丰富的GUI工具和库,而VLC则是一个开源的多媒体播放器&#x…...

本地部署 mistralai/Mistral-Nemo-Instruct-2407
本地部署 mistralai/Mistral-Nemo-Instruct-2407 1. 创建虚拟环境2. 安装 fschat3. 安装 transformers4. 安装 flash-attn5. 安装 pytorch6. 启动 controller7. 启动 mistralai/Mistral-Nemo-Instruct-24078. 启动 api9. 访问 mistralai/Mistral-Nemo-Instruct-2407 1. 创建虚拟…...
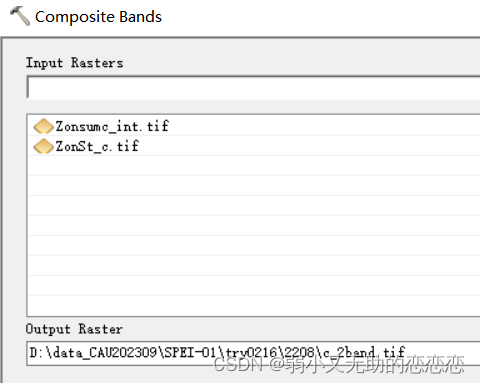
2月科研——arcgis计算植被差异
ArcGIS中,设置高于或低于某个值的像元为 -9999,然后将这些地方设为空——目的:去除异常值和黑色背景值 Con(("T_std ano7.tif" > 2) | ("T_std ano7.tif" < - 2), - 9999,"T_std ano7.tif") SetNull(&…...

深入理解Android中的缓存与文件存储目录
🌟 引言 在Android应用开发中,合理管理应用的数据存储至关重要。应用可能需要保存各种类型的数据,从简单的配置信息到多媒体文件,甚至是缓存数据以提高性能和用户体验。Android提供了多个内置目录来满足这些需求,但它…...

Linux_生产消费者模型
目录 1、生产消费者模型示意图 2、生产者消费者之间的关系 3、定义交易场所 4、实现生产消费者模型 5、伪唤醒 6、多生产多消费者的实际运用 7、POSIX信号量 7.1 初始化信号量 7.2 销毁信号量 7.3 等待信号量 7.4 发布信号量 8、生产消费的环形队列模型 8.1…...

【Vue】`v-if` 指令详解:条件渲染的高效实现
文章目录 一、v-if 指令概述二、v-if 的基本用法1. 基本用法2. 使用 v-else3. 使用 v-else-if 三、v-if 指令的高级用法1. 与 v-for 一起使用2. v-if 的性能优化 四、v-if 的常见应用场景1. 表单验证2. 弹窗控制 五、v-if 指令的注意事项 Vue.js 是一个用于构建用户界面的渐进式…...

junit mockito Base基类
编写单元测试时我们都习惯性减少重复代码 以下基于spring mvc框架,需要手动pom导包 BaseTest类用于启动上下文进行debug调试 MockBaseTset类用于不启动上下文进行打桩mock pom.xml <dependency><groupId>org.mockito</groupId><artifactId…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...
