【手撕八大排序】——插入排序
文章目录
- 插入排序概念
- 插入排序分为2种
- 一 .直接插入排序
- 直接插入排序时间复杂度
- 二.希尔排序
- 希尔排序时间复杂度
- 效率比较
插入排序概念
直接插入排序是从一个有序的序列中选择一个合适的位置进行插入,这个合适的位置取决于是要升序排序还是降序排序。
每一次进行排序之后,这段数据都是有序的。
提示:以下是本篇文章正文内容,下面案例可供参考
插入排序分为2种
一 .直接插入排序
直接插入排序是从一段数据中将一个数据在合适的位置插入。
案例:
一张图弄懂直接插入排序
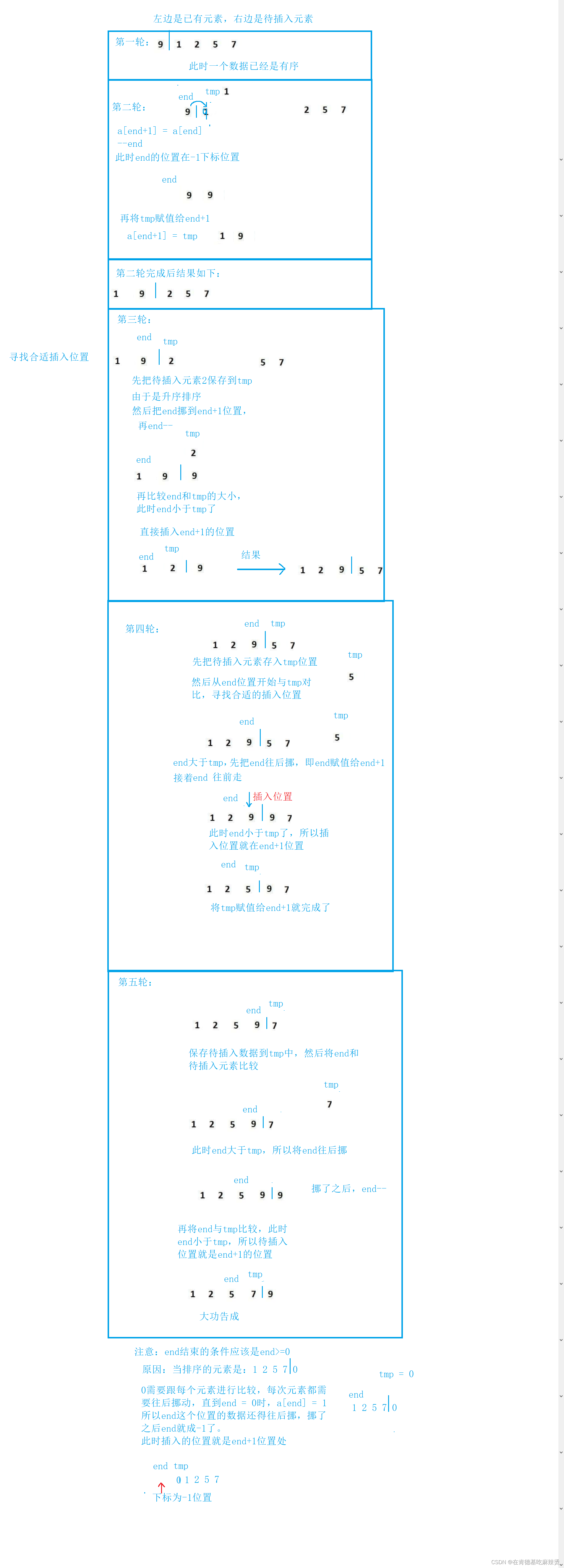

代码如下:
void InsertSort(int * a,int n )
{for(int i =0;i<n-1;i++){int end = i;//保存待插入元素int tmp = a[end+1];while(end>=0){if(a[end]>tmp){//把end往后挪a[end+1] = a[end];//end再往前走 end--;}else{break;}}//由于不管是在中间的任意地方插入还是在end的末尾插入(即tmp是最大的情况),//都是在end后面的位置插入,所以来到这里进行合并a[end+1] = tmp;}
}直接插入排序时间复杂度
直接插入排序的时间复杂度为:O(N^2),因为最坏的情况是逆序的情况:

每一次插入需要挪动的次数为:1+2+3+4+…+n-2+n-1 = n*n/2
所以最坏情况下的时间复杂度为O(n^2)
二.希尔排序
希尔排序可以被认为是优化后的直接插入排序。
具体优化过程如下:
给定一个gap,这个gap是把待插入的数据分成gap组,每组之间的间隔为gap长度
给定一个gap,这个gap是把待插入的数据分成gap组,每组之间的间隔为gap长度
给定一个gap,这个gap是把待插入的数据分成gap组,每组之间的间隔为gap长度
重要的事情说三遍。
比如:
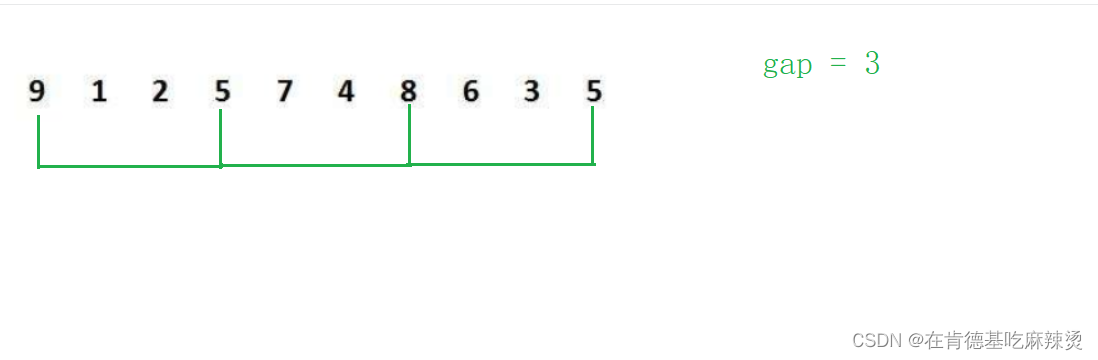
令gap = 3,即待插入的数据的间隔为3,不同于直接插入排序,直接插入排序是第一个和第二个数据的间隔永远为1,而对于希尔排序,当gap = 3时,第一个数据和第二个数据的间隔为3。
当我们把该组的元素两两比较时,大的元素就会更快地往后走。
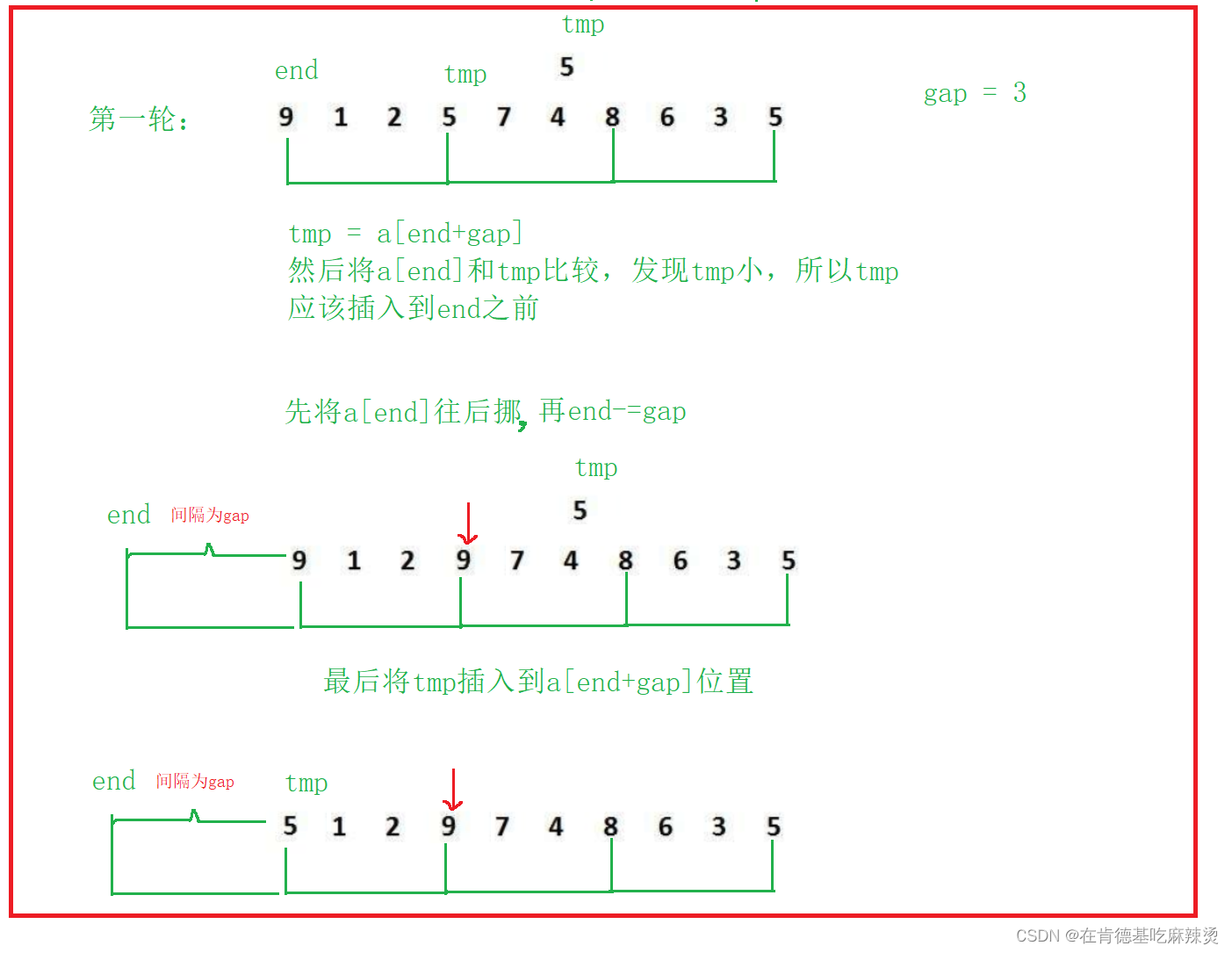
第二轮是将待插入元素8和9比较,因为9后面的第一个元素不再是7,而是9+gap的位置处的数据,即8
再将9和8进行比较,将8插入到9位置处。
当然,这是每组组内的比较,
放眼整个希尔排序来说,是多组同时进行的。
可以发现,
当gap越大,大的元素越快挪到后面
当gap越小,小的元素越慢挪到后面
当gap == 1时,就相当于上面提到的直接插入排序。
回到上面的案例,gap = 3,所以需要将数据分成3组,每组的间隔为3个长度。

如上图:此时每个元素都可以被覆盖到。
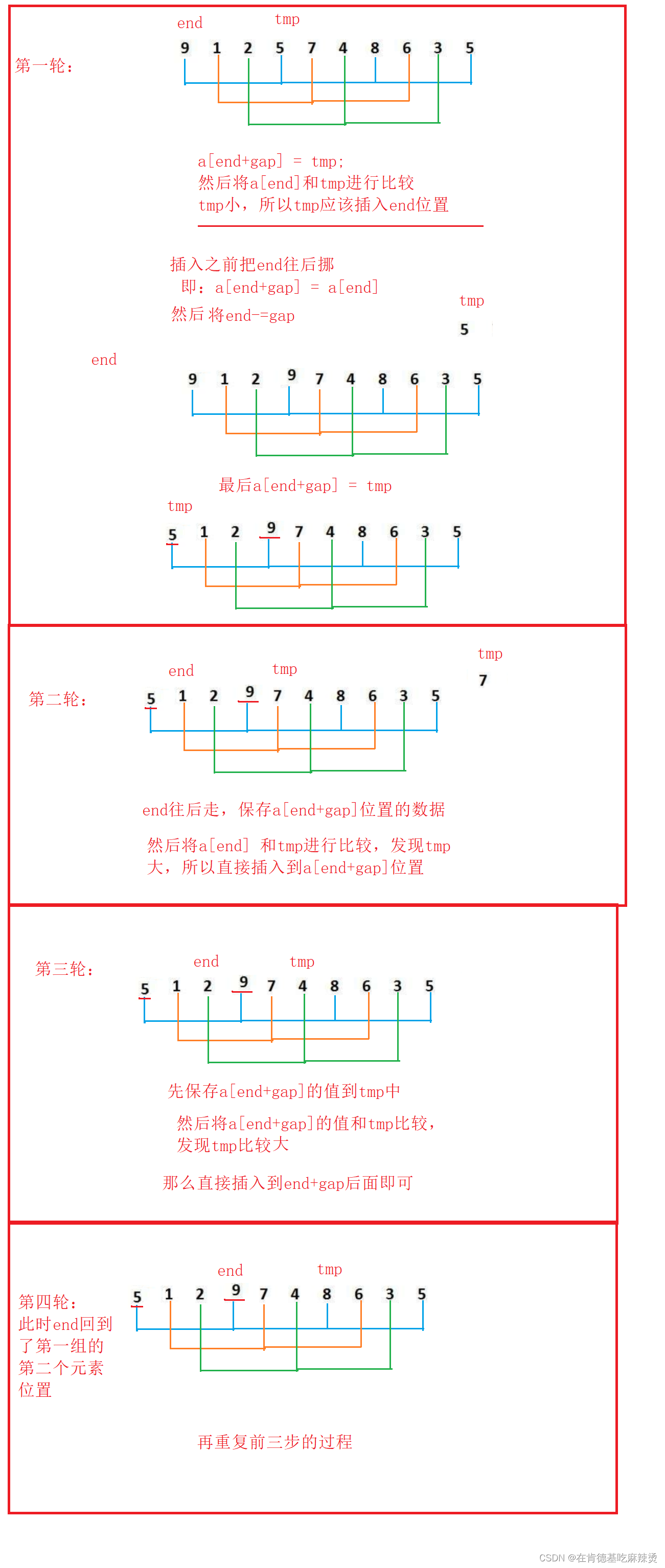
相当于同时把gap组中大的元素更快挪到后面
我们把上面的过程成为:预排序
也就是说,完成上面的操作之后,整个数据并不是有序的,而是 接近有序
比如上面的案例,完成预排序后,整组数据为:

此时是接近有序,所以此时令gap = 1,即最后接近有序的时候进行直接插入排序即可。
注意:gap的取值是不确定的:
gap取值越大,大的数据越快挪到后面,但越不接近有序
gap取值越小,大的数据越慢挪到后面,但越接近有序
总之gap是一定不能固定,并且gap的取值最后必须为1。
gap的取值应该是从大逐渐到小过渡的。
gap的取值一般是:
初始化gap = n,
进入轮回时:
gap = gap/3+1 或者 gap = gap/2,每次轮完一轮后,gap都会减小。
当gap的取值是gap = gap/2时,时间复杂度为:O(N*logN),logN是以2为底N的对数
最坏情况同样为逆序:
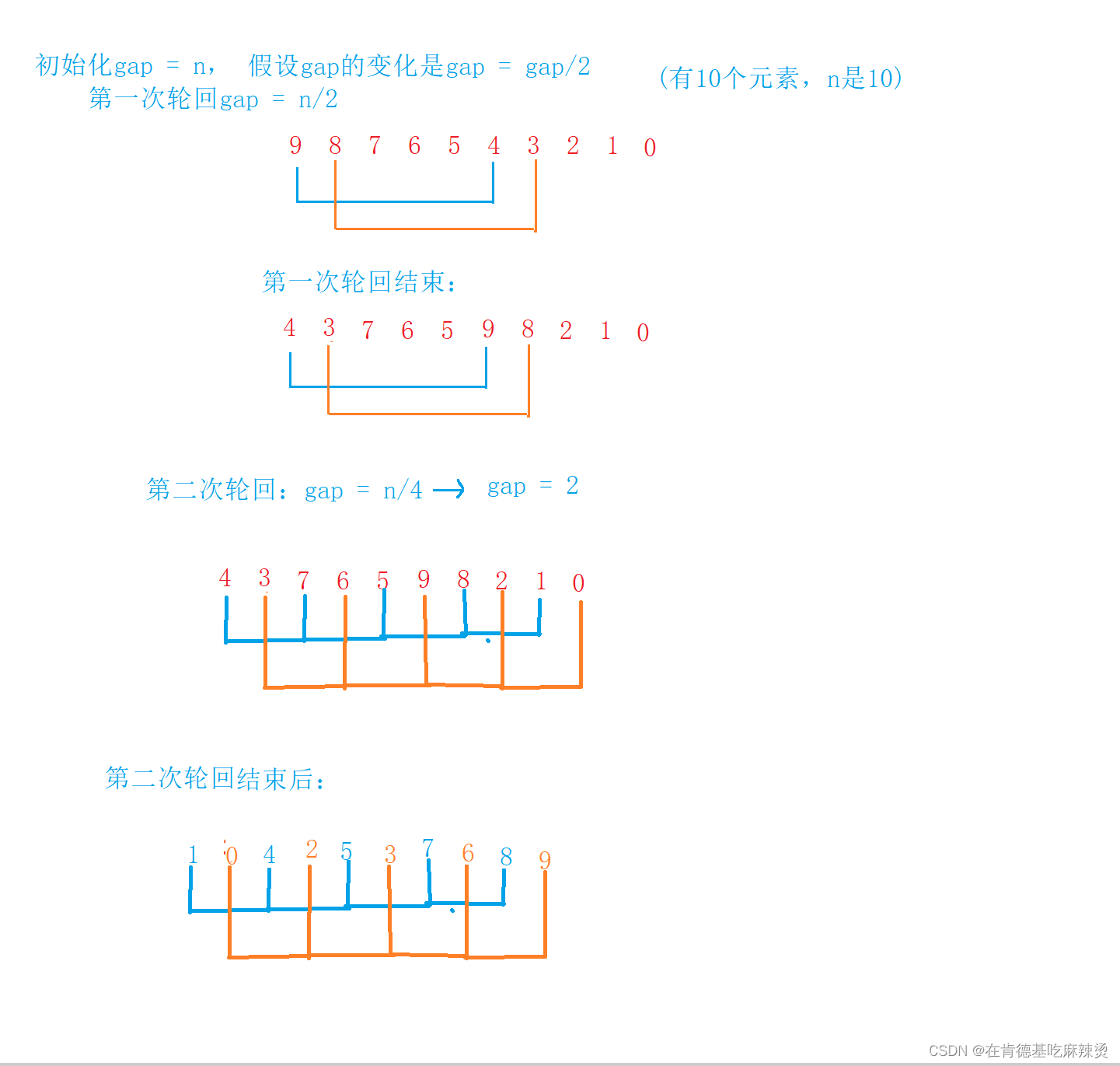
最后一轮gap = 1,此时为直接插入排序,则N/2/2/2/…/2 = 1,
每次轮回一次gap,gap都会/2,最后一次gap = 1,则需要比较的次数是logN(以2为底N的对数)
希尔排序时间复杂度
总的时间复杂度为遍历整组元素的次数:O(N)*每次遍历进行插入的次数O(logN)
—> O(N * logN)
同理:当gap的变化是gap = gap/3-1时, 最坏情况下(逆序)每次轮回需要插入的次数是
(((N/3+1) /3+1)/3+1)… = 1
对于时间复杂度:可忽略掉+1项,所以每次轮回插入次数log3 (N) ,以3为底N的对数
总时间复杂度为O(N*log3 (N))
经过前人计算,希尔排序平均时间复杂度为:
O(N^1.3)

实现代码:
void ShellSort(int* a, int n)
{//当gap越大,大的值越快到达最后的位置,但越不接近有序//当gap越小,大的值越慢到达最后的位置,但越接近有序//当gap值越接近1,排序越接近顺序//刚gap == 1时,就是直接插入排序int gap = n;while (gap > 1){//两种方式均可,gap可以任取任何值,但是都必须保证gap最后一定为1//gap = gap / 2;gap = gap / 3 + 1;//在这里就是把间隔多组的数据同时排列for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){//小于的情况,需要挪动数据if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}//大于或者等于的情况,直接插入end后面else{break;}}//由于最终都需要插入end后面,所以在循环之外插入a[end + gap] = tmp;}}
}总结:希尔排序是在直接插入排序的基础上引入一个gap,这个gap把数据分成了gap组,并且每组元素之间的间隔也为gap。
gap每次都会逐渐减小,并且最后gap一定为1,当gap为1时,代表完成了预排序,
最后一步进行直接插入排序。
效率比较
void TestOP()
{srand(time(0));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);assert(a1 && a2);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];}//计算到这个走位置的时间(ms)int begin1 = clock();InsertSort(a1, N);int end1 = clock();//末位置-初位置就是时间差int begin2 = clock();ShellSort(a2, N);int end2 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);free(a1);free(a2);
}int main()
{TestOP();return 0;
}
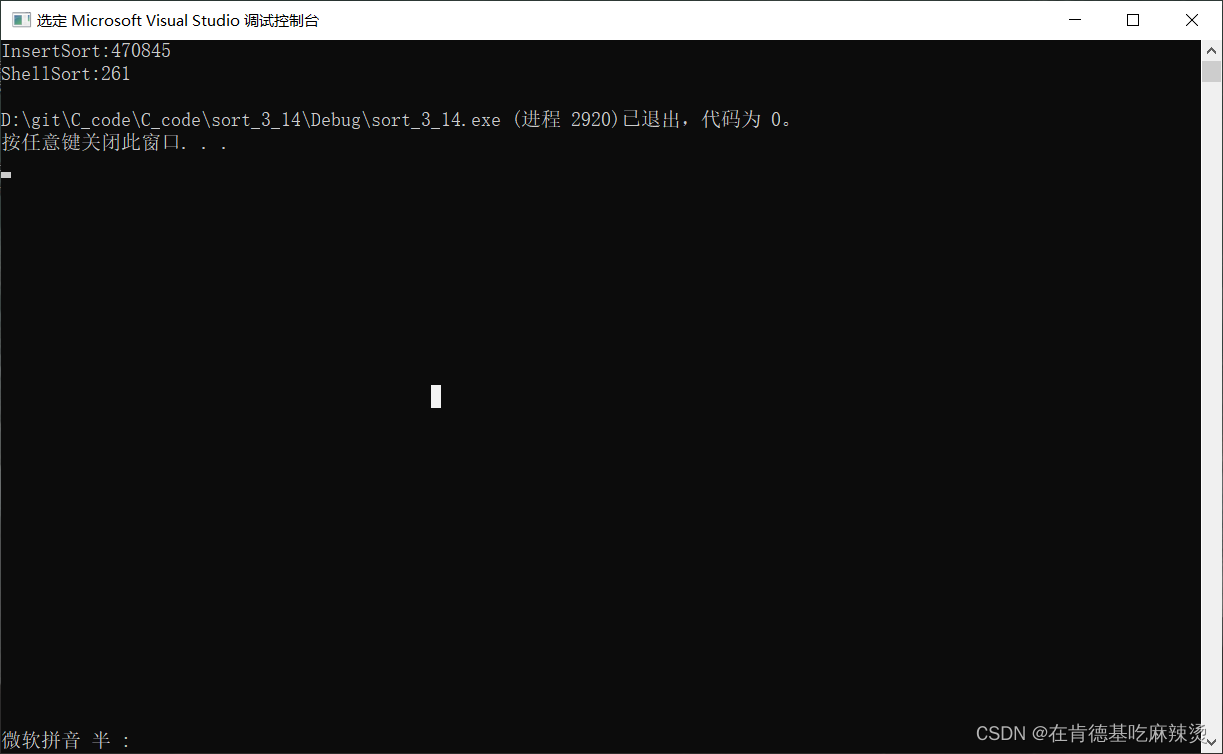
可以看到,当排序数据为100w个时,直接插入排序和希尔排序差距超过了2000倍。
直接插入排序和希尔排序的效率相比,数据越多,希尔排序较于直接插入排序的优化越大。
相关文章:

【手撕八大排序】——插入排序
文章目录插入排序概念插入排序分为2种一 .直接插入排序直接插入排序时间复杂度二.希尔排序希尔排序时间复杂度效率比较插入排序概念 直接插入排序是从一个有序的序列中选择一个合适的位置进行插入,这个合适的位置取决于是要升序排序还是降序排序。 每一次进行排序…...
flink多流操作(connect cogroup union broadcast)
flink多流操作1 分流操作2 connect连接操作2.1 connect 连接(DataStream,DataStream→ConnectedStreams)2.2 coMap(ConnectedStreams → DataStream)2.3 coFlatMap(ConnectedStreams → DataStream)3 union操作3.1 uni…...

漫画:什么是快速排序算法?
这篇文章,以对话的方式,详细着讲解了快速排序以及排序排序的一些优化。 一禅:归并排序是一种基于分治思想的排序,处理的时候可以采取递归的方式来处理子问题。我弄个例子吧,好理解点。例如对于这个数组arr[] { 4&…...

vue 3.0组件(下)
文章目录前言:一,透传属性和事件1. 如何“透传属性和事件”2.如何禁止“透传属性和事件”3.多根元素的“透传属性和事件”4. 访问“透传属性和事件”二,插槽1. 什么是插槽2. 具名插槽3. 作用域插槽三,单文件组件CSS功能1. 组件作用…...
双指针 -876. 链表的中间结点-leetcode
开始一个专栏,写自己的博客 双指针,也算是作为自己的笔记吧! 双指针从广义上来说,是指用两个变量在线性结构上遍历而解决的问题。狭义上说, 对于数组,指两个变量在数组上相向移动解决的问题;对…...

Linux之运行级别
文章目录一、指定运行级别基本介绍CentOS7后运行级别说明一、指定运行级别 基本介绍 运行级别说明: 0:关机 1:单用户【找回丢失密码】 2:多用户状态没有网络服务 3:多用户状态有网络服务 4:系统未使用保留给用户 5:图形界面 6:系统重启 常用运行级别是3和5,也可以…...

python搭建web服务器
前言:相信看到这篇文章的小伙伴都或多或少有一些编程基础,懂得一些linux的基本命令了吧,本篇文章将带领大家服务器如何部署一个使用django框架开发的一个网站进行云服务器端的部署。 文章使用到的的工具 Python:一种编程语言&…...
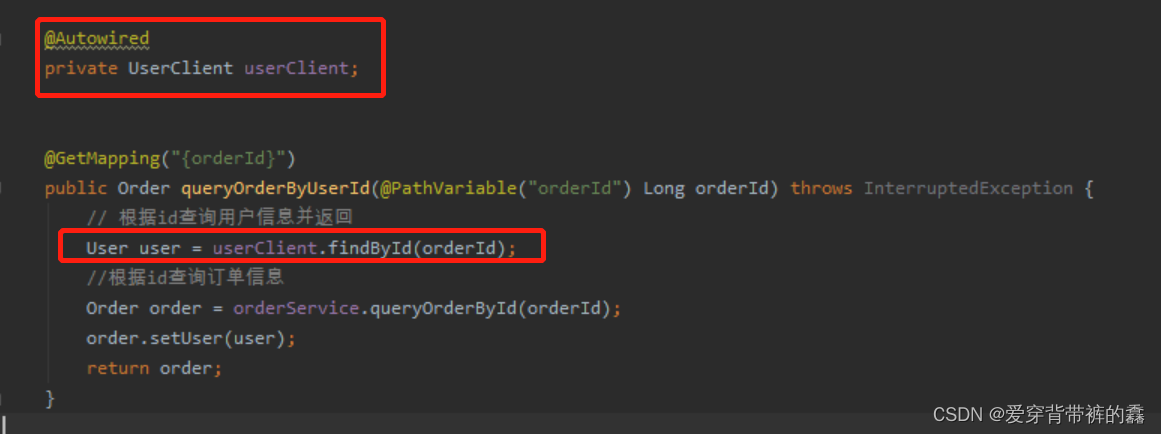
【SpringCloud】SpringCloud Feign详解
目录前言SpringCloud Feign远程服务调用一.远程调用逻辑图二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用四.构建Feign五.自定义Feign配置六.Feign配置日志七.Feign调优八.抽离Feign前言 微服务分解成多个不同的服务,那么多个服务之间怎么调用呢&…...

更改Hive元数据发生的生产事故
今天同事想在hive里用中文做为分区字段。如果用中文做分区字段的话,就需要更改Hive元 数据库。结果发生了生产事故。导致无法删除表和删除分区。记一下。 修改hive元数据库的编码方式为utf后可以支持中文,执行以下语句: alter table PARTITI…...
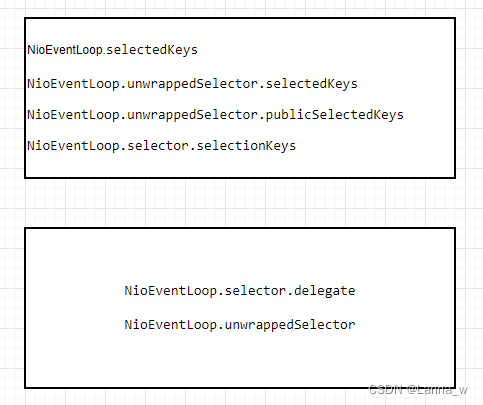
《Netty》从零开始学netty源码(八)之NioEventLoop.selector
目录java原生的WEPollSelectorImplnetty的SelectionKey容器SelectedSelectionKeySetnetty的SelectedSelectionKeySetSelectorSelectorTupleopenSelector每一个NioEventLoop配一个选择器Selector,在创建NioEventLoop的构造函数中会调用其自身方法openSelector获取sel…...
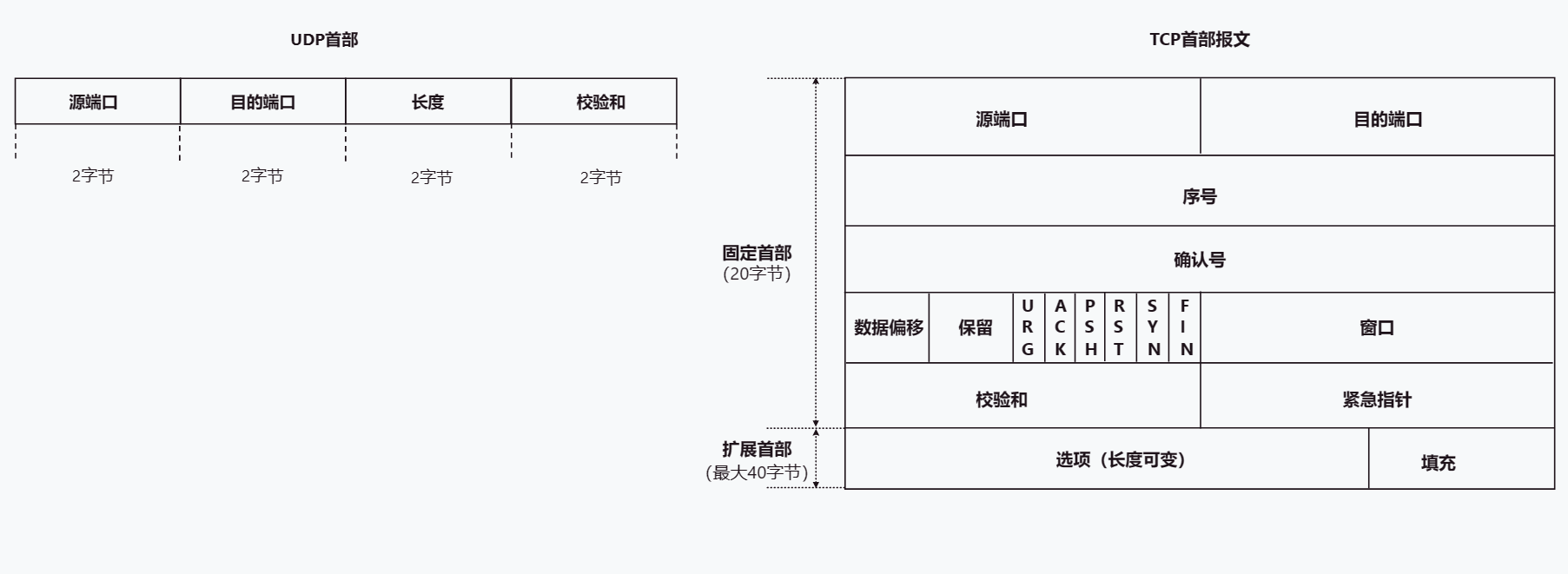
TCP UDP详解
文章目录TCP UDP协议1. 概述2. 端口号 复用 分用3. TCP3.1 TCP首部格式3.2 建立连接-三次握手3.3 释放连接-四次挥手3.4 TCP流量控制3.5 TCP拥塞控制3.6 TCP可靠传输的实现3.7 TCP超时重传4. UDP5.TCP与UDP的区别TCP UDP协议 1. 概述 TCP、UDP协议是TCP/IP体系结构传输层中的…...
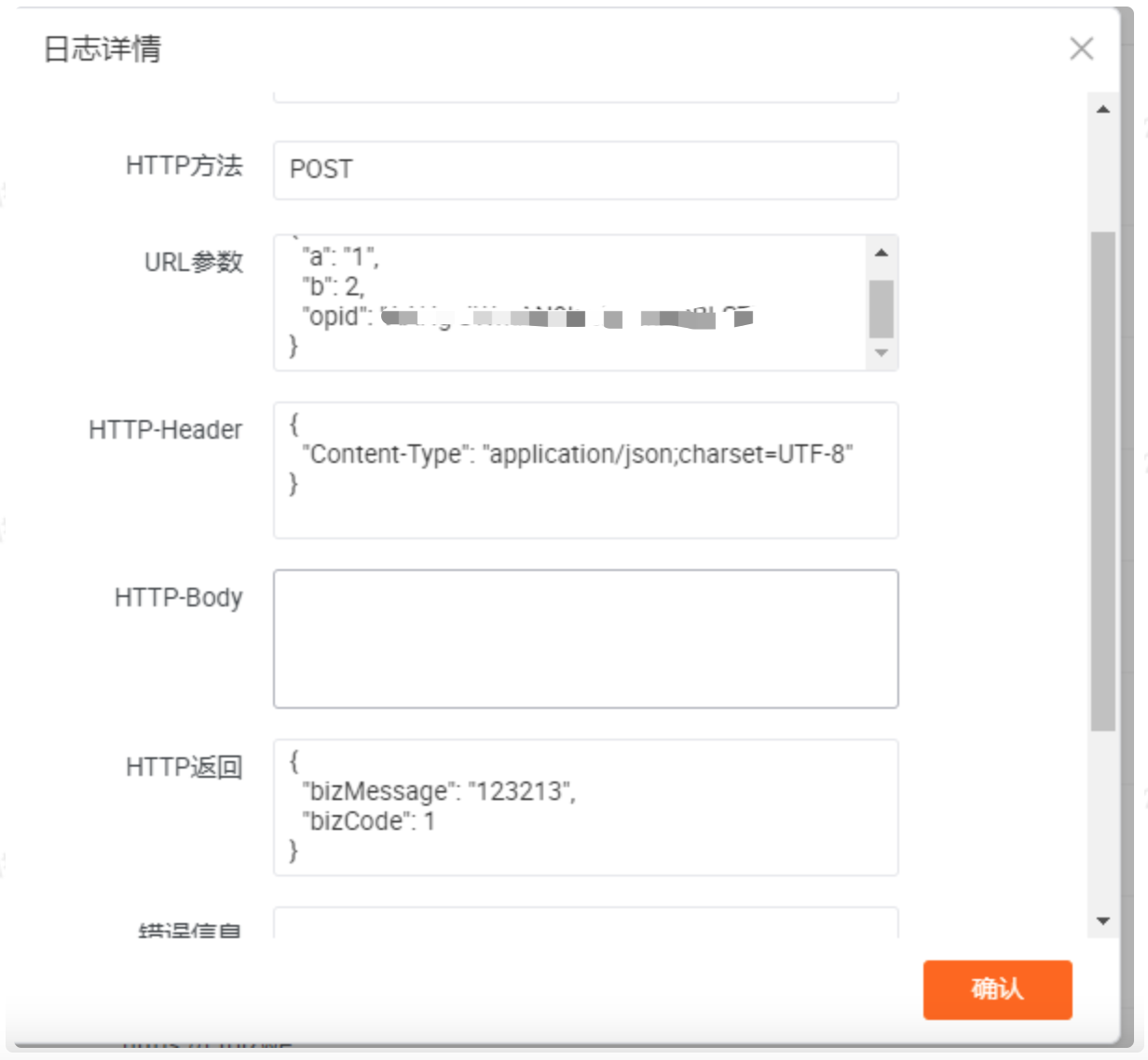
超详细淘宝小程序的接入开发步骤
本文是向大家介绍的关于工作中遇到的如何对接淘宝小程序开发的步骤,它能够帮助大家省略在和淘宝侧对接沟通过程中的一些繁琐问题,便捷大家直接快速开展工作~~一、步骤演示1、首先我们打开淘宝开放平台,进入控制台2、进入控制台后,…...
【Python】正则表达式re库
文章目录函数re.match函数re.search函数re.findall函数re.compile函数re.sub函数re.split函数修饰符正则表达式模式正则表达式实例函数 re.match函数 re.match()函数用于尝试从字符串的 起始位置 匹配一个模式,匹配成功返回一个匹配对象,否则返回None。…...

JDK8使用Visual VM根据Dump文件排查OutOfMemoryError生产问题思路
文章目录1. 前言2. 堆内存溢出3. GC执行异常4. 元空间内存溢出5. 创建线程异常6. 内存交换问题7. 数组长度过大8. 系统误杀异常1. 前言 当系统异常产生了dump文件需要我们对其进行排查时,其本质上考验的是我们对于Java运行时内存结构的知识掌握是否牢固以及对业务代…...
2023年网络安全比赛--网络安全事件响应中职组(超详细)
一、竞赛时间 180分钟 共计3小时 二、竞赛阶段 1.找出黑客植入到系统中的二进制木马程序,并将木马程序的名称作为Flag值(若存在多个提交时使用英文逗号隔开,例如bin,sbin,…)提交; 2.找出被黑客修改的系统默认指令,并将被修改的指令里最后一个单词作为Flag值提交; 3.找出…...

【半监督学习】3、PseCo | FPN 错位对齐的高效半监督目标检测器
文章目录一、背景二、方法2.1 基础框架结构2.2 带噪声的伪边界框学习2.3 多视图尺度不变性学习三、实验论文:PseCo: Pseudo Labeling and Consistency Training for Semi-Supervised Object Detection 代码:https://github.com/ligang-cs/PseCo 出处&a…...
Tomcat+Servlet初识
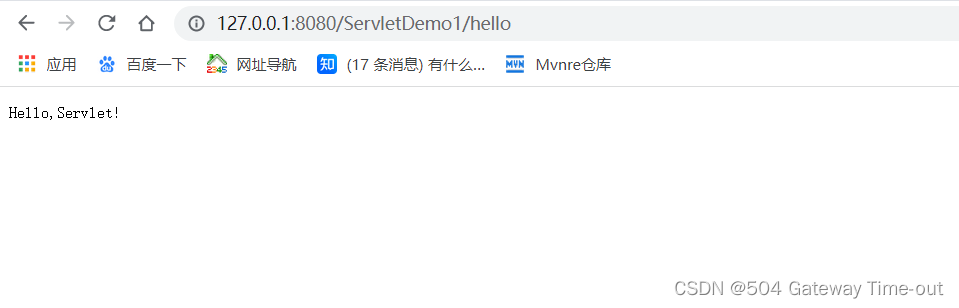
文章目录Tomcat什么是TomcatTomcat的安装启动tomcat静态页面的访问动态页面的访问一个Servlet程序的部署流程Tomcat 什么是Tomcat Tomcat是一个HTTP服务器,在开发或调试Servlet代码时应用广泛;使用Tomcat,实际就是将用户浏览器输入的http请…...
ChatGPT-4 终于来了(文末附免费体验地址)
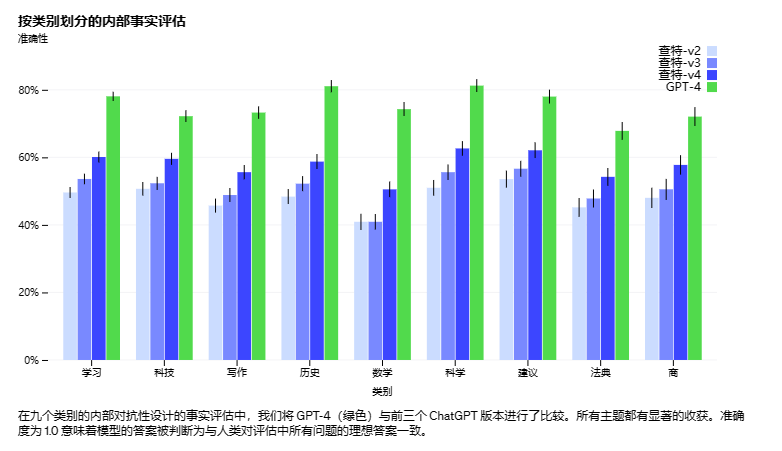
大家好,我是小钱学长。 ChatGPT4.0 重磅来袭,今天一打开plus页面出现的就是这个GPT-4的体验界面!现在就带大家一起看看GPT4.0。 进入之后是这样的 看到最下面有一行话,目前应该是4个小时限制100条消息。 GPT-4有什么优势&…...

【C++学习】类和对象(中)一招带你彻底了解六大默认成员函数
前言:在之前,我们对类和对象的上篇进行了讲解,今天我们我将给大家带来的是类和对象中篇的学习,继续深入探讨【C】中类和对象的相关知识!!! 目录 1. 类的6个默认成员函数 2. 构造函数 2.1概念介…...

面试——Java基础
说一说你对Java访问权限的了解 在修饰成员变量/成员方法时,该成员的四种访问权限的含义如下: private:该成员可以被该类内部成员访问; default:该成员可以被该类内部成员访问,也可以被同一包下其他的类访…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
