奇异值分解(SVD)原理与在降维中的应用
奇异值分解(SVD)原理与在降维中的应用
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结,并讨论在在PCA降维算法中是如何运用运用SVD的。
1. 回顾特征值和特征向量
我们首先回顾下特征值和特征向量的定义如下:Ax=λxAx=\lambda xAx=λx
其中A是一个n×nn \times nn×n的矩阵,x是一个n维向量,则我们说λ\lambdaλ是矩阵A的一个特征值,而x是矩阵A的特征值λ\lambdaλ所对应的特征向量。
求出特征值和特征向量有什么好处呢? 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值λ1≤λ2≤...≤λn\lambda_1 \leq \lambda_2 \leq ... \leq \lambda_nλ1≤λ2≤...≤λn,以及这n个特征值所对应的特征向量{w1,w2,...wn}\{w_1,w_2,...w_n\}{w1,w2,...wn},那么矩阵A就可以用下式的特征分解表示:A=WΣW−1A=W\Sigma W^{-1}A=WΣW−1
其中W是这n个特征向量所张成的n×nn \times nn×n维矩阵,而Σ\SigmaΣ为这n个特征值为主对角线的n×nn \times nn×n维矩阵。
一般我们会把W的这n个特征向量标准化,即满足∣∣wi∣∣2=1||w_i||_2 =1∣∣wi∣∣2=1, 或者说wiTwi=1w_i^Tw_i =1wiTwi=1,此时W的n个特征向量为标准正交基,满足WTW=IW^TW=IWTW=I,即WT=W−1W^T=W^{-1}WT=W−1, 也就是说W为酉矩阵。
这样我们的特征分解表达式可以写成A=WΣWTA=W\Sigma W^TA=WΣWT
注意到要进行特征分解,矩阵A必须为方阵。那么如果A不是方阵,即行和列不相同时,我们还可以对矩阵进行分解吗?答案是可以,此时我们的SVD登场了。
2. SVD的定义
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×nm \times nm×n的矩阵,那么我们定义矩阵A的SVD为:A=UΣVTA = U\Sigma V^TA=UΣVT
其中U是一个m×mm \times mm×m的矩阵,Σ\SigmaΣ是一个m×nm \times nm×n的矩阵,除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值,V是一个n×nn \times nn×n的矩阵。U和V都是酉矩阵,即满足UTU=I,VTV=IU^TU=I, V^TV=IUTU=I,VTV=I。下图可以很形象的看出上面SVD的定义:
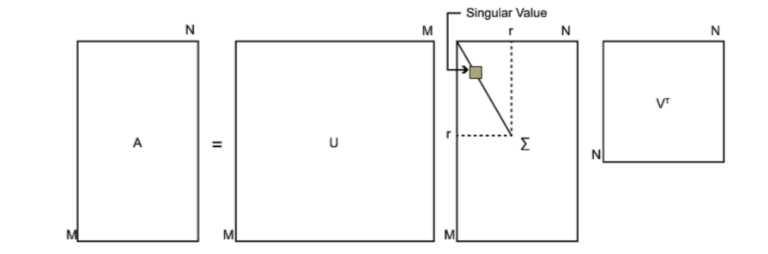
那么我们如何求出SVD分解后的U, Σ\SigmaΣ, V这三个矩阵呢?
如果我们将A的转置和A做矩阵乘法,那么会得到n×nn \times nn×n的一个方阵ATAA^TAATA。既然ATAA^TAATA是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:(ATA)vi=λivi(A^TA)v_i = \lambda_i v_i(ATA)vi=λivi
这样我们就可以得到矩阵ATAA^TAATA的n个特征值和对应的n个特征向量v了。将ATAA^TAATA的所有特征向量张成一个n×nn \times nn×n的矩阵V,就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
如果我们将A和A的转置做矩阵乘法,那么会得到m×mm \times mm×m的一个方阵AATAA^TAAT。既然AATAA^TAAT是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:(AAT)ui=λiui(AA^T)u_i = \lambda_i u_i(AAT)ui=λiui
这样我们就可以得到矩阵AATAA^TAAT的m个特征值和对应的m个特征向量u了。将AATAA^TAAT的所有特征向量张成一个m×mm \times mm×m的矩阵U,就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。
U和V我们都求出来了,现在就剩下奇异值矩阵Σ\SigmaΣ没有求出了。由于Σ\SigmaΣ除了对角线上是奇异值其他位置都是0,那我们只需要求出每个奇异值σ\sigmaσ就可以了。
我们注意到:A=UΣVT⇒AV=UΣVTV⇒AV=UΣ⇒Avi=σiui⇒σi=AviuiA=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i = \sigma_i u_i \Rightarrow \sigma_i = \frac {Av_i} {u_i}A=UΣVT⇒AV=UΣVTV⇒AV=UΣ⇒Avi=σiui⇒σi=uiAvi
这样我们可以求出我们的每个奇异值,进而求出奇异值矩阵Σ\SigmaΣ。
上面还有一个问题没有讲,就是我们说ATAA^TAATA的特征向量组成的就是我们SVD中的V矩阵,而AATAA^TAAT的特征向量组成的就是我们SVD中的U矩阵,这有什么根据吗?这个其实很容易证明,我们以V矩阵的证明为例。A=UΣVT⇒AT=VΣUT⇒ATA=VΣUTUΣVT=VΣ2VTA=U\Sigma V^T \Rightarrow A^T=V\Sigma U^T \Rightarrow A^TA =V\Sigma U^TU\Sigma V^T = V\Sigma^2V^TA=UΣVT⇒AT=VΣUT⇒ATA=VΣUTUΣVT=VΣ2VT
上式证明使用了:UTU=I,ΣT=ΣU^TU=I, \Sigma^T=\SigmaUTU=I,ΣT=Σ。可以看出ATAA^TAATA的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到AATAA^TAAT的特征向量组成的就是我们SVD中的U矩阵。
进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:σi=λi\sigma_i = \sqrt{\lambda_i}σi=λi
这样也就是说,我们可以不用σi=Aviui\sigma_i =\frac {Av_i}{u_i}σi=uiAvi来计算奇异值,也可以通过求出ATAA^TAATA的特征值取平方根来求奇异值。
3. SVD计算举例
这里我们用一个简单的例子来说明矩阵是如何进行奇异值分解的。我们的矩阵A定义为:
A=(011110)\mathbf{A} = \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1&0 \end{array} \right)A=011110
我们首先求出ATAA^TAATA和AATAA^TAAT
ATA=(011110)(011110)=(2112)\mathbf{A^TA} = \left( \begin{array}{ccc} 0& 1 &1\\ 1&1&0 \end{array} \right) \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1&0 \end{array} \right) = \left( \begin{array}{ccc} 2& 1 \\ 1&2 \end{array} \right)ATA=(011110)011110=(2112)
AAT=(011110)(011110)=(110121011)\mathbf{AA^T} = \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1&0 \end{array} \right) \left( \begin{array}{ccc} 0& 1 &1\\ 1&1&0 \end{array} \right) = \left(\begin{array}{ccc} 1& 1 &0\\1& 2 &1\\ 0& 1&1 \end{array} \right)AAT=011110(011110)=110121011
进而求出ATAA^TAATA的特征值和特征向量:λ1=3;v1=(1212);λ2=1;v2=(−1212)\lambda_1= 3; v_1 = \left( \begin{array}{ccc} \frac {1} {\sqrt{2}} \\ \frac {1} {\sqrt{2}}\end{array} \right); \lambda_2= 1; v_2 = \left( \begin{array}{ccc} \frac {-1}{\sqrt{2}} \\ \frac {1} {\sqrt{2}}\end{array} \right)λ1=3;v1=(2121);λ2=1;v2=(2−121)
接着求AATAA^TAAT的特征值和特征向量:
λ1=3;u1=(162616);λ2=1;u2=(120−12);λ3=0;u3=(13−1313)\lambda_1= 3; u_1 = \left( \begin{array}{ccc} \frac {1} {\sqrt{6}}\\ \frac {2} {\sqrt{6}} \\ \frac {1} {\sqrt{6}}\end{array} \right); \lambda_2= 1; u_2 = \left( \begin{array}{ccc} \frac {1} {\sqrt{2}} \\ 0 \\ \frac {-1} {\sqrt{2}}\end{array} \right); \lambda_3= 0; u_3 = \left( \begin{array}{ccc} \frac {1} {\sqrt{3}} \\ \frac {-1} {\sqrt{3}}\\ \frac {1} {\sqrt{3}}\end{array} \right)λ1=3;u1=616261;λ2=1;u2=2102−1;λ3=0;u3=313−131
利用Avi=σiui,i=1,2Av_i = \sigma_i u_i, i=1,2Avi=σiui,i=1,2求奇异值:
(011110)(1212)=σ1(162616)⇒σ1=3\left(\begin{array}{ccc} 0& 1\\1& 1\\ 1&0 \end{array} \right) \left( \begin{array}{ccc} \frac {1} {\sqrt{2}} \\ \frac {1} {\sqrt{2}}\end{array} \right) = \sigma_1 \left( \begin{array}{ccc} \frac {1} {\sqrt{6}} \\\frac {2} {\sqrt{6}} \\ \frac {1} {\sqrt{6}}\end{array} \right)\Rightarrow \sigma_1=\sqrt{3}011110(2121)=σ1616261⇒σ1=3
(011110)(−1212)=σ2(120−12)⇒σ2=1\left( \begin{array}{ccc} 0& 1\\1& 1\\1&0 \end{array} \right) \left( \begin{array}{ccc} \frac {-1} {\sqrt{2}}\\ \frac {1} {\sqrt{2}} \end{array} \right) = \sigma_2 \left( \begin{array}{ccc} \frac {1} {\sqrt{2}} \\ 0 \\ \frac {-1} {\sqrt{2}}\end{array} \right)\Rightarrow \sigma_2=1011110(2−121)=σ22102−1⇒σ2=1
当然,我们也可以用σi=λi\sigma_i = \sqrt{\lambda_i}σi=λi直接求出奇异值为3\sqrt{3}3和1.
最终得到A的奇异值分解为:A=UΣVT=(161213260−1316−1213)(300100)(1212−1212)A=U\Sigma V^T = \left( \begin{array}{ccc} \frac {1} {\sqrt{6}} & \frac {1} {\sqrt{2}} & \frac {1} {\sqrt{3}}\\\frac {2} {\sqrt{6}} & 0 & \frac {-1} {\sqrt{3}}\\ \frac {1} {\sqrt{6}} & \frac {-1} {\sqrt{2}} & \frac {1} {\sqrt{3}}\end{array} \right) \left( \begin{array}{ccc} \sqrt{3} & 0 \\ 0 & 1\\ 0 & 0 \end{array} \right) \left( \begin{array}{ccc} \frac {1} {\sqrt{2}}& \frac {1} {\sqrt{2}}\\ \frac {-1} {\sqrt{2}}& \frac {1} {\sqrt{2}}\end{array} \right)A=UΣVT=6162612102−1313−131300010(212−12121)
4. SVD的一些性质
上面几节我们对SVD的定义和计算做了详细的描述,似乎看不出我们费这么大的力气做SVD有什么好处。那么SVD有什么重要的性质值得我们注意呢?
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说:Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nTA_{m \times n} = U_{m \times m}\Sigma_{m \times n} V^T_{n \times n} \approx U_{m \times k}\Sigma_{k \times k}V^T_{k \times n}Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT
其中k要比n小很多,也就是一个大的矩阵A可以用三个小的矩阵Um×k,Σk×k,Vk×nTU_{m \times k},\Sigma_{k \times k} ,V^T_{k \times n}Um×k,Σk×k,Vk×nT来表示。如下图所示,现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。
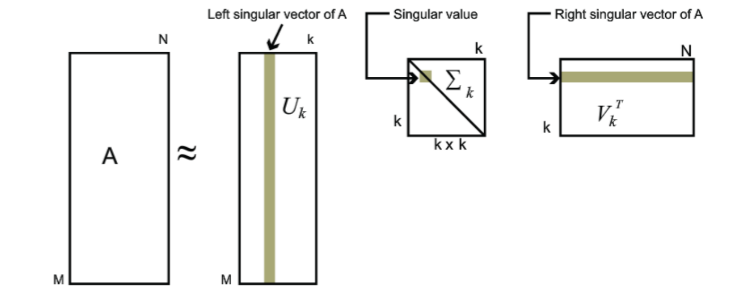
由于这个重要的性质,SVD可以用于PCA降维,来做数据压缩和去噪。也可以用于推荐算法,将用户和喜好对应的矩阵做特征分解,进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法,比如潜在语义索引(LSI)。下面我们就对SVD用于PCA降维做一个介绍。
5. SVD用于PCA
在主成分分析(PCA)原理总结中,我们讲到要用PCA降维,需要找到样本协方差矩阵XTXX^TXXTX的最大的d个特征向量,然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出,在这个过程中需要先求出协方差矩阵XTXX^TXXTX,当样本数多样本特征数也多的时候,这个计算量是很大的。
注意到我们的SVD也可以得到协方差矩阵XTXX^TXXTX最大的d个特征向量张成的矩阵,但是SVD有个好处,有一些SVD的实现算法可以不求先求出协方差矩阵XTXX^TXXTX,也能求出我们的右奇异矩阵V。也就是说,我们的PCA算法可以不用做特征分解,而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上,scikit-learn的PCA算法的背后真正的实现就是用的SVD,而不是我们我们认为的暴力特征分解。
另一方面,注意到PCA仅仅使用了我们SVD的右奇异矩阵,没有使用左奇异矩阵,那么左奇异矩阵有什么用呢?
假设我们的样本是m×nm \times nm×n的矩阵X,如果我们通过SVD找到了矩阵XXTXX^TXXT最大的d个特征向量张成的m×dm\times dm×d维矩阵U,则我们如果进行如下处理:Xd×n′=Ud×mTXm×nX'_{d\times n} = U_{d \times m}^TX_{m \times n}Xd×n′=Ud×mTXm×n
可以得到一个d×nd \times nd×n的矩阵X‘,这个矩阵和我们原来的m×nm\times nm×n维样本矩阵X相比,行数从m减到了k,可见对行数进行了压缩。也就是说,左奇异矩阵可以用于行数的压缩。相对的,右奇异矩阵可以用于列数即特征维度的压缩,也就是我们的PCA降维。
6. SVD小结
SVD作为一个很基本的算法,在很多机器学习算法中都有它的身影,特别是在现在的大数据时代,由于SVD可以实现并行化,因此更是大展身手。SVD的原理不难,只要有基本的线性代数知识就可以理解,实现也很简单因此值得仔细的研究。当然,SVD的缺点是分解出的矩阵解释性往往不强,有点黑盒子的味道,不过这不影响它的使用。
相关文章:

奇异值分解(SVD)原理与在降维中的应用
奇异值分解(SVD)原理与在降维中的应用 奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算…...

GDB调试程序
1.GDB 调试程序 GDB是GNU开源组织发布的一个强大的UNIX下的程序调试工具。在UNIX平台下做软件,GDB这个调试工具有比VC的图形化调试器更强大的功能。所谓“寸有所长,尺有所短”就是这个道理。 一般来说,GDB主要帮忙你完成下面四个方面的功能…...

五种IO模型
用户空间与内核空间 操作系统把内存空间划分成了两个部分:内核空间和用户空间。 为了保护内核空间的安全,操作系统一般都限制用户进程直接操作内核。 所以,当我们使用TCP发送数据的时候,需要先将数据从用户空间拷贝到内核空间&a…...

5 全面认识java的控制流程
全面认识java控制流程1.块作用域2.条件语句3.迭代语句3.1while语句3.2do-while语句3.3for语句3.4 for-in语法4.中断控制流程的语句4.1 return4.2 break和continue4.2.1 不带标签的break语句4.2.2 带标签的break语句4.2.3 continue语句4.3 goto()5.多重选择:switch语句1.块作用域…...

第二章 测验【嵌入式系统】
第二章 测验【嵌入式系统】前言推荐第二章 测验【嵌入式系统】最后前言 以下内容源自《嵌入式系统》 仅供学习交流使用 推荐 第一章 测验【嵌入式系统】 第二章 测验【嵌入式系统】 1单选题 32bit宽的数据0x12345678 在小端模式(Little-endian)模式…...

排序算法之插入排序
要考数据结构了,赶紧来复习一波排序算法 文章目录一、直接插入排序二、希尔排序一、直接插入排序 直接上主题 插排,揪出一个数,插入到原本已经有序的数组里面,如数组有n个数据,从0~n下标依次排列,先从左往…...
Kaggle实战入门:泰坦尼克号生生还预测
Kaggle实战入门:泰坦尼克号生生还预测1. 加载数据2. 特征工程3. 模型训练4. 模型部署泰坦尼克号(Titanic),又称铁达尼号,是当时世界上体积最庞大、内部设施最豪华的客运轮船,有“永不沉没”的美誉ÿ…...
)
【大汇总】11个Python开发经典错误(1)
“但是太阳,他每时每刻都是夕阳也都是旭日。当他熄灭着走下山去收尽苍凉残照之际,正是他在另一面燃烧着爬上山巅散烈烈朝晖之时。” --------史铁生《我与地坛》 🎯作者主页:追光者♂🔥 🌸个人简介:计算机专业硕士研究生💖、2022年CSDN博客之星人工智能领…...
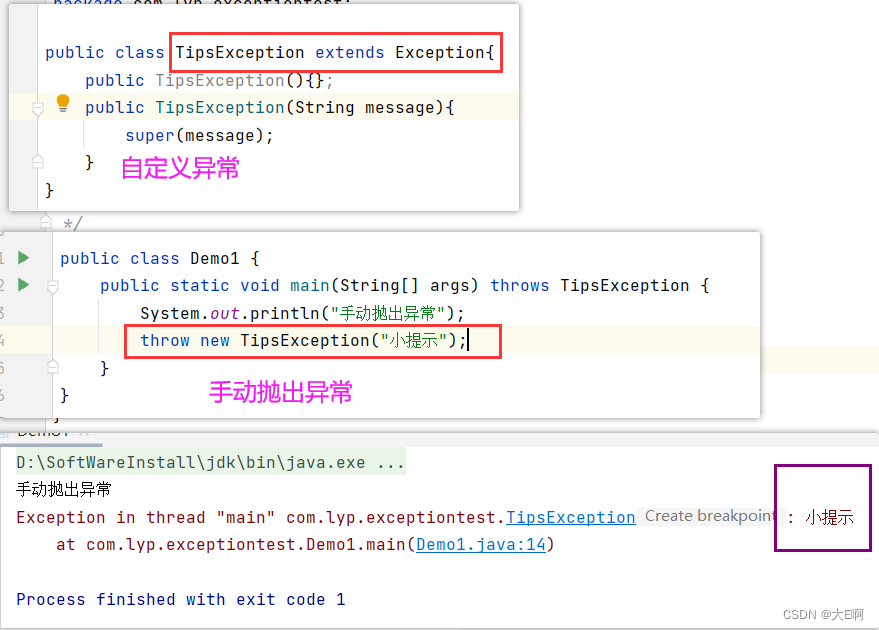
Java中的异常
程序错误一般分为三种:编译错误: 编写程序时没有遵循语法规则,编译程序能够自己发现错误并提示位置和原因。运行错误:程序在执行的时候运行环境发现了不能执行的操作。比如,JVM出错了,内存溢出等。逻辑错误…...

L2-022 重排链表 L2-002 链表去重
给定一个单链表 L1 →L2→⋯→L n−1 →L n ,请编写程序将链表重新排列为 L n →L 1 →L n−1 →L 2 →⋯。例如:给定L为1→2→3→4→5→6,则输出应该为6→1→5→2→4→3。 输入格式: 每个输入包含1个测试用例。每个测试用例第1行…...
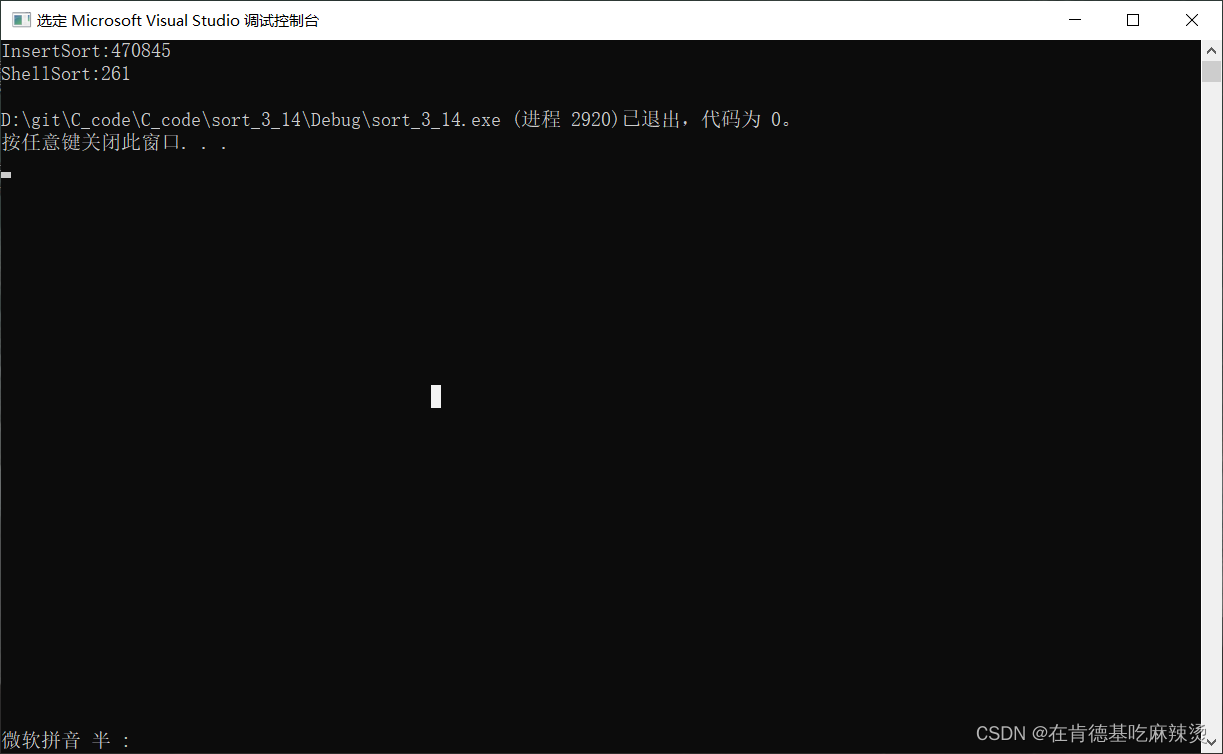
【手撕八大排序】——插入排序
文章目录插入排序概念插入排序分为2种一 .直接插入排序直接插入排序时间复杂度二.希尔排序希尔排序时间复杂度效率比较插入排序概念 直接插入排序是从一个有序的序列中选择一个合适的位置进行插入,这个合适的位置取决于是要升序排序还是降序排序。 每一次进行排序…...
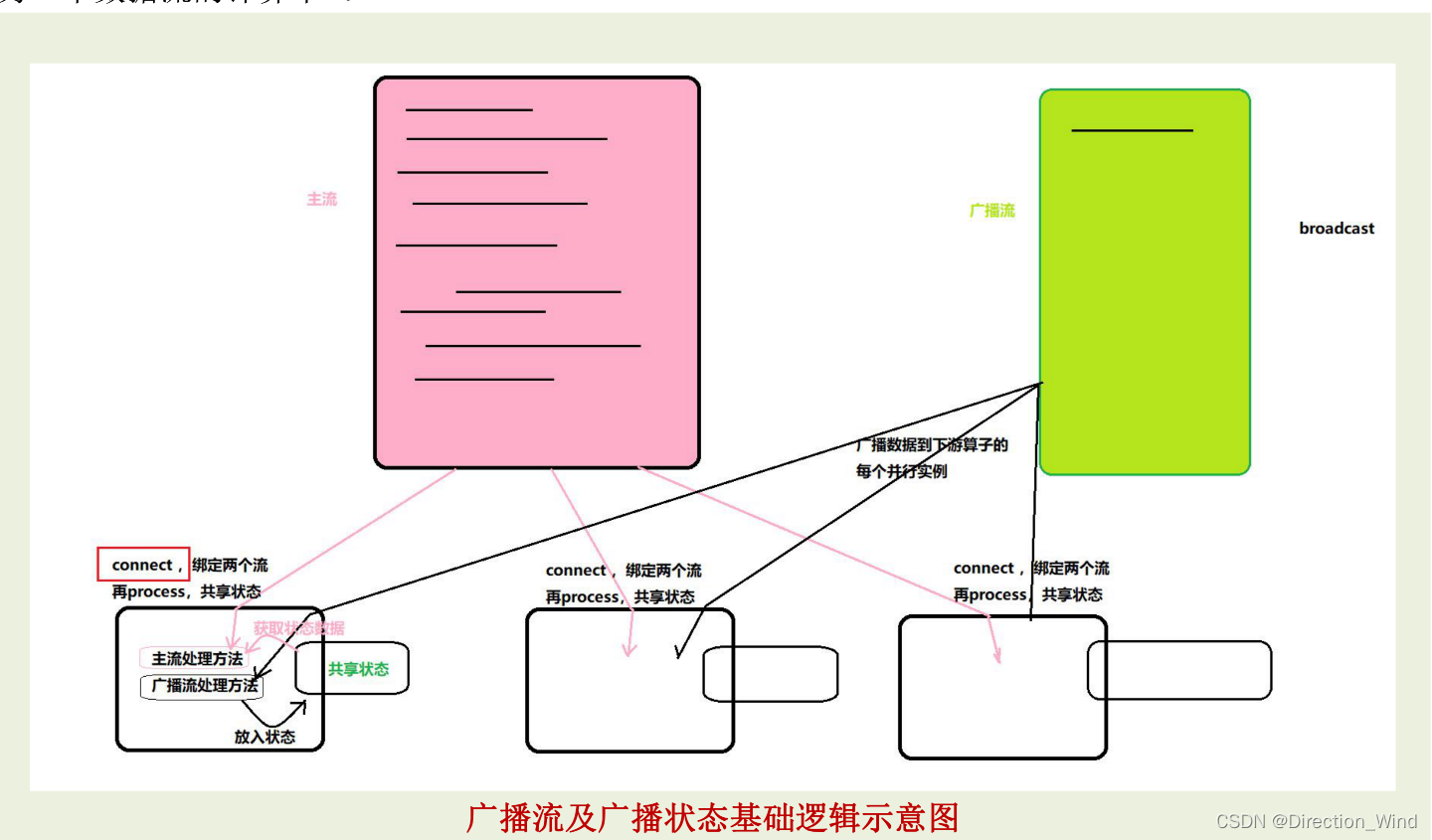
flink多流操作(connect cogroup union broadcast)
flink多流操作1 分流操作2 connect连接操作2.1 connect 连接(DataStream,DataStream→ConnectedStreams)2.2 coMap(ConnectedStreams → DataStream)2.3 coFlatMap(ConnectedStreams → DataStream)3 union操作3.1 uni…...

漫画:什么是快速排序算法?
这篇文章,以对话的方式,详细着讲解了快速排序以及排序排序的一些优化。 一禅:归并排序是一种基于分治思想的排序,处理的时候可以采取递归的方式来处理子问题。我弄个例子吧,好理解点。例如对于这个数组arr[] { 4&…...

vue 3.0组件(下)
文章目录前言:一,透传属性和事件1. 如何“透传属性和事件”2.如何禁止“透传属性和事件”3.多根元素的“透传属性和事件”4. 访问“透传属性和事件”二,插槽1. 什么是插槽2. 具名插槽3. 作用域插槽三,单文件组件CSS功能1. 组件作用…...
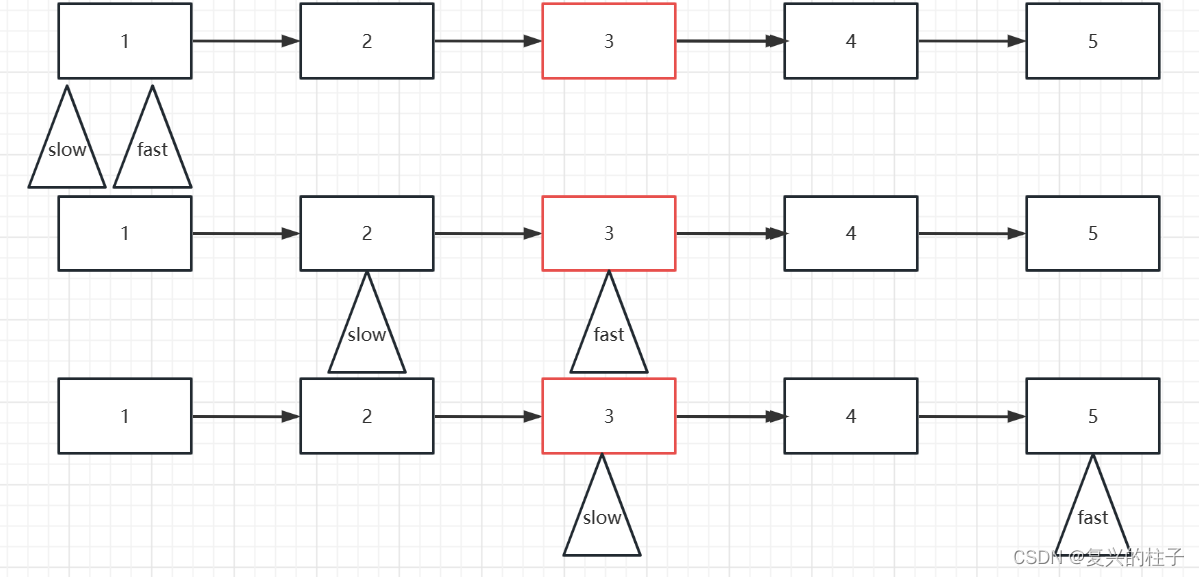
双指针 -876. 链表的中间结点-leetcode
开始一个专栏,写自己的博客 双指针,也算是作为自己的笔记吧! 双指针从广义上来说,是指用两个变量在线性结构上遍历而解决的问题。狭义上说, 对于数组,指两个变量在数组上相向移动解决的问题;对…...

Linux之运行级别
文章目录一、指定运行级别基本介绍CentOS7后运行级别说明一、指定运行级别 基本介绍 运行级别说明: 0:关机 1:单用户【找回丢失密码】 2:多用户状态没有网络服务 3:多用户状态有网络服务 4:系统未使用保留给用户 5:图形界面 6:系统重启 常用运行级别是3和5,也可以…...

python搭建web服务器
前言:相信看到这篇文章的小伙伴都或多或少有一些编程基础,懂得一些linux的基本命令了吧,本篇文章将带领大家服务器如何部署一个使用django框架开发的一个网站进行云服务器端的部署。 文章使用到的的工具 Python:一种编程语言&…...
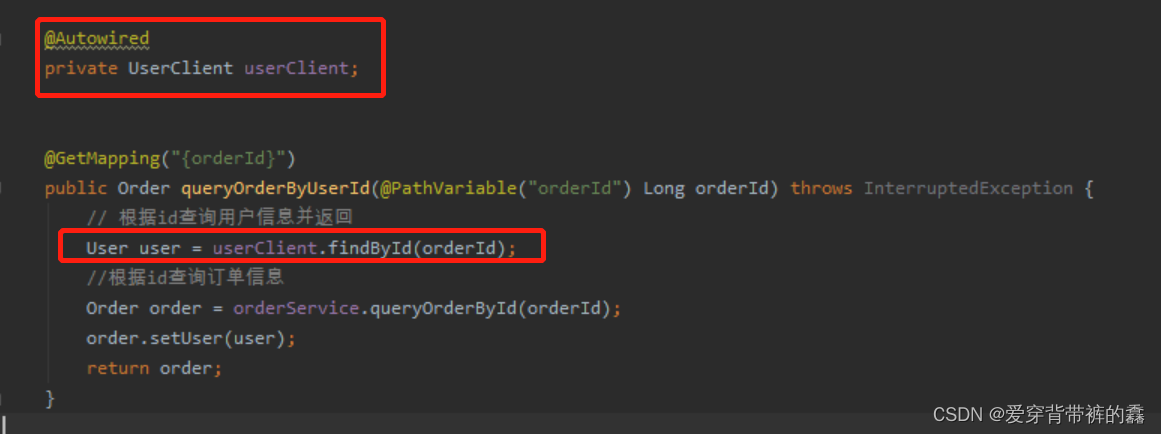
【SpringCloud】SpringCloud Feign详解
目录前言SpringCloud Feign远程服务调用一.远程调用逻辑图二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用四.构建Feign五.自定义Feign配置六.Feign配置日志七.Feign调优八.抽离Feign前言 微服务分解成多个不同的服务,那么多个服务之间怎么调用呢&…...

更改Hive元数据发生的生产事故
今天同事想在hive里用中文做为分区字段。如果用中文做分区字段的话,就需要更改Hive元 数据库。结果发生了生产事故。导致无法删除表和删除分区。记一下。 修改hive元数据库的编码方式为utf后可以支持中文,执行以下语句: alter table PARTITI…...
《Netty》从零开始学netty源码(八)之NioEventLoop.selector
目录java原生的WEPollSelectorImplnetty的SelectionKey容器SelectedSelectionKeySetnetty的SelectedSelectionKeySetSelectorSelectorTupleopenSelector每一个NioEventLoop配一个选择器Selector,在创建NioEventLoop的构造函数中会调用其自身方法openSelector获取sel…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
