数学建模学习（1）遗传算法

一、简介

        遗传算法（Genetic Algorithm, GA）是一种用于解决优化和搜索问题的进化算法。它基于自然选择和遗传学原理，通过模拟生物进化过程来寻找最优解。

        以下是遗传算法的主要步骤和概念：

• 初始化种群（Initialization）：随机生成一组可能的解（个体），形成初始种群。

• 适应度评估（Fitness Evaluation）：根据适应度函数评估每个个体的质量，即其解问题的效果。

• 选择（Selection）：根据适应度选择较优的个体进行繁殖。常见的选择方法包括轮盘赌选择、锦标赛选择和排序选择。

• 交叉（Crossover）：将两个个体的部分基因组合生成新的个体（子代）。交叉操作模拟生物的基因重组，常见的交叉方法有单点交叉和多点交叉。

• 变异（Mutation）：随机改变个体的部分基因，以增加种群的多样性，防止算法陷入局部最优。变异操作模拟生物的基因突变。

• 替换（Replacement）：将子代个体加入种群中，通常会替换掉适应度较低的个体，以保持种群规模恒定。

• 终止条件（Termination Condition）：当达到预定的终止条件时（如运行一定代数、适应度达到某个阈值），算法停止，输出最优解。

        遗传算法通常用于解决以下类型的问题：

• 优化问题，例如函数优化、路径优化（如旅行商问题）。
• 搜索问题，例如求解数独、密码破解。
• 机器学习中的参数优化，例如神经网络权重优化。

优点

• 遗传算法具有全局搜索能力，能够在较大的搜索空间中找到全局最优解。
• 适用于复杂的、多维的、非线性的优化问题。
• 不依赖于问题的具体数学性质，可以处理各种类型的目标函数和约束条件。

缺点

• 计算代价较高，尤其是适应度评估过程可能耗时。
• 需要精心设计适应度函数、选择方法、交叉和变异操作，才能获得好的效果。
• 对于某些问题，可能会收敛到局部最优解，而非全局最优解。

二、算法介绍 

（1）适应度函数

（2）轮盘赌选择

（3）锦标赛选择

（4）排序选择

 

（5）单点交叉 

应用场景

        单点交叉适用于问题规模较小或基因序列较短的情况。

        对于复杂问题或基因序列较长的情况，可以考虑多点交叉或均匀交叉等更复杂的交叉方法，以提高解的多样性和质量。

（6） 多点交叉

（7）均匀交叉 

 

 

（8）变异 

        通常设置较低的变异率（如 0.1% 到 1%）

三、遗传算法解TSP 

import copy
import random
import math
import numpy as np
import matplotlib.pyplot as pltN = 20000  # 最大迭代次数
city_num = 31
pop_size = 100  # 种群数量
pc = 0.8  # 交叉概率
pm = 0.05  # 变异概率# 城市坐标
city_position = [(1304, 2312), (3639, 1315), (4177, 2244), (3712, 1399), (3488, 1535),(3326, 1556), (3238, 1229), (4196, 1004), (4312, 790), (4380, 570),(3007, 1970), (2562, 1756), (2788, 1491), (2381, 1676), (1332, 695),(3715, 1678), (3918, 2179), (4061, 2370), (3780, 2212), (3676, 2578),(4029, 2838), (4263, 2931), (3429, 1908), (3507, 2367), (3394, 2643),(3439, 3201), (2935, 3240), (3140, 3550), (2545, 2357), (2778, 2826), (2370, 2975)]# 距离矩阵，城市之间的距离
dis = np.zeros((31, 31))
for i in range(31):for j in range(31):if i != j:dis[i][j] = ((city_position[i][0] - city_position[j][0]) ** 2 + (city_position[i][1] - city_position[j][1]) ** 2) ** 0.5# 初始化种群并去重
def init(pop_size, city_num):population = []while len(population) < pop_size:temp = random.sample(range(city_num), city_num)if temp not in population:population.append((temp))return population# 适应度函数
def fitness(population, dis):fitness = []for i in range(len(population)):distance = 0for j in range(city_num - 1):distance += dis[population[i][j]][population[i][j + 1]]distance += dis[population[i][-1]][population[i][0]]if distance == 0:f = float('inf')else:f = 1 / (distance ** 2)fitness.append(f)return fitness# 选择函数：轮盘赌选择
def select(population, fitness):index = random.randint(0, pop_size - 1)num = 0r = random.uniform(0, sum(fitness))for i in range(len(population)):num += fitness[i]if num >= r:index = ibreakreturn population[index]# 交叉函数
def cross(fa1, fa2):if random.random() < pc:chrom1 = fa1[:]chrom2 = fa2[:]cpoint1 = random.randint(0, city_num - 1)cpoint2 = random.randint(0, city_num - 1)if cpoint1 > cpoint2:temp = cpoint1cpoint1 = cpoint2cpoint2 = temptemp1 = []temp2 = []for i in range(cpoint1, len(chrom1)):temp1.append(chrom1[i])temp2.append(chrom2[i])for i in range(cpoint1, cpoint2 + 1):chrom1[i] = fa2[i]chrom2[i] = fa1[i]new_chrom1 = []new_chrom2 = []for i in range(cpoint2 + 1):new_chrom1.append(chrom1[i])new_chrom2.append(chrom2[i])new_chrom1.extend(temp1)new_chrom2.extend(temp2)ans1 = []ans2 = []for i in range(len(new_chrom1)):if new_chrom1[i] not in ans1:ans1.append(new_chrom1[i])for i in range(len(new_chrom2)):if new_chrom2[i] not in ans2:ans2.append(new_chrom2[i])return ans1, ans2else:return fa1[:], fa2[:]# 变异函数
def mutate(chrom):if random.random() < pm:mpoint1 = random.randint(0, city_num - 1)mpoint2 = random.randint(0, city_num - 1)temp = chrom[mpoint1]chrom[mpoint1] = chrom[mpoint2]chrom[mpoint2] = tempreturn chromdef show(lx, ly, fit_history):# 画出每代最好适应值的图像plt.plot(range(len(fit_history)), fit_history)plt.xlabel("Generation")plt.ylabel("Fitness")plt.show()# 画出最短路径大小的变化图a = []for i in range(len(fit_history)):a.append(math.sqrt(1 / fit_history[i]))plt.plot(range(len(a)), a)plt.xlabel("Generation")plt.ylabel("Best_path_size")plt.show()def best_show(x, y, Best_Fitness):# 定义两个子图fig, ax = plt.subplots(1, 2, figsize=(12, 5), facecolor='#ccddef')# 定义子图1标题ax[0].set_title("Best route")# 定义子图2标题ax[1].set_title("Best_Fitness Change Procession")# 画线ax[0].plot(x, y)# 画点（第一个子图）ax[0].scatter(x, y, color='r')# 画线（第二个子图）ax[1].plot(range(len(Best_Fitness)), [Best_Fitness[i] for i in range(len(Best_Fitness))])plt.show()# 主程序
if __name__ == '__main__':best_fit = 0.0ans = []best_path = []population = init(pop_size, city_num)  # 初始化种群，pop_size：种群个数for i in range(N):fit = fitness(population, dis)  # 计算适应度列表max_fit = max(fit)  # 因为适应度是采用距离和的平方的倒数，故最大的适应度代表距离最小max_index = fit.index(max_fit)  # 最大适应度的方案索引lx = []ly = []for j in population[max_index][:]:j = int(j)  # 保证整数lx.append(city_position[j][0])ly.append(city_position[j][1])if max_fit > best_fit:  # 假如路径更短best_fit = max_fit  # 修正了这里的错别字ans = population[max_index][:]x = copy.copy(lx)y = copy.copy(ly)best_path.append(best_fit)  # 记录适应度变化，为画图准备# 变异、交叉new_population = []n = 0while n < pop_size:p1 = select(population, fit)p2 = select(population, fit)while p2 == p1:p2 = select(population, fit)# 交叉chrom1, chrom2 = cross(p1, p2)# 变异chrom1 = mutate(chrom1)chrom2 = mutate(chrom2)new_population.append(chrom1)new_population.append(chrom2)n += 2population = new_populationprint("######################################################")print(f"第{i + 1}代的最优路径为：", ans)print("最短路径为：", (1 / best_fit) ** 0.5)show(lx,ly,best_path)x.append(x[0])y.append(y[0])best_show(x,y,best_path)

结果：

 

 

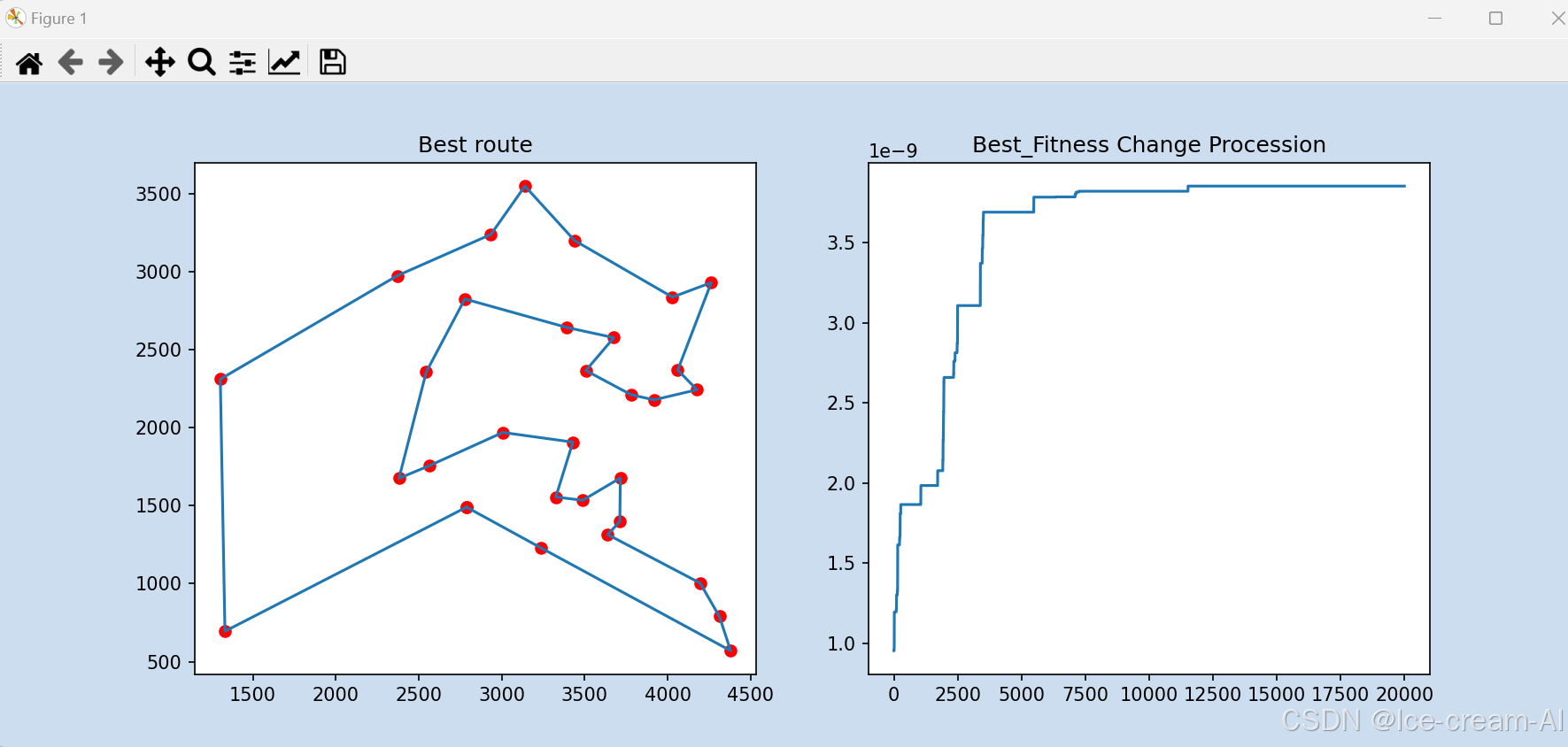
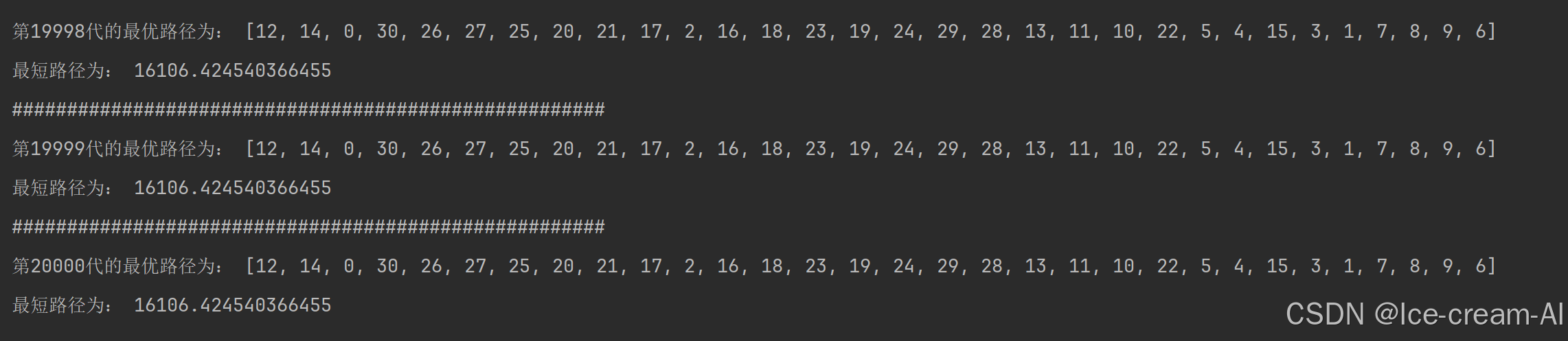
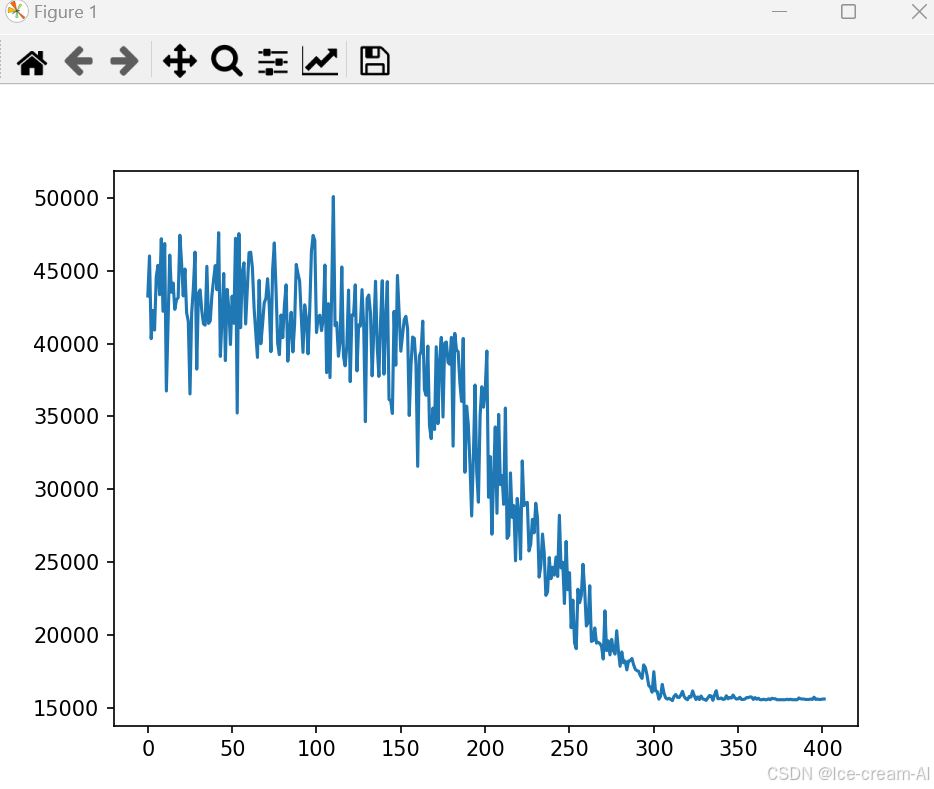
对比模拟退火算法的结果：

（以下是模拟退火算法的结果）