单调栈(随缘复习到了,顺手刷了)
也是不知道为什么突然又复习到单调栈了,所以顺手刷了三道题,总结一下
P6503 [COCI2010-2011#3] DIFERENCIJA


思路:这题是要求每个子区间里面的最大值和最小值的差,我们一开始想的必然是纯暴力呀,但是一看这数据,嚯!O(n^2)的时间复杂度,这不直接炸了,因此我们需要想一个O(n)的算法或者O(nlogn)的算法
我们再次分析题意,我们是否可以将题目转换一下,变成先求所有区间的最大值,然后再一起减去所有区间的最小值,然后就变成了求区间最值问题,那么就可以用单调栈了,时间复杂度为O(n)
我们用四个数组分别存储每个点的左边第一个比他大的,右边第一个比他大的,左边第一个比他小的,右边第一个比他小的,,然后求最大值就是每个最值只会出现( i - L)*(R - i )次
来看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
int a[300005];
int lmin[300005],rmin[300005],lmax[300005],rmax[300005];
stack<int> q;
void ini()
{while(!q.empty())q.pop();
}
signed main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){while(!q.empty()&&a[q.top()]<=a[i]){q.pop();}if(q.empty()){lmax[i]=0;}else{lmax[i]=q.top();}q.push(i);}ini();for(int i=1;i<=n;i++){while(!q.empty()&&a[q.top()]>=a[i]){q.pop();}if(q.empty()){lmin[i]=0;}else{lmin[i]=q.top();}q.push(i);}ini();for(int i=n;i>0;i--){while(!q.empty()&&a[q.top()]<a[i]){q.pop();}if(q.empty()){rmax[i]=n+1;}else{rmax[i]=q.top();}q.push(i);}ini();for(int i=n;i>0;i--){while(!q.empty()&&a[q.top()]>a[i]){q.pop();}if(q.empty()){rmin[i]=n+1;}else{rmin[i]=q.top();}q.push(i);}int ans=0;for(int i=1;i<=n;i++){ans+=a[i]*(i-lmax[i])*(rmax[i]-i);ans-=a[i]*(i-lmin[i])*(rmin[i]-i);}cout<<ans;return 0;
}P1823 [COI2007] Patrik 音乐会的等待

思路:这是一个队列,但是,我们要将其拆成一个链,也就是一开始的输入,输入进来一个就放一个进栈里面,我们要维护的是一个单调递增队列,每次进栈的时候也就是相邻的,只要栈不为空,都要统计数+1,然后就是如果存在栈弹出,也就说明ans++,但是有可能会出现等高的,所以我们还需要统计等高的人数,所以栈里面放的是pair数据,first用来存高度,second用来统计目前已经出现了多少个等高的
#include<bits/stdc++.h>
using namespace std;
#define int long longint n;
int h[500005];
pair<int,int> p;
stack< pair<int,int> >q;
int ans=0;
signed main()
{cin>>n;for(int i=1;i<=n;i++){cin>>h[i];}for(int i=1;i<=n;i++){p=make_pair(h[i],1);while(!q.empty()&&q.top().first<=h[i]){if(q.top().first==h[i]){p.second+=q.top().second;}ans+=q.top().second;q.pop();}if(!q.empty())ans++;q.push(p);}cout<<ans;return 0;
}Bindian Signalizing

思路:乍一看和上面的那个一样,但是有一个特判,就说第一座山,有可能会通过,反着来看看到后面的山,所以需要加上特判
#include<cstdio>
#include<stack>
using namespace std;int n;
int a[1000005];
int b[1000005];
int l[1000005];
int r[1000005];
int cnt[1000005];
stack<int>q;
int main()
{int maxn=0,flag=0;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);if(a[i]>maxn){maxn=a[i];flag=i;}}for(int i=0;i<=n;i++){b[i]=a[(flag+i)%n];}for(int i=1;i<=n;i++){while(!q.empty()&&b[q.top()]<=b[i]){q.pop();}if(q.empty())l[i]=0;elsel[i]=q.top();q.push(i);}while(!q.empty())q.pop();for(int i=n-1;i>=0;i--){while(!q.empty()&&b[q.top()]<b[i]){q.pop();}if(q.empty())r[i]=n;elser[i]=q.top();if(r[i]<n&&b[i]==b[r[i]]){cnt[i]=cnt[r[i]]+1;r[i]=r[r[i]];}q.push(i);}long long ans=0;for(int i=0;i<n;i++){ans+=cnt[i];if(b[i]<b[0]){ans+=2;if(l[i]==0&&r[i]==n){ans--;}}}printf("%lld\n",ans);return 0;
}
相关文章:

单调栈(随缘复习到了,顺手刷了)
也是不知道为什么突然又复习到单调栈了,所以顺手刷了三道题,总结一下 P6503 [COCI2010-2011#3] DIFERENCIJA 思路:这题是要求每个子区间里面的最大值和最小值的差,我们一开始想的必然是纯暴力呀,但是一看这数据&#…...
学习测试10-3自动化 web自动化
web自动化 chrome驱动下载地址: https://registry.npmmirror.com/binary.html?pathchromedriver/ https://googlechromelabs.github.io/chrome-for-testing/#stable观察Google版本,下相应的驱动 运行代码试试,成功Google就会弹出 from se…...
安防视频监控EasyCVR视频汇聚平台修改配置后无法启动的原因排查与解决
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台基于云边端一体化架构,兼容性强、支持多协议接入,包括国标GB/T 28181协议、部标JT808、GA/T 1400协议、RTMP、RTSP/Onvif协议、海康Ehome、海康SDK、大华SDK、华为SDK、宇视SDK、乐橙SDK、萤石云SD…...

爬虫学习2:爬虫爬取网页的信息与图片的方法
爬虫爬取网页的信息与图片的方法 爬取人物信息 import requestshead {"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/126.0.0.0 Safari/537.36 Edg/126.0.0.0" } # 这是get请求带参数的模式…...

MySQL定时备份数据,并上传到oss
1.环境准备 1.安装阿里云的ossutil 2.安装mysql 2.编写脚本 脚本内容如下 #!/bin/bash # 数据库的配置信息,根据自己的情况进行填写 db_hostlocalhost db_usernameroot db_passwordroot db_namedb_root # oss 存贮数据的bucket地址 bucket_namerbsy-backup-buck…...
)
极速删除 node_modules 仅3 秒()
今天教大家如何快速删除 node_modules 依赖的一个小秘诀,告别繁琐!!! 前言 作为前端开发者,相信大家都曾经历过删除 node_modules 文件夹时的漫长等待。 尤其是在处理那些依赖库繁多的项目时,删除操作…...

vue this.$refs 动态拼接
业务需要,refs是不固定的 <vxe-grid refgridWarehouse v-bind"gridWarehouseOptions" v-if"tableHeight" :height"tableHeight":expand-config"{iconOpen: vxe-icon-square-minus, iconClose: vxe-icon-square-plus}"c…...

一次搞定!中级软件设计师备考通关秘籍
大家好,我是小欧! 今天我们来聊聊软考这个话题。要是你准备参加计算机技术与软件专业技术资格(软考),那么这篇文章就是为你量身定做的。话不多说,咱们直接进入正题。 什么是软考? 软考…...

第十六讲 python中的序列-列表简介-特点-常用方法-创建-添加-删除-访问-切片-排序-复制-反转
目录 1. 序列的本质和内存结构 2.列表 2.1 列表简介 2.2 列表的特点 2.3 列表对象的常用方法大全: 2.4 列表的创建 2.4.1 使用方括号 [] 2.4.2 使用 list() 函数 2.4.3 使用 range() 函数 2.4.3.1 range的基本用法 2.4.3.2 返回值 2.4.3.3 range的使用例子 2.4.3.4 range的使…...

大模型日报 2024-07-22
大模型日报 2024-07-22 大模型资讯 谷歌将在ICML 2024展示机器学习研究成果 摘要: 谷歌研究人员将在ICML 2024会议上展示他们在机器学习领域的探索,从理论到应用,构建解决深层问题的ML系统。 代理符号学习:优化AI系统符号组件的框架 摘要: 大…...

Electron 的open-file事件
在 Electron 中,open-file 事件是一个重要的事件,它允许开发者在应用程序已经运行的情况下,通过文件打开请求(如双击文件或在命令行中使用 open 命令打开文件)来捕获文件路径。以下是对 open-file 事件的详细解析: 触发条件 应用已经打开。用户通过双击与应用程序关联的…...

前端面试 vue 接口权限控制
接口权限目前一般采用jwt的形式来验证,没有通过的话一般返回401,跳转到登录页面重新进行登录 对于 jwt的理解 (前端接口权限的控制主要通过接口权限配置和JWT(Json Web Token)技术来实现。 首先,…...

【DevOps系列】构建Devops系统
开始介绍 那就着手开始干吧。先介绍一下我们的工具链。 主要工具:GitHub、Jenkins、Kubernetes、Ansible、Prometheus和JMeter 着手动 1. 设置GitHub作为源代码仓库 登录GitHub: 打开浏览器并访问 https://github.com,使用您的GitHub账户登录。 创建…...
ABAP打印WORD的解决方案
客户要求按照固定格式输出到WORD模板中,目前OLE和DOI研究了均不太适合用于这种需求。 cl_docx_document类可以将WORD转化为XML文件,利用替换字符串方法将文档内容进行填充同 时不破坏WORD现有格式。 首先需要将WORD的单元格用各种预定义的字符进行填充,为后续替换作准备…...
emr部署hive并适配达梦数据库
作者:振鹭 一、达梦 用户、数据库初始化 1、创建hive的元数据库 create tablespace hive_meta datafile /dm8/data/DAMENG/hive_meta.dbf size 100 autoextend on next 1 maxsize 2048;2、创建数据库的用户 create user hive identified by "hive12345&quo…...

王春城:怎么用精益思维重塑企业战略规划格局?
当下,企业战略规划的灵活性和适应性变得至关重要。传统的战略规划方法往往过于僵化和静态,难以应对市场的不确定性和变化。因此,引入精益思维来重塑企业战略规划格局,成为了许多企业寻求突破和创新的途径。具体步骤如深圳天行健企…...
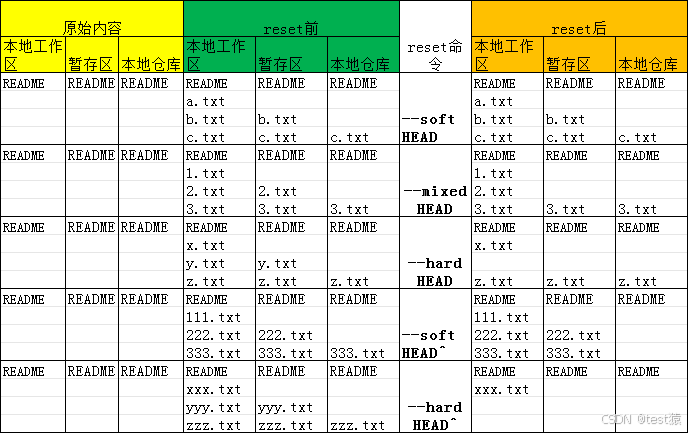
git reset
git reset [--soft | --mixed | --hard] [HEAD] 表格版 原始内容reset前reset命令reset后本地工作区暂存区本地仓库本地工作区暂存区本地仓库本地工作区暂存区本地仓库READMEREADMEREADMEREADMEREADMEREADME--soft HEADREADMEREADMEREADMEa.txta.txtb.txtb.txtb.txtb.txtc.tx…...

E17.【C语言】练习:sizeof和strlen的辨析
先回顾http://t.csdnimg.cn/aYHl6 1. char acX[] "abcdefg"; char acY[] { a,b,c,d,e,f,g}; 以下说法正确的是( ) A.数组acX和数组acY等价 B.数组acX和数组acY的长度相同 C.sizeof(acX)>sizeof (acY) D.strlen (acX)>strlen (acY) 分析:…...

便携气象站:科技助力气象观测
在科技飞速发展的今天,便携气象站以其轻便、高效、全面的特点,正逐渐改变着气象观测的传统模式。这款小巧而强大的设备,不仅为气象学研究和气象灾害预警提供了有力支持,更为户外活动、农业生产等领域带来了诸多便利。 便携气象站是…...

php 存储复杂的json格式查询(如:经纬度)
在开发中,有时我们可能存了一些复杂json格式不知道怎么查。我这里提供给大家参考下: 一、先上表数据格式(location字段的possiton经纬度以逗号分开的) {"title":"澳海文澜府","position":"11…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
