排序算法与复杂度介绍
1. 排序算法
1.1 排序算法介绍
排序也成排序算法(Sort Algorithm),排序是将一组数据,依照指定的顺序进行排序的过程
1.2 排序的分类
1、内部排序:
指将需要处理的所有数据都加载到**内部存储器(内存)中进行排序。
2、外部排序
数据量过大,无法全部加载到内存中,需要借助外部存储(文件等)**进行排序
3、常见的排序算法分类: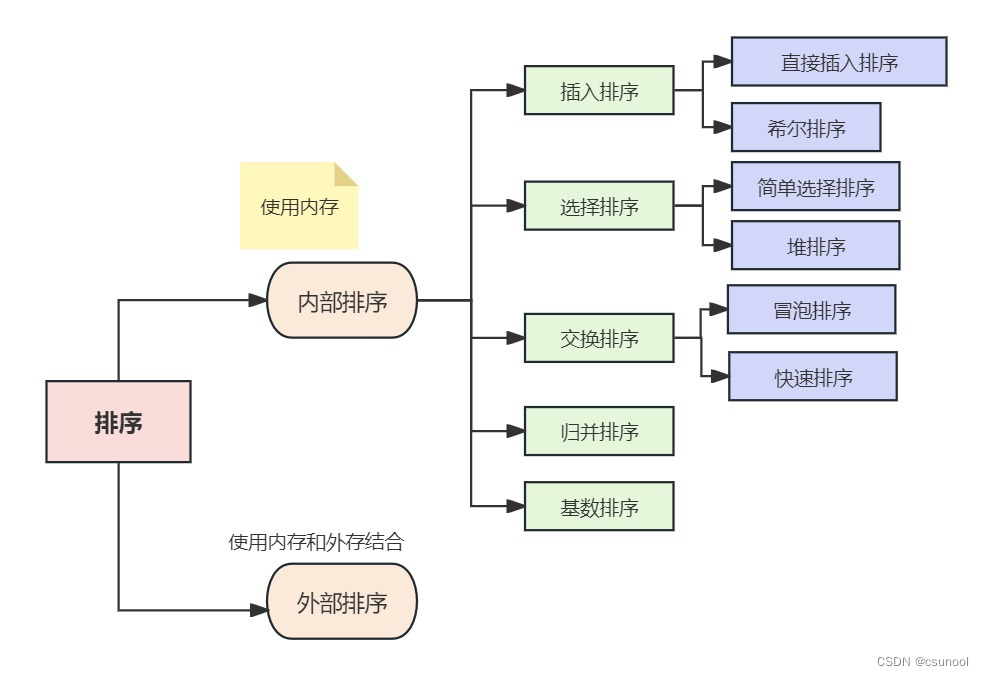
4、算法时间复杂度
度量一个程序(算法)执行时间的两种方法
(1)事后统计的方法
这种方法可行,但是有两个问题:一是想对设计的算法的运行性能进行评测,需要实际运行该程序;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素,这种方式,要在同一个计算机的相同状态下运行,才能比较哪个算法速度更快。
(2)事前估算的方法
通过分析某个算法的时间复杂度来判断哪个算法更优。
1.3 算法的时间复杂度
1、时间频度:一个算法执行的时间与算法中语句执行的次数成正比,哪个算法中语句执行次数多,它花费的时间就多。一个算法中语句执行次数称为语句频度或者时间频度,记为T(n)
2、举例说明—基本案例
比如计算1-100所有数字之和,我们设计两种算法
int total = 0 ;
int end = 100 ;
// 使用for循环计算
for(int i = 1; i < end; i++) {total += i;
}
T(n) = n + 1;// 直接计算
total = (1+end) * end/2
T(n) = 1;
3、时间复杂度
1、一般情况下算法中的基本操作语句的重复执行次数是问题规模n的某个函数,用T(n)表示,若有,某个辅助函数 f(n) ,使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于0的常数,则称f(n)是T(n)的同数量级函数。记作T(n) = O(f(n)),称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。
2、T(n)不同,但是时间复杂度可能相同。如: T(n) = n² + 7n+ 6 与 T(n ) = 3n² + 2n+ 2 他们的T(n)不同,但是时间复杂度相同,都为O(n²)。
3、计算时间复杂度的方法:
用常数1 代替运行时间中的所有加法常数 T(n) = n² + 7n+ 6 → T(n) = n² + 7n+ 1
修改后的运行次数函数中,只保留最高阶项 T(n) = n² + 7n+ 1 → T(n) = n²
去除最高阶项的系数 T(n) = n² → T(n) = n² → O(n²)
1.4 常见的时间复杂度
1、常数阶 O(1)
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
2、对数阶 O(㏒2n)
int i = 1;
while (i < n) {
i = i * 2;
}
3、线性阶 O(n)
for(int i = 0; i <= n; i++) {j = i;j++ ;
}
4、线性对数阶O(n㏒2n)
for( m = 1; m < n; m++) {i = 1;while (i<n) {i = i * 2;}
}
5、平方阶 O(n²)
for(x=1; x<n; x++) {for(i=1; i<n; i++) {j = i;j++;}
}
6、立方阶 O(n³)
7、k次方阶 O(n∧k)
参考上面的O(n²)去理解就好了,O(n³) 相当于3层n循环,其他的类似
8、指数阶 O(2∧n)
说明:
1、 常见的算法时间复杂度由小到大依次为: O(1) < O(㏒2n) < O(n) < O(n㏒2n) < O(n²) < O(n³) < O(n∧k) < O(2∧n),随着问题规模n的不断增大,算法的执行效率越低
2、我们应该尽可能避免使用指数阶的算法
1.5 平均时间复杂度和最坏时间复杂度
1、平均时间复杂度是指所有的可能的输入实例均以等概率出现的情况下,该算法运行的时间
2、最坏情况下的时间复杂度称为最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。
3、平均时间复杂度和最坏时间复杂度是否一致,和算法有关。
1.6 算法的空间复杂度简介
基本介绍
1、类似于时间复杂度的讨论,一个算法的空间复杂度(space complexity) 定义为该算法所耗费的存储空间,它也是问题规模n的函数。
2、空间复杂度(space complexity) 是对一个算法在运行过程中临时占用存储空间大小的度量。有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元,例如快速排序和归并排序算法就属于这种情况。
3、在做算法分析时,主要讨论的是时间复杂度。从用户体验上看,更看重程序运行的速度。一些缓存产品(redis、memcache)和算法(基数排序)本质就是用空间换时间。
相关文章:

排序算法与复杂度介绍
1. 排序算法 1.1 排序算法介绍 排序也成排序算法(Sort Algorithm),排序是将一组数据,依照指定的顺序进行排序的过程 1.2 排序的分类 1、内部排序: 指将需要处理的所有数据都加载到**内部存储器(内存&am…...
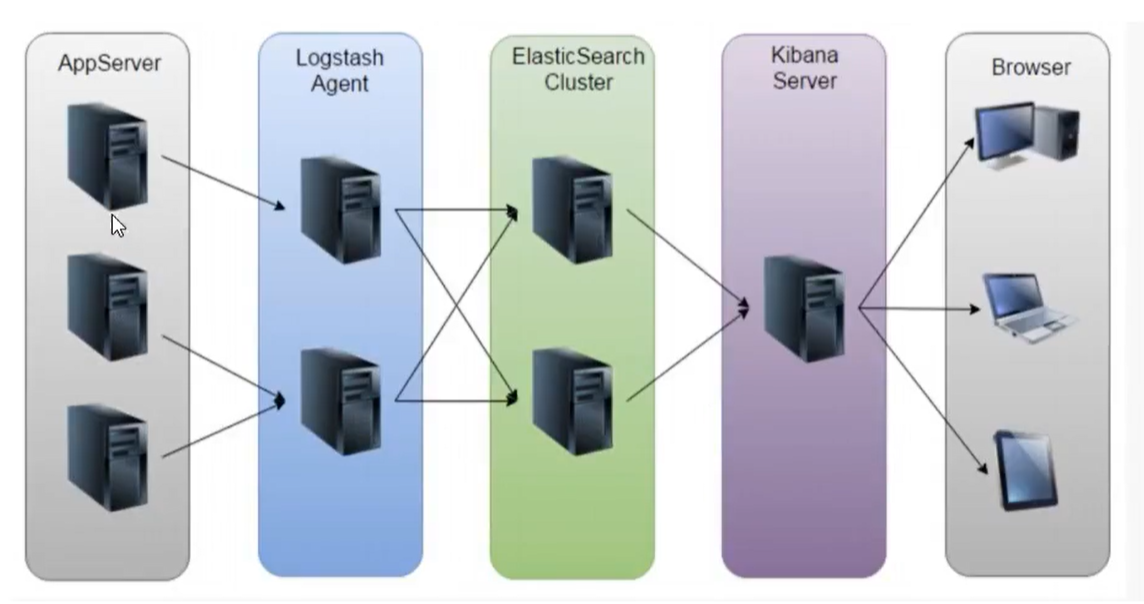
Kafka介绍及Go操作kafka详解
文章目录 Kafka介绍及Go操作kafka详解项目背景解决方案面临的问题业界方案ELKELK方案的问题日志收集系统架构设计架构设计组件介绍将学到的技能消息队列的通信模型点对点模式 queue发布/订阅 topicKafka介绍Kafka的架构图工作流程选择partition的原则ACK应答机制Topic和数据日志…...

DAY05 CSS
文章目录 1 CSS选择器(Selectors)8. 后代(包含)选择器9. 直接子代选择器10. 兄弟选择器11. 相邻兄弟选择器12. 属性选择器 2 伪元素3 CSS样式优先级1. 相同选择器不同样式2. 相同选择器相同样式3. 继承现象4. 选择器不同权值的计算 4 CSS中的值和单位1. 颜色表示法2. 尺寸表示法…...

HTTPS 的加密过程 详解
HTTP 由于是明文传输,所以安全上存在以下三个风险: 窃听风险,比如通信链路上可以获取通信内容。篡改风险,比如通信内容被篡改。冒充风险,比如冒充网站。 HTTPS 在 HTTP 与 TCP 层之间加入了 SSL/TLS 协议,…...

spring整合mybatis,junit纯注解开发(包括连接druid报错的所有解决方法)
目录 Spring整合mybatis开发步骤 第一步:创建我们的数据表 第二步:编写对应的实体类 第三步:在pom.xml中导入我们所需要的坐标 spring所依赖的坐标 mybatis所依赖的坐标 druid数据源坐标 数据库驱动依赖 第四步:编写SpringC…...

ClusterIP、NodePort、LoadBalancer 和 ExternalName
Service 定义 在 Kubernetes 中,由于Pod 是有生命周期的,如果 Pod 重启它的 IP 可能会发生变化以及升级的时候会重建 Pod,我们需要 Service 服务去动态的关联这些 Pod 的 IP 和端口,从而使我们前端用户访问不受后端变更的干扰。 …...

【Day1415】Bean管理、SpringBoot 原理、总结、Maven 高级
0 SpringBoot 配置优先级 从上到下 虽然 springboot 支持多种格式配置文件,但是在项目开发时,推荐统一使用一种格式的配置 (yml是主流) 1 Bean管理 1.1 从 IOC 容器中获取 Bean 1.2 Bean 作品域 可以通过注解 Scope("proto…...

Git之repo sync -c与repo sync -dc用法区别(四十八)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

vite + vue3 + uniapp 项目从零搭建
vite + vue3 + uniapp 项目从零搭建 1、创建项目1.1、创建Vue3/vite版Uniapp项目1.2、安装依赖1.3、运行项目2、弹出 用户隐私保护提示 方法2.1、更新用户隐私保护指引 和 修改配置文件2.2、授权结果处理方法3、修改`App.vue`文件内容4、处理报`[plugin:uni:mp-using-component…...

在CentOS中配置三个节点之间相互SSH免密登陆
在CentOS中配置三个节点(假设分别为node1、node2、node3)两两之间相互SSH免密登陆,可以按照以下步骤进行: 一、生成密钥对 在所有节点上生成密钥对: 在每个节点(node1、node2、node3)上执行以…...

arm 内联汇编基础
一、 Arm架构寄存器体系熟悉 基于arm neon 实现的代码有 intrinsic 和inline assembly 两种实现。 1.1 通用寄存器 arm v7 有 16 个 32-bit 通用寄存器,用 r0-r15 表示。 arm v8 有 31 个 64-bit 通用寄存器,用 x0-x30 表示,和 v7 不一样…...

Java语言程序设计——篇五(1)
数组 概述数组定义实例展示实战演练 二维数组定义数组元素的使用数组初始化器实战演练:矩阵计算 💫不规则二维数组实战演练:杨辉三角形 概述 ⚡️数组是相同数据类型的元素集合。各元素是有先后顺序的,它们在内存中按照这个先后顺…...

【香橙派开发板测试】:在黑科技Orange Pi AIpro部署YOLOv8深度学习纤维分割检测模型
文章目录 🚀🚀🚀前言一、1️⃣ Orange Pi AIpro开发板相关介绍1.1 🎓 核心配置1.2 ✨开发板接口详情图1.3 ⭐️开箱展示 二、2️⃣配置开发板详细教程2.1 🎓 烧录镜像系统2.2 ✨配置网络2.3 ⭐️使用SSH连接主板 三、…...

集成学习在数学建模中的应用
集成学习在数学建模中的应用 一、集成学习概述(一)基知(二)相关术语(三)集成学习为何能提高性能?(四)集成学习方法 二、Bagging方法(一)装袋&…...

WebKit 的 Web SQL 数据库:现代浏览器的本地存储解决方案
WebKit 的 Web SQL 数据库:现代浏览器的本地存储解决方案 随着Web应用的不断发展,对本地存储的需求也日益增加。WebKit作为许多现代浏览器的核心引擎,提供了一种强大的本地存储解决方案:Web SQL 数据库。本文将详细探讨Web SQL 数…...

Yolo-World网络模型结构及原理分析(三)——RepVL-PAN
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言1. 网络结构2. 特征融合3. 文本引导(Text-guided)4. 图像池化注意力(Image-Pooling Attention)5. 区域文本匹配&…...

代码随想录——一和零(Leetcode474)
题目链接 0-1背包 class Solution {public int findMaxForm(String[] strs, int m, int n) {// 本题m,n为背包两个维度// dp[i][j]:最多右i个0和j个1的strs的最大子集大小int[][] dp new int[m 1][n 1];// 遍历strs中字符串for(String str : strs){int num0 …...
)
力扣题解(组合总和IV)
377. 组合总和 Ⅳ 给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。 题目数据保证答案符合 32 位整数范围。 思路: 本题实质上是给一些数字,让他们在满足和是targ…...

Postgresql主键自增的方法
Postgresql主键自增的方法 一.方法(一) 使用 serial PRIMARY KEY 插入数据 二.方法(二) 🎈边走、边悟🎈迟早会好 一.方法(一) 使用 serial PRIMARY KEY 建表语句如下…...

【源码阅读】Sony的go breaker熔断器源码探究
文章目录 背景源码分析总结 背景 在微服务时代,服务和服务之间调用、跨部门调用都是很常见的事,但这些调用都存在很多不确定因素,如核心服务A依赖的部门B服务挂掉了,那么A本身的功能将会受到直接的影响,而这些都会影响…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
