十大排序的稳定性和时间复杂度
十大排序算法的稳定性和时间复杂度是数据结构和算法中的重要内容。
以下是对这些算法的稳定性和时间复杂度的详细分析:
稳定性
稳定性指的是排序算法在排序过程中是否能够保持相等元素的原始相对顺序。根据这个定义,我们可以将排序算法分为稳定排序和不稳定排序两大类。
稳定排序算法:
- 冒泡排序:通过相邻元素的比较和交换进行排序,相同元素在排序过程中不会改变相对位置。
- 插入排序:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。相同元素会保持原有的顺序。
- 归并排序:采用分治策略,将序列分成多个子序列,分别排序后再合并。合并过程中会保证相同元素的顺序。
- 计数排序:非比较排序算法,通过统计每个元素的出现次数来确定其在排序后数组中的位置。相同元素会按照它们在原数组中的顺序排列。
- 桶排序(在特定条件下):如果每个桶内部使用稳定的排序算法,则整个桶排序也是稳定的。
- 基数排序:按照低位先排序,然后收集;再按照高位排序,然后再收集。相同元素在排序过程中会保持原有的顺序。
不稳定排序算法:
- 选择排序:通过选择剩余未排序部分的最小(或最大)元素,与未排序部分的第一个元素交换位置。这个过程中,相同元素的相对位置可能会发生改变。
- 希尔排序:是插入排序的一种更高效的改进版本,通过不同步长的插入排序来加快排序速度。但由于不同步长的插入排序可能会导致相同元素的相对位置发生变化,因此希尔排序是不稳定的。
- 快速排序:通过选择一个基准元素,将数组分为小于和大于基准元素的两个部分,然后递归地对这两部分进行排序。这个过程中,相同元素的相对位置可能会发生改变。
- 堆排序:通过构建二叉堆来进行排序。在堆的调整过程中,相同元素的相对位置可能会发生改变。
- 时间复杂度
时间复杂度和稳定性
时间复杂度是衡量算法执行时间随输入规模增长而增长的速率的一个指标。以下是十大排序算法的平均、最好和最坏情况下的时间复杂度:
排序算法 平均时间复杂度 最好时间复杂度 最坏时间复杂度
冒泡排序 O(n^2) O(n) O(n^2)
选择排序 O(n^2) O(n^2) O(n^2)
插入排序 O(n^2) O(n) O(n^2)
希尔排序 O(n log n) O(nlogn) O(n^2)
归并排序 O(n log n) O(n log n) O(n log n)
快速排序 O(n log n) O(n log n) O(n^2)
堆排序 O(n log n) O(n log n) O(n log n)
计数排序 O(n + k) O(n + k) O(n + k)
桶排序 O(n + k) O(n) O(n^2)
基数排序 O(d(n + k)) O(d(n + k)) O(d(n + k))
其中,n 是数组的长度,k 是整数的范围(对于计数排序和桶排序),d 是数字的位数(对于基数排序)。。
相关文章:

十大排序的稳定性和时间复杂度
十大排序算法的稳定性和时间复杂度是数据结构和算法中的重要内容。 以下是对这些算法的稳定性和时间复杂度的详细分析: 稳定性 稳定性指的是排序算法在排序过程中是否能够保持相等元素的原始相对顺序。根据这个定义,我们可以将排序算法分为稳定排序和…...
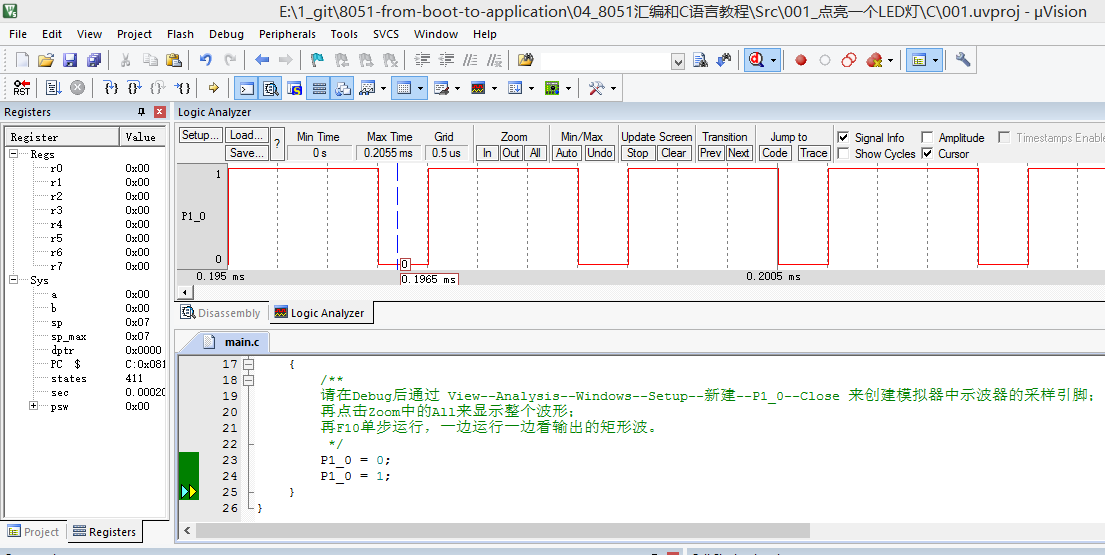
【系列教程之】1、点亮一个LED灯
1、点亮一个LED灯 作者将狼才鲸创建日期2024-07-23 CSDN教程目录地址:【目录】8051汇编与C语言系列教程本Gitee仓库原始地址:才鲸嵌入式/8051_c51_单片机从汇编到C_从Boot到应用实践教程 本源码包含C语言和汇编工程,能直接在电脑中通过Keil…...

搜维尔科技:Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作
Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作 搜维尔科技:Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作...

机器学习 | 阿里云安全恶意程序检测
目录 一、数据探索1.1 数据说明1.2 训练集数据探索1.2.1 数据特征类型1.2.2 数据分布1.2.3 缺失值1.2.4 异常值1.2.5 标签分布探索 1.3 测试集探索1.3.1 数据信息1.3.2 缺失值1.3.3 数据分布1.3.4 异常值 1.4 数据集联合分析1.4.1 file_id 分析1.4.2 API 分析 二、特征工程与基…...

python打包exe文件-实现记录
1、使用pyinstaller库 安装库: pip install pyinstaller打包命令标注主入库程序: pyinstaller -F.\程序入口文件.py 出现了一个问题就是我在打包运行之后会出现有一些插件没有被打包。 解决问题: 通过添加--hidden-importcomtypes.strea…...

基本的DQL语句-单表查询
一、DQL语言 DQL(Data Query Language 数据查询语言)。用途是查询数据库数据,如SELECT语句。是SQL语句 中最核心、最重要的语句,也是使用频率最高的语句。其中,可以根据表的结构和关系分为单表查询和多 表联查。 注意:所有的查询…...

Vue3 对比 Vue2
相关信息简介2020年9月18日,Vue.js发布3.0版本,代号:One Piece(海贼王) 2 年多开发, 100位贡献者, 2600次提交, 600次 PR、30个RFC Vue3 支持 vue2 的大多数特性 可以更好的支持 Typescript,提供了完整的…...

2024中国大学生算法设计超级联赛(1)
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,彩笔ACMer一枚。 🏀所属专栏:杭电多校集训 本文用于记录回顾总结解题思路便于加深理解。 📢📢📢传送门 A - 循环位移解…...

offer题目51:数组中的逆序对
题目描述:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。例如,在数组{7,5,6,4}中,一共存在5个逆序对,分别是(7…...

45、PHP 实现滑动窗口的最大值
题目: PHP 实现滑动窗口的最大值 描述: 给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。 例如: 如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3, 那么一共存在6个滑动窗口, 他们的最大值…...

【计算机视觉】siamfc论文复现实现目标追踪
什么是目标跟踪 使用视频序列第一帧的图像(包括bounding box的位置),来找出目标出现在后序帧位置的一种方法。 什么是孪生网络结构 孪生网络结构其思想是将一个训练样本(已知类别)和一个测试样本(未知类别)输入到两个CNN(这两个CNN往往是权值共享的)中࿰…...

数学建模学习(111):改进遗传算法(引入模拟退火、轮盘赌和网格搜索)求解JSP问题
文章目录 一、车间调度问题1.1目前处理方法1.2简单案例 二、基于改进遗传算法求解车间调度2.1车间调度背景介绍2.2遗传算法介绍2.2.1基本流程2.2.2遗传算法的基本操作和公式2.2.3遗传算法的优势2.2.4遗传算法的不足 2.3讲解本文思路及代码2.4算法执行结果: 三、本文…...

Golang | Leetcode Golang题解之第241题为运算表达式设计优先级
题目: 题解: const addition, subtraction, multiplication -1, -2, -3func diffWaysToCompute(expression string) []int {ops : []int{}for i, n : 0, len(expression); i < n; {if unicode.IsDigit(rune(expression[i])) {x : 0for ; i < n &…...

Unity客户端接入原生Google支付
Unity客户端接入原生Google支付 1. Google后台配置2. 开始接入Java部分C#部分Lua部分 3. 导出工程打包测试参考踩坑注意 1. Google后台配置 找到内部测试(这个测试轨道过审最快),打包上传,这个包不需要接入支付,如果已…...

Spring Cloud之五大组件
Spring Cloud 是一系列框架的有序集合,为开发者提供了快速构建分布式系统的工具。这些组件可以帮助开发者做服务发现,配置管理,负载均衡,断路器,智能路由,微代理,控制总线等。以下是 Spring Cl…...
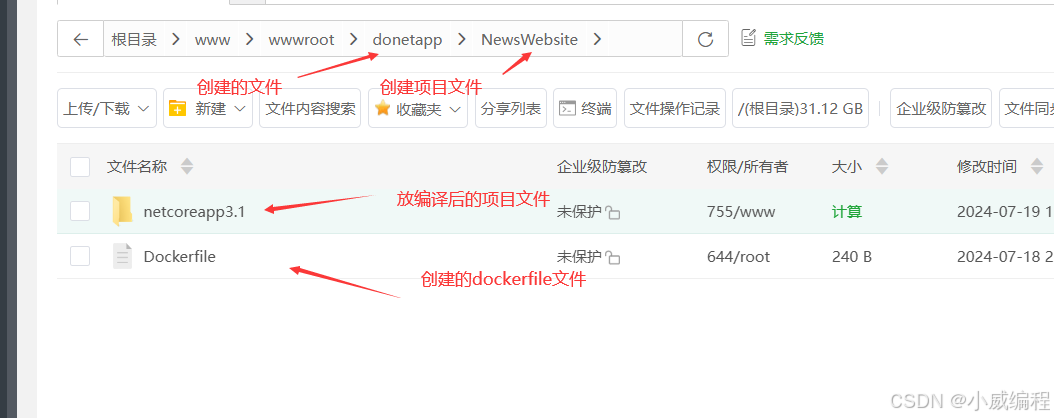
在 CentOS 7 上安装 Docker 并安装和部署 .NET Core 3.1
1. 安装 Docker 步骤 1.1:更新包索引并安装依赖包 先安装yum的扩展,yum-utils提供了一些额外的工具,这些工具可以执行比基本yum命令更复杂的任务 sudo yum install -y yum-utils sudo yum update -y #更新系统上已安装的所有软件包到最新…...

redis的学习(一):下载安装启动连接
简介 redis的下载,安装,启动,连接使用 nosql nosql,即非关系型数据库,和传统的关系型数据库的对比: sqlnosql数据结构结构化非结构化数据关联关联的非关联的查询方式sql查询非sql查询事务特性acidbase存…...

前端设计模式面试题汇总
面试题 1. 简述对网站重构的理解? 参考回答: 网站重构:在不改变外部行为的前提下,简化结构、添加可读性,而在网站前端保持一致的行为。也就是说是在不改变UI的情况下,对网站进行优化, 在扩展的…...
安装python3.12.2环境)
linux(CentOS、Ubuntu)安装python3.12.2环境
1.下载官网Python安装包 wget https://www.python.org/ftp/python/3.12.2/Python-3.12.2.tar.xz 1.1解压 tar -xf Python-3.12.2.tar.xz 解压完后切换到Python-3.12.2文件夹(这里根据自己解压的文件夹路径) cd /usr/packages/Python-3.12.2/ 1.2升级软件包管理器 CentOS系…...

CSS 中border-radius 属性
border-radius 属性在 CSS 中用于创建圆角边框。它可以接受一到四个值,这些值可以是长度值(如像素 px、em 等)或百分比(%)。当提供四个值时,它们分别对应于边框的左上角、右上角、右下角和左下角的圆角半径…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
