【OJ】二叉树相关OJ题
✨✨欢迎大家来到Celia的博客✨✨
🎉🎉创作不易,请点赞关注,多多支持哦🎉🎉
所属专栏:OJ题
个人主页:Celia's blog~
目录
编辑
单值二叉树
题目描述 OJ-单值二叉树
解题思路
代码实现
二叉树的最大深度
题目描述 OJ-二叉树的最大深度
解题思路
代码实现
检查两棵树是否相同
题目描述 OJ-相同的树
解题思路
代码实现
对称二叉树
题目描述 OJ-对称二叉树
解题思路
代码实现
另一颗树的子树
题目描述 OJ-另一颗树的子树
解题思路
代码实现
翻转二叉树
题目描述 OJ-翻转二叉树
解题思路
代码实现
平衡二叉树
题目描述 OJ-平衡二叉树
解题思路
代码实现
单值二叉树
-
题目描述 OJ-单值二叉树
- 如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
- 只有给定的树是单值二叉树时,才返回
true;否则返回false。
-
解题思路
本题的核心是判断左右子树的val的值是否和主干的val相等。
- 若节点为空,则返回true。
- 若不相等,返回false。
- 如果这两个条件都不满足,则递归判断左右子树。
该题调用的函数参数只有一个二叉树节点指针。为了方便起见,可以额外写一个子函数来进行递归,子函数的参数为二叉树节点指针root和该节点的值val。

(绿色数字为执行顺序)

(绿色数字执行顺序)
-
代码实现
bool _isUnivalTree(struct TreeNode* root,int val)
{if(root == NULL)return true;if(root->val != val)return false;return _isUnivalTree(root->left,val) && _isUnivalTree(root->right,val);
}
bool isUnivalTree(struct TreeNode* root)//系统调用的函数
{return _isUnivalTree(root,root->val);
}二叉树的最大深度
-
题目描述 OJ-二叉树的最大深度
- 给定一个二叉树
root,返回其最大深度。- 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
-
解题思路
本题的关键在于,该树的深度为左右子树中最大的深度。
- 如果传入的节点为空,则返回0。
- 如果节点不为空,则递归计算左右两个子树的深度,并且定义两个整型变量记录下来。
- 最后返回左右子树深度中值最大的一个。

(绿色数字执行顺序)
-
代码实现
int maxDepth(struct TreeNode* root) {if(root == NULL)return 0;int l = maxDepth(root->left);int r = maxDepth(root->right);return l > r ? l + 1 :r + 1;
}在这里要注意一定要用两个变量接收左右子树的深度,不可以将递归函数写在三目运算符中:
return maxDepth(root->left) > maxDepth(root->right) ? maxDepth(root->left) + 1 : rmaxDepth(root->right) + 1;上面的写法会导致过多的重复运算,严重拖慢了运行时间。
检查两棵树是否相同
-
题目描述 OJ-相同的树
- 给你两棵二叉树的根节点
p和q,编写一个函数来检验这两棵树是否相同。- 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
-
解题思路
- 如果传入的节点都为空,则返回true。
- 如果只有其中一个为空,另一个不为空,则返回false。
- 如果传入的节点都不为空,但是这两颗树当前节点值不同,返回false。
- 递归遍历两个左右子树,左子树和左子树比较,右子树和右子树比较,返回两个递归逻辑与的结果。
-
代码实现
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{if(p == NULL && q == NULL)return true;if(p == NULL || q == NULL)return false;if(p->val != q->val)return false;return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}对称二叉树
-
题目描述 OJ-对称二叉树
- 给你一个二叉树的根节点
root, 检查它是否轴对称。
-
解题思路
这道题和 OJ-相同的树 思路是一样的,唯一需要改变的地方为相同的树是相同方向的树进行比较,而本题是不同方向的树进行比较。
-
代码实现
bool _isSymmetric(struct TreeNode* r1,struct TreeNode* r2)
{if(r1 == NULL && r2 == NULL)return true;if(r1 == NULL || r2 == NULL)return false;if(r1->val != r2->val)return false;return _isSymmetric(r1->right,r2->left) && _isSymmetric(r1->left,r2->right);
}
bool isSymmetric(struct TreeNode* root)
{return _isSymmetric(root->left,root->right);
}另一颗树的子树
-
题目描述 OJ-另一颗树的子树
- 给你两棵二叉树
root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在,返回true;否则,返回false。- 二叉树
tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。
-
解题思路
- 本题提供的subRoot树一定为非空,那么如果传入的root节点为空,则一定不包含子树,返回false。
- 先判断subRoot树和root树的当前节点的值是否相同,若相同,检查以当前节点为根节点的树是否为subRoot树,如果是,返回true。
- 以左右子树为根节点递归左右子树,返回它们逻辑或的结果。(左右只要含有子树就符合题意)
-
代码实现
本题用到了 OJ-相同的树 的代码。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{if(p == NULL && q == NULL)return true;if(p == NULL || q == NULL)return false;if(p->val != q->val)return false;return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{if(root == NULL)return false;if(root->val == subRoot->val && isSameTree(root,subRoot))return true;return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);}翻转二叉树
-
题目描述 OJ-翻转二叉树
- 给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。
-
解题思路
- 如果传入的节点为空,返回NULL。
- 如果传入的节点非空,则交换左右子树节点的值。
- 递归调用左右子树。
- 返回根节点。
-
代码实现
struct TreeNode* invertTree(struct TreeNode* root)
{if(root == NULL)return NULL;struct TreeNode* tmp = root->right;root->right = root->left;root->left = tmp;invertTree(root->left);invertTree(root->right);return root;
}平衡二叉树
-
题目描述 OJ-平衡二叉树
- 给定一个二叉树,判断它是否是 平衡二叉树。
- 平衡二叉树 是指该树所有节点的左右子树的深度相差不超过 1。
-
解题思路
- 如果传入的节点为空,返回true。
- 定义两个变量,记录当前节点的左右子树的深度,并求出左右子树相差的绝对值。
- 若绝对值大于1,返回false。
- 递归调用左右子树,返回它们逻辑与的结果(左右两边都必须平衡)。
-
代码实现
本题用到了 OJ-二叉树的最大深度 的代码。
int TreeHeight(struct TreeNode* root)
{if(root == NULL)return 0;int r = TreeHeight(root->left);int r1 = TreeHeight(root->right);return r1 > r ? r1 + 1 : r + 1;
}
bool isBalanced(struct TreeNode* root)
{if(root == NULL)return true;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);int size = abs(leftHeight - rightHeight);//求绝对值if(size > 1)return false;return isBalanced(root->left) && isBalanced(root->right);
}相关文章:

【OJ】二叉树相关OJ题
✨✨欢迎大家来到Celia的博客✨✨ 🎉🎉创作不易,请点赞关注,多多支持哦🎉🎉 所属专栏:OJ题 个人主页:Celias blog~ 目录 编辑 单值二叉树 题目描述 OJ-单值二叉树 解题思路 …...

Blender中保存透明图片
在Blender中保存透明图片,主要是通过在渲染设置中调整背景透明度,并选择合适的文件格式来保存图像。以下是一个详细的步骤指南: 一、设置渲染属性 打开Blender并加载你想要渲染的模型。在右侧的属性编辑器中,找到并点击“渲染属…...

MySQL之索引优化
1、在进行查询时,索引列不能是表达式的一部分,也不能是函数的参数,否则无法使用索引 例如下面的查询不能使用 actor_id 列的索引: #这是错误的 SELECT actor_id FROM sakila.actor WHERE actor_id 1 5; 优化方式:…...

Spring Boot 与 Amazon S3:快速上传与下载文件的完整指南
概要 在将 Spring Boot 更新到 3 系列时,由于 javax 需要被替换为 jakarta,因此原先依赖于 javax 的 spring-cloud-starter-aws1 将无法使用(虽然在我本地环境中仍然可以正常工作)。为了确保兼容性,我将依赖关系更改为…...
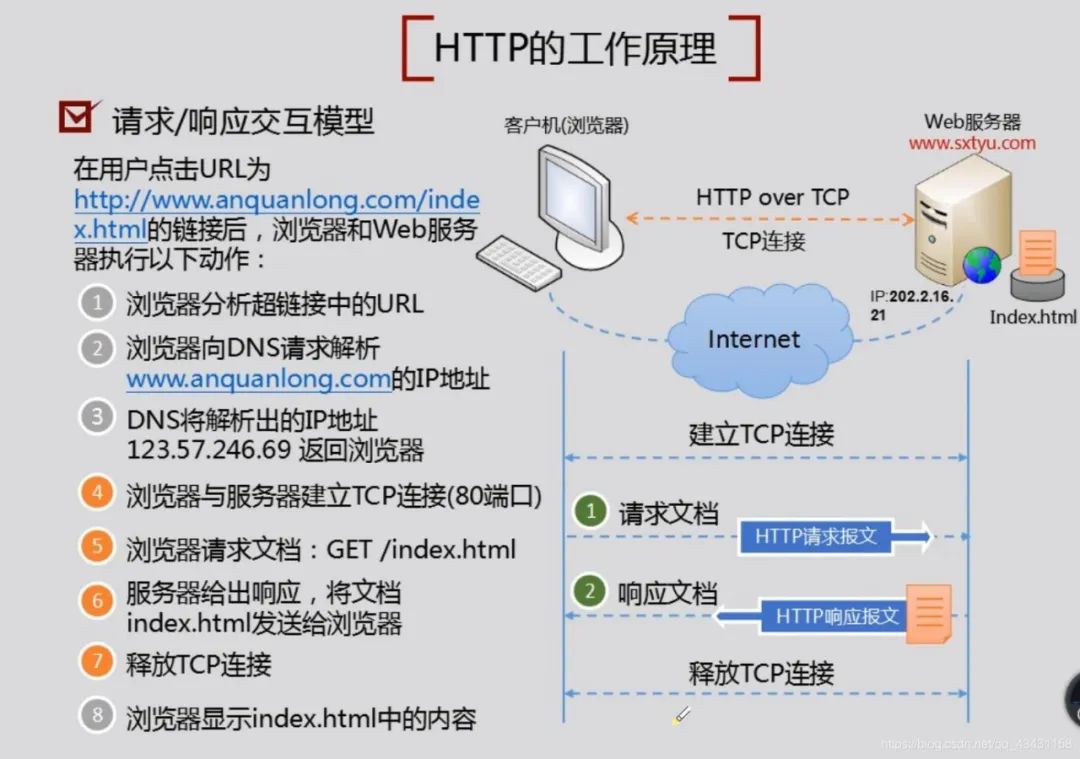
细节剖析:HTTP与HTTPS在安全性、性能等方面的不同!
HTTPS是现代互联网通信的重要基石,通过加密通信、身份验证和数据完整性保护,为数十亿用户提供了安全可靠的互联网体验。 小编整理了2GB程序员相关资料,关注微信公众号“程序员Style”回复“程序员”免费领取! 1、介绍 随着 HTT…...

MySQL面试篇章——MySQL索引
文章目录 MySQL 索引索引分类索引创建和删除索引的执行过程explain 查看执行计划explain 结果字段分析 索引的底层实现原理B-树B树哈希索引 聚集和非聚集索引MyISAM(\*.MYD,*.MYI)主键索引辅助索引(二级索引) InnoDB&a…...

WSL 2 Oracle Linux 9.1 安装配置
文章目录 环境使用体验安装 Oracle Linux 9.1修改默认存储路径默认 root 用户登录启用 systemd启用 SSH 连接WSL 无法 ping 通宿主机和域名WSL 使用主机代理(测试通过)WSL 常用命令 环境 OS:Win11 24H2 (OS 内部版本26120.1252) wsl --versio…...

MySQL日志文件详解
MySQL中的日志文件是MySQL数据库系统的重要组成部分,它们记录了数据库的运行情况、用户操作、错误信息等,对于数据库的维护、优化、故障排查和恢复都具有重要意义。以下是MySQL中几种主要日志文件的详解: 1. 二进制日志(Binary L…...
)
MySQL零散拾遗(三)
在mysql中,JOIN ON 和 WHERE 的作用和用法是怎么样的? 在MySQL中,JOIN语句用于将两个或多个表根据指定的关联条件合并成一个新的结果集。JOIN ON和WHERE子句在JOIN语句中扮演着不同的角色,它们的用法和作用如下: JOI…...

鸿蒙 使用 Refresh 实现下拉刷新
import promptAction from ohos.promptActionEntry Component struct Index {Staterefreshing: boolean falseStatelist: number[] Array(20).fill(Date.now())Buildercontent(){Stack(){Row(){LoadingProgress().height(32)Text(正在刷新...).fontSize(16).margin({left:20}…...

【JavaScript 算法】图的遍历:理解图的结构
🔥 个人主页:空白诗 文章目录 一、深度优先搜索(DFS)深度优先搜索的步骤深度优先搜索的JavaScript实现 二、广度优先搜索(BFS)广度优先搜索的步骤 三、应用场景四、总结 图的遍历是图论中的基本操作之一&am…...

Ubuntu 中默认的 root 用户密码
场景:想要切换root用户,发现得输入密码,以为是以前设置过然后一直尝试都是错误【认证失败】最后发现根本没设置过root用户,默认会随机生成root用户的密码😅 Ubuntu 中默认的 root 密码是随机的,即每次开机都…...

Rust编程-高级特性
unsafe:内存不安全 内存安全问题,例如空指针解引用 关键字unsafe来切换到不安全模式,并在被标记后的代码块中使用不安全代码 使用unsafe告诉编译器后面代码安全性自行负责 因为电脑硬件安全问题,必须编写可能不安全的代码 可以将…...
 (2024.7.22))
JavaRegexImprove练习(1) (2024.7.22)
ImproveExercise1 package RegexImprove20240722; import java.util.Scanner; public class ImproveExercise {public static void main(String[] args) {Scanner sc new Scanner(System.in);System.out.println("请输入一个字符串");String str sc.nextLine();//…...

基于YOLO模型的鸟类识别系统
鸟类识别在生物研究和保护中具有重要意义。本文将详细介绍如何使用YOLO(You Only Look Once)模型构建一个鸟类识别系统,包括UI界面、YOLOv8/v7/v6/v5代码以及训练数据集。 目录 2. 环境配置 2.1 安装Python和相关库 2.2 安装YOLO模型库 …...

WebRTC通话原理(SDP、STUN、 TURN、 信令服务器)
文章目录 1.媒体协商SDP简介 2.网络协商STUN的工作原理TURN工作原理 3.信令服务器信令服务器的主要功能信令服务器的实现方式 1.媒体协商 比如下面这个例子 A端与B端要想通信 A端视频采用VP8做解码,然后发送给B端,B端怎么解码? B端视频采用…...

面试场景题系列--(1)如果系统的 QPS 突然提升 10 倍该怎么设计?--xunznux
1. 如果系统的 QPS 突然提升 10 倍该怎么设计? 1.1 硬件的扩展微服务的拆分 如果所有的业务包括交易系统、会员信息、库存、商品等等都夹杂在一起,当流量一旦起来之后,单体架构的问题就暴露出来了,机器挂了所有的业务就全部无法…...

【数学建模】——前沿图与网络模型:新时代算法解析与应用
目录 1.图与网络的基本概念 1. 无向图和有向图 2. 简单图、完全图、赋权图 3. 顶点的度 4. 子图与图的连通性 2.图的矩阵表示 1. 关联矩阵 2. 邻接矩阵 3.最短路问题 1.Dijkstra 算法 2.Floyd 算法 4.最小生成树问题 1.Kruskal 算法 2.Prim 算法 5.着色问题 6.…...

视频分帧【截取图片】(YOLO目标检测【生成数据集】)
高效率制作数据集【按这个流程走,速度很顶】 本次制作,1059张图片【马路上流动车辆】 几乎就是全自动了,只要视频拍得好,YOLO辅助制作数据集就效率极高 视频中的图片抽取: 【由于视频内存过大,遇到报错执行…...

Redis7(二)Redis持久化双雄
持久化之RDB RDB的持久化方式是在指定时间间隔,执行数据集的时间点快照。也就是在指定的时间间隔将内存中的数据集快照写入磁盘,也就是Snapshot内存快照,它恢复时再将硬盘快照文件直接读回到内存里面。 RDB保存的是dump.rdb文件。 自动触发…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...













