【JavaScript 算法】图的遍历:理解图的结构


文章目录
- 一、深度优先搜索(DFS)
- 深度优先搜索的步骤
- 深度优先搜索的JavaScript实现
- 二、广度优先搜索(BFS)
- 广度优先搜索的步骤
- 三、应用场景
- 四、总结

图的遍历是图论中的基本操作之一,通过遍历图中的所有节点和边,可以理解图的结构并解决实际问题。常见的图遍历方法有深度优先搜索(DFS)和广度优先搜索(BFS)。本文将详细介绍这两种遍历方法的原理、实现及其应用。
一、深度优先搜索(DFS)
深度优先搜索是一种从起始节点出发,沿着图的分支尽可能深入,然后回溯并继续探索其他分支的遍历方法。
深度优先搜索的步骤
- 从起始节点开始,将其标记为已访问。
- 对于当前节点的每个相邻节点:
- 如果相邻节点未被访问,递归地执行深度优先搜索。
- 回溯到上一个节点,继续探索其他未被访问的相邻节点。

深度优先搜索的JavaScript实现
/*** 深度优先搜索算法* @param {Object} graph - 图的邻接表表示* @param {string} start - 起始节点* @param {Set} visited - 已访问节点集合*/
function depthFirstSearch(graph, start, visited = new Set()) {console.log(start); // 访问节点visited.add(start); // 将节点标记为已访问for (const neighbor of graph[start]) {if (!visited.has(neighbor)) {depthFirstSearch(graph, neighbor, visited); // 递归访问相邻节点}}
}// 示例
const graph = {A: ['B', 'C'],B: ['D', 'E'],C: ['F'],D: [],E: ['F'],F: []
};depthFirstSearch(graph, 'A'); // 输出: A B D E F C
二、广度优先搜索(BFS)
广度优先搜索是一种从起始节点开始,逐层向外扩展,直到遍历完所有节点的遍历方法。
广度优先搜索的步骤
- 从起始节点开始,将其标记为已访问,并加入队列。
- 当队列不为空时,取出队列的头节点,访问该节点的所有相邻节点。
- 对于每个相邻节点,如果未被访问过,将其标记为已访问并加入队列。
- 重复步骤2和3,直到队列为空。

/*** 广度优先搜索算法* @param {Object} graph - 图的邻接表表示* @param {string} start - 起始节点*/
function breadthFirstSearch(graph, start) {const queue = [start]; // 初始化队列,将起始节点加入队列const visited = new Set(); // 用于记录已访问的节点visited.add(start); // 将起始节点标记为已访问while (queue.length > 0) {const node = queue.shift(); // 取出队列的头节点console.log(node); // 访问节点// 访问当前节点的所有相邻节点for (const neighbor of graph[node]) {// 如果相邻节点未被访问过,将其标记为已访问并加入队列if (!visited.has(neighbor)) {visited.add(neighbor);queue.push(neighbor);}}}
}// 示例
breadthFirstSearch(graph, 'A'); // 输出: A B C D E F
三、应用场景
- 路径搜索:DFS和BFS都可以用于寻找图中的路径。
- 连通性检查:通过DFS或BFS,可以检查图的连通性,确定图中是否存在路径连接所有节点。
- 最短路径搜索:BFS适用于在无权图中寻找两个节点之间的最短路径。
- 拓扑排序:在有向无环图(DAG)中,可以使用DFS进行拓扑排序。
- 环路检测:通过DFS可以检测图中是否存在环路。
四、总结
图的遍历是理解图结构和解决图论问题的重要工具。深度优先搜索(DFS)和广度优先搜索(BFS)是两种基本的图遍历算法,它们各有特点和应用场景。通过理解和掌握这两种遍历方法,可以解决许多实际问题,如路径搜索、连通性检查、最短路径搜索、拓扑排序和环路检测等。
相关文章:

【JavaScript 算法】图的遍历:理解图的结构
🔥 个人主页:空白诗 文章目录 一、深度优先搜索(DFS)深度优先搜索的步骤深度优先搜索的JavaScript实现 二、广度优先搜索(BFS)广度优先搜索的步骤 三、应用场景四、总结 图的遍历是图论中的基本操作之一&am…...

Ubuntu 中默认的 root 用户密码
场景:想要切换root用户,发现得输入密码,以为是以前设置过然后一直尝试都是错误【认证失败】最后发现根本没设置过root用户,默认会随机生成root用户的密码😅 Ubuntu 中默认的 root 密码是随机的,即每次开机都…...

Rust编程-高级特性
unsafe:内存不安全 内存安全问题,例如空指针解引用 关键字unsafe来切换到不安全模式,并在被标记后的代码块中使用不安全代码 使用unsafe告诉编译器后面代码安全性自行负责 因为电脑硬件安全问题,必须编写可能不安全的代码 可以将…...
 (2024.7.22))
JavaRegexImprove练习(1) (2024.7.22)
ImproveExercise1 package RegexImprove20240722; import java.util.Scanner; public class ImproveExercise {public static void main(String[] args) {Scanner sc new Scanner(System.in);System.out.println("请输入一个字符串");String str sc.nextLine();//…...

基于YOLO模型的鸟类识别系统
鸟类识别在生物研究和保护中具有重要意义。本文将详细介绍如何使用YOLO(You Only Look Once)模型构建一个鸟类识别系统,包括UI界面、YOLOv8/v7/v6/v5代码以及训练数据集。 目录 2. 环境配置 2.1 安装Python和相关库 2.2 安装YOLO模型库 …...

WebRTC通话原理(SDP、STUN、 TURN、 信令服务器)
文章目录 1.媒体协商SDP简介 2.网络协商STUN的工作原理TURN工作原理 3.信令服务器信令服务器的主要功能信令服务器的实现方式 1.媒体协商 比如下面这个例子 A端与B端要想通信 A端视频采用VP8做解码,然后发送给B端,B端怎么解码? B端视频采用…...

面试场景题系列--(1)如果系统的 QPS 突然提升 10 倍该怎么设计?--xunznux
1. 如果系统的 QPS 突然提升 10 倍该怎么设计? 1.1 硬件的扩展微服务的拆分 如果所有的业务包括交易系统、会员信息、库存、商品等等都夹杂在一起,当流量一旦起来之后,单体架构的问题就暴露出来了,机器挂了所有的业务就全部无法…...

【数学建模】——前沿图与网络模型:新时代算法解析与应用
目录 1.图与网络的基本概念 1. 无向图和有向图 2. 简单图、完全图、赋权图 3. 顶点的度 4. 子图与图的连通性 2.图的矩阵表示 1. 关联矩阵 2. 邻接矩阵 3.最短路问题 1.Dijkstra 算法 2.Floyd 算法 4.最小生成树问题 1.Kruskal 算法 2.Prim 算法 5.着色问题 6.…...

视频分帧【截取图片】(YOLO目标检测【生成数据集】)
高效率制作数据集【按这个流程走,速度很顶】 本次制作,1059张图片【马路上流动车辆】 几乎就是全自动了,只要视频拍得好,YOLO辅助制作数据集就效率极高 视频中的图片抽取: 【由于视频内存过大,遇到报错执行…...

Redis7(二)Redis持久化双雄
持久化之RDB RDB的持久化方式是在指定时间间隔,执行数据集的时间点快照。也就是在指定的时间间隔将内存中的数据集快照写入磁盘,也就是Snapshot内存快照,它恢复时再将硬盘快照文件直接读回到内存里面。 RDB保存的是dump.rdb文件。 自动触发…...

发布支持TS的npm包
你现在有这么一个包,已经将他发布在npm上了,周下载量也还比较可观。美中不足的就是,这个包之前使用js写的,现在你想增加TS类型,提升用户使用体验,那么你现在可以做以下几个步骤 1.在你的包的根目录下创建一…...

计算机视觉9 全卷积网络
全卷积网络(Fully Convolutional Network,简称 FCN)在计算机视觉领域具有重要地位。 传统的卷积神经网络(CNN)在最后的输出层通常使用全连接层来进行分类任务。然而,全连接层会丢失空间信息,使得…...

02.C++入门基础(下)
1.函数重载 C支持在同一作用域中出现同名函数,但是要求这些同名函数的形参不同,可以是参数个数不同或者类型不同。这样C函数调用就表现出了多态行为,使用更灵活。C语言是不支持同一作用域中出现同名函数的。 1、参数类型不同 2、参数个数不同…...

【数据结构】探索排序的奥秘
若有不懂地方,可查阅我之前文章哦! 个人主页:小八哥向前冲~_csdn博客 所属专栏:数据结构_专栏 目录 排序的概念 几种排序方法介绍 冒泡排序 选择排序 插入排序 堆排序 向上调整建堆排序 向下调整建堆排序 希尔排序 快速…...

数据结构面试知识点总结3
#来自ウルトラマンティガ(迪迦) 1 线性表 最基本、最简单、最常用的一种数据结构。一个线性表是 n 个具有相同特性的数据元素的有限序列。 特征:数据元素之间是一对一的逻辑关系。 第一个数据元素没有前驱,称为头结点࿱…...
python-爬虫实例(5):将进酒,杯莫停!
目录 前言 将进酒,杯莫停! 一、浇给 二、前摇 1.导入selenium库 2.下载浏览器驱动 三、爬虫四步走 1.UA伪装 2.获取url 3.发送请求 4.获取响应数据进行解析并保存 总结 前言 博主身为一个农批,当然要尝试爬取王者荣耀的东西啦。 将进…...

AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理
AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理 目录 AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理 一、简单介绍 二、Transformer 1、模型架构 2、应用场景 3、Hugging …...

十大排序的稳定性和时间复杂度
十大排序算法的稳定性和时间复杂度是数据结构和算法中的重要内容。 以下是对这些算法的稳定性和时间复杂度的详细分析: 稳定性 稳定性指的是排序算法在排序过程中是否能够保持相等元素的原始相对顺序。根据这个定义,我们可以将排序算法分为稳定排序和…...
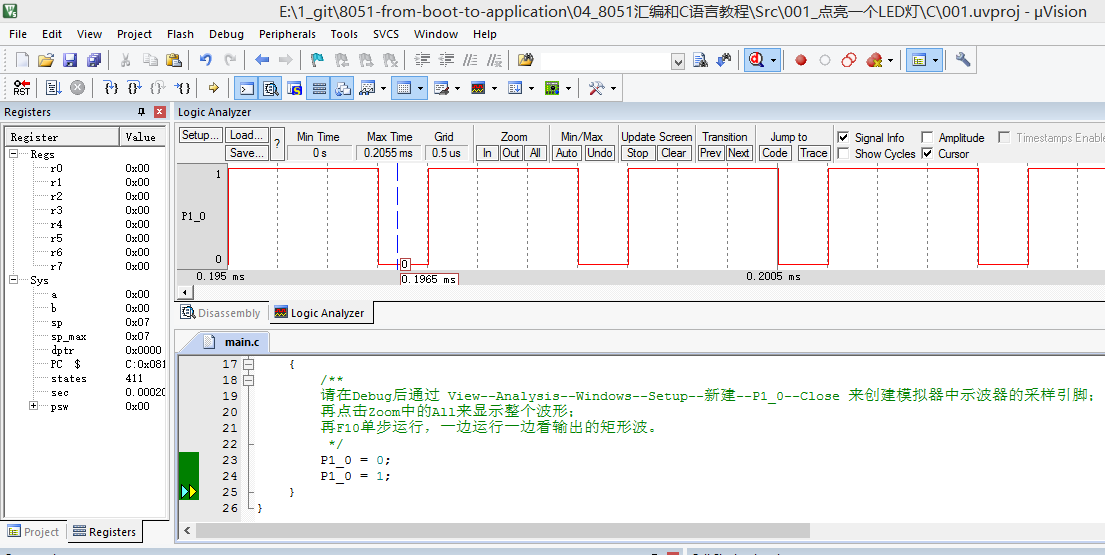
【系列教程之】1、点亮一个LED灯
1、点亮一个LED灯 作者将狼才鲸创建日期2024-07-23 CSDN教程目录地址:【目录】8051汇编与C语言系列教程本Gitee仓库原始地址:才鲸嵌入式/8051_c51_单片机从汇编到C_从Boot到应用实践教程 本源码包含C语言和汇编工程,能直接在电脑中通过Keil…...

搜维尔科技:Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作
Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作 搜维尔科技:Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
