【数据结构】探索排序的奥秘
若有不懂地方,可查阅我之前文章哦!

个人主页:小八哥向前冲~_csdn博客
所属专栏:数据结构_专栏
目录
排序的概念
几种排序方法介绍
冒泡排序
选择排序
插入排序
堆排序
向上调整建堆排序
向下调整建堆排序
希尔排序
快速排序
hoare版本快排
前后指针版本快排
非递归快排
归并排序
递归归并
非递归归并
扩展
计数排序
排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不断地在内外存之间移动数据的排序
几种排序方法介绍
注意:下面各种排序将数组升序!
冒泡排序
冒泡排序相信你们都已经非常了解了!这里我们简单介绍一下就行!
有n个数,需要升序排列。我们只需要n-1趟排序,每趟排序将最大的排到了最后一个位置!
也就是说,每趟可以选出最大一个数且在最后一个位置上!
动画演示:
时间复杂度:o(N^2)
代码:
//交换
void Swap(int* p, int* q)
{int tmp = *p;*p = *q;*q = tmp;
}//冒泡排序 o(N^2)
void BubbleSort(int* a, int n)
{for (int j = 0; j < n - 1; j++){for (int i = 0; i < n - 1 - j; i++){if (a[i] > a[i + 1]){Swap(&a[i], &a[i + 1]);}}}
}选择排序
思路:
选择排序比较简单,选择——顾名思义,不断遍历数组,选择其中最小和最大的数,将最小数放在数组左侧,最大数放在数组右侧!
对于这个排序,我不做过多解释,比较简单!但是这里有一个小坑!
图:

代码:
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int maxi = 0, mini = 0;for (int i = begin ; i <= end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[mini], &a[begin]);//begin和maxi相等时,刷新maxiif (begin == maxi){maxi = mini;}Swap(&a[maxi], &a[end]);begin++;end--;}
}插入排序
插入排序动画演示:
比如:要求升序,将一个一个数依次往前比较,比它大的往后移,知道比它小的数,再插进去!
时间复杂度:最坏情况-逆序-o(N^2) 最好情况-有序-o(N)
代码:
//插入排序
void Insert(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}
堆排序
由于前俩章介绍了堆和二叉树,这里的堆排序不过多讲述,可翻阅我之前文章!
传送门:CSDN--详解堆
我们这里介绍俩种排序方法!
向上调整建堆排序
思路:
以将数组拍成升序为例,将数组中的数建成大堆,此时第一个数就是最大的数!再将第一个数和最后一个数交换,以此循环!
代码:
//向上调整
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n&&a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[parent], &a[child]);}else{break;}}
}
//堆排序--向上调整-o(N*logN)
void HeapUpSort(int* a, int n)
{for (int i = 0; i < n; i++){AdjustUp(a, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}注意:时间复杂度——o(N*logN)
向下调整建堆排序
思路:
用向下调整的方法将数组调成大堆,那么第一个数就是数组中最大的数!然后将第一个数和数组最后一个数交换,以此循环交换!
代码:
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n&&a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[parent], &a[child]);}else{break;}}
}
//堆排序—向下调整建堆—o(N)
void HeapDownSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i > 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[end], &a[0]);AdjustDown(a, end, 0);end--;}
}希尔排序
先将数组里面的数分组,然后将分组好了的数排序,最后将整个数组利用插入排序进行最后的排序!
第一种代码:
//希尔排序 o(N^1.3)
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}
第二种代码:
//希尔排序 o(N^1.3)
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}快速排序
hoare版本快排
霍尔版本的快速排序动画演示:

思路:
先在这个数组中寻找一个参考值,将数组左边排成都比参考值小,数组右边排成都比参考值大!然后中间值将参考值交换。再将中间值左右边都这样循环往复操作,形成有序!
代码:
void Swap(int* q, int* p)
{int tmp = *q;*q = *p;*p = tmp;
}
void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = left;int begin = left, end = right;while (begin < end){//右边找小while (begin<end && a[end]>a[keyi]){end--;}//左边找大while (begin < end && a[begin] < a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}但是这样写有一点瑕疵,我们可以近一步优化!
这段代码的“瑕疵”在:
- 可能会栈溢出(递归太深)
- 可以将后面递归排序进行优化
第一个瑕疵可以:当你取的参考值是数组里面最小的,那么就只会递归后面的n-1个数!这种情况是最有可能栈溢出(递归太深)!
我们可以进行三数取中优化!
第二个瑕疵可以:当一直递归排序时,数组过大非常适合取中快排,但是当数组过小,我们没有必要用快排排序,我们可以用插入排序!
优化代码:
void Swap(int* q, int* p)
{int tmp = *q;*q = *p;*p = tmp;
}//三数取中
int GetMid(int* a, int left, int right)
{int midi = (left + right) / 2;if (a[left] < a[right]){if (a[midi] < a[left]){return left;}else if (a[midi] > a[right]){return right;}else{return midi;}}else{if (a[midi] > a[left]){return left;}else if (a[midi] < a[right]){return right;}else{return midi;}}
}
//插入排序
void Insort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}//三数取中优化int midi = GetMid(a, left, right);Swap(&a[left], &a[midi]);//小区间优化if ((right - left + 1) < 10){Insort(a+left, right - left + 1);}else{int keyi = left;int begin = left, end = right;while (begin < end){//右边找小while (begin<end && a[end]>a[keyi]){end--;}//左边找大while (begin < end && a[begin] < a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}
}前后指针版本快排
前后指针版本的快排动画演示:

思路:
俩种方法大差不差,只是相比hoare版本,前后指针更好理解。俩种都是将数组分割成俩个小数组,进行排序!用的是双指针来分割交换数组!
代码:
//三数取中
int GetMid(int* a, int left, int right)
{int midi = (left + right) / 2;if (a[left] < a[right]){if (a[midi] < a[left]){return left;}else if (a[midi] > a[right]){return right;}else{return midi;}}else{if (a[midi] > a[left]){return left;}else if (a[midi] < a[right]){return right;}else{return midi;}}
}
int Partsort02(int* a, int left, int right)
{//三数取中优化int midi = GetMid(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int prev = left;int cur = prev + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[keyi], &a[prev]);return prev;
}
void QuickSort(int* a, int left, int right)
{if (left >= right){return;}//小区间优化if ((right - left + 1) < 10){Insort(a+left, right - left + 1);}else{int keyi = Partsort02(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}
}递归固然好,但它再好也逃不过栈溢出的风险!所以我们可以将递归改成非递归!
我们可以用栈来模拟递归思想从而变成非递归!
非递归快排
我们可以将区间入栈,再将区间出栈进行排序,分成俩组,再将这俩组分别入栈(后一组先入栈),前一组出栈排序,循环往复!

代码:
注意:里面的ST为栈结构,若有不懂可去我这篇文章---栈——CSDN-小八哥向前冲
//非递归
void QuickStack(int* a, int left, int right)
{ST st;STInit(&st);STpush(&st, right);STpush(&st, left);while (!STEmpty(&st)){//出栈取数据int begin = STtop(&st);STpop(&st);int end = STtop(&st);STpop(&st);//开始排序int keyi = Partsort02(a, begin, end);//排完一趟就入栈if (keyi + 1 < end){STpush(&st, end);STpush(&st, keyi + 1);}if (begin < keyi - 1){STpush(&st, keyi - 1);STpush(&st, begin);}}
}归并排序
递归归并
倘若有这样一个数组----它的前半部分有序,后半部分也有序(只不过整体不有序),就能利用归并将这个数组排成有序!
单趟理解:

那么使用归并排序,是不是应该先要前后部分分别有序呢?我们可以将数组一直二分下去归并排!
我们可以将它一直分开,直到不能分开了,就开始归并!
理解:

整体理解:

代码:
void _MergeSort(int* a, int* tmp, int left, int right)
{if (left >= right){return;}int mid = (left + right) / 2;//分区间_MergeSort(a, tmp, left, mid);_MergeSort(a, tmp, mid + 1, right);//开始排int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int i = left;while (begin1<=end1 && begin2<=end2)//但凡有一个越界就跳出来{if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, tmp, 0, n - 1);free(tmp);tmp = NULL;
}时间复杂度:N*logN
非递归归并
非递归思路:
那么如何将递归方式改成非递归呢?一定要区别归并和快排,快排是先排序再分,归并是先分再排!快排相当于是二叉树里面的前序,而归并相当于是后序!
这里利用栈不好实现,我们可以另辟蹊径!
既然不好实现分组,那我们可以进行手动分组,然后进行归并!
理解:

代码:
void MergeSortNon(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc faild !");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//第二组完全越界了,这组就不用归并了if (begin2 >= n){break;}//第一组没越界,第二组部分越界,需要进行修正再归并if (end2 >= n){end2 = n - 1;}int j = begin1;while (begin1 <= end1 && begin2 <= end2)//但凡有一个越界就跳出来{if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));}gap *= 2;}free(tmp);tmp = NULL;
}这里解释一下为什么需要归并一部分复制一部分:
如果后部分越界了,就不会归并,那么tmp数组里面就没有没归并的数,只有归并了的数,如果是全部归并了再去复制一份的话,就直接覆盖了原来就有的数值!所以归并一部分再复制一部分是再好不过的选择!
扩展
计数排序
计数排序和其他排序方法截然不同,它摒弃了以往的比较大小的方法,转化成计数的方法!
我们上图比较好理解:

代码:
void CountSort(int* a, int n)
{int max = a[0], min = a[0];for (int i = 0; i < n; i++){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int range = max - min + 1;int* count = (int*)calloc(range,sizeof(int));if (count == NULL){perror("malloc faild!");return;}//开始计数for (int i = 0; i < n; i++){count[a[i] - min]++;}//开始往回写int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}free(count);count = NULL;
}这里代码有个小细节:
开辟空间不用malloc,而用calloc,是因为我们新开辟的数组里面元素都要置0,再进行计数,而calloc开辟完了空间就会将数组元素全部置0!
全部排序总结

好了,今天的分享就到这里,我们在C++不见不散!
相关文章:

【数据结构】探索排序的奥秘
若有不懂地方,可查阅我之前文章哦! 个人主页:小八哥向前冲~_csdn博客 所属专栏:数据结构_专栏 目录 排序的概念 几种排序方法介绍 冒泡排序 选择排序 插入排序 堆排序 向上调整建堆排序 向下调整建堆排序 希尔排序 快速…...

数据结构面试知识点总结3
#来自ウルトラマンティガ(迪迦) 1 线性表 最基本、最简单、最常用的一种数据结构。一个线性表是 n 个具有相同特性的数据元素的有限序列。 特征:数据元素之间是一对一的逻辑关系。 第一个数据元素没有前驱,称为头结点࿱…...
python-爬虫实例(5):将进酒,杯莫停!
目录 前言 将进酒,杯莫停! 一、浇给 二、前摇 1.导入selenium库 2.下载浏览器驱动 三、爬虫四步走 1.UA伪装 2.获取url 3.发送请求 4.获取响应数据进行解析并保存 总结 前言 博主身为一个农批,当然要尝试爬取王者荣耀的东西啦。 将进…...

AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理
AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理 目录 AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理 一、简单介绍 二、Transformer 1、模型架构 2、应用场景 3、Hugging …...

十大排序的稳定性和时间复杂度
十大排序算法的稳定性和时间复杂度是数据结构和算法中的重要内容。 以下是对这些算法的稳定性和时间复杂度的详细分析: 稳定性 稳定性指的是排序算法在排序过程中是否能够保持相等元素的原始相对顺序。根据这个定义,我们可以将排序算法分为稳定排序和…...
【系列教程之】1、点亮一个LED灯
1、点亮一个LED灯 作者将狼才鲸创建日期2024-07-23 CSDN教程目录地址:【目录】8051汇编与C语言系列教程本Gitee仓库原始地址:才鲸嵌入式/8051_c51_单片机从汇编到C_从Boot到应用实践教程 本源码包含C语言和汇编工程,能直接在电脑中通过Keil…...

搜维尔科技:Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作
Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作 搜维尔科技:Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作...

机器学习 | 阿里云安全恶意程序检测
目录 一、数据探索1.1 数据说明1.2 训练集数据探索1.2.1 数据特征类型1.2.2 数据分布1.2.3 缺失值1.2.4 异常值1.2.5 标签分布探索 1.3 测试集探索1.3.1 数据信息1.3.2 缺失值1.3.3 数据分布1.3.4 异常值 1.4 数据集联合分析1.4.1 file_id 分析1.4.2 API 分析 二、特征工程与基…...

python打包exe文件-实现记录
1、使用pyinstaller库 安装库: pip install pyinstaller打包命令标注主入库程序: pyinstaller -F.\程序入口文件.py 出现了一个问题就是我在打包运行之后会出现有一些插件没有被打包。 解决问题: 通过添加--hidden-importcomtypes.strea…...

基本的DQL语句-单表查询
一、DQL语言 DQL(Data Query Language 数据查询语言)。用途是查询数据库数据,如SELECT语句。是SQL语句 中最核心、最重要的语句,也是使用频率最高的语句。其中,可以根据表的结构和关系分为单表查询和多 表联查。 注意:所有的查询…...

Vue3 对比 Vue2
相关信息简介2020年9月18日,Vue.js发布3.0版本,代号:One Piece(海贼王) 2 年多开发, 100位贡献者, 2600次提交, 600次 PR、30个RFC Vue3 支持 vue2 的大多数特性 可以更好的支持 Typescript,提供了完整的…...

2024中国大学生算法设计超级联赛(1)
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,彩笔ACMer一枚。 🏀所属专栏:杭电多校集训 本文用于记录回顾总结解题思路便于加深理解。 📢📢📢传送门 A - 循环位移解…...

offer题目51:数组中的逆序对
题目描述:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。例如,在数组{7,5,6,4}中,一共存在5个逆序对,分别是(7…...

45、PHP 实现滑动窗口的最大值
题目: PHP 实现滑动窗口的最大值 描述: 给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。 例如: 如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3, 那么一共存在6个滑动窗口, 他们的最大值…...

【计算机视觉】siamfc论文复现实现目标追踪
什么是目标跟踪 使用视频序列第一帧的图像(包括bounding box的位置),来找出目标出现在后序帧位置的一种方法。 什么是孪生网络结构 孪生网络结构其思想是将一个训练样本(已知类别)和一个测试样本(未知类别)输入到两个CNN(这两个CNN往往是权值共享的)中࿰…...

数学建模学习(111):改进遗传算法(引入模拟退火、轮盘赌和网格搜索)求解JSP问题
文章目录 一、车间调度问题1.1目前处理方法1.2简单案例 二、基于改进遗传算法求解车间调度2.1车间调度背景介绍2.2遗传算法介绍2.2.1基本流程2.2.2遗传算法的基本操作和公式2.2.3遗传算法的优势2.2.4遗传算法的不足 2.3讲解本文思路及代码2.4算法执行结果: 三、本文…...

Golang | Leetcode Golang题解之第241题为运算表达式设计优先级
题目: 题解: const addition, subtraction, multiplication -1, -2, -3func diffWaysToCompute(expression string) []int {ops : []int{}for i, n : 0, len(expression); i < n; {if unicode.IsDigit(rune(expression[i])) {x : 0for ; i < n &…...

Unity客户端接入原生Google支付
Unity客户端接入原生Google支付 1. Google后台配置2. 开始接入Java部分C#部分Lua部分 3. 导出工程打包测试参考踩坑注意 1. Google后台配置 找到内部测试(这个测试轨道过审最快),打包上传,这个包不需要接入支付,如果已…...

Spring Cloud之五大组件
Spring Cloud 是一系列框架的有序集合,为开发者提供了快速构建分布式系统的工具。这些组件可以帮助开发者做服务发现,配置管理,负载均衡,断路器,智能路由,微代理,控制总线等。以下是 Spring Cl…...
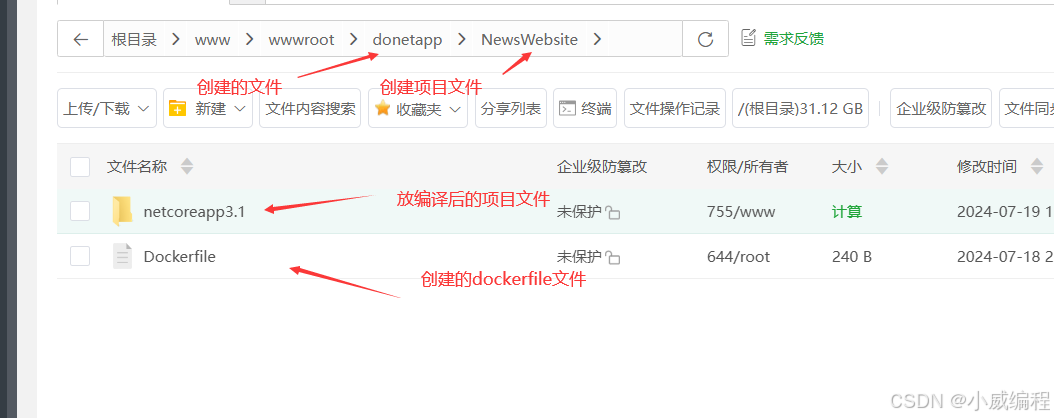
在 CentOS 7 上安装 Docker 并安装和部署 .NET Core 3.1
1. 安装 Docker 步骤 1.1:更新包索引并安装依赖包 先安装yum的扩展,yum-utils提供了一些额外的工具,这些工具可以执行比基本yum命令更复杂的任务 sudo yum install -y yum-utils sudo yum update -y #更新系统上已安装的所有软件包到最新…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
