《SeTformer Is What You Need for Vision and Language》
会议:AAAI
年份:2024
论文:DDAE: Towards Deep Dynamic Vision BERT Pretraining - AMiner![]() https://www.aminer.cn/pub/6602613613fb2c6cf6c387c2/ddae-towards-deep-dynamic-vision-bert-pretraining
https://www.aminer.cn/pub/6602613613fb2c6cf6c387c2/ddae-towards-deep-dynamic-vision-bert-pretraining
摘要
这篇论文介绍了一种新型的变换器模型,名为SeTformer,它针对视觉和语言任务进行了优化。SeTformer的核心创新是将传统的点积自注意力(DPSA)替换为一种基于自我最优传输(Self-optimal Transport,简称SeT)的机制。这种替换旨在解决传统变换器在处理长序列时面临的计算效率低下的问题,同时保持或提升性能。SeT基于两个关键的softmax属性:维持非负的注意力矩阵和使用非线性重加权机制来强调输入序列中的重要token。通过引入核成本函数来实现最优传输,SeTformer有效地满足了这些属性。实验结果表明,SeTformer在多个任务上都取得了令人印象深刻的性能,包括在ImageNet-1K上的分类准确率、目标检测和语义分割等。
拟解决的问题
传统变换器(如Vision Transformer, ViT)在处理长序列数据时,由于softmax操作导致的二次时间和内存复杂度,使得模型训练和推理变得非常昂贵。这限制了变换器在处理长文档或高分辨率图像等任务时的应用。
创新之处
- 自我最优传输(SeT):提出了一种新的自注意力机制,使用最优传输(OT)和核方法来计算输入特征之间的对齐分数,代替了传统的点积操作。
- 核特征映射:通过将输入特征映射到再生核希尔伯特空间(RKHS),保持了注意力矩阵的非负性质。
- 效率与性能的平衡:在减少参数和计算量的同时,SeTformer在多个视觉和语言任务上取得了与现有最先进方法相媲美或更好的结果。
方法

传统的自注意力方法:输入序列的每个元素(token)都会计算与其他所有元素的关系,通常使用点积(Dot Product)来衡量元素间的相似度。然后,通过softmax函数对这些相似度进行归一化,得到注意力权重,这些权重用于加权求和,形成每个元素的输出表示。

尽管自注意力在捕捉序列内长距离依赖方面非常有效,但其计算复杂度随着序列长度的增加而呈二次方增长,这在处理长序列时(如高分辨率图像或长文本)变得非常昂贵。
为了解决以上问题,提出了自我最优传输(SeT),这是一种新颖的自注意力替代方案。SeT利用最优传输(OT)理论来计算输入特征之间的对齐分数,而不是传统的点积操作。
SeT的关键步骤:
- 特征映射到RKHS:将输入特征向量映射到再生核希尔伯特空间(RKHS),使用正定核函数保证映射后的向量是非负的。
- OT对齐:使用最优传输(OT)来对齐输入特征和参考特征。OT通过计算最小成本的传输计划,来找到输入特征与参考特征之间的最佳匹配。
- 加权聚合:通过OT得到的对齐分数作为权重,对输入特征进行加权聚合,形成输出特征。
特征映射到RKHS
-
选择或定义核函数:首先,选择一个合适的正定核函数 𝐾(𝑥,𝑥′),它能够将原始空间 𝑋 中的数据点映射到一个高维特征空间 𝐹。常用的核函数包括高斯核、多项式核、拉普拉斯核等。
-
特征映射:通过核函数定义一个特征映射 𝑢:𝑋→𝐹,其中 𝐹 是一个希尔伯特空间。在RKHS中,任意两个点 𝑥 和 𝑥′ 之间的核函数值 𝐾(𝑥,𝑥′) 可以表示为这两个点在 𝐹 空间中映射的内积,即 𝐾(𝑥,𝑥′)=〈𝑢(𝑥),𝑢(𝑥′)〉𝐹。
由于核函数是正定的,它保证了映射后的向量之间的内积是非负的,这与softmax操作的非负性相一致。
OT对齐
OT是数学中的一个概念,它描述了将一个概率分布转换为另一个概率分布的最优方式,这可以类比为将一堆“土”(代表概率质量)从一个位置移动到另一个位置,最小化运输成本。
用于在特征空间中对齐输入和参考特征。在SeTformer中,OT对齐用于计算输入特征与一组参考特征之间的相似性或对齐分数,这些分数随后用于加权聚合,形成注意力机制的输出。
OT对齐的关键步骤:
1. 用Kantorovich形式表示,通过最小化成本函数加上熵正则化项来求解:

C 是成本矩阵,𝑇 是传输计划矩阵,𝜇 和 𝜈 是分别与 𝑋 和 𝑌 相关的分布,𝜖 是正则化参数,𝐻(𝑇) 是传输计划的熵,计算公式如下:
![]()
2. 使用Sinkhorn算法来求解上述优化问题,该算法通过迭代过程不断调整传输计划 𝑇 以逼近最优解。OT 根据各个元素/标记在输入中的重要性为不同的元素/标记分配不同的权重,类似于 softmax 注意力中的重新加权方案。换句话说,T(x, x′) 中的每个值表示 x 与 x′ 的元素对齐的权重或重要性。
Self-optimal Transport (SeT)
- 将输入输入特征 𝑋 和参考特征 𝑌 映射到RKHS,这些参考特征用于与输入特征进行对齐
- 使用OT来计算输入特征 𝑋 和参考特征 𝑌 之间的对齐分数,通过最小化传输成本来找到最优的传输计划 𝑇。
- 根据OT得到的传输计划 𝑇,进而形成对齐矩阵 𝐴:
,其中U是输入特征在RKHS中的表示
- 将输入特征 𝑥 通过传输计划 𝐴 与参考特征 𝑦 的加权聚合
![]()
输入特征:通过相关网络提取的图像特征
参考特征:参考特征是一组预先计算好的向量,它们代表了输入数据中的关键特征或模式。可以通过聚类算法(如K-means)从训练数据中生成的。这种方法可以捕捉到数据中的代表性特征,并将它们用作参考特征集。参考特征在模型中起到了锚点的作用,帮助模型通过OT对齐来聚合输入特征。
总的来说,在SeTformer中,SeT用于替代传统的自注意力机制,通过以下步骤:
- 输入特征通过卷积层进行下采样和嵌入。
- 使用SeT计算输入特征与参考特征之间的对齐分数。
- 根据对齐分数进行特征的加权聚合,生成新的表示。
- 这些表示被送入后续的网络层,如多层感知机(MLP)和归一化层。
结论
SeTformer展示了在视觉和语言任务中的高效性和有效性。通过一系列实验验证了其在图像分类、目标检测和语义分割等任务上的优越性能。此外,SeTformer在语言建模任务上也取得了良好的结果,证明了其在不同领域的泛化能力。论文指出,SeTformer为探索更好的基于内容的交互提供了新的视角,有助于提升视觉识别模型的性能。
相关文章:

《SeTformer Is What You Need for Vision and Language》
会议:AAAI 年份:2024 论文:DDAE: Towards Deep Dynamic Vision BERT Pretraining - AMinerhttps://www.aminer.cn/pub/6602613613fb2c6cf6c387c2/ddae-towards-deep-dynamic-vision-bert-pretraining 摘要 这篇论文介绍了一种新型的变换器…...

[保姆级教程]uniapp安装使用uViewUI教程
文章目录 创建 UniApp 项目下载uView UI下载安装方式步骤 1: 安装 uView UI步骤 2: 查看uView UI是否下载成功步骤 3: 引入 uView 主 JS 库步骤 4: 引入 uView 的全局 SCSS 主题文件步骤 5: 引入 uView 基础样式步骤 6: 配置 easycom 组件模式注意事项 NPM方式步骤 1: 安装 uVi…...

网络安全法规对企业做等保有哪些具体规定?
网络安全法规对企业做等保的具体规定 根据《中华人民共和国网络安全法》,企业作为网络运营者,需要履行网络安全等级保护制度的相关义务,确保网络安全和数据保护。具体规定包括: 网络安全等级保护制度:企业应根据网络安…...

Java开发中超好用Orika属性映射工具
Orika属性映射工具 引入pom依赖 <dependency><groupId>ma.glasnost.orika</groupId><artifactId>orika-core</artifactId><version>1.5.4</version></dependency>上干货 封装的工具类:OriUtilsimport ma.glasnost.orika.Map…...

qt初入门8:下拉框,输入框模糊查询,提示简单了解 (借助QCompleter)
实现一个简单的模糊查询的逻辑,输入框能提示相关项。 主要借助qt的QCompleter 类( Qt 框架中提供的一个用于自动补全和模糊搜索的类),结合一些控件,比如QComboBox和QLineEdit,实现模糊查询的功能。 1&…...

【qt】VS中如何配置Qt环境
https://download.qt.io/official_releases/vsaddin/ 首先需要下载一下vsaddin,上面的是下载的网站. 下载的时候可能会出现下图的情况 说明你下的vsaddin和您的VS版本不匹配,所以你可以多下几个其他版本的vsAddin,一般都是和你VS版本相匹配的才可以,如Vs2022,那就试试vsaddin2…...

对于相同网段的IP,部分无法ping通问题
现象1:在Linux上执行 ping 192.168.1.232,无法ping通 分析1:使用ifconfig查询,联网使用eth0口,只能上网192.168.10.xx网段,需要增加网段 解决方法:使用ip addr 查询,本身只具备10网…...
Unity发布XR中用于worldbuilding的全新电子书
通过身临其境的虚拟领域开始旅程,在维度之间传送,或将数字奇迹与现实世界融合——虚拟现实(VR)和混合现实(MR)的千万种可能性将邀请创作者把他们的想象力带入生活。 Unity发布的最新版综合指南将帮助有抱负的创作者和经验丰富的开发者深入研究和理解构建…...

Vue3相比于Vue2进行了哪些更新
1、响应式原理 vue2 vue2中采用 defineProperty 来劫持整个对象,然后进行深度遍历所有属性,给每个属性添加getter和setter,结合发布订阅模式实现响应式。 存在的问题: 检测不到对象属性的添加和删除数组API方法无法监听到需要对…...

Unity UGUI 之 Slider
本文仅作学习笔记与交流,不作任何商业用途 本文包括但不限于unity官方手册,唐老狮,麦扣教程知识,引用会标记,如有不足还请斧正 1.Slider是什么 滑块,由三部分组成:背景 填充条 手柄 填充条就是…...

这7款高效爬虫工具软件,非常实用!
在当今数据驱动的时代,自动化爬虫工具和软件成为了许多企业和个人获取数据的重要手段。这里会介绍6款功能强大、操作简便的自动化爬虫工具,用好了可以更高效地进行数据采集。 1. 八爪鱼采集器 八爪鱼是一款功能强大的桌面端爬虫软件,主打可…...

【OJ】二叉树相关OJ题
✨✨欢迎大家来到Celia的博客✨✨ 🎉🎉创作不易,请点赞关注,多多支持哦🎉🎉 所属专栏:OJ题 个人主页:Celias blog~ 目录 编辑 单值二叉树 题目描述 OJ-单值二叉树 解题思路 …...

Blender中保存透明图片
在Blender中保存透明图片,主要是通过在渲染设置中调整背景透明度,并选择合适的文件格式来保存图像。以下是一个详细的步骤指南: 一、设置渲染属性 打开Blender并加载你想要渲染的模型。在右侧的属性编辑器中,找到并点击“渲染属…...

MySQL之索引优化
1、在进行查询时,索引列不能是表达式的一部分,也不能是函数的参数,否则无法使用索引 例如下面的查询不能使用 actor_id 列的索引: #这是错误的 SELECT actor_id FROM sakila.actor WHERE actor_id 1 5; 优化方式:…...

Spring Boot 与 Amazon S3:快速上传与下载文件的完整指南
概要 在将 Spring Boot 更新到 3 系列时,由于 javax 需要被替换为 jakarta,因此原先依赖于 javax 的 spring-cloud-starter-aws1 将无法使用(虽然在我本地环境中仍然可以正常工作)。为了确保兼容性,我将依赖关系更改为…...
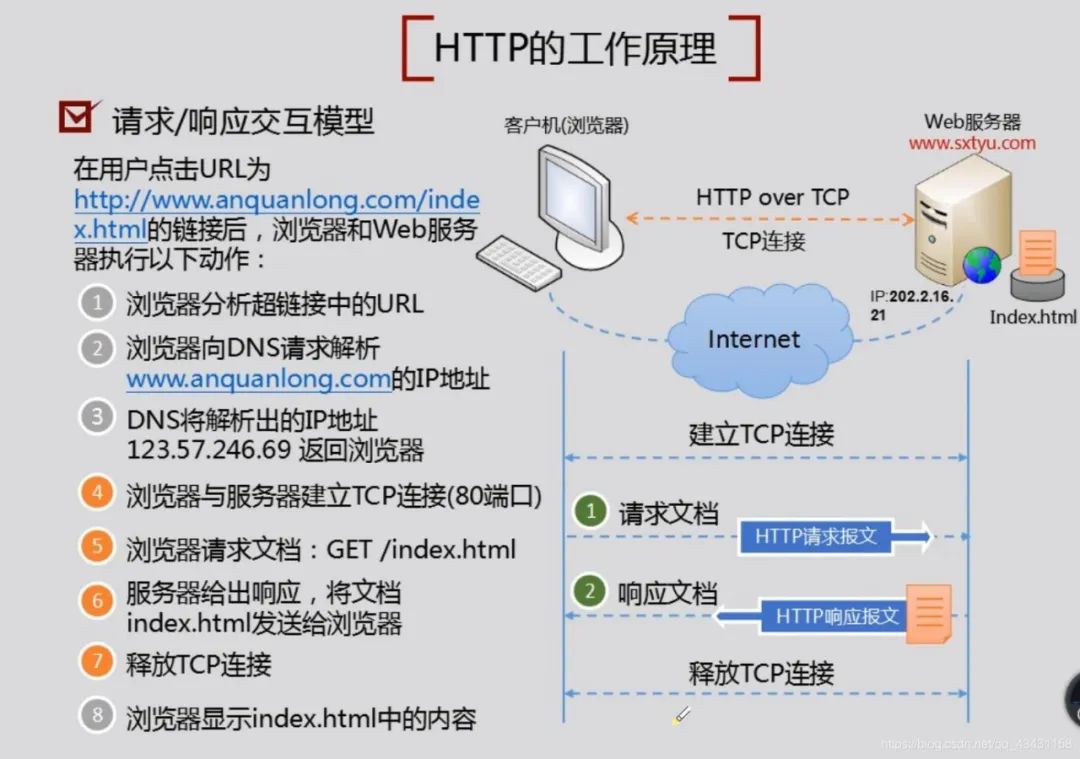
细节剖析:HTTP与HTTPS在安全性、性能等方面的不同!
HTTPS是现代互联网通信的重要基石,通过加密通信、身份验证和数据完整性保护,为数十亿用户提供了安全可靠的互联网体验。 小编整理了2GB程序员相关资料,关注微信公众号“程序员Style”回复“程序员”免费领取! 1、介绍 随着 HTT…...

MySQL面试篇章——MySQL索引
文章目录 MySQL 索引索引分类索引创建和删除索引的执行过程explain 查看执行计划explain 结果字段分析 索引的底层实现原理B-树B树哈希索引 聚集和非聚集索引MyISAM(\*.MYD,*.MYI)主键索引辅助索引(二级索引) InnoDB&a…...

WSL 2 Oracle Linux 9.1 安装配置
文章目录 环境使用体验安装 Oracle Linux 9.1修改默认存储路径默认 root 用户登录启用 systemd启用 SSH 连接WSL 无法 ping 通宿主机和域名WSL 使用主机代理(测试通过)WSL 常用命令 环境 OS:Win11 24H2 (OS 内部版本26120.1252) wsl --versio…...

MySQL日志文件详解
MySQL中的日志文件是MySQL数据库系统的重要组成部分,它们记录了数据库的运行情况、用户操作、错误信息等,对于数据库的维护、优化、故障排查和恢复都具有重要意义。以下是MySQL中几种主要日志文件的详解: 1. 二进制日志(Binary L…...
)
MySQL零散拾遗(三)
在mysql中,JOIN ON 和 WHERE 的作用和用法是怎么样的? 在MySQL中,JOIN语句用于将两个或多个表根据指定的关联条件合并成一个新的结果集。JOIN ON和WHERE子句在JOIN语句中扮演着不同的角色,它们的用法和作用如下: JOI…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
