vscode调试nextjs前端后端程序、nextjs api接口
最近有一个项目使用了nextjs框架,并且使用nextjs同时实现了前后端,由于之前前后端都是分离的,前端的调试可以通过在代码种添加debugger或者直接在浏览器中打断点实现,现在想调试后端接口,前面的方式就不适用了。故研究了如何适用vscode在本地调试。
参考文档:vscode
1.打开vscode,打开要调试的项目,点击侧边运行和调试按钮,我这是中文版,英文版对应running and debugging

2.如果之前没有配置过,将出现下面的页面,点击“创建launch.json文件”
如果已经有launch.json文件可以,跳过这一步,直接打开.vscode目录下的launch.json
3.在launch.json的configurations中添加配置:
{"name": "Next.js: debug server-side","type": "node-terminal","request": "launch","command": "pnpm run dev",//根据自己项目的运行命令调整"cwd": "${workspaceFolder}/projects/app" //如果执行commond的目录就是当前项目的根目录则无需此配置,否则配置为将运行项目根目录${workspaceFolder}代表当前工作目录},
由于是调试nextjs,这块的配置可以参考官方给出的配置
我的整个配置文件如下:
{"version": "0.2.0","configurations": [{"name": "Next.js: debug server-side","type": "node-terminal","request": "launch","command": "pnpm run dev","cwd": "${workspaceFolder}/projects/app"},{"name": "Next.js: debug client-side","type": "chrome","request": "launch","url": "http://localhost:3000"},{"name": "Next.js: debug full stack","type": "node-terminal","request": "launch","command": "npm run dev","serverReadyAction": {"pattern": "- Local:.+(https?://.+)","uriFormat": "%s","action": "debugWithChrome"}}]
}
4.保存launch.json后,重新点击侧边“运行与调试”按钮
现在面板就会变成这样:

5.点击下拉框选择自己要调试的配置名称

6.选择要调试的程序后,点击旁边的绿色小三角,运行项目

7.项目启动后,在项目中任意想调试的地方的代码序号前面点击添加断点,方法如下图:

8.可以在侧边查看所有断点

9.当有代码进入断点处,在侧边将显示当前各变量值,在上方可以通过断点相关操作继续、逐过程执行后续流程

10.以上就是调试过程,结束调试点击结束按钮即可

相关文章:

vscode调试nextjs前端后端程序、nextjs api接口
最近有一个项目使用了nextjs框架,并且使用nextjs同时实现了前后端,由于之前前后端都是分离的,前端的调试可以通过在代码种添加debugger或者直接在浏览器中打断点实现,现在想调试后端接口,前面的方式就不适用了。故研究…...

《SeTformer Is What You Need for Vision and Language》
会议:AAAI 年份:2024 论文:DDAE: Towards Deep Dynamic Vision BERT Pretraining - AMinerhttps://www.aminer.cn/pub/6602613613fb2c6cf6c387c2/ddae-towards-deep-dynamic-vision-bert-pretraining 摘要 这篇论文介绍了一种新型的变换器…...

[保姆级教程]uniapp安装使用uViewUI教程
文章目录 创建 UniApp 项目下载uView UI下载安装方式步骤 1: 安装 uView UI步骤 2: 查看uView UI是否下载成功步骤 3: 引入 uView 主 JS 库步骤 4: 引入 uView 的全局 SCSS 主题文件步骤 5: 引入 uView 基础样式步骤 6: 配置 easycom 组件模式注意事项 NPM方式步骤 1: 安装 uVi…...

网络安全法规对企业做等保有哪些具体规定?
网络安全法规对企业做等保的具体规定 根据《中华人民共和国网络安全法》,企业作为网络运营者,需要履行网络安全等级保护制度的相关义务,确保网络安全和数据保护。具体规定包括: 网络安全等级保护制度:企业应根据网络安…...

Java开发中超好用Orika属性映射工具
Orika属性映射工具 引入pom依赖 <dependency><groupId>ma.glasnost.orika</groupId><artifactId>orika-core</artifactId><version>1.5.4</version></dependency>上干货 封装的工具类:OriUtilsimport ma.glasnost.orika.Map…...

qt初入门8:下拉框,输入框模糊查询,提示简单了解 (借助QCompleter)
实现一个简单的模糊查询的逻辑,输入框能提示相关项。 主要借助qt的QCompleter 类( Qt 框架中提供的一个用于自动补全和模糊搜索的类),结合一些控件,比如QComboBox和QLineEdit,实现模糊查询的功能。 1&…...

【qt】VS中如何配置Qt环境
https://download.qt.io/official_releases/vsaddin/ 首先需要下载一下vsaddin,上面的是下载的网站. 下载的时候可能会出现下图的情况 说明你下的vsaddin和您的VS版本不匹配,所以你可以多下几个其他版本的vsAddin,一般都是和你VS版本相匹配的才可以,如Vs2022,那就试试vsaddin2…...

对于相同网段的IP,部分无法ping通问题
现象1:在Linux上执行 ping 192.168.1.232,无法ping通 分析1:使用ifconfig查询,联网使用eth0口,只能上网192.168.10.xx网段,需要增加网段 解决方法:使用ip addr 查询,本身只具备10网…...
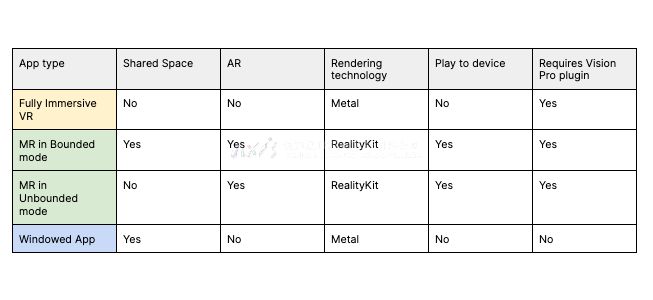
Unity发布XR中用于worldbuilding的全新电子书
通过身临其境的虚拟领域开始旅程,在维度之间传送,或将数字奇迹与现实世界融合——虚拟现实(VR)和混合现实(MR)的千万种可能性将邀请创作者把他们的想象力带入生活。 Unity发布的最新版综合指南将帮助有抱负的创作者和经验丰富的开发者深入研究和理解构建…...

Vue3相比于Vue2进行了哪些更新
1、响应式原理 vue2 vue2中采用 defineProperty 来劫持整个对象,然后进行深度遍历所有属性,给每个属性添加getter和setter,结合发布订阅模式实现响应式。 存在的问题: 检测不到对象属性的添加和删除数组API方法无法监听到需要对…...

Unity UGUI 之 Slider
本文仅作学习笔记与交流,不作任何商业用途 本文包括但不限于unity官方手册,唐老狮,麦扣教程知识,引用会标记,如有不足还请斧正 1.Slider是什么 滑块,由三部分组成:背景 填充条 手柄 填充条就是…...

这7款高效爬虫工具软件,非常实用!
在当今数据驱动的时代,自动化爬虫工具和软件成为了许多企业和个人获取数据的重要手段。这里会介绍6款功能强大、操作简便的自动化爬虫工具,用好了可以更高效地进行数据采集。 1. 八爪鱼采集器 八爪鱼是一款功能强大的桌面端爬虫软件,主打可…...

【OJ】二叉树相关OJ题
✨✨欢迎大家来到Celia的博客✨✨ 🎉🎉创作不易,请点赞关注,多多支持哦🎉🎉 所属专栏:OJ题 个人主页:Celias blog~ 目录 编辑 单值二叉树 题目描述 OJ-单值二叉树 解题思路 …...

Blender中保存透明图片
在Blender中保存透明图片,主要是通过在渲染设置中调整背景透明度,并选择合适的文件格式来保存图像。以下是一个详细的步骤指南: 一、设置渲染属性 打开Blender并加载你想要渲染的模型。在右侧的属性编辑器中,找到并点击“渲染属…...

MySQL之索引优化
1、在进行查询时,索引列不能是表达式的一部分,也不能是函数的参数,否则无法使用索引 例如下面的查询不能使用 actor_id 列的索引: #这是错误的 SELECT actor_id FROM sakila.actor WHERE actor_id 1 5; 优化方式:…...

Spring Boot 与 Amazon S3:快速上传与下载文件的完整指南
概要 在将 Spring Boot 更新到 3 系列时,由于 javax 需要被替换为 jakarta,因此原先依赖于 javax 的 spring-cloud-starter-aws1 将无法使用(虽然在我本地环境中仍然可以正常工作)。为了确保兼容性,我将依赖关系更改为…...
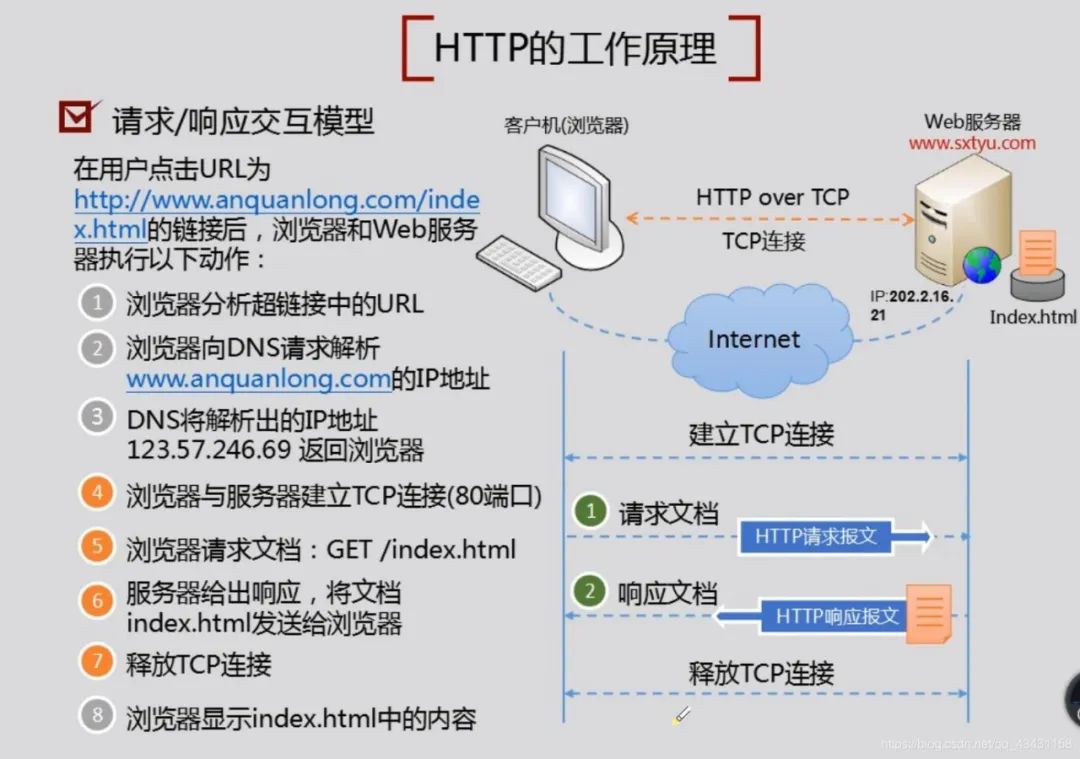
细节剖析:HTTP与HTTPS在安全性、性能等方面的不同!
HTTPS是现代互联网通信的重要基石,通过加密通信、身份验证和数据完整性保护,为数十亿用户提供了安全可靠的互联网体验。 小编整理了2GB程序员相关资料,关注微信公众号“程序员Style”回复“程序员”免费领取! 1、介绍 随着 HTT…...

MySQL面试篇章——MySQL索引
文章目录 MySQL 索引索引分类索引创建和删除索引的执行过程explain 查看执行计划explain 结果字段分析 索引的底层实现原理B-树B树哈希索引 聚集和非聚集索引MyISAM(\*.MYD,*.MYI)主键索引辅助索引(二级索引) InnoDB&a…...

WSL 2 Oracle Linux 9.1 安装配置
文章目录 环境使用体验安装 Oracle Linux 9.1修改默认存储路径默认 root 用户登录启用 systemd启用 SSH 连接WSL 无法 ping 通宿主机和域名WSL 使用主机代理(测试通过)WSL 常用命令 环境 OS:Win11 24H2 (OS 内部版本26120.1252) wsl --versio…...

MySQL日志文件详解
MySQL中的日志文件是MySQL数据库系统的重要组成部分,它们记录了数据库的运行情况、用户操作、错误信息等,对于数据库的维护、优化、故障排查和恢复都具有重要意义。以下是MySQL中几种主要日志文件的详解: 1. 二进制日志(Binary L…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
