7.23模拟赛总结 [数据结构优化dp] + [神奇建图]
目录
- 复盘
- 题解
- T2
- T4
复盘
浅复盘下吧…
7:40 开题
看 T1 ,起初以为和以前某道题有点像,子序列划分,注意到状态数很少,搜出来所有状态然后 dp,然后发现这个 T1 和那个毛关系没有
浏览了一下,感觉 T2 题面又臭又长,意思也很恶心;T3 树上 ds 看上去很亲切;T4 一眼就不太可做
回来看 T1,发现很 sb,每次肯定贪心选最优的后缀,至于选 m 的限制,填满一段后再贪心往前选就行
8:04 码完了,小样例顺利过掉,一测大样例发现小数点后面不对,想了想应该不会是精度问题,可能做法假了
然后 不断证明结论+修改一些毫无影响的细节,仍然和大样例不上,最后决定把题面重读一遍,知道看到了 “相对误差”,6,突然想到我学过高中物理。。。到 8:50 才交上去
快开 T2,朴素的想法当然是 二维状态记 Max,但这个显然不太有优化空间(这种状态设计只有 i − 1 i-1 i−1 到 i i i 只有 O ( 1 ) O(1) O(1) 个决策需要单点修改时才能优化)
那么很快想到改成 f i f_i fi 一维状态,钦定 i i i 必选,往前找一个合法的,发现可以接上去的区间可以预处理出来,那么只需找 [ l , r ] [l,r] [l,r] 内小于 a i a_i ai 的最优决策… 三维偏序?树套树警告!
算了,先打暴力,竟然有 O ( 1 ) p t s O(1) pts O(1)pts 的高分,然鹅被一个 sb 细节卡住一直到 9:30 仍没调过,决定先看 T3
一眼发现是 sb 题,直接树上主席树就做完了,直接决定开码,10:30 过了小样例
然鹅大样例又挂了,反复调根本不明白怎么回事,一度以为自己主席树板子假了
最后突然想着把数组开大一倍,卧槽对了,不爆 RE 直接 WA 是吧,浪费了高达 O ( n ) O(n) O(n) 的时间
11:00 了,先把 T1 暴力调了吧,发现弱智错误… 然后看看能不能写点性质,得到了高达 5 p t s 5pts 5pts 的性质分
最后想 T2 感觉写不完,决定开 T4 暴力
最后获得了高达 7 p t s 7pts 7pts 的暴力分,赢!
所以 100+53+100+7=260 , rk O ( 2 n ) O(2^n) O(2n)
题解
T2


其实离正解不远了,回顾一下转移:
f i = m a x ( f j + 1 ) f_i=max(f_j+1) fi=max(fj+1),其中 j < i , a j < a i j<i,a_j<a_i j<i,aj<ai 且 i , j i,j i,j 可以通过小于 a i a_i ai 的数 “连接” 起来
直接三维偏序做也没错,但是本题可以有更多性质
注意到:能转移的决策满足 a j < a i a_j<a_i aj<ai,能连接其它数的数也是 a j < a i a_j<a_i aj<ai ,二者可以同时维护
那么我们转到值域上做,从小到大插入新决策
每次处理询问时相当于要找连续段,这个可以 s e t set set 做(更好做法是并查集,但是我不会);然后询问区间 Max,线段树维护
遇到偏序问题可以尝试 在最外层换一维关键字排序,会有意想不到的效果
#include<bits/stdc++.h>
using namespace std ;typedef long long LL ;
const int N = 3e5+100 ;int n , D , a[N] ;
int f[N] , rhk[N] ;
struct Segtree
{int l , r , Max ;
}t[4*N] ;
bool cmp( int x , int y )
{return a[x] < a[y] ;
}
void build( int p , int l , int r )
{t[p].l = l , t[p].r = r ;if( l == r ) {return ;}int mid = ( l + r ) >> 1 ;build( p<<1 , l , mid ) ; build( p<<1|1 , mid+1 , r ) ;
}
int ask( int p , int l , int r )
{if( l <= t[p].l && t[p].r <= r ) {return t[p].Max ;}int mid = ( t[p].l + t[p].r ) >> 1 , Max = 0 ;if( l <= mid ) Max = max( Max , ask(p<<1,l,r) ) ;if( r > mid ) Max = max( Max , ask(p<<1|1,l,r) ) ;return Max ;
}
void modify( int p , int x , int d )
{if( t[p].l == t[p].r ) {t[p].Max = max( t[p].Max , d ) ;return ;}int mid = ( t[p].l + t[p].r ) >> 1 ;if( x <= mid ) modify( p<<1 , x , d ) ;else modify( p<<1|1 , x , d ) ;t[p].Max = max( t[p<<1].Max , t[p<<1|1].Max ) ;
}
struct node
{int l , r ;friend bool operator < ( node x , node y ) {return x.r < y.r ;}
};
set<node> s ; // 维护连续段
int query( int x ) // 查 x 可用决策
{int P = max(1,x-D) ;auto it = s.lower_bound((node){0,P}) ;if( it == s.end() ) {return 0 ;}return ask( 1 , min(it->l,P) , x-1 ) ;
}
void Insert( int x )// 插入决策 x
{modify( 1 , x , f[x] ) ;if( s.empty() ) {s.insert((node){x,x}) ;return ;}auto it = s.lower_bound((node){0,x}) ;int L = x , R = x , fg = 0 ;if( it != s.end() ) {if( x < it->l ) {if( x+D >= it->l ) {// 接上了R = it->r ;fg = 1 ;} if( it != s.begin() ) {auto iit = it ;iit -- ;if( iit->r + D >= x ) {L = iit->l ;s.erase( iit ) ;}}if( fg ) s.erase( it ) ;s.insert((node){L,R}) ;}return ;}it -- ;if( it->r+D >= x ) {L = it->l ;s.erase( it ) ;}s.insert((node){L,x}) ;
}int main()
{scanf("%d%d" , &n , &D ) ;for(int i = 1 ; i <= n ; i ++ ) {scanf("%d" , &a[i] ) ; rhk[i] = i ;}// 转移有两维限制,按值域做,去掉一维sort( rhk+1 , rhk+n+1 , cmp ) ;build( 1 , 1 , n ) ;int ans = 0 ;for(int i = 1 ; i <= n ; i ++ ) {int j = i ;f[rhk[i]] = query( rhk[i] ) + 1 ;while( j+1 <= n && a[rhk[j]] == a[rhk[j+1]] ) {j ++ ;f[rhk[j]] = query( rhk[j] ) + 1 ;}for(int k = i ; k <= j ; k ++ ) {Insert( rhk[k] ) ;}i = j ;}for(int i = 1 ; i <= n ; i ++ ) {ans = max( ans , f[i] ) ;}printf("%d" , ans ) ;return 0 ;
}
其实很好写
T4
神奇题

尝试 d p dp dp ,发现根本做不了…
根据我们的经验,遇到十分之抽象且题面又臭又长又不知所云的题目大多是图论,所以这题考虑建图
额
老师讲的一个建图出发点:注意到最终序列中每个值 要么由 a a a 提供,要么由 b b b,这种 “由 A 或由 B” 的问题是有二分图的样子的,考虑分左右两部,对于每个 i i i,将左部 a i a_i ai 与 右部 b i b_i bi 连边
我理解的:题目中给的 划分 实际上约束是很多的,我们考虑最初选所有 a a a 中的集合,然后用 b b b 中的若干个集合替换,这样 替换者的并 和 被替换者的并 必须是一样的,想换掉某个子集 a [ ] a[] a[] 的话,必须选择 所有 包含 b b b 中对应位置 的区间,然后对应回来 a a a 中区间也必须选… 如此往复(口胡)
我们尝试形式化的去描述这个东西,发现正可以用上面那种建边方式来描述 ,一个连通块就代表了 可以相互替换的一组 a [ ] , b [ ] a[],b[] a[],b[]
对于 K = 0 K=0 K=0,我们直接对于每个连通块取较小的那一组替换
对于 K = 1 K=1 K=1,考虑枚举边,分讨一下:
若断的是非割边,然后连到另一个连通块,这样贡献的变化是 m i n ( a , b ) + m i n ( c , d ) → m i n ( a + c , b + d ) min(a,b)+min(c,d)\to min(a+c,b+d) min(a,b)+min(c,d)→min(a+c,b+d)
显然有不等式 m i n ( a , b ) + m i n ( c , d ) ≤ m i n ( a + c , b + d ) min(a,b)+min(c,d)\leq min(a+c,b+d) min(a,b)+min(c,d)≤min(a+c,b+d),所以贡献不会变小,断开一定不优
这个不等式也告诉我们,要尽可能拆连通块,尽可能不合并连通块
若断割边,我们最好的当然是连回本身,只拆,不合并
注意!这里有一个 conner,如果一个连通块只有两个节点 u , v u,v u,v 怎么办?我们显然没办法把 u u u 向自己连边
然而有这么一个事情:不妨设 u u u 为左部点,那么一定可以把 u u u 连到一个 左部点数不小于右部点的连通块上(找不到的话考虑右部点 v v v ),当 n ≥ 1 n\geq 1 n≥1 时,这样的连通块一定能找到
当 n = 1 n=1 n=1,直接特判 答案为 1 1 1 即可
对于 K = 2 K=2 K=2,与上面相反,需要 尽可能合并连通块,尽可能不拆连通块
对于一个连通块,如果有 非割边 ,那么用它一定比用割边更优,因为不会拆,且能够合并
下面考虑应该和哪个连通块合并,对于两个连通块 ( a 1 , b 1 ) (a_1,b_1) (a1,b1) , ( a 2 , b 2 ) (a_2,b_2) (a2,b2)
若 a 1 < b 1 , a 2 < b 2 a_1<b_1,a_2<b_2 a1<b1,a2<b2 (不等号方向相同):
贡献变化 m i n ( a 1 + a 2 , b 1 + b 2 ) − m i n ( a 1 , b 1 ) − m i n ( a 2 , b 2 ) = 0 min(a_1+a_2,b_1+b_2)-min(a_1,b_1)-min(a_2,b_2)=0 min(a1+a2,b1+b2)−min(a1,b1)−min(a2,b2)=0,没影响
若 a 1 < b 1 , a 2 > b 2 a_1<b_1,a_2>b_2 a1<b1,a2>b2 (相反)
贡献变化 m i n ( a 1 + a 2 , b 1 + b 2 ) − m i n ( a 1 , b 1 ) − m i n ( a 2 , b 2 ) min(a_1+a_2,b_1+b_2)-min(a_1,b_1)-min(a_2,b_2) min(a1+a2,b1+b2)−min(a1,b1)−min(a2,b2)
= m i n ( a 1 + a 2 , b 1 + b 2 ) − a 1 − b 2 =min(a_1+a_2,b_1+b_2)-a_1-b_2 =min(a1+a2,b1+b2)−a1−b2
= m i n ( a 2 − b 2 , b 1 − a 1 ) =min(a_2-b_2,b_1-a_1) =min(a2−b2,b1−a1)
= m i n ( Δ 1 , Δ 2 ) =min(\Delta_1,\Delta_2) =min(Δ1,Δ2)
当 a 1 , b 1 a_1,b_1 a1,b1 确定时,要找一个不等号相反,且差最大的,直接扫一遍记 Max 就行
如果全是割边,我们直接遍历这棵缩点后的树,依次断开每条树边即可
不太好写
#include<bits/stdc++.h>
using namespace std ;typedef long long LL ;
const int N = 2e5+100 ; int T , K , M1 , M2 ;
int n , a[N] , b[N] ;
struct nn
{int lst , to ;
}E[2*N] ;
int head[2*N] , tot = 1 ;
inline void add( int x , int y )
{E[++tot] = (nn){ head[x] , y } ;head[x] = tot ;
}
int dfn[2*N] , low[2*N] , tim ;
bool bri[2*N] ;
vector<int> e[2*N] ;
void tarjan( int x , int inE )
{dfn[x] = low[x] = ++tim ;for(int i = head[x] ; i ; i = E[i].lst ) {int t = E[i].to ;if( !dfn[t] ) {tarjan( t , i ) ;low[x] = min( low[x] , low[t] ) ;if( low[t] > dfn[x] ) {bri[i] = bri[i^1] = 1 ;}}else if( i != (inE^1) ) {low[x] = min( low[x] , dfn[t] ) ;}}
}
int cnt , bol , bel[2*N] , A[2*N] , B[2*N] , SA[2*N] , SB[2*N] ;
void dfs( int x )
{bel[x] = cnt ;if( x <= M1 ) A[cnt] ++ ;else B[cnt] ++ ;for(int i = head[x] ; i ; i = E[i].lst ) {int t = E[i].to ;if( bri[i] ) {if( bel[t] ) {e[bel[t]].push_back( bel[x] ) ;e[bel[x]].push_back( bel[t] ) ;}}else if( !bel[t] ) dfs( t ) ;}
}
int PA[2*N] , PB[2*N] , ans1 , ans2 , ans3 , rt[2*N] ;
bool can[2*N] ; // 是否有非割边
void get_size( int x , int fa )
{SA[x] = A[x] , SB[x] = B[x] ;if( A[x]+B[x] > 1 ) can[bol] = 1 ;for(int t : e[x] ) {if( t == fa ) continue ;get_size( t , x ) ;SA[x] += SA[t] ; SB[x] += SB[t] ;}
}
void ddfs( int x , int fa )
{for(int t : e[x] ) {if( t == fa ) continue ;ans2 = max( ans2 , min(PA[bol],PB[bol])-min(SA[t],SB[t])-min(PA[bol]-SA[t],PB[bol]-SB[t]) ) ; // 最多减少多少 ddfs( t , x ) ;}
}
int I , Mx1 , Mx2 ;
inline int V ( int a , int b , int c , int d ) // 合并后增加多少 / 拆开后损失多少
{return min(a+c,b+d)-min(a,b)-min(c,d) ;
}
inline int V1( int a , int b )
{if( a > b ) return min(a-b,Mx2) ;return min(b-a,Mx1) ;
}
void Get( int x , int fa ) // 处理割边
{for(int t : e[x] ) {if( t == fa ) continue ;ans3 = max( ans3 , -V(SA[t],SB[t],PA[I]-SA[t],PB[I]-SB[t])+V1(SA[t],SB[t]) ) ;ans3 = max( ans3 , -V(SA[t],SB[t],PA[I]-SA[t],PB[I]-SB[t])+V1(PA[I]-SA[t],PB[I]-SB[t]) ) ;Get( t , x ) ;}
}
void solve()
{cnt = 0 ; bol = 0 ;for(int i = 1 ; i <= M1+M2 ; i ++ ) {if( !dfn[i] ) {tarjan( i , 0 ) ;}}for(int i = 1 ; i <= M1+M2 ; i ++ ) {if( !bel[i] ) {cnt ++ ;dfs( i ) ;}}ans1 = ans2 = ans3 = 0 ;for(int i = 1 ; i <= cnt ; i ++ ) {if( !SA[i]&&!SB[i] ) {bol ++ ;rt[bol] = i ;get_size( i , 0 ) ;PA[bol] = SA[i] , PB[bol] = SB[i] ;ddfs( i , 0 ) ;ans1 += min(PA[bol],PB[bol]) ;}}ans2 = ans1-ans2 ;if( K == 0 ) {printf("%d\n" , ans1 ) ;return ;}if( K == 1 ) {printf("%d\n" , ans2 ) ;return ;}if( K == 2 ) {Mx1 = 0 , Mx2 = 0 ;if( M1 < n ) Mx1 = 1 ;if( M2 < n ) Mx2 = 1 ;for(int i = 1 ; i <= bol ; i ++ ) {Mx1 = max( Mx1 , PA[i]-PB[i] ) ;Mx2 = max( Mx2 , PB[i]-PA[i] ) ;}for(int i = 1 ; i <= bol ; i ++ ) {if( can[i] ) {if( PA[i] > PB[i] ) ans3 = max( ans3 , min(PA[i]-PB[i],Mx2) ) ;else ans3 = max( ans3 , min(PB[i]-PA[i],Mx1) ) ;}else {I = i ;Get( rt[i] , 0 ) ;}}printf("%d\n" , ans3+ans1 ) ;return ;}
}
int nam[N][2] ;
void Clear()
{for(int i = 2 ; i <= tot ; i ++ ) bri[i] = 0 ;tot = 1 ;for(int i = 1 ; i <= M1+M2 ; i ++ ) head[i] = dfn[i] = bel[i] = 0 ;for(int i = 1 ; i <= n ; i ++ ) nam[i][0] = nam[i][1] = 0 ;tim = 0 ; for(int i = 1 ; i <= cnt ; i ++ ) e[i].clear() , A[i] = B[i] = SA[i] = SB[i] = 0 ;for(int i = 1 ; i <= bol ; i ++ ) can[i] = 0 ;
}int main()
{scanf("%d%d" , &T , &K ) ;while( T -- ) {scanf("%d" , &n ) ;if( n == 1 ) {printf("1\n") ;for(int i = 1 ; i <= n ; i ++ ) scanf("%d" , &a[i] ) ;for(int i = 1 ; i <= n ; i ++ ) scanf("%d" , &b[i] ) ;continue ;}M1 = 0 , M2 = 0 ;for(int i = 1 ; i <= n ; i ++ ) {scanf("%d" , &a[i] ) ;if( !nam[a[i]][0] ) {nam[a[i]][0] = ++M1 ;}a[i] = nam[a[i]][0] ;}for(int i = 1 ; i <= n ; i ++ ) {scanf("%d" , &b[i] ) ;if( !nam[b[i]][1] ) {nam[b[i]][1] = ++M2 ;}b[i] = nam[b[i]][1] ;add( a[i] , b[i]+M1 ) , add( b[i]+M1 , a[i] ) ;}solve() ;Clear() ;}return 0 ;
}
相关文章:

7.23模拟赛总结 [数据结构优化dp] + [神奇建图]
目录 复盘题解T2T4 复盘 浅复盘下吧… 7:40 开题 看 T1 ,起初以为和以前某道题有点像,子序列划分,注意到状态数很少,搜出来所有状态然后 dp,然后发现这个 T1 和那个毛关系没有 浏览了一下,感觉 T2 题面…...

MySQL-视 图
视 图 创建视图 视图是从一个或者几个基本表(或视图)导出的表。它与基 本表不同,是一个虚表。 语法: create view 视图名 【view_xxx/v_xxx】 说明: • view_name 自己定义的视图名; • as 后面是这…...

PHP SimpleXML
PHP SimpleXML PHP的SimpleXML扩展提供了一个非常方便的方式来处理XML数据。它是PHP内置的,因此不需要安装额外的库。SimpleXML可以将XML数据转换成对象,使得操作XML变得简单直观。本文将详细介绍SimpleXML的使用方法,包括加载XML、访问和修…...

【Spring Boot 自定义配置项详解】
文章目录 一、配置文件1. properties配置1.1 创建配置文件1.2 添加配置项1.3 在应用中使用配置项1.4 多环境配置 2. YAML配置2.1 创建配置文件2.2 添加配置项2.3 在应用中使用配置项2.4 多环境配置 二、自定义配置类1. 创建配置类2. 使用配置类 一、配置文件 Spring Boot支持多…...
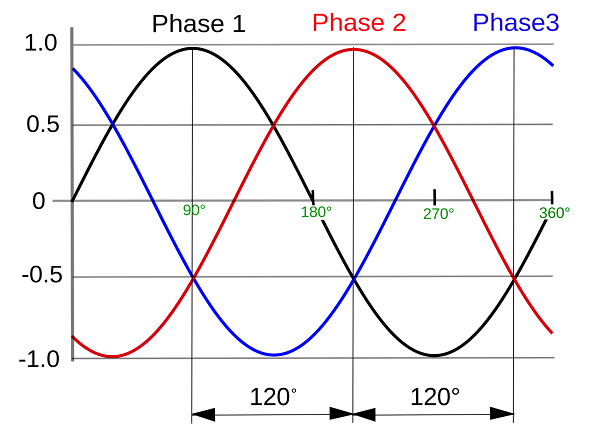
电机相位接线错误导致的潜在问题
交流电机有两种基本类型:单相和三相。一般来说,单相交流电机通常用于家用电器等住宅应用,而三相交流电机则用于工业应用。这主要是因为大多数家庭使用单相电源,而大多数工业场所使用三相电源。 鉴于这两种不同的电源方案…...

react中如何mock数据
1.需求说明 因为前后端分离开发项目,就会存在前端静态页面写好了,后端数据接口还没写好;这时候前端就需要自己定义数据来使用。 定义数据有三种方式:直接写死数据、使用mock软件、json-server工具 这里讲解通过json-server工具…...

通过Faiss和DINOv2进行场景识别
目标:通过Faiss和DINOv2进行场景识别,确保输入的照片和注册的图片,保持内容一致。 MetaAI 通过开源 DINOv2,在计算机视觉领域取得了一个显着的里程碑,这是一个在包含1.42 亿张图像的令人印象深刻的数据集上训练的模型…...

新手入门基础Java
一:基础语法 1.Java的运行机制 2. Java基本语法 1.注释、标识符、关键字; 2.数据类型(四类八种) 3.类型转换 1.自动转换;2.强制转换; 4.常量和变量 1.常量;2.变量; 3.变量的作用域 5.运算符 1.算数运算符;2.赋值运算符;3.关系运算符; 4.逻辑运算符;5.自…...

2024最新版虚拟便携空调小程序源码 支持流量主切换空调型号
产品截图 部分源代码展示 urls.js Object.defineProperty(exports, "__esModule", {value: !0 }), exports.default ["9c5f1fa582bee88300ffb7e28dce8b68_3188_128_128.png", "E-116154b04e91de689fb1c4ae99266dff_960.svg", "573eee719…...

前端在浏览器总报错,且获取请求头中token的值为null
前端请求总是失败说受跨域请求影响,但前后端配置已经没有问题了,如下: package com.example.shop_manage_sys.config;import org.springframework.beans.factory.annotation.Autowired; import org.springframework.context.annotation.Conf…...

html+css前端作业 王者荣耀官网6个页面无js
htmlcss前端作业 王者荣耀官网6个页面无js 下载地址 https://download.csdn.net/download/qq_42431718/89571150 目录1 目录2 项目视频 王者荣耀6个页面(无js) 页面1 页面2 页面3 页面4 页面5 页面6...

在windows上使用Docker部署一个简易的web程序
使用Docker部署一个python的web服务🚀 由于是从事算法相关工作,之前在项目中,需要将写完的代码服务,部署在docker上,以此是开始接触了Docker这个工具,由于之前也没系统学习过,之后应该可能还会用…...

sqlalchemy使用mysql的json_extract函数查询JSON字段
sqlalchemy使用mysql的json_extract函数查询JSON字段 在SQLAlchemy中,如果你想要在MySQL中存储JSON字段,并且进行查询操作,可以按照以下步骤进行设置和查询: 1. 创建表格 首先,创建一个表格来存储包含JSON字段的数据。假设我们有一个名为 users 的表格,其中有一个名为…...

分类模型-逻辑回归和Fisher线性判别分析★★★★
该博客为个人学习清风建模的学习笔记,部分课程可以在B站:【强烈推荐】清风:数学建模算法、编程和写作培训的视频课程以及Matlab等软件教学_哔哩哔哩_bilibili 目录 1理论 1.1逻辑回归模型 1.2线性概率模型 1.3线性判别分析 1.4两点分布…...
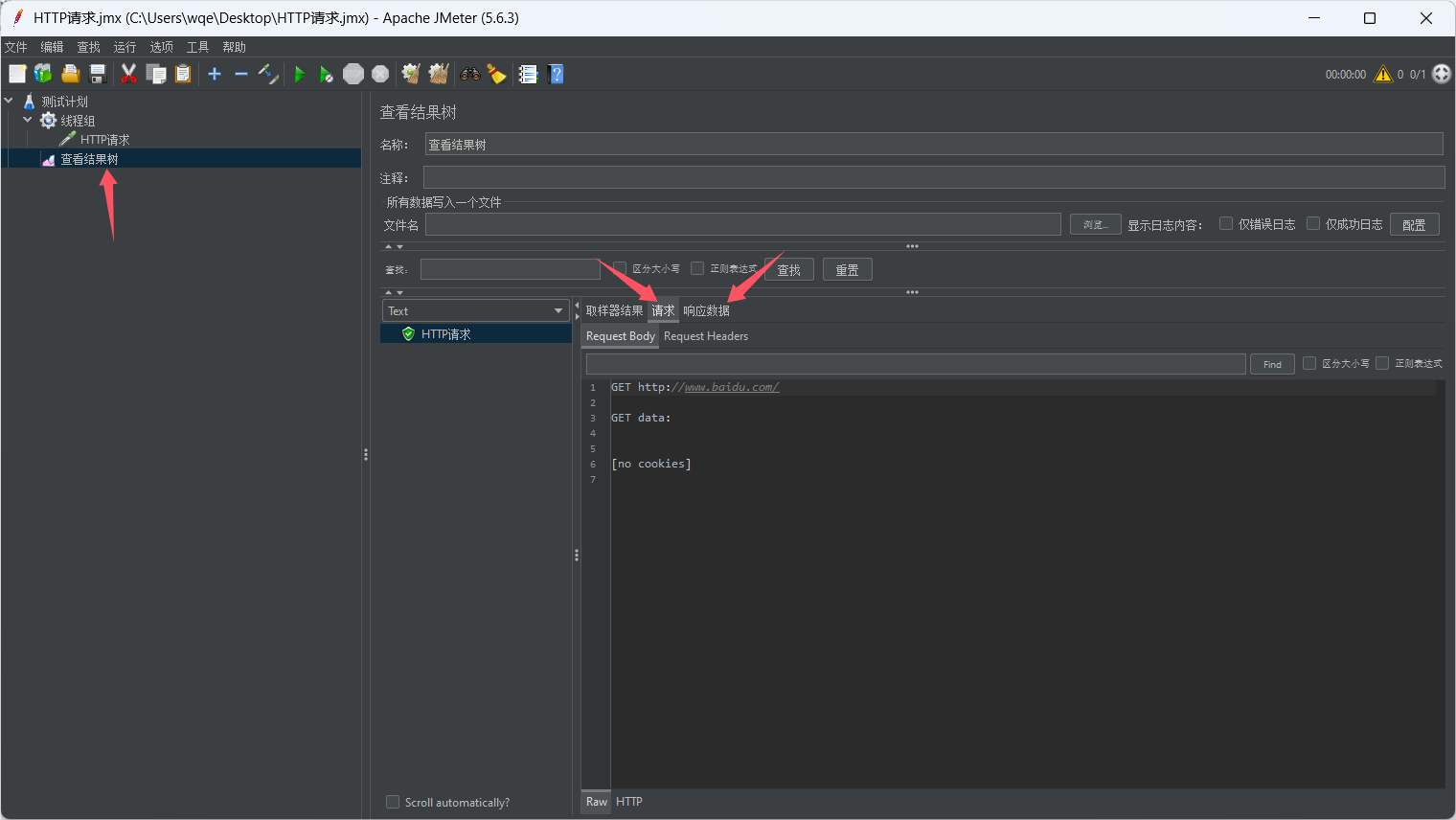
JMeter介绍、安装配置以及快速入门
文章目录 1. JMeter简介2. JMeter安装配置3. JMeter快速入门 1. JMeter简介 Apache JMeter是一款开源的压力测试工具,主要用于测试静态和动态资源(如静态文件、服务器、数据库、FTP服务器等)的性能。它最初是为测试Web应用而设计的ÿ…...

GPT LangChain experimental agent - allow dangerous code
题意:GPT LangChain 实验性代理 - 允许危险代码 问题背景: Im creating a chatbot in VS Code where it will receive csv file through a prompt on Streamlit interface. However from the moment that file is loaded, it is showing a message with…...

1 LableMe安装下载
git:GitHub - labelmeai/labelme: Image Polygonal Annotation with Python (polygon, rectangle, circle, line, point and image-level flag annotation). 1 LabelMe介绍 LabelMe是一个图像标注工具,主要用于帮助研究人员和开发者创建有标签的数据集,这…...

rce漏洞-ctfshow(50-70)
Web51 if(!preg_match("/\;|cat|flag| |[0-9]|\\$|\*|more|less|head|sort|tail|sed|cut|tac|awk|strings|od|curl|\|\%|\x09|\x26/i", $c)){ system($c." >/dev/null 2>&1"); } Nl,绕过tac,cat,绕…...

vulntarget-a靶机-复现报告
靶机复现过程 测试标题 测试过程 测试外网ip 192.168.2.84 测试详情 第一步,我们先对其这个外网ip进行扫描,结果如下 结果我们发现这个ip开启了80和445端口,同时我们还可以看到这里是win7系统,我们先看看web页面是怎样的 结…...
为什么 FPGA 的效率低于 ASIC?
FPGA是“可重构逻辑”器件。先制造的芯片,再次设计时“重新配置”。 ASIC 不需要“重新配置”。你先设计,把它交给代工厂,然后制造芯片。 现在让我们看看这些芯片的结构是什么样的,以及它们的不同之处。 ● 逻辑单元:F…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
