【安全】系统安全设计规范(DOC完整版)
1.1安全建设原则
1.2 安全管理体系
1.3 安全管理规范
1.4 数据安全保障措施
1.4.1 数据库安全保障
1.4.2 操作系统安全保障
1.4.3 病毒防治
1.5安全保障措施
1.5.1实名认证保障
1.5.2 接口安全保障
1.5.3 加密传输保障
1.5.4终端安全保障
软件资料清单列表部分文档:
工作安排任务书,可行性分析报告,立项申请审批表,产品需求规格说明书,需求调研计划,用户需求调查单,用户需求说明书,概要设计说明书,技术解决方案,数据库设计说明书,详细设计说明书,单元测试报告,总体测试计划,单元测试计划,产品集成计划,集成测试报告,集成测试计划,系统测试报告,产品交接验收单,验收报告,验收测试报告,压力测试报告,项目总结报告,立项结项审批表,成本估算表,项目计划,项目周报月报,风险管理计划,质量保证措施,项目甘特图,项目管理工具,操作手册,接口设计文档,软件实施方案,运维方案,安全检测报告,投标响应文件,开工申请表,开工报告,概要设计检查表,详细设计检查表,需求规格说明书检查表,需求确认表,系统代码编写规范,软件项目质量保证措施,软件部署方案,试运行方案,培训计划方案,软件系统功能检查表,工程试运行问题报告,软件合同,资质评审材料,信息安全相关文档等。
获取方式:本文末个人名片直接获取。












相关文章:

【安全】系统安全设计规范(DOC完整版)
1.1安全建设原则 1.2 安全管理体系 1.3 安全管理规范 1.4 数据安全保障措施 1.4.1 数据库安全保障 1.4.2 操作系统安全保障 1.4.3 病毒防治 1.5安全保障措施 1.5.1实名认证保障 1.5.2 接口安全保障 1.5.3 加密传输保障 1.5.4终端安全保障 软件资料清单列表部分文档&…...

windows常用命令整理
本文分享一些常用的windows命令。根据功能的不同,大致可分为以下几个方面,一是文件操作命令,二是进程相关命令,三是磁盘相关命令,四是网络相关命令,五是其他命令。 1.文件操作命令 dir:显示当…...

视频处理基础知识1
1、图像基本知识 图像的组成:像素、RGB(每个像素由三个发光二极管组成)、分辨率(横纵向像素的个数乘积) PPI每英寸的像素数 DPI每英寸的点数,有可能一个点有多个像素 PPI>300 就属于视网膜级别,就是很清晰&#…...

Linux退不出vim编辑模式
目录 第一章、问题分析1.1)报错提示 第二章、解决方式 友情提醒: 先看文章目录,大致了解文章知识点结构,点击文章目录可直接跳转到文章指定位置。 第一章、问题分析 1.1)报错提示 报错如下:使用Linux的vi…...

TikTok养号的网络环境及相关代理IP知识
TikTok作为一个流行的短视频分享平台,其用户量非常庞大,很多商家和个人都会使用TikTok来进行引流和推广。由于TikTok的规则和政策限制了每个用户每天发布视频的数量,因此许多用户会使用多个账号来发布更多的视频以提高曝光率。 然而ÿ…...

过程调用和数组的分配访问
系列文章 : 深入理解计算机系统笔记 文章目录 系列文章3.7 过程3.7.1 运行时栈3.7.2 转移控制3.7.3 数据传送3.7.4 栈上的局部存储3.7.5 寄存器中的局部存储空间3.7.6 递归过程 3.8 数组分配和访问3.8.1 基本原则3.8.2 指针运算3.8.3 嵌套的数组3.8.4 定长数组3.8.5 变长数组…...

TeamViewer手机端APP提示:请先验证账户
当你在手机端下载安装了TeamViewerAPP后,需要你先登录个人账号,然后还会要求你验证账户,同时跳转到一个网址中,但是这个网址并没有自动跳转到验证账户的位置。 解决办法: 在手机浏览器中进入下面这个网址:…...

【SpringBoot】分页查询
1. Controller ApiOperation("分页查询")GetMapping("/page")public Result<PageResult> pageResultResult(EmployeePageQueryDTO employeePageQueryDTO) {System.out.println(employeePageQueryDTO.toString());PageResult pageResult employeeSer…...
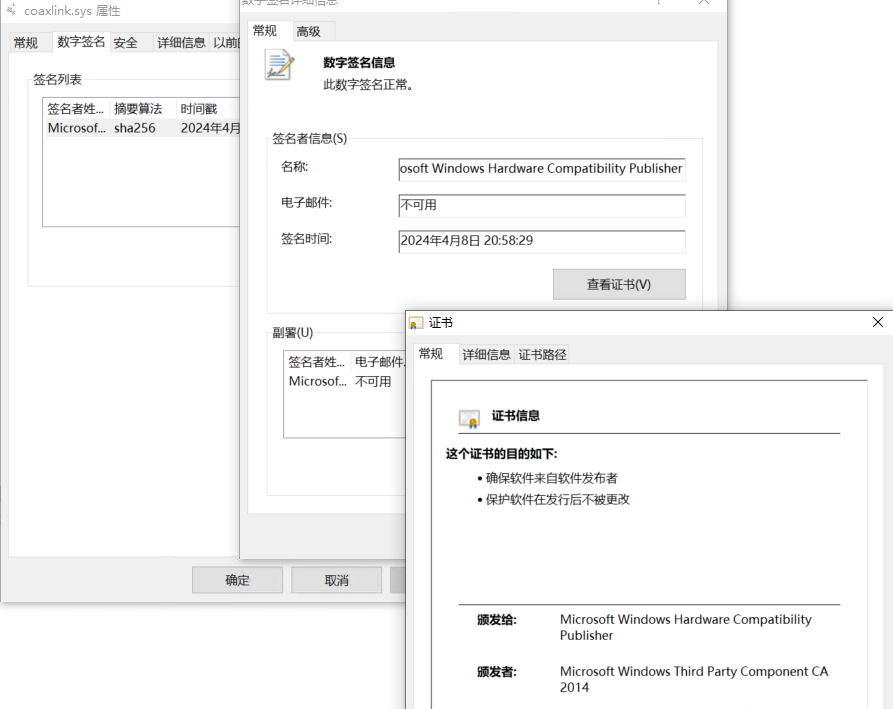
微软CrowdStrike驱动蓝屏以及内核签名
原因 当Windows操作系统遇到严重错误导致系统崩溃时,屏幕显示为蓝色,通常伴有错误代码和信息,这被称为“蓝屏死机”(Blue Screen of Death,简称BSOD) https://www.thepaper.cn/newsDetail_forward_281262…...
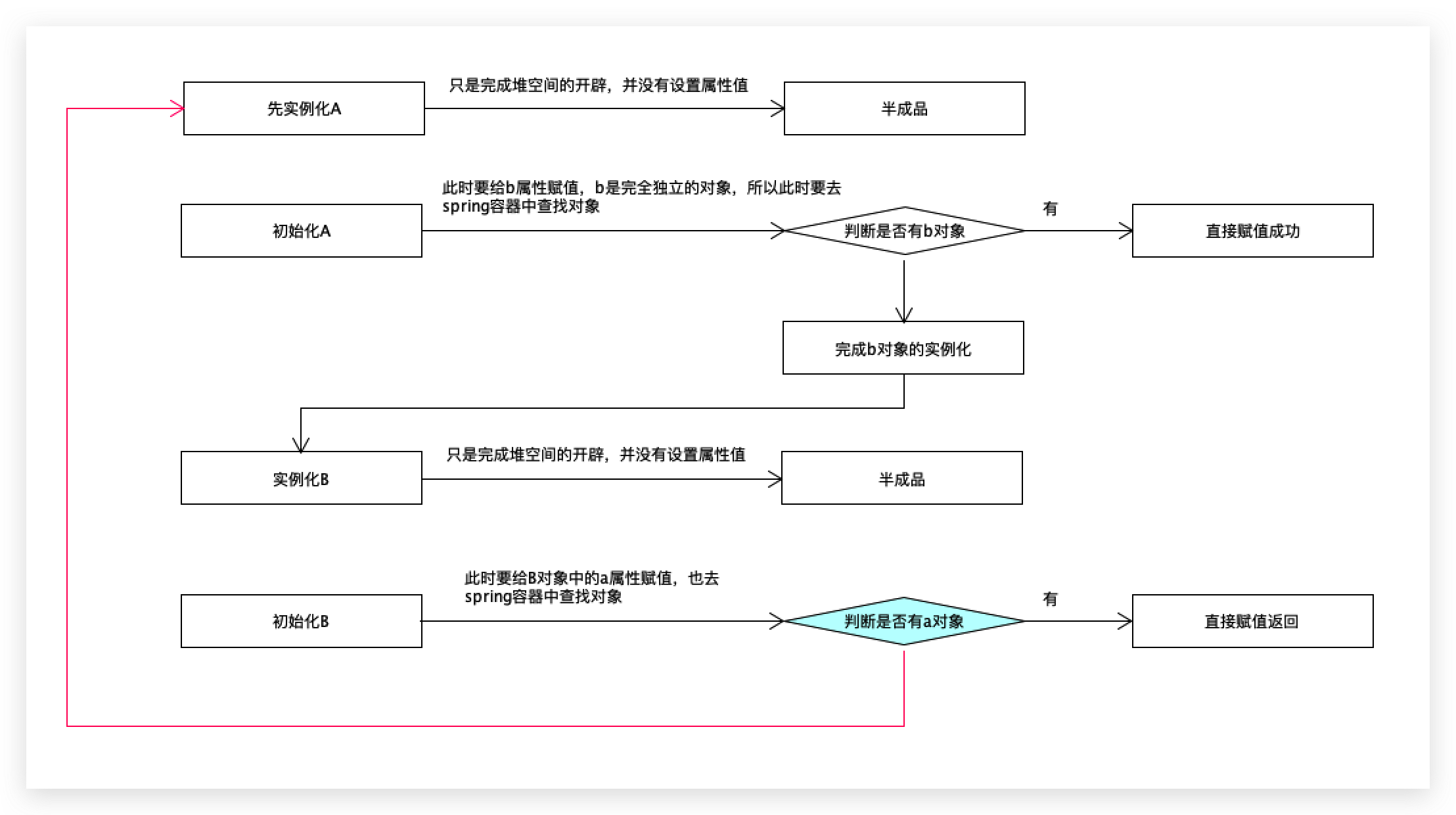
Spring中Bean的循环依赖
目录 定义: 循环依赖的后果: 一:三级缓存 1、大概的思路: 注意: 2、执行过程: A半完成: B完成: A完成: 注: 二:Lazy 定义: …...

Java二十三种设计模式-代理模式模式(8/23)
代理模式:为对象访问提供灵活的控制 引言 代理模式(Proxy Pattern)是一种结构型设计模式,它为其他对象提供一个代替或占位符,以控制对它的访问。 基础知识,java设计模式总体来说设计模式分为三大类&#…...

Windows 11 家庭中文版 安装 VMWare 报 安装程序检测到主机启用了Hyper-V或Device
1、问题 我的操作系统信息如下: 我在安装 VMWare 的时候,报: 因为我之前安装了 docker 桌面版,所以才报这个提示。 安装程序检测到主机启用了 Hyper-v或 Device/credential Guard。要在启用了Hyper-或 Device/Credential Guard …...

机械学习—零基础学习日志(高数09——函数图形)
零基础为了学人工智能,真的开始复习高数 函数图像,开始新的学习! 幂函数 利用函数的性质,以幂函数为例,因为单调性相同,利用图中的2和3公式,求最值问题,可以直接将式子进行简化。这…...

java迭代集合出现并发修改异常(ConcurrentModificationException)的原因以及解决方案
java迭代集合出现并发修改异常(ConcurrentModificationException)的原因以及解决方案 一. 什么时候会出现并发修改异常? 这里先看需求 : 定义一个集合,存储 唐僧,孙悟空,猪八戒,沙僧,遍历集合,如果遍历到猪八戒,往集合中添加一个白龙马 很显然要求我们先创建一个集合并进行…...

BGP选路之Local Preference
原理概述 当一台BGP路由器中存在多条去往同一目标网络的BGP路由时,BGP协议会对这些BGP路由的属性进行比较,以确定去往该目标网络的最优BGP路由。BGP首先比较的是路由信息的首选值(PrefVal),如果 PrefVal相同,就会比较本…...

WEB渗透信息收集篇--IP和端口信息
WEB渗透信息收集篇--域名信息-CSDN博客 WEB渗透信息收集篇--网站架构和指纹识别-CSDN博客 WEB渗透信息收集篇--人员信息-CSDN博客 WEB渗透信息收集篇--其他信息-CSDN博客 一、ASN ASN Tool - MxToolBox ASN通常指的是"自…...

国内微短剧系统平台抖音微信付费小程序app开发源代码交付
微短剧作为当下热门的内容,结合抖音平台的广泛用户基础,开发微短剧付费小程序APP具有显著的市场潜力,用户对于短剧内容的需求旺盛,特别是在言情、总裁、赘婿等热门题材方面,接下来给大家普及一下微短剧小程序系统。 顺…...

Java语言程序设计基础篇_编程练习题**15.19 (游戏:手眼协调)
**15.19 (游戏:手眼协调) 请编写一个程序,显示一个半径为10像素的实心圆,该圆放置在面板上的随机位置,并填充随机的顔色,如图15-29b所示。单击这个圆时,它会消失,然后在另一个随机的位置显示新的随机颜色的…...

学习记录day16—— 数据结构 双向链表 循环链表
双向链表 1、概念 1)就是从任意一个节点既能存储其前驱节点,又能存储后继节点 2)结构体中增加一个指向前驱节点的指针 //定义数据类型 typedef int datatype;//定义节点类型 typedef struct Node {union {int len;datatype data;};struct Node *prio; …...

Air780EP模块 AT开发-MQTT接入OneNET移动物联网平台应用指南
应用概述 使用AT方式通过MQTT协议连接onenet studio。官网地址:https://open.iot.10086.cn/ 材料准备 Air780EP(V)开发板一套,包括天线SIM卡,USB线。 PC电脑,串口工具 在onenet上创建产品 打开OneNET官网,进入控制…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
