【数据结构】建堆算法复杂度分析及TOP-K问题
【数据结构】建堆算法复杂度分析及TOP-K问题

🔥个人主页:大白的编程日记
🔥专栏:数据结构
文章目录
- 【数据结构】建堆算法复杂度分析及TOP-K问题
- 前言
- 一.复杂度分析
- 1.1向下建堆复杂度
- 1.2向上建堆复杂度
- 1.3堆排序复杂度
- 二.TOP-K问题
- 2.1思路分析
- 2.2代码实现
- 后言
前言
哈喽,各位小伙伴大家好!上期我们讲了堆排序和建堆算法。今天我们就来分析一下他们的时间复杂度。话不多说,咱们进入正题。向大厂冲锋!
一.复杂度分析
我们都知道堆是一个完全二叉树。那他的高度h和节点数量N有什么关系呢?

那我们再来对比一下满二叉树和完全二叉树的高度h.

我们用大O渐进表示法看的话他们两个的高度h都可以认为是logN的量级
所以我们的堆的上下调整可以认为是logN,也就是高度次。
因为堆是完全二叉树,而满二叉树也是完全二叉树,所以为了方便证明
我们使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个结点不影响最终结果):
1.1向下建堆复杂度
我们先分别算出第一层到h-1层的节点个数和该层节点的调整次数
然后再推出总的调整次数。
- 推导

1.2向上建堆复杂度
我们先分别算出第2层到h层的节点个数和该层节点的调整次数
然后再推出总的调整次数。
- 推导

所以向下建堆的时间复杂度是O(N),向上建堆的复杂度是O(N*logN).
所以以后我们都尽量使用向下调整建堆。因为他的效率更高。
1.3堆排序复杂度
现在我们来看一下我们堆排序的时间复杂度是多少呢?
- 推导

堆排序的复杂度是O(N*logN).
二.TOP-K问题
2.1思路分析
我们的堆除了可以用来排序还可以用来解决经典的TOP-K问题。
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
- 方法一
我们很容易想到直接排序然后取出前K个即可。
但是这个方法有个致命缺陷。
如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。

我们发现这个方法在数据量太大的时候并不适用。
那有什么其他好的方法吗? - 方法二
最佳的方式就是用堆来解决,基本思路如下:
1 .用数据集合中前K个元素来建堆
前k个最大的元素,则建K个数的小堆
前k个最小的元素,则建K个数的大堆
2 . 用剩余的N-K个元素依次与堆顶元素来比较,
如果比堆顶元素还要大或小(小堆大 大堆小)则替换堆顶元素,然后向下调整重新建堆。
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
为什么呢?
- 证明

我们通过N-K次比较就可以筛选出N-K个不满足最大前K个数的数
剩下在堆的数就是最大的前K个。 - 疑问

我们用反证法可以得知这种情况不存在。
2.2代码实现
- 生成数据函数
我们先用srand生成不同的种子防止生成的随机数是伪随机数。
然后fopen打开文件。循环生成随机数然后写入文件即可。最后关闭文件。
void CreatData()
{int n = 100000;//生成10万个数据srand(time(0));//生成不同的种子FILE* pf = fopen("test.txt", "w");//打开文件for (int i = 0; i < n; i++){int x = rand() % 100001+i;//生成随机数fprintf(pf, "%d\n", x);//写数据}fclose(pf);//关闭文件pf = NULL;
}

这样10万个数据就生成好了。
- 比较函数
我们先接收k。然后开好k个数是堆空间。
然后从文件读取前k个数并填充到堆里面。然后建堆
然后继续读取文件里的数据直到文件末尾(返回EOF)
然后当数据大于堆顶元素是在进堆,然后重新调整建堆即可。
void test()
{int k;printf("请输入前K个数:");scanf("%d", &k);int* a = (int*)malloc(sizeof(int) * k);//开空间建堆FILE* pf = fopen("test.txt", "r");for (int i = 0; i < k; i++){fscanf(pf, "%d", &a[i]);}//填充数据for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, k, i);}//建小堆int x;while (fscanf(pf, "%d", &x) !=EOF){if (x > a[0]){a[0] = x;AdjustDown(a, k, 0);}}//对比for (int i = 0; i < k; i++){printf("%d ", a[i]);}//打印
}
- 检验

那我们如何确保这10个数一定是最大的呢?万一我们的算法写错不是最大的前10个数怎么办?










那我们就可以在不同的地方在一些k标点。
也就是K个很大的数,确保他们是最大的前K个。
然后只需要看结果是不是这k个数即可。

大家发现结果就是我们手动给的这10个数。说明我们的程序时没问题的。
后言
这就是建堆算法复杂度分析及TOP-K问题。这里涉及到许多数学知识。大家可以多看几遍证明图。今天就分享到这里。感谢大佬们垂阅!咱们下期见!拜拜~

相关文章:

【数据结构】建堆算法复杂度分析及TOP-K问题
【数据结构】建堆算法复杂度分析及TOP-K问题 🔥个人主页:大白的编程日记 🔥专栏:数据结构 文章目录 【数据结构】建堆算法复杂度分析及TOP-K问题前言一.复杂度分析1.1向下建堆复杂度1.2向上建堆复杂度1.3堆排序复杂度 二.TOP-K问…...

Thinkphp5实现前后端通过接口通讯基本操作方法
在ThinkPHP5框架中,实现前后端通过接口通讯是一个常见的需求,尤其是在开发RESTful API时。下面是一个基本的步骤指南,用于设置ThinkPHP5来创建API接口,并使前端能够通过HTTP请求与后端进行通讯。 1. 创建API模块 首先࿰…...

Go 语言任务编排 WaitGroup
WaitGroup 是常用的 Go 同步原语之一,用来做任务编排。它要解决的就是并发-等待的问题: 现在有一个 goroutine A 在检查点 ( checkpoint ) 等待一组 goroutine 全部完成它们的任务,如果这些 goroutine 还没全部完成任务,那么 goroutine A 就会被阻塞在检查点,直到所有的 …...

星环科技推出知识库产品 AI PC时代数据交互方式变革
随着企业业务的快速发展,数据量呈爆炸式增长,有效的知识管理成为企业面临的重要问题。企业遇到的普遍问题是大量的结构化、半结构化数据存储在不同的系统中,需要用多种计算机语言进行检索。而大模型彻底改变了人们和数据的交互方式࿰…...

10道JVM经典面试题
1、 JVM中,new出来的对象是在哪个区? 2、 说说类加载有哪些步骤? 3、 JMM是什么? 4、 说说JVM内存结构? 5、 MinorGC和FullGC有什么区别? 6、 什么是STW? 7、 什么情况下会发生堆/栈溢出?…...

Redisson常用的数据结构及应用场景
Redisson 提供了一系列高级数据结构,这些数据结构封装了 Redis 的原生数据类型,提供了 Java API 的便利性和分布式特性。以下是 Redisson 中一些常用的数据结构,场景还在不断完善中: RBucket:这是一个简单的键值对存储…...

【实现100个unity特效之8】使用ShaderGraph实现2d贴图中指定部分局部发光效果
最终效果 寒冰法师 火焰法师 文章目录 最终效果寒冰法师火焰法师 素材一、功能分析实现方法基本思路Unity的Bloom后处理为什么关键部位白色?最终结果 二、 新建URP项目三、合并图片四、使用PS制作黑白图片方法一 手动涂鸦方法二 魔棒工具1. 拖入图片进PS࿰…...
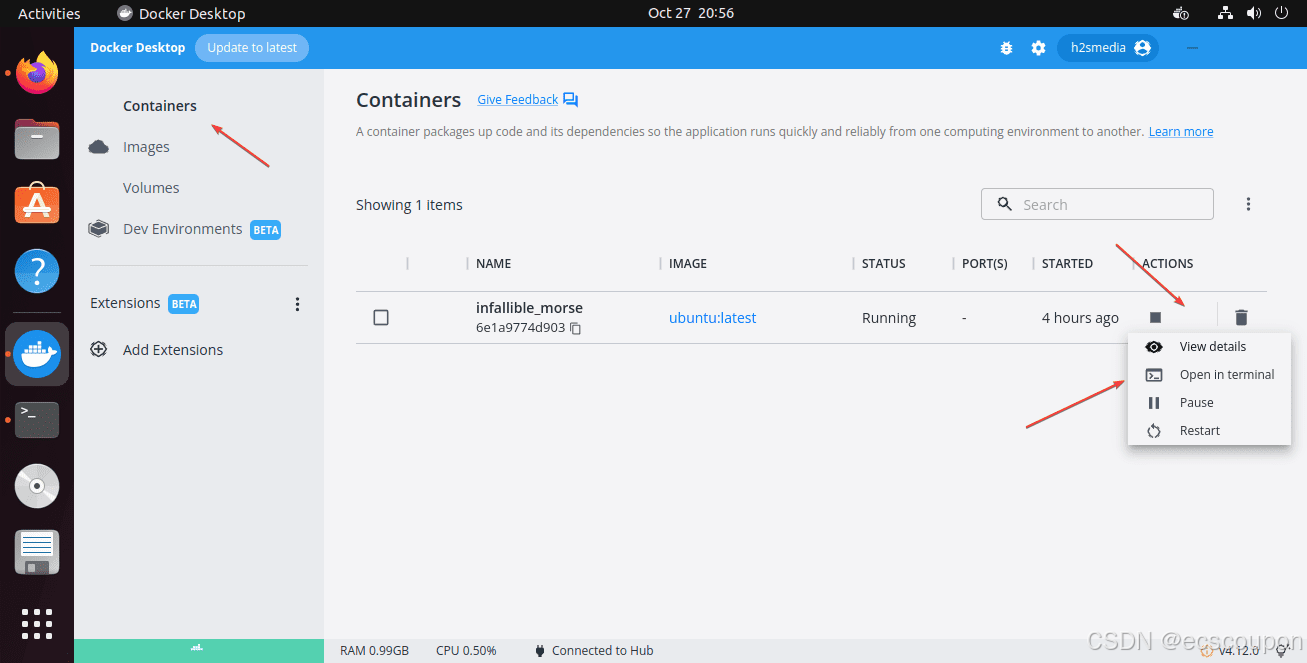
Ubuntu 24.04 LTS Noble安装Docker Desktop简单教程
Docker 为用户提供了在 Ubuntu Linux 上快速创建虚拟容器的能力。但是,那些不想使用命令行管理容器的人可以在 Ubuntu 24.04 LTS 上安装 Docker Desktop GUI,本教程将提供用于设置 Docker 图形用户界面的命令…… Docker Desktop 是一个易于使用的集成容…...

XML 和 SimpleXML 入门教程
XML 和 SimpleXML 入门教程 XML(可扩展标记语言)是一种用于存储和传输数据的标记语言。它是一种自我描述的语言,允许用户定义自己的标签来表示数据。SimpleXML 是 PHP 中的一个扩展,用于解析和操作 XML 数据。本文将介绍 XML 和 …...

leetcode--链表类题目总结
本文作为刷题时对链表类题目的总结. 常见技巧: 引入虚拟头节点 便于处理边界情况便于对链表操作快慢双指针(判环,找环的入口等)链表逆序(推荐使用 虚拟头节点 头插法 进行逆序) 链表逆序( 头插法 虚拟头节点):链表内指定区间反转_牛客题霸_牛客网 虚拟节点:合并…...

打卡第22天------回溯算法
开始学习了,希望我可以尽快成功上岸! 一、回溯理论基础 什么是回溯法?回溯法也可以叫做回溯搜索法,它是一种搜索的方式。 回溯是递归的副产品,只要有递归就会有回溯。 回溯法的效率回溯法的本质是穷举,穷举所有可能,然后找出我们想要的答案。如果想让回溯法高效一些,可…...

Ubuntu对比两个文件内容有什么区别?
在Ubuntu(或任何基于Linux的系统)中,你可以使用多种命令行工具来比较两个文件的内容差异。以下是一些常用的方法: 1. **diff 命令**: diff 是Linux中用于比较两个文件差异的标准工具。它逐行比较文件,并显示…...

python:本机摄像头目标检测实时推理(使用YOLOv8n模型)
本文将介绍如何使用本机摄像头进行目标检测实时推理的python代码。 文章目录 一、下载YOLO权重文件二、环境配置三、完整代码 一、下载YOLO权重文件 https://github.com/ultralytics/ultralytics?tabreadme-ov-file 拉到网页最下面,选择适合的模型,下…...

Spark实时(四):Strctured Streaming简单应用
文章目录 Strctured Streaming简单应用 一、Output Modes输出模式 二、Streaming Table API 三、Triggers 1、unspecified(默认模式) 2、Fixed interval micro-batches&am…...

SpringBoot上传超大文件导致OOM,完美问题解决办法
问题描述 报错: Caused by: java.lang.OutOfMemoryError at java.io.ByteArrayOutputStream.hugeCapacity(ByteArrayOutputStream.java:123) ~[?:1.8.0_381] at java.io.ByteArrayOutputStream.grow(ByteArrayOutputStream.java:117) ~[?:1.8.0_381] at java.…...

PyTorch 的各个核心模块和它们的功能
1. torch 核心功能 张量操作:PyTorch 的张量是一个多维数组,类似于 NumPy 的 ndarray,但支持 GPU 加速。数学运算:提供了各种数学运算,包括线性代数操作、随机数生成等。自动微分:torch.autograd 模块用于…...

Java开发之LinkedList源码分析
#来自ゾフィー(佐菲) 1 简介 LinkedList 的底层数据结构是双向链表。可以当作链表、栈、队列、双端队列来使用。有以下特点: 在插入或删除数据时,性能好;允许有 null 值;查询效率不高;线程不安…...

外卖霸王餐系统架构怎么选?
在当今日益繁荣的外卖市场中,外卖霸王餐作为一种独特的营销策略,受到了众多商家的青睐。然而,要想成功实施外卖霸王餐活动,一个安全、稳定且高效的架构选择至关重要。本文将深入探讨外卖霸王餐架构的选择,以期为商家提…...

AV1技术学习:Transform Coding
对预测残差进行变换编码,去除潜在的空间相关性。VP9 采用统一的变换块大小设计,编码块中的所有的块共享相同的变换大小。VP9 支持 4 4、8 8、16 16、32 32 四种正方形变换大小。根据预测模式选择由一维离散余弦变换 (DCT) 和非对称离散正弦变换 (ADS…...

Git操作指令
Git操作指令 一、安装git 1、设置配置信息: # global全局配置 git config --global user.name "Your username" git config --global user.email "Your email"2、查看git版本号 git -v # or git --version3、查看配置信息: git…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

